帶加強圈外壓薄壁圓柱殼體穩定性有限元分析

朱振華，崔偉，鄭祥凱

（長春理工大學 機電工程學院，長春 130022）

帶加強圈外壓薄壁圓柱殼體穩定性有限元分析

朱振華，崔偉，鄭祥凱

（長春理工大學 機電工程學院，長春 130022）

殼體在承受外壓的作用時，往往因穩定性不足導致殼體的變形或者壓扁，為避免殼體變形，通常在殼體外表面或內表面設置加強圈，以增加殼體的穩定性。采用有限元分析軟件ANSYS對有無加強圈的薄壁圓柱殼體進行特征值屈曲分析，探究外加強圈對圓柱殼體的影響。同時針對含有不等高度、不等加強圈厚度以及不等加強圈的間距的薄壁圓柱殼體進行穩定性分析，以便以后能夠設計出更加合理的加強圈滿足穩定性的要求。

薄壁圓柱殼體；穩定性；加強圈；臨界壓力

外壓殼體的失穩是指當殼體受外壓作用時，外壓載荷增大到某一值時，殼體會突然失去原有的形狀，被壓癟或產生波紋，當載荷卸去后，殼體仍不能恢復原來的形狀［1］。為避免殼體失穩變形，通常在殼體外表面或內表面設置加強圈，以增加殼體的穩定性。

目前有限元分析軟件ANSYS在工程上運用比較廣泛，它提供了兩種分析方法，特征值屈曲分析和非線性屈曲分析（幾何非線性、材料非線性）［2］。現主要采用有限元分析軟件ANSYS提供的特征值屈曲分析方法對有無加強圈的外壓薄壁圓柱殼體進行分析，并且利用該有限元軟件提供的方法對含有不同尺寸的加強圈的圓柱殼體進行穩定性分析，探究外加強圈的尺寸對薄壁圓柱殼體失穩產生何種影響。圓柱殼分為長圓筒、短圓筒、剛性圓筒，因長圓筒失穩時出現的波紋數為2，相對于短圓筒失穩時波紋數為大于2［3］，短圓筒失穩變形比較復雜，長圓筒失穩變形比較簡單，因此現只探討短圓筒的穩定性問題。

1 無加強圈的圓柱殼體有限元分析

1.1 特征值屈曲分析

特征值屈曲分析屬于結構線性分析，分析簡單，計算速度快。該方法不考慮初始缺陷如初始變形和應力狀態，不考慮材料的非線性，雖然特征值屈曲分析經常得出非保守的結果，但還是比較接近理論計算結果的，在實際工程中運用還是比較多的［4，5］。

求解過程如圖1所示：

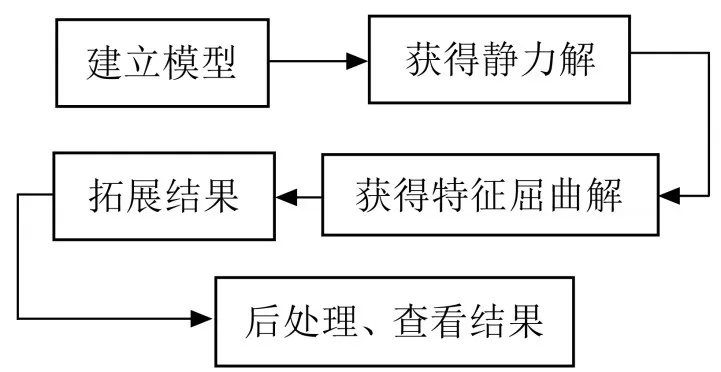
圖1 特征值屈曲分析流程圖

1.2 對無加強圈薄壁圓柱殼體進行分析

對于受均布外壓薄壁圓柱殼體，取材質為16MnR，內徑為Do=1500mm，長度L=3000mm，壁厚t=18mm的圓柱殼體。筒體采用有限元ANSYS軟件提供的Shell181殼體單元［6］，該單元非常適用于線性分析，殼體的厚度變化是為了適應非線性分析。約束筒體兩端的非軸向位移，其中一端同時約束軸向位移［7］。其彈性模量E=210GMPa，泊松比μ=0.3。對其進行特征值屈曲分析得到的結果：4.756MPa，得到薄壁圓柱殼體失穩變形圖，如圖2所示。

圖2 筒體失穩變形圖

從圖2（a）中的筒體截面圖可以看出，該筒體失穩時的波形數為4，這與理論公式計算得到的波形數相一致，該方法分析出的結果還是比較準確的。從（b）圖中可以觀察到筒體因穩定性不足，在外壓的作用下，出現明顯的壓邉變形。

1.3 帶加強圈的圓柱殼體有限元分析

從短圓筒的臨界失穩公式可知，減小圓筒的長度L或增加筒體的壁厚t，都可以提高外壓圓筒的失穩臨界壓力Pcr，而減小L的方法是在筒體外部或內部設置加強圈［8，9］。因內外加強圈的加強原理類似，且外加強圈在實際工程上運用比較多，所以現只討論外加強圈對殼體的加強效果。加強圈的型式很多，比如T型、扁型、半圓環殼、II型等，現主要對扁型加強圈的圓柱殼體進行穩定性分析［10］，圖3為帶加強圈的薄壁圓柱殼體。

圖3 帶加強圈的薄壁圓柱殼體

加強圈與殼體可以采用連續焊接或間斷焊接，有時也采用鉚接，但不論采用何種焊接，必須保證其強度，不能任意削弱或割斷。在殼體外部設置加強圈若采用間斷焊接，其間斷焊每側焊縫的總長度不應小于殼體外圓周長的1/2。間斷焊縫可以相互錯開或者并排排列，其焊縫與筒體的連接如圖4所示，對設置外加強圈，最大間距t=8δn（筒體的名義厚度）。

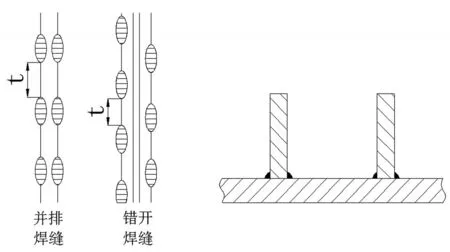
圖4 焊縫與筒體連接

筒體受均布外壓作用下的受力圖如圖5所示，設有無加強圈的筒體受到相同的外壓，研究其外加強圈對筒體的影響。

表1 有無加強圈的圓筒失穩臨界壓力

圖5 有無加強圈筒體受力圖

加強圈和筒體均采用ANSYS提供Shell181單元類型，彈性模量E=210GMPa，泊松比μ=0.3，取筒體長度為L=6000mm，內徑為D=1000mm，壁厚為t=10mm，加強圈的壁厚為b=20mm，加強圈的高度h=80mm，對其進行特征值屈曲分析得到的結果：4.057MPa。圖6為帶加強圈的圓柱殼體失穩變形圖。

圖6 帶加強圈筒體失穩變形圖

從圖6帶加強圈的筒體失穩變形圖中的（a）、（b）可知，筒體在外壓的作用下，出現明顯的整體失穩。帶加強圈的圓柱殼體在外壓的作用下會出現兩種失穩形式，加強圈段內的筒體失穩破壞和圓柱殼體整體失穩破壞，關于整體失穩和筒間的失穩也有學者研究［11］，這里不再討論。

為了探討加強圈對筒體的加強效果，加強圈和薄壁筒體都采用ANSYS提供的Shell181單元類型，彈性模量E=210GMPa，泊松比μ=0.3。利用特征值屈曲分析確定臨界失穩的壓力，加強圈的壁厚、高度以及加強圈的間距取合理的數值［12］，得到表1臨界失穩壓力。

從表1數據可知帶外加強圈的薄壁圓柱殼體失穩時的臨界壓力遠遠大于無加強圈的圓柱殼體，約是無加強圈的2.5倍。這說明筒體設置加強圈能較好地提高筒體失穩時的臨界壓力，提高筒體的穩定性，減少因穩定性不足導致筒體的失穩破壞，因此必要時，設置加強圈是非常有必要的。

2 不同尺寸的加強圈對薄壁筒體的影響

2.1 不同高度h對薄壁筒體的影響

從上述分析結果可知設置加強圈的確可以大大提高薄壁筒體失穩時的臨界壓力，但是不同尺寸的加強圈對筒體的穩定性有何影響。雖然有些學者給出了設計加強圈尺寸理論計算［13］，但是有時并不滿足工程的實際需求，因此探究計算不同加強圈的壁厚b、不同高度h、以及不等加強圈間距Ls對薄壁筒體的影響是非常重要的。同樣，加強圈和筒體均采用ANSYS提供Shell181單元類型，彈性模量E=210GMPa，泊松比μ=0.3，取筒體長度為L=6000mm，內徑為D=1000mm，壁厚為t=10mm，加強圈的壁厚為b=20mm，對不同尺寸h值進行特征值屈曲分析，表2為不同高度h對應失穩時的臨界壓力，根據表2數據繪制失穩臨界壓力曲線圖，如圖7所示。

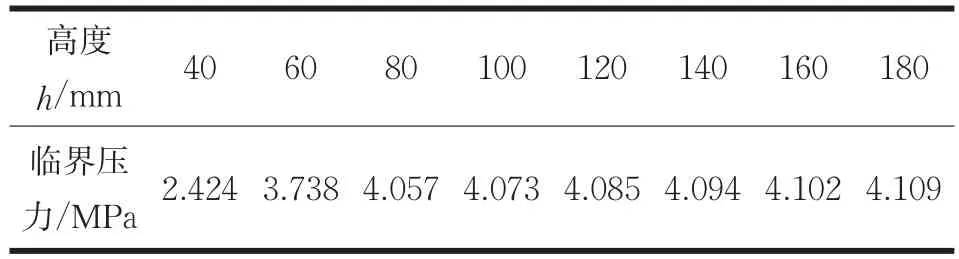
表2 不同高度h失穩時臨界壓力

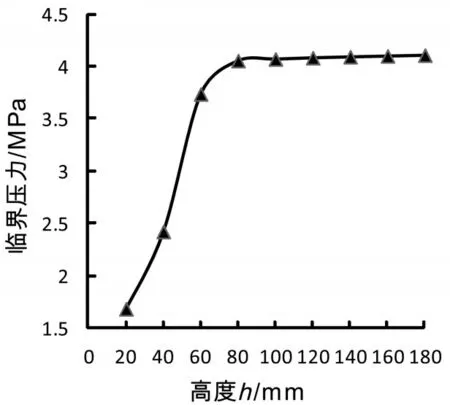
圖7 不同加強圈高度h對應的臨界壓力

從圖7可知隨著加強圈高度h的增加，失穩時臨界壓力Pcr也隨之增大，曲線上升的趨勢比較顯著。但增到一定的數值后，曲線逐漸趨于平緩，臨界壓力Pcr接近于定值。這說明在一定的高度范圍內，增加加強圈的高度可以有效提高臨界壓力，但超過此范圍增加高度對提高臨界壓力不明顯。多數學者在對帶加強圈的殼體進行穩定性分析時，也得出類似的結論。因此，在設計加強圈的高度時取合理的數值還是比較重要的，取值過高造成材料的浪費，取值過低起不到加強的效果。

2.2 不同壁厚b對薄壁筒體的影響

為探究不同壁厚b對筒體的影響，加強圈和筒體均采用ANSYS提供Shell181單元類型，彈性模量E=210GMPa，泊松比μ=0.3，取筒體長度為L=6000mm，內徑為D=1000mm，壁厚為t=10mm，加強圈的高度h=80mm，取不同尺寸的加強圈壁厚b，對其進行特征值屈曲分析。得到表3對應的失穩時臨界壓力，根據表3數據繪制圖8失穩臨界壓力曲線圖。

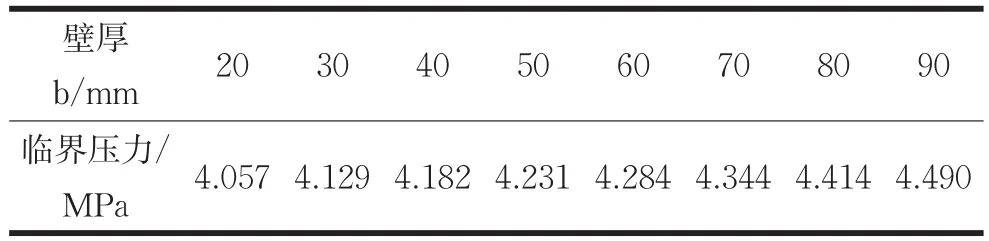
表3 不同壁厚b失穩時臨界壓力

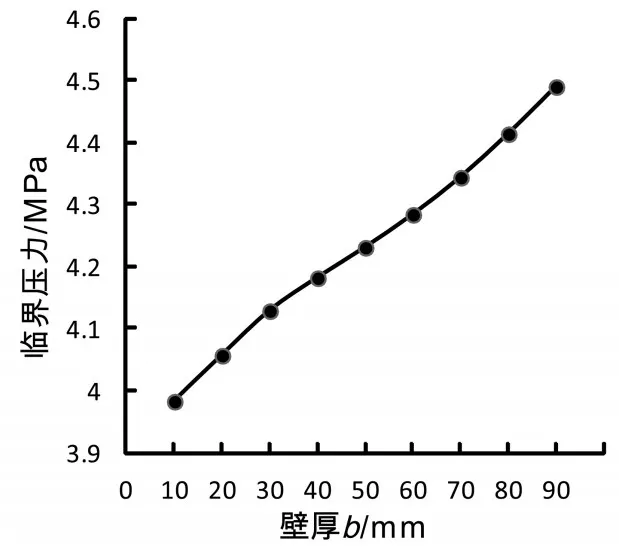
圖8 不同加強圈壁厚b對應的臨界壓力

從圖8可知隨著加強圈壁厚b的增加，失穩時臨近壓力也隨之增大，曲線呈上升的曲線，但是從數值可以看出壁厚b從10mm到90mm，臨界壓力才增加約0.5MPa，增量不是很顯著，這與加強圈的理論結果相一致。這說明增加加強圈的壁厚確實可以提高失穩時的臨界壓力，但是提高的幅度不是很顯著。因此，在設計加強圈的壁厚時應該取合理的數據。

2.3 不等加強圈間距對薄壁筒體的影響

為探究加強圈間距對薄壁筒體的影響，則加強圈和筒體均采用ANSYS提供Shell181單元類型，彈性模量E=210GMPa，泊松比μ=0.3，取筒體長度為L=6000mm，內徑為D=1000mm，壁厚為t=10mm，加強圈的壁厚b=20mm，加強圈的高度h=80mm，取不同加強圈的間距Ls，對其進行特征值屈曲分析。得到表4對應的失穩時臨界壓力，根據表4數據繪制圖8失穩臨界壓力曲線圖。

表4 不同間距Ls失穩臨界壓力

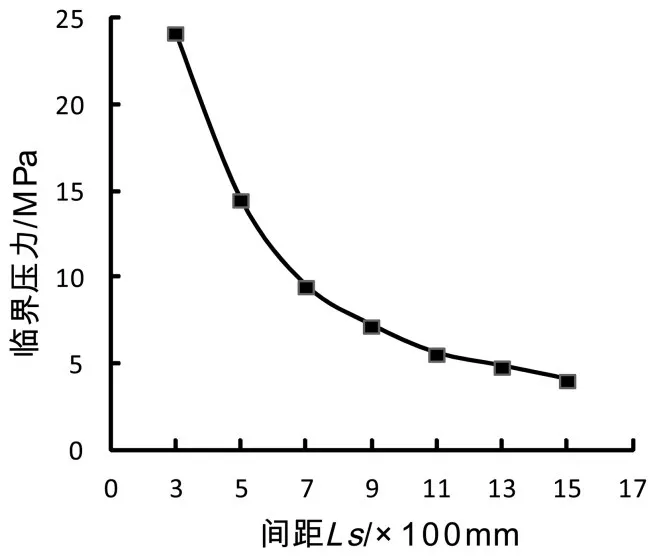
圖9 不同間距Ls對應的臨界壓力

從圖9可知隨著加強圈間距Ls的增大，失穩時臨界壓力Pcr減小，曲線圖下降的趨勢比較顯著。這說明減小加強圈的間距，即增加加強圈的個數可以明顯地提高失穩時的臨界壓力。因此選擇合理的加強圈的間距很重要，間距過短造成材料的浪費，間距過長起不到加強的效果。

3 結論

從上述對薄壁圓柱殼體采用有限元分析方法進行特征值屈曲分析，并且探究不同尺寸外加強圈對圓柱殼體的影響，可以得出如下結論：（1）對薄壁圓柱殼體設置合理的加強圈可以很好地提高臨界壓力，避免因穩定性不足導致的失穩破壞，因此合理的設置加強圈很重要。

（2）對于不同尺寸外加強圈的圓柱殼體采用特征值屈曲分析，可知加強圈的高度、壁厚以及加強圈的間距對筒體的影響不同。在一定范圍內，隨加強圈高度的增加，臨界壓力增大，但到增到一定的數值時，臨界壓力趨于定值。隨加強圈的壁厚增加，臨界壓力增大，但是增大的幅度不明顯。隨加強圈間距的減小，臨界壓力增大。但是在實際中設計過程中，還是要取合理的數值，取值過大或過小都會造成材料的浪費或滿足不了穩定性的要求，因此設計更為合理的加強圈的尺寸還要根據具體情況具體分析。

［1］鄭津洋，董其伍，桑芝富.過程設備設計（第二版）［M］.北京：化學工業出版社，2011：68-76.

［2］余軍昌，徐超，張峰，等.基于ANSYS的外壓圓柱殼的屈曲分析［J］.輕工機械，2013，31（1）：29-31.

［3］張吳星.外壓薄壁短圓筒臨界失穩壓力理論及試驗研究［J］.湘潭大學自然科學學報，2001，23（2）：81-83.

［4］Najafizadeh M M ，Hasani A，Khazaeinejad P.Mechanical stability of functionally graded stiffened cylindrical shells［J］.Applied Mathematical Modelling，2009，33（2）：1151-1157.

［5］Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression Nonlinear finite element method investigations［J］.Ocean Engineering，2009，36（3/4）：266-267.

［6］余偉煒，高炳軍.ANSYS在機械與化工設備中的應用（第二版）［M］.北京：中國水利水電出版社，2007：84-97.

［7］朱艷，王傳志，董俊華，等，外壓薄壁圓筒弱強結構及其臨界壓力的計算［J］.機械強度，2016，38（4）：811-815.

［8］李志義，喻健良，劉志軍.過程機械［M］.北京：化學工業出版社，2008：73-77.

［9］童長河，劉康林，孫太平，等，帶加強圈外壓柱殼的穩定性分析［J］.石油化工設備，2012，41（5）：28-32.

［10］田琳靜，董俊華，高炳軍.螺旋加強圈加強外壓圓筒穩定性研究［J］.機械強度，2014，36（4）：566-517.

［11］楊德慶，羅放，陳靜.有限元功率流落差計算方法研究［J］.噪聲與振動控制，2009（6）：127-131.

［12］聶修民.過程裝備與控制工程綜合實驗系統設計與研究［D］.長春：長春理工大學，2012

［13］宋明晨，金志浩.外壓圓筒加強圈設計［J］.石油化工設備技術，1991，12（5）：2-11

Finite Element Analysis of Ring-stiffened Thin-walled Cylindrical Shells Subjected to External Pressure Stability

ZHU Zhenhua，CUI Wei，ZHENG Xiangkai
（School of Mechatronic Engineering，Changchun University of Science and Technology，Changchun 130022）

When the shell receives external forces，the shell often is deformed or flattened because of lack of stability.To avoid shell deformation，usually the ring-stiffening is set in the shell outer surface or inner surface in order to increase the stability of the shell.Eigenvalue buckling analysis of thin-walled cylindrical shells with or without stiffening rings are carried out by finite element analytic software named ANSYS.The influence of outer stiffening ring on the cylindrical shells is o investigated.At the same time，the stability analysis of thin-walled cylindrical shells with unequal height，unequal thickness and unequal spacing is carried out.In order to design a more reasonable reinforcing ring，the stability requirements can be satisfied.

thin-walled cylindrical shell；stability；stiffening ring；buckling pressure

TQ320.725

A

1672-9870（2017）04-0049-04

2017-03-02

朱振華（1970-），男，碩士，副教授，E-mail：zhuzhenhua0431@163.com