小當量地下爆炸的質點速度模型*

李學政,王敏超

(西北核技術研究所，陜西 西安 710024)

小當量地下爆炸的質點速度模型*

李學政,王敏超

(西北核技術研究所，陜西 西安 710024)

在第四紀砂礫層中進行了系列公斤至百公斤級的地下封閉爆炸，研究了小當量化學爆炸地震波傳播規律。在近場，地震波持時很短，水平振幅強于垂向振幅。質點速度隨當量呈現指數增加，水平向指數為1.09，垂直向指數為0.77，質點速度隨距離呈現指數衰減，水平向和垂直向指數分別為2.07與1.57。Sadauskas模型、顯函模型和雙極模型都能定量描述小當量地下爆炸地震波質點速度變化，但他們之間的反演精度存在差異，雙極模型的殘差最小。換言之，采用雙極模型反演的數據更接近實際。

雙極模型;地下爆炸;第四紀砂礫層;地震波質點速度

地下爆炸廣泛應用于工業、農業和國防等領域。因此，有關地下介質的爆破破碎機理、爆炸波數值模擬、地震波傳播特征和地震效應等，已經進行了大量研究[1-10]。尤其是地下爆炸發生的地震效應,雖然爆炸地震和天然地震的形成機理存在很大差別，但是他們都激發地震波，引起地震動，對地表和人類工程建筑物造成破壞，在某種程度上，破壞效果是類似的。而造成地震破壞效應的強弱主要取決于爆炸激發的地震波引起的地介質質點運動參數大小。因此，有關地下爆炸引起的地震波傳播規律、介質質點運動參數計算方法，一直備受關注。

本文中，基于第四紀砂礫層中小當量(即當量在公斤級至百公斤級范圍)的封閉爆炸的觀測資料，針對波形中優勢橫波進行分析處理，分析爆炸地震波水平與垂向質點速度隨當量和距離變化，并對幾種模型在描述觀測數據方面的殘差進行分析對比，確定描述第四紀砂礫層介質的地震波質點運動速度模型。

1 數學模型

介質的質點運動參數與爆炸當量、方式、源區介質和觀測距離等眾多因素有關。一般地,爆炸當量越大,激發的地震波就越強,爆炸封閉越好,爆炸能量耦合到介質中能量越高。爆炸能量耦合到介質中的比例(即能量耦合系數)主要和爆炸方式及爆炸所處的介質等因素有關。學者建立數學模型時，對地下封閉爆炸和拋灑爆炸、巖石與土層分別研究，從而大大簡化了模型，使數學模型更有實用性[5]。歸結起來，現有模型主要有以下幾種。

(1)Sadauskas模型。Sadauskas模型[5]的地下爆炸質點速度為：

(1)

式中：質點速度v的單位為cm/s，當量W的單位為kg，距離R的單位為m。對于巖石，K=50，對于土壤，K=200，α=1～2。

(2)顯函模型。謝毓壽等[10]基于炸藥量為0.05～2.0 kg TNT、距離在35～404 m范圍內的數據，確定了振動質點速度為：

lgv=K0+αlgW+βlgR

上式可改寫為：

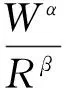
(2)

式中：K=10K0，對于堅硬巖石，K0=2.2～2.6，α=0.60，β=1.80。

雙極模型。用Sadauskas模型參數計算時，先計算比例距離，并且規定恒定的指數。而用顯函模型計算α、β時，要基于較多樣本參量，且需要各次爆炸空間位置不變等條件，否則將帶來一定數據誤差。為解決這個問題，雙極模型[6]被提了出來。該模型在計算模型參數時不同于傳統的上述兩個模型計算方法，而是在一定當量指數變化區間內，查找最合適參數，使模型預測數據和實測數據具有更高的一致性。質點速度為：

(3)

式中：對于黃土層，K為0.40，α為2.0，β為2.3。

2 實驗與檢測

2.1場地介質

野外爆炸實驗場地相當開闊,地形沒有明顯起伏，地面十分平坦。整個場地未見堅硬基巖，出露的地層為第四紀沖積層，為砂礫石混合體，礫石大小不一，多數礫石呈現長橢球和不規則形狀，具有較低的磨圓度和篩選度。在地表以下至6 m之間，砂礫層中含砂比例較高,6 m以下直至20 m深處, 砂礫層中含砂比例明顯降低。實驗場地構造相對簡單，未發育大的斷裂構造。砂礫石混合體結構十分松散，地表僅被一些植物稀疏覆蓋，宏觀上為一片植被不甚發育的荒漠區域。

2.2檢測儀器與布設

所用的檢測地震波儀器是短周期型LE-3Dlite，機電換能靈敏度為400V/(m·s-1), 檢波器噪聲很低，能夠檢測1～80 Hz范圍內的振動信號。該地震檢波儀器為三分向組合體，可以在三維方向檢測地震波質點振動幅值。

地表出露的為第四紀砂礫層，地勢比較平坦。在爆炸點周圍不同方向，距離在0.5～5 km范圍內，布設了十幾個地震波檢測點，爆炸源與檢測點分布如圖1所示。

系列爆炸源主要為20、100和300 kg的TNT炸藥，從地表向下開挖約20 m深井，將炸藥放在井底部，然后用挖出來的砂礫石進行回填，增強爆炸能量耦合，提高彈性能在爆炸能量中的比例。

3 測量結果

3.1測量概況

為確定本底噪聲，在E1臺站記錄信號前截取了20s的數據。其本底波形比較穩定，振幅大約為0.5 μm/s，傅立葉振幅從低頻到高頻漸漸降低，最大傅立葉振幅為零頻極限值，優勢頻帶主要限制在3 Hz以下。針對這次實驗布設十幾個觀測點，均記錄到了良好的數據。地震波形持時很短，僅為數秒鐘，兩個水平方向的地震波形，在振動幅值大小、包絡線形態和波形持時方面具有較好的一致性，而垂向和水平向波形在上述幾方面明顯不同，波形振幅遠強于水平向振幅。隨著距離增大，波形復雜性明顯增加，如圖2所示。

3.2質點運動速度

實驗所用的LE-3Dlite地震計，能夠測量東西、南北和垂向3個方向的地運動數據，通過靈敏度換算，可以直接得出地運動質點速度ve、vn、vv。表1為爆炸當量為300 kg爆炸實驗部分觀測點質點速度。根據表1，質點水平速度ve與南北速度vn互有大小，ven為水平均值，均大于垂直速度。統計上ve大于vn，垂向vv小于任意水平上幅值。數據表明，爆炸激發的地震波，水平上振幅強于垂向振幅。

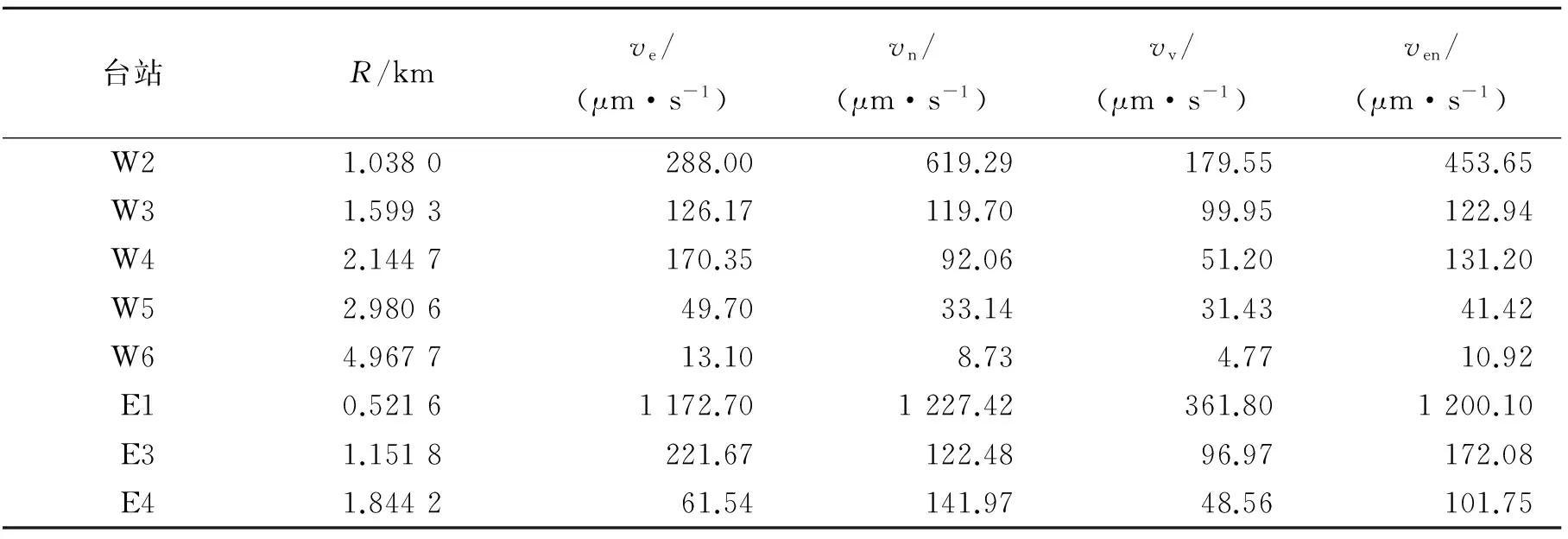
表1 300 kg實驗部分觀測點質點速度Table 1 Partial observation data of 300 kg explosion

4 模型確定

4.1Sadauskas模型

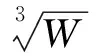
(4)

4.2顯函模型

式(2)是距離R、W的二元函數，該式反映了地介質質點速度隨距離增加而衰減、隨當量增長而增長的關系，隨距離的衰減指數可以通過一次實驗不同距離的檢測點速度計算確定，而隨當量的指數可以通過同一觀測點不同當量的實驗數據得出。 由于地下介質的復雜性，存在介質能量吸收和球面擴散作用，地震波在傳播過程中，能量逐漸消耗，地震波幅值隨著距離增加發生衰減，不同介質中衰減指數是不同的。本文中采用最小二乘法，對地震波的水平和垂直數據進行了回歸計算，其計算結果如圖4所示。

圖4(a)為質點水平速度與距離的擬合曲線。圖中3種不同當量爆炸的擬合曲線大致是平行的，距離指數為-2.07，相關系數為0.97。 圖4(c)為質點垂直速度與距離擬合曲線, 距離指數為-1.57，相關系數為0.99。二者相比，質點垂直速度相比于水平速度，與距離的相關性更強。圖4(b)為質點水平速度與當量擬和曲線。圖為20～300 的4次爆炸，在0.51、1.03和4.99 km的距離測點上的數據擬和曲線，這幾條曲線大致是平行，但存在一定差別，當量指數約為1.09，相關系數為0.99。 圖4(d)為質點垂直速度與當量擬合曲線, 當量指數為0.77，相關系數為0.97。于是顯函模型為：

(5)

4.3雙極模型

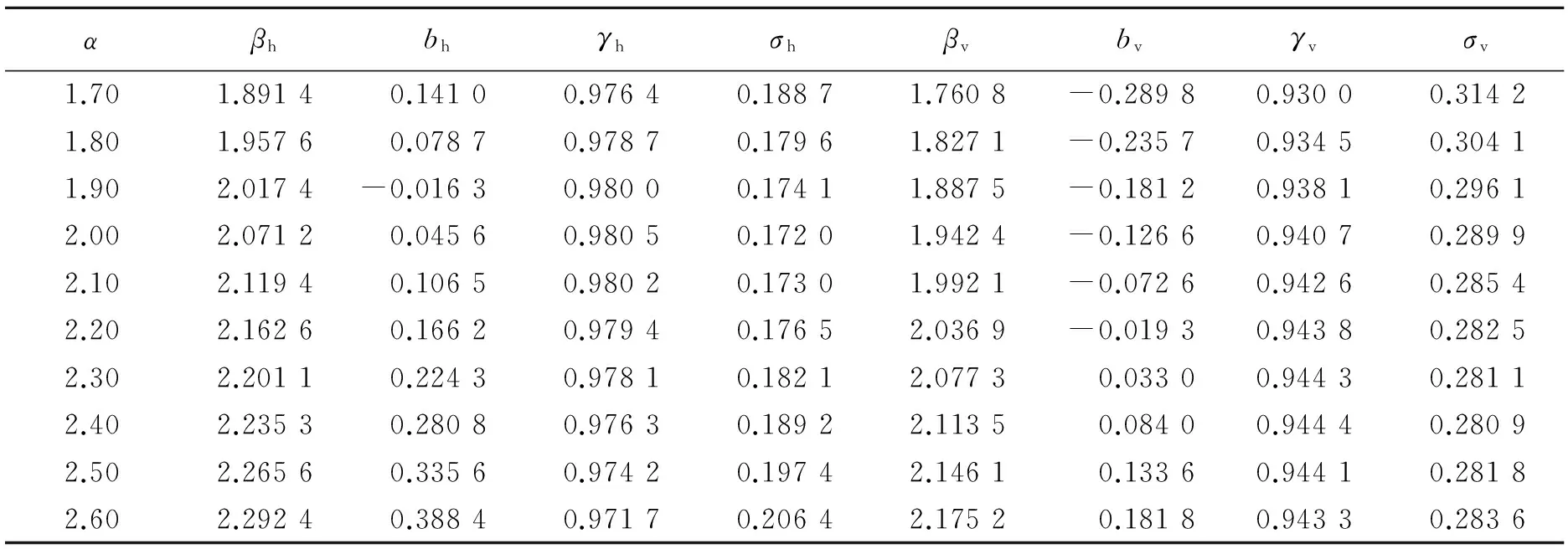
由于爆炸激發的質點振動參數和爆炸當量正相關，隨著當量增大而增大，且呈顯出指數增長關系。雙極模型參數測定完全不同于傳統的Sadauskas模型和顯函模型模型測定方法，采用區間尋優方法，確定最佳的當量指數[4]。具體計算時，首先，給定一個當量指數，計算與距離的比值，利用最小二乘法進行回歸計算，得出模型參數，采用模型反演質點速度數據，并和實測數據進行對比，確定實測和反演數據之間的殘差值。然后,用一定的步長，選擇下一個當量指數，計算殘差，步長越小，計算的結果越細致，但計算量也越大。將選定的區間內所有點計算完畢，從所有計算殘差列表中選取最小殘差所對應的參數，即為速度模型參數。本文中在1.0至2.5之間采用0.05步長進行計算，部分計算結果見表2，如圖5所示。α、β、b、γ和σ分別表示當量開方次數、比例距離指數、回歸截距、相關系數和殘差。

根據表2，水平向在當量指數1.7至2.0區間內，反演與實測數據之間的殘差，從開始的逐漸減小，到2.0時達到極小值，為0.172，從2.0到2.6之間又逐漸回升增大。整個曲線為凹向上形態，如圖5(a)所示 。而相關系數在在2.0達到極大值，相關性最強。垂直向在當量指數2.4時，同時達到殘差最小和相關系數最大。殘差變化如圖5(b)所示。圖5(c)～(d)為水平與垂直向質點速度擬合曲線。雙極模型為：

(6)

αβhbhγhσhβvbvγvσv1.701.89140.14100.97640.18871.7608-0.28980.93000.31421.801.95760.07870.97870.17961.8271-0.23570.93450.30411.902.0174-0.01630.98000.17411.8875-0.18120.93810.29612.002.07120.04560.98050.17201.9424-0.12660.94070.28992.102.11940.10650.98020.17301.9921-0.07260.94260.28542.202.16260.16620.97940.17652.0369-0.01930.94380.28252.302.20110.22430.97810.18212.07730.03300.94430.28112.402.23530.28080.97630.18922.11350.08400.94440.28092.502.26560.33560.97420.19742.14610.13360.94410.28182.602.29240.38840.97170.20642.17520.18180.94330.2836

5 模型分析

顯函模型中，采用固定系列爆炸位置，確定質點速度隨當量增大指數。事實上，爆炸位置盡管變化不大，但每次的地下爆炸不能完全重復，各爆炸位置之間依然有數十米的距離。嚴格來講，位置不變，工程上是難以實現。因此當量指數測定存在一定誤差。水平質點速度的當量指數具有一定分散性，均值為1.09、20～300 kg的質點速度隨距離的衰減指數，一致性比較好，均值為-2.07。垂直向質點速度的當量指數為0.77、20～300 kg的質點速度隨距離的衰減指數在-1.55至-1.58之間，均值為1.57。距離衰減指數相對于當量增長指數，精度要高得多。

雙極模型中，水平與垂直向質點速度當量的指數分別是1/2.0和1/2.4，其殘差分別0.172和0.280。而Sadauskas模型的水平與垂直向速度的殘差分別為0.245和0.297，顯函模型的水平與垂直向速度的殘差分別為0.171和0.300。雙極模型與Sadauskas模型和顯函模型相比，在反演或預測質點速度參數方面，更加接近實際數據。

6 結 論

在第四紀砂礫介質中進行了公斤至百公斤級系列地下封閉爆炸，通過對0.5～5.0 km范圍地震波測量和數據分析，得出如下結論。

地震波水平振幅強于垂向振幅,質點速度隨當量呈現指數增加，水平指數為1.09，垂直指數為0.77，質點速度隨距離呈現指數衰減，水平指數為2.07，垂直指數為1.57。Sadauskas模型、顯函模型和雙極模型都能夠描述小當量地下爆炸地震波質點速度。反演計算結果顯示，雙極模型的殘差最小，顯函模型次之，Sadauskas模型最大。換言之，采用雙極模型反演的數據更加接近實際。

[1] 劉愛文,俞言祥,付長華,等.50 t科學爆破振動的衰減特征及地形效應[J].爆炸與沖擊,2010,30(1):21-26.

Liu Aiwei, Yu Yanxiang, Fu Changhua, et al. Attenuation characteristics and topographic effect of a scientif ic explosion with 50 t explosive[J]. Explosion and Shock Waves, 2010,30(1):21-26.

[2] 趙愛華,郭永霞,孫為國,等.華北地區礦山爆破活動的時空特征[J].地球物理學進展,2012,27(3):917-923.

Zhao Aihua, Guo Yongxia, Sun Weiguo, et al. Spatio-temporal characteristics of mine blast activity in North China[J]. Progress in Geophys, 2012,27(3):917-923.

[3] 崔汝國,王尚旭,寧鵬鵬,等.炸藥震源在濟陽坳陷粘土介質中的激發理論初探[J].石油物探,2009,48(6):601-610.

Cui Ruguo, Wang Shangxu, Ning Pengpeng, et al. Preliminary discussion on shooting theory for dynamite in clay medium of Jiyang[J]. Geophysical Prospecting for Petroleum, 2009,48(6):601-610.

[4] 陳亞娟,王利.土介質中TNT炸藥爆炸波傳播特性的數值模擬[J].河南理工大學學報(自然科學版),2010,29(1):88-91.

Chen Yajuan, Wang Li. Numerical study on the propagation and damage behavior of the blasing wave with TNT in soil medium[J]. Journal of Henan Polytechnic University (National Science), 2010,29(1):88-91.

[5] 張雪亮,黃樹棠.爆破地震效應[M].北京:地震出版社,1981.

[6] 李學政,張誠鎏,劉文學.封閉爆炸近場地震縱波及橫波質點速度模型[J].爆炸與沖擊,2011,31(2):196-203.

Li Xuezheng, Zhang Chengliu, Liu Wenxue. Particle velocity models of longitudinal and transversal waves in the near field of sealed explosions[J]. Explosion and Shock Waves, 2011,31(2):196-203.

[7] 林大超,張奇,白春華.爆炸地震效應的時頻分析[J].爆炸與沖擊,2003,23(1):32-36.

Lin Dachao, Zhang Qi, Bai Chunhua. Time frequency analysis of explosion seismic effects[J]. Explosion and Shock Waves, 2003,23(1):31-36.

[8] Bache C T. Estimating yield of underground nuclear explosion[J]. Bulletin of the Seismological Society of America, 1982,72(6):131-168.

[9] Khalturin V I, Rautian T G, Richards P G. The Seismic signal strength of chemical explosions[J]. Bulletin of the Seismological Society of America, 1998,88(6):1511-1524.

[10] 謝毓壽,王耀文.工業爆破的地震效應[J].地球物理學報,1962,11(2):154-161.

Xie Yushow, Wang Yaowen. Seismic effect of construction blasting[J]. Chinese Journal of Geophysics, 1962,11(2):154-163.

Abstract: A series of underground explosions whose yield is confined at a limited level ranging from a few kilograms to a hundred were carried out in the Quaternary Period hardpan. The law of seismic wave propagation on small yield chemical explosion was investigated in the experiments. The results show that the duration of the seismic waves were shorter in the near field, the horizontal vibration amplitudes was stronger than the perpendicular ones, and the particle velocity increases exponentially with the increase of the yield. An index in the horizontal direction was approximately 1.09, while that in the perpendicular direction was approximately 0.77. The particle velocity exponentially decreases with the increases of the distance. The attenuating index in the horizontal direction is 2.07 and that in the vertical direction is 1.57. It is shown that the Sadauskas model, the obvious model, and the double extreme model can all quantitatively describe the seismic particle velocity on small yield underground explosions but they differ in the inverse precision of the parameters. Here, the difference in the residual of the double extreme model is the least. In other words, the parameters inversed by using the double extreme model are closest to the data actually observed.

Keywords: double extreme model; underground explosion; Quaternary Period hardpan; seismic particle velocity

(責任編輯 丁 峰)

Particlevelocitymodelsonsmallyieldsundergroundexplosions

Li Xuezheng, Wang Minchao

(NorthwestInstituteofNuclearTechnology,Xi’an710024,Shaanxi,China)

O382.1國標學科代碼1303520

A

10.11883/1001-1455(2017)05-0899-07

2016-01-25；

2016-11-06

李學政(1957— )，男，博士，高級工程師,lixuzh@163.com。