黏塑性本構計算的穩定性分析*

劉明濤，李永池，胡秀章，章 杰

(1.中國工程物理研究院流體物理研究所,四川 綿陽 621999; 2.中國科學技術大學近代力學系,安徽 合肥 230027)

黏塑性本構計算的穩定性分析*

劉明濤1,2，李永池2，胡秀章2，章 杰2

(1.中國工程物理研究院流體物理研究所,四川 綿陽 621999; 2.中國科學技術大學近代力學系,安徽 合肥 230027)

提出本構方程計算方法的穩定性問題，針對黏塑性本構計算的顯式精確算法的穩定性進行分析，發現該算法并非無條件穩定，使用小擾動方法給出了其計算穩定的必要條件，穩定性條件對數值計算中的時間步長提出限制要求。通過有限元算例驗證了分析的正確性，計算結果也表明理論推導得到的穩定性公式能夠準確預測滿足計算穩定性條件要求的最大時間步長與各參數之間關系。

本構關系；算法穩定性；黏塑性本構；顯式精確算法

一直以來，塑性和黏塑性材料的本構方程及其數值算法的研究是計算力學的核心問題。D.C.Drucker等[1-2]提出了著名的Drucker公設，該公設是經典塑性理論的基石。利用Drucker公設可直接推導出塑性流動的正交法則和屈服面的外凸性，但其缺點是只適用于穩定材料。A.C.Palmer[3]指出針對軟化的非穩定材料也可以得到塑性流動的正交法則和屈服面的外凸性。李永池等[4]進一步發展了A.C.Palmer的思想，提出了廣義Drucker公設，將穩定材料和非穩定材料統一在一個框架之內。

Drucker公設推導出的塑性流動法則是塑性本構計算的基石，其指出塑性應變必須沿著當前加載面的法線方向發展。迄今為止，有關沖擊動力學問題的計算程序中，本構算法大部分采用傳統的半徑回歸法[5-7]，這是人們最初針對理想塑性材料提出的一種本構更新算法。對于具有應變率效應的黏塑性材料，采用這種算法會帶來較大的誤差，尤其是當材料由彈性狀態進入屈服狀態時。針對此問題，李永池等[8]提出了一種新的顯式本構計算方法，稱為顯式精確算法。基于廣義Drucker公設，李永池等[8]理論推導指出當黏塑性材料進入屈服狀態后，利用材料的實時狀態量即可唯一確定塑性流變過程中的塑性流動因子。若在一階精度下，利用上時刻的狀態量即可求出現時刻的塑性流動因子，繼而可計算現時刻的塑性變形，而后利用胡克定律可得現時刻的應力增量。

通常情況下，數值計算的穩定性是針對連續方程、動量方程和能量方程的差分格式而言。本文中探討本構方程計算方法的穩定性問題。對李永池等[8]發展的顯式精確算法進行穩定性分析，并通過對單個單元的有限元算例驗證其正確性。

1 顯式精確算法及其計算穩定性

顯式精確算法的詳細理論推導過程見文獻[8]，文獻[8]中是從一般性的熱黏塑性本構關系出發推導的，具有一定的普適性。本文中對其推導過程進行一定的簡化，從目前常見的Mises屈服準則下的黏塑性本構關系出發推導。

1.1顯式精確算法

針對Mises類黏塑性本構關系，屈服函數可設為：

(1)

其中，Mises等效應力和等效塑性應變率計算公式分別為：

(2)

(3)

根據廣義Drucker公設可知，塑性流動的正交法則為：

(4)

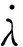
將式(1)～(2)代入式(4)得：

(5)

將式(5)代入式(3)，得：

(6)

由黏塑性本構方程式(1)，可反解出等效塑性應變率為：

(7)

式(6)、(7)聯立，得：

(8)

由式(8)可知，塑性流動因子可由材料當前的應力狀態唯一確定。

將式(8)代入式(5)得：

(9)

根據材料的胡克定律，有：

(10)

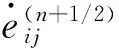
(11)

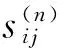
1.2計算穩定性分析

式(11)是一個張量表達式，不利于計算的穩定性分析。下面對此進行簡化，選擇一種特殊情況進行計算穩定性理論分析。

(12)

(13)

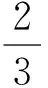
(14)

將式(12)～(14)代入式(11)，得：

(15)

由上式可計算得：

(16)

(17)

(18)

將函數g(s(n)+Δs)在s(n)處進行泰勒展開，可得：

g(s(n)+Δs(n))=g(s(n))+Δs(n)g′(s(n))+O(Δs(n)2)

(19)

將式(19)代入式(18)，并略去二階小量，得：

Δs(n+1)=Δs(n)[1-3Gdtg′(s(n))]

(20)

計算穩定性要求擾動的放大因子小于1，即|1-3Gdtg′(s(n))|<1，解得：

0<3Gdtg′(s(n))<2

(21)

式(21)即為推導得出的 顯式精確算法的計算穩定性條件，顯式精確算法的計算穩定性對計算時間步長dt提出了限制要求。還需特別指出的是，式(21)是在式(12)、(13)的特殊情況下推導得到的，并不能保證本構計算絕對穩定。

若選擇黏塑性材料的具體屈服準則形式為：

(22)

將式(22)代入式(21)，可得本構方程的計算穩定性要求為：

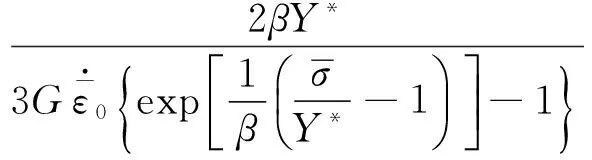
(23)

傳統Courant穩定性條件為：

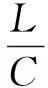
(24)

式中：L為單元特征長度，C為材料絕熱聲速，α為安全因數，通常取α=0.9。式(21)、(23)表明，本構計算的穩定性與材料的本構參數和實時塑性應變率密切相關，而傳統Courant穩定性條件僅與材料的聲速和單元的尺寸相關。

2 數值計算算例

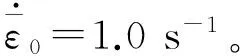
四邊形單元的運動過程設定為：在整個變形過程中4個節點在x方向均固定不動，同時節點1、2在y方向也固定不動，首先，節點3和4以速度-50 m/s沿著y方向勻速運動20 μs，四邊形單元的y方向長度由20 mm壓縮至19 mm；而后，節點3和節點4再以50 m/s勻速運動返回至初始位置，四邊形單元的y方向長度由19 mm回復至初始時的20 mm。

四邊形單元在上述變形過程中經歷的加卸載路徑較復雜，如圖1所示。從狀態1到狀態2，經歷了彈性加載、塑性加載；從狀態2到狀態3，經歷了彈性卸載、反向彈性加載、反向塑性加載，共5個階段。在第2階段和第5階段，材料發生了塑性應變，塑性應變率均約為1 700 s-1。根據顯式精確算法的穩定性條件式(2)，可知時間步長dt需滿足：0

2.1不同時間步長算例

2.1.1時間步長dt=0.3×10-7s時

計算結果如圖2所示，黑色實線為等效應力歷史曲線，藍色點劃線為等效塑性應變歷史曲線。從圖中可以看出，當選取的時間步長滿足計算穩定性條件式(23)時，利用顯式精確算法計算的結果能夠準確描述四邊形單元在整個變形過程中所經歷的復雜加卸載過程。

(1)彈性加載階段：隨著變形的增加，等效應力勻速增加，沒有發生塑性變形。

(2)塑性加載階段：由于節點3和節點4以勻速運動，因此在整個加載過程中等效塑性應變率保持不變，因此根據本構關系式(22)，等效應力也保持不變，而圖2中等效應力在該階段呈現1個平臺段，計算結果正確。

(3)彈性卸載階段： 20 μs以后，節點3和節點4沿原路徑勻速返回，材料進入彈性卸載階段，該過程中不產生塑性應變增量，因此等效塑性應變呈現平臺段，等效應力由材料的屈服點勻速降低至零，計算結果正確。

(4)反向彈性加載階段：當等效應力降低為零后，重新開始勻速增大，材料進入反向彈性加載階段，在此階段等效塑性應變不增大，呈現平臺段，計算結果正確。

(5)反向塑性加載：當材料由于反向加載再次進入屈服后，塑性變形重新開始累積，由于在該階段節點3和節點4勻速運動，因此塑性應變率保持為恒定值，所以塑性應變線性增大，等效應力出現第2個平臺段，計算結果正確。

2.1.2時間步長dt=1.0×10-7s時

該時間步長不滿足顯式精確算法計算得出的穩定性條件，計算結果如圖3所示。可以看出，當材料屈服后，計算得到的等效應力出現了上下抖動現象，此時顯式精確算法的計算不穩定，計算結果錯誤。

2.1.3時間步長dt=1.5×10-7s時

進一步增大了時間步長，其遠不滿足本構計算的穩定性條件。計算結果如圖4所示。從圖4可以看出，當材料屈服后，等效塑性應變歷史曲線呈臺階式上升，四邊形單元在彈性與塑性狀態之間來回跳動，等效應力也變得極不穩定，計算結果與真實值相差巨大。但是當采用傳統的近似算法(半徑回歸法)并仍取時間步長為dt= 1.5×10-7s時，數值計算結果穩定收斂,具體結果如圖5所示。

綜合上述算例可以看出，顯式精確算法的確存在計算穩定性問題，取同樣的時間步長dt=1.5×10-7s，當采用傳統的近似算法(半徑回歸法)得到了正確的結果，而采用顯式精確算法時結果失穩。當時間步長減小至滿足本構計算穩定性條件式(21)時，顯式精確算法給出的計算結果也穩定收斂。

2.2最大時間步長與材料參數和塑性應變率關系

進一步分析滿足本構計算穩定的最大時間步長與材料參數和塑性應變率關系，分別研究各個參數與最大時間步長的關系。分為4組計算，每組只變化1個變量，其余參數的值取表1中的參數值，數值模擬得到滿足本構計算穩定的最大時間步長，其隨各參數的變化如圖6～9所示。

可以看出，本構計算穩定性準則式(21)、(23)與模擬結果符合的較好，最大時間步長與各參量的依賴關系為：與應變率敏感因子β成正比、與靜態條件下屈服強度Y*成正比、與剪切模量G成反比、與塑性應變率成反比。但需要特別指出的是，本構計算穩定性準則式(21)只是顯式精確算法計算穩定的必要性條件。在實際工程計算過程中，為提高其可靠性，可以取一個安全系數。

3 結 論

首先對最常用的Mises類黏塑性材料，重新推導顯式精確算法的計算公式和流程，然后通過理論推導得到顯式精確算法的穩定性條件。通過數值算例，取不同的時間步長來驗證對顯式精確算法的穩定性分析。

數值模擬結果表明，當時間步長過大，不滿足本構計算的穩定性條件時，計算得到的等效屈服應力出現了不穩定現象；而當時間步長滿足穩定性條件時，計算結果準確地描述了材料的復雜變形過程為：彈性加載、塑性加載、彈性卸載、反向彈性加載和反向塑性加載。進一步的數值模擬結果表明：推導得到的穩定性條件可正確預測滿足本構計算穩定的最大時間步長與各參數之間的關系。

[1] Drucker D C. A more fundamental approach to plastic stress-strain relations[M]. Division of Applied Mathematics, Brown University, 1951.

[2] Drucker D C, Prager W, Greenberg H J. Extended limit design theorems for continuous media[J]. Quarterly of Applied Mathematics, 1952,9(4):381-389.

[3] Palmer A C, Maier G, Drucker D C. Convexity of yield surfaces and normality relations for unstable materials or structural elements[J]. Journal of Applied Mechanics, 1967,34(2):464-470.

[4] 李永池,唐之景,胡秀章.關于Drucker公設和塑性本構關系的進一步研究[J].中國科學技術大學學報,1988,18(3):339-345.

Li Yongchi, Tang Zhijing, Hu Xiuzhang. Further study on the drucker postulate and plastic constitutive relations[J]. Journal of China University of Science and Technology, 1988,18(3):339-345.

[5] Hageman L J, Walsh J M. Help, a multi-material Eulerian program for compressible fluid and elastic-plastic flows in two space dimensions and time. Volume 1: AD0726459[R]. Systems Science and Software, La Jolla, California, 1971.

[6] Autodyn theory manual revision 4.3[R]. Century Dynamics Limited, Management Consulting Services, Horsham, United Kingdom, 2000.

[7] Hallquist J O. LS-DYNA theory manual[M]. Livermore: Livermore Software Technology Corporation, 2006.

[8] 李永池,譚福利,姚磊,等.含損傷材料的熱粘塑性本構關系及其應用[J].爆炸與沖擊,2004,24(4):289-298.

Li Yongchi, Tan Fuli, Yao Lei, et al. Thermo-viscoplastic constitutive relation of damaged materials with application[J]. Explosion and Shock Waves, 2004,24(4):289-298.

Abstract: At first, we analyzed the numerical stability of the explicit exact algorithm developed for the viscoplastic material, and then found that the explicit exact algorithm is not absolutely stable, deduced a necessary criterion that the time step should be kept below a certain value to guarantee the constitutive calculation stability. A series of numerical examples were presented to validate the reliability of the present stability analysis on the explicit exact algorithm. The results of the numerical examples show that the effective stress is unstable while the stability criterion for the constitutive calculation is not satisfied, but a complex deformation process including the elastic load, the plastic load, the elastic unload, the reverse elastic load and the reverse plastic load is accurately described while the stability criterion is satisfied. Further numerical results indicate that the stability criterion can accurately predict the relationships between the maximum time step and each parameter.

Keywords: constitutive relation; numerical stability; viscoplastic constitutive; explicit precise algorithm

(責任編輯 王易難)

Thenumericalstabilityoftheconstitutivecalculationonviscoplasticmaterials

Liu Mingtao1,2, Li Yongchi2, Hu Xiuzhang2, Zhang Jie2

(1.InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China; 2.DepartmentofModernMechanics,UniversityofScienceandTechnologyofChina,Hefei230027,Anhui,China)

中國工程物理研究院流體物理研究所發展基金項目(SFZ201401(04)02)

O345國標學科代碼1301520

A

10.11883/1001-1455(2017)05-0969-07

2015-06-29；

2015-10-08

國家自然科學基金項目(11602250)；

劉明濤(1986— )，男，博士，副研究員，liumingtao@caep.cn。