粒子群優化的移動機器人路徑規劃算法

韓 明，劉教民，吳朔媚，王敬濤

(1.石家莊學院 計算機科學與工程學院，石家莊 050035; 2.燕山大學 信息科學與工程學院，河北 秦皇島 066004)

(*通信作者電子郵箱han_ming2008@126.com)

粒子群優化的移動機器人路徑規劃算法

韓 明1,2*，劉教民2，吳朔媚1，王敬濤1

(1.石家莊學院 計算機科學與工程學院，石家莊 050035; 2.燕山大學 信息科學與工程學院，河北 秦皇島 066004)

(*通信作者電子郵箱han_ming2008@126.com)

針對移動機器人在復雜環境下采用傳統方法路徑規劃收斂速度慢和局部最優問題，提出了斥力場下粒子群優化(PSO)的移動機器人路徑規劃算法。首先采用柵格法對機器人的移動路徑進行初步規劃，并將柵格法得到的初步路徑作為粒子的初始種群,根據障礙物的不同形狀和尺寸以及障礙物所占的地圖總面積確定柵格粒度的大小，進而對規劃路徑進行數學建模；然后根據粒子之間的相互協作實現對粒子位置和速度的不斷更新；最后采用障礙物斥力勢場構造高安全性適應度函數，從而得到一條機器人從初始位置到目標的最優路徑。利用Matlab平臺對所提算法進行仿真，結果表明，該算法可以實現復雜環境下路徑尋優和安全避障；同時還通過對比實驗驗證了算法收斂速度快，能解決局部最優問題。

柵格法；粒子群優化；路徑規劃；步進因子；適應度函數

0 引言

智能機器人研究不斷取得新的成果，機器人應用也越來越多地滲透到社會的各個領域。在智能機器人的控制過程中，機器人導航是移動機器人研究的一個重點領域，其中路徑規劃的研究更是機器人導航能力的一個重要體現[1]。

移動機器人的路徑規劃主要目標是使得機器人在從起始點到目標點運動的過程中避免出現碰撞，因此需要尋找一條最優的路徑實現機器人在移動過程中的無碰撞運動[2]。

國內外學者作了大量的研究并提出了很多方法，目前移動機器人的路徑規劃方法主要有全局路徑規劃和局部路徑規劃[3-4],其根據傳感器獲取的信息尋找躲避障礙物的最優路徑，并根據傳感器信息實時調整路徑尋優的策略。可視圖算法[5]根據圖搜索的完備性理論可以實現最優路徑搜索，但是該算法由于計算量大，收斂速度慢，尋優的能力較差，在實時性和可靠性高的要求中無法滿足需求[6]。隨著遺傳算法和神經網絡算法的深入研究，很多學者將這些啟發式的路徑規劃算法引入到了機器人的路徑規劃中實現局部路徑規劃[7]；但這些算法大多存在局部最優的問題，因此為了解決這一問題需要不斷地引入新的算法實現路徑的最優規劃，與此同時增加了算法的復雜度[8]。粒子群優化(Particle Swarm Optimization, PSO)算法[9]具有計算簡單、全局尋優能力強、收斂速度快等優點，在各類多維連續空間優化問題上取得了非常好的效果。許多學者對粒子群優化算法在路徑規劃領域的應用展開了研究。

文獻[10]首次將PSO算法引入移動機器人路徑規劃中，該算法首先采用鏈接圖建立機器人工作空間模型，用Dijkstra 算法求得鏈接圖最短路徑,然后用PSO算法對此路徑進行優化，得到全局最優路徑；但是由于鏈接圖并不能完全體現實際規劃環境中的信息，二次優化后得到的路徑不一定是全局最優路徑, 因此該方法限制了PSO算法的全局尋優能力。文獻[11]利用三次Ferguson樣條算法對移動機器人路徑規劃進行描述，將路徑規劃問題轉化為三次樣條的參數優化問題，為PSO算法在機器人路徑規劃中的應用提供了新的思路；但是，由于PSO算法普遍存在早熟收斂問題使得規劃結果容易陷入局部極值。文獻[12]針對三次樣條早熟收斂問題，提出了具有速度變異的PSO算法，從而改善了早熟收斂問題。針對PSO算法在移動機器人的全局路徑規劃過程中容易出現由于過早收斂導致算法陷入局部最優的問題，文獻[13]提出了一種帶擾動機制的PSO算法。當算法在搜索最優解的過程中陷入局部最優時，采用粒子修正方法產生新的粒子替代原來的粒子，以此來引導算法擺脫局部最優值，搜索可行路徑。為了充分利用PSO算法的全局尋優能力，文獻[14]采用罰函數法表示粒子適應度函數，解決過早收斂的問題；并且為了縮短算法的執行時間，在執行過程中加入碰撞能量測試點，但沒有給出碰撞和距離能量函數的權重比，因此最佳路徑的尋優無法保證。

針對當前移動機器人路徑規劃中的算法收斂速度慢和局部最優的問題，本文將斥力勢場引入PSO算法，首先采用柵格法對機器人的移動路徑進行初步規劃，并將柵格法得到的初步路徑作為粒子的初始種群；然后根據粒子之間的相互協作實現對粒子的位置和速度的不斷更新；最后采用障礙物斥力勢場構造高安全性適應度函數，從而得到一條機器人從開始位置到目標的最優路徑。

1 柵格法實現路徑規劃的數學建模

1.1 柵格法表示機器人工作空間

柵格法將機器人的工作空間表示成一個二維區域，該二維區域進行柵格劃分，分解成一系列的以基本元素為單元的最小柵格，在二維區域的自由區域基本元素取值為0，在圖1中用白色表示；障礙物區域取值為1，在圖中用灰色表示，如圖1所示為機器人工作空間的柵格法表示。

設機器人在平面上運動的二維區域為AS，原點坐標為(0,0)，任意柵格表示為g(x,y)∈AS，其中x表示該柵格所在的行號，y表示該柵格所在的列號；S={1,2,…,n}表示所有柵格的集合。x和y方向的最大值分別為xmax和ymax，機器人行走的步長為δ，則機器人工作空間中的每行和每列的柵格數分別為Nx=xmax/δ和Ny=ymax/δ。對于任意的柵格g(xi,yi)與柵格序號集合互為映射關系，則第i個柵格可表示為：

(1)

其中：mod為模運算，int為向下取整運算。

1.2 確定柵格

由圖1可見，當劃分的柵格粒度越小時，障礙物的表示越精確，但是工作空間劃分得越細所占用的存儲空間會越大，同時會導致算法的復雜度增加；如果選擇的柵格粒度太大又容易造成路徑規劃不準確。因此在柵格法的初步規劃中，粒度大小的選擇是柵格法面臨的主要問題。

在得到機器人工作空間的地圖之后，首先根據障礙物的不同的形狀進行剖分，其中橢圓和不規則圖形按照能覆蓋的最小長方形計算，凸多邊形則進行三角剖分，根據剖分的結果計算地圖中障礙物所占的總面積；然后根據障礙物所占的整個地圖的總面積的比例來決定柵格的粒度大小。柵格粒度大小的計算方法如下：

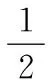
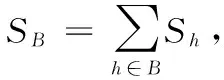
(2)

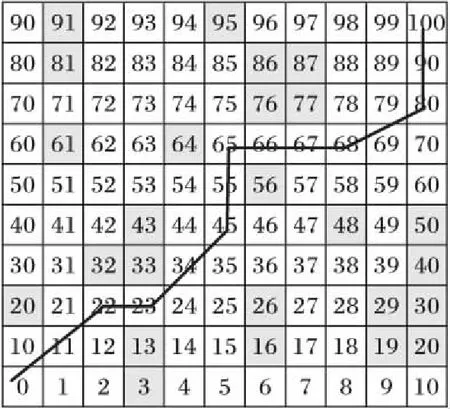
圖1 機器人工作空間柵格法表示Fig. 1 Robot working space represented by grid method

1.3 路徑規劃數學建模

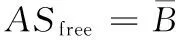
在XOY地圖上建立以為p0為原點，pend為終點的新的X′軸，與之垂直的為Y′軸，則原坐標系中的點在新坐標系中的表示為：

(3)

其中α為X坐標軸與X′的夾角。

將p0pend線段作m+1垂直等分處理，將pend寫為pm+1，其中與X′垂直的平行線簇(l1,l2,…,lm)與X′的交點的序列(p1,p2,…,pm)即為路徑的序列，如圖2所示。

規劃路徑的長度LP為：

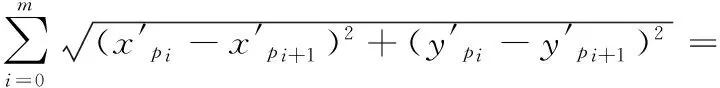
(4)

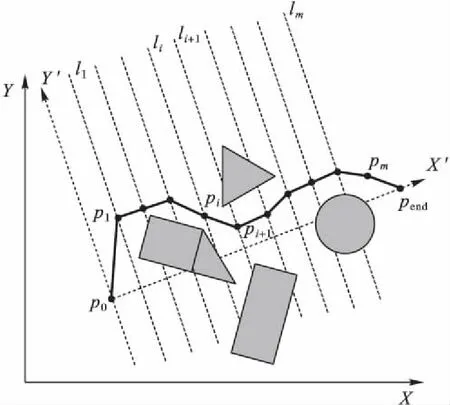
圖2 路徑規劃坐標變換Fig. 2 Path planning coordinate transformation

2 改進的PSO算法實現路徑優化

2.1 粒子速度與位置更新

PSO算法是模擬鳥類覓食行為的速度-位置搜索模型，其粒子的優劣程度由粒子的適應度函數f(x)決定，而且每一個粒子在運行的過程根據自身的個體極值Pbest和整個種群目前最優解的全局極值Gbest來更新位置和速度，以在搜索空間中向更好的位置運動，從而搜索全局最優解[14]。

在1.3節介紹的路徑規劃方法中采用垂直等分的形式按照式(4)進行處理，所以采用PSO算法時的粒子維數為m，而垂線li上點的Y′坐標則構成粒子的位置編碼。

由圖2可見可將粒子定義為由起始點p0經過不同的連接線到達終點pend的距離，即每一個粒子代表一段距離。粒子的適應度函數即為路徑長度表達式(4)，因此當適應度函數的值越小則得到的解即為最優解。

在m維空間中，第i個粒子的位置可表示為向量Xi=(xi1,xi2,…,xim)，通過向量Xi可以確定每個粒子點在鏈接線上的坐標，計算相鄰兩點之間的距離，從而計算適應度值。根據適應度值的大小決定當前的解是否為局部最優，如果是則替換歷史局部最優Pbest。

局部最優Pbest的適應值隨著迭代的進行不斷進行更新;而全局最優Gbest則是與各個Pbest進行比較，如果局部最優Pbest的適應值小于全局最優Gbest則更新全局最優的值為該Pbest的值。

為了得到移動機器人的全局最優路徑，需要在計算過程中不斷更新粒子的速度和位置，其中粒子i表示為向量Xi=(xi1,xi2,…,xim)，粒子的飛行速度為Vi=(νi1,νi2…,νim)。則粒子的速度和位置更新公式如下：

(5)

其中：vi, j(t+1)和xi, j(t)分別表示t時刻第i個粒子在j維的速度和位置；ω為慣性權重因子，ω取值越大則算法具有較高的全局搜索能力，反之則具有較強的局部搜索能力。慣性權重ω隨著迭代次數的增加線性減少，可以使粒子種群在開始時進行大范圍的最優解空間的搜索，然后隨著迭代次數的增加逐漸縮小搜索范圍，從而加強搜索現有解空間的能力。因此本文設計慣性權重ω的取值方法如下：

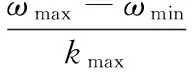
其中：ω的最大值和最小值在本文的實驗中取ωmax=0.9，ωmin=0.4；ki為當前的迭代次數，kmax為最大迭代次數。

c1、c2分別為個體和全局的加速因子，即每個粒子受到個體極值Pbest和全局極值Gbest位置吸引的加速度的權重。加速因子使得每個粒子都具有自我總結并向群體中其他優秀個體學習的能力，從而使粒子在前進的過程中向自己的歷史最優點以及群體內的全局最優點靠近。其中c1調節粒子飛向自身最好位置方向的步長，c2調節粒子飛向全局最好位置方向的步長。r1、r2為隨機數，一般取[0,1]。Pi, j(t)和Gj(t)分別表示到t時刻為止第i個粒子在j維分量搜索到的個體最優位置以及整個種群粒子的第j維分量搜索到的最優位置。

2.2 構造高安全性適應度函數

將人工勢場原理引入到適應度函數的構建中，使移動機器人在人工勢場中移動時，同時受到目標位置的引力場的引力和障礙物的斥力場的斥力兩種力的共同作用。由于斥力場與障礙物有關，因此，機器人在運動的過程中距離障礙物越近則產生的斥力就越大，同時機器人碰觸障礙物的危險系數越高。由于引力場的作用與機器人的運動目標位置有關，因此從算法的復雜度考慮，本文構建高安全性適應度函數時只考慮斥力場的作用。

障礙物附近的斥力場函數表示為：

(6)

其中：η為障礙物的斥力系數；p為機器人在空間中移動時的任意位置，ρ(p)為移動機器人到障礙物的最短距離；ρ0為障礙物的斥力場的作用距離。

為了保證在整個勢力場中只有在目標點位置時全局最小，因此在式(6)的基礎上引入機器人與目標點的相對位置，即在原有的基礎上乘以一個距離因子:

Urep=

(7)

斥力為斥力勢函數的負梯度，則可得斥力為：

Frep=-grad(Urep)=

(8)

機器人在移動過程中由于路徑點的安全性不僅與障礙物的遠近有關，還與空間中障礙物的分布密集程度有關，因此由式(8)可得，移動機器人在空間中的任意位置xi, j處的安全度為：

safei, j=

(9)

其中：s為模板窗口尺寸因子，并且窗口的實際尺寸為(2s+1)2，當s減小時，窗口中會包含較少的障礙物信息，此時安全系數safei, j增大；sign(m,n)為點xi+m, j+n處的障礙物標志，當xi+m, j+n點為障礙物時sign(m,n)=1，否則，sign(m,n)=0。因此可由式(9)計算出機器人在移動的過程中所處位置的安全性系數。

則由式(9)可得路徑Ppath的安全度為：

(10)

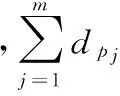
由式(4)和式(10)可得路徑Ppath的優化函數為：

fP=ω1LP+ω2MP

(11)

通過調整加權因子ω1和ω2來調整LP和MP在路徑規劃中所占的比重，從而選擇路徑和安全性均適中的路線。

2.3 路徑優化算法實現

設定義n個m維粒子，采用式(11)作為第i個粒子的適應度函數：

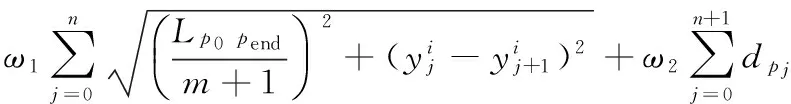
(12)

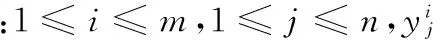
利用適應度函數對所得的路徑集合進行優化, 從而求解全局最優路徑，適應度函數得到的值越小，所得的解越優。

算法實現的具體步驟如下：

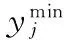
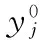
(13)

由式(5)得到粒子的第i個粒子第j維的初始速度和位置為：

(14)

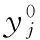
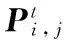
步驟5 對每個粒子按照式(5)中的位置和式(6)的速度進行更新，注意粒子兩端和邊界的約束。

步驟7 如果達到了最大迭代次數或者是最小精度要求，則輸出最優路徑，否則轉到步驟4繼續執行。

算法流程如圖3所示。

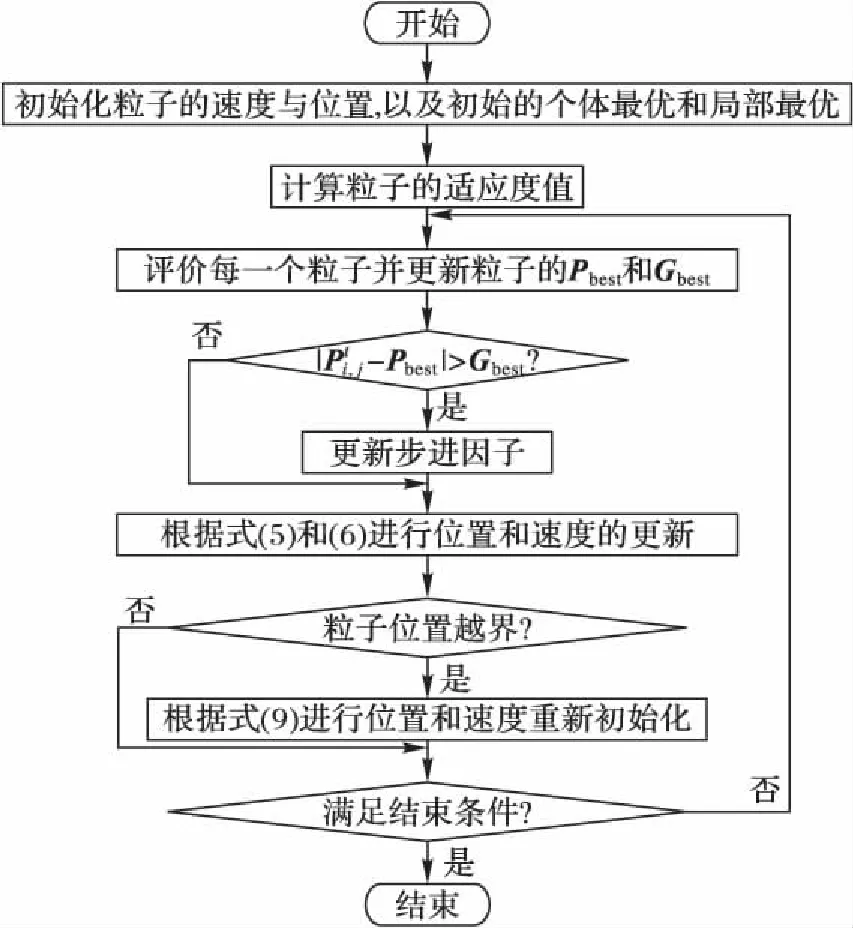
圖3 本文算法流程Fig. 3 Flow chart of the proposed algorithm

3 仿真與分析

為了驗證算法的有效性，以Visual studio 2010為平臺，C# 語言為編程環境進行仿真。實驗的硬件平臺為：Intel Core i5 3.20 GHz CPU；4 GB內存；500 GB硬盤，Windows 10操作系統。

為了驗證本文算法的有效性，在相同的環境模型下將本文方法與線性遞減慣性權重粒子群優化算法(Linearly Decreasing Weight Particle Swarm Optimization, LDWPSO)[13]進行對比實驗。

3.1 最優路徑與收斂性比較

采用1.2節的方法確定柵格，經過多次對不同實驗環境(包括本文的實驗環境1、2以及圖8所示環境)的測試，取lmax=20，lmin=3時柵格粒度較適合實驗目的。實驗環境1和2相對障礙物較少，因此柵格粒度較大；而圖8中的實驗環境下障礙物較密，因此柵格粒度較小。

實驗環境1參數描述：實驗環境采用15×15方格的環境，環境中障礙物數目為42，每一個方格表示一個障礙物。移動機器人運動起點為(0,0)，終點位置為(14,14)。

如圖4所示為本文算法與LDWPSO的最優解對比結果。LDWPSO算法在第32次迭代時找到了最優解，本文算法則是在第25次迭代時已經找到了符合終止條件的最優解。因此從算法的收斂性上來看本文算法優于LDWPSO算法，并且尋找的最優路徑的柵格長度本文算法為17，LDWPSO算法為19。

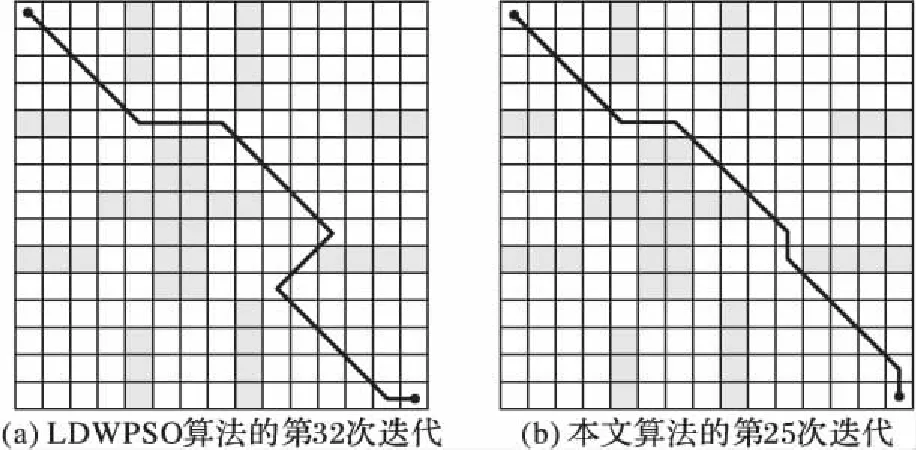
圖4 環境1最優路徑對比Fig. 4 Comparison of optimal path in environment 1

圖5給出了本文算法的避障過程，在由第17次向第18次迭代的過程中，能夠明顯地躲避障礙，并且在搜索的過程中搜索范圍較大，能夠跳出局部最優。

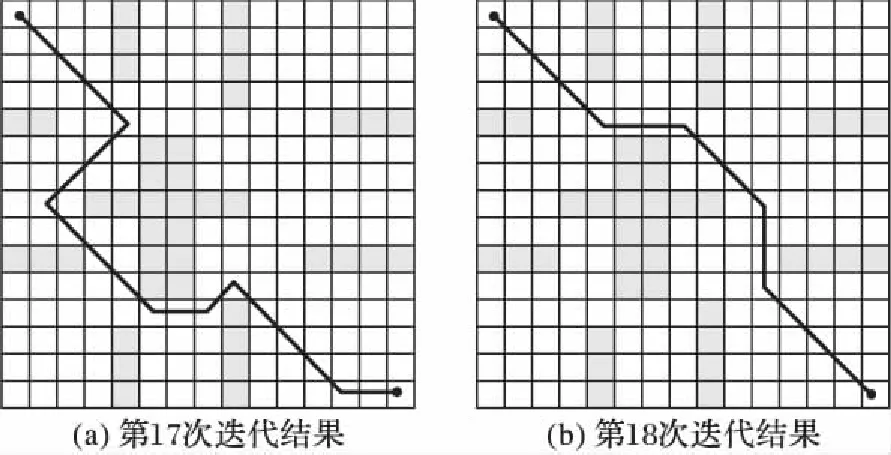
圖5 本文算法的第17次迭代和第18次迭代的避障情況Fig. 5 Obstacle avoidance of 17th and 18th iterations by the proposed algorithm

實驗環境2參數描述：實驗環境采用10×10方格的環境，環境中障礙物數目為31，每一個方格表示一個障礙物，并且分布無序；移動機器人的起始位置為(0,0)，終點位置為(9,9)。

由圖6可以看出本文算法克服了局部最優的缺陷并成功搜索到了最優路徑，本文算法搜索路徑的柵格長度為12，而LDWPSO算法則為14。

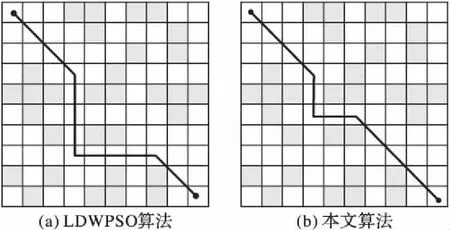
圖6 環境2最優路徑對比Fig. 6 Comparison of optimal path in environment 2

圖7給出了兩種算法的收斂性比較，可以看出：本文算法在50次的迭代過程中都在第6次找到了局部最優解，第12次迭代之后找到了最優解，并穩定在最優解；而LDWPSO算法則在第17次達到了局部最優并且沒有跳出局部最優解。因此從算法的收斂性和克服局部最優解方面本文算法優于LDWPSO算法。

3.2 本文算法不同實驗環境最優路徑對比

在本實驗中采用相同的實驗地圖，但是實驗環境中的障礙物數目、位置以及狀態不同。實驗結果如圖8所示，由圖可以看出對于不同的實驗環境，本文算法都能得到最優的路徑規劃，說明本文算法對于復雜環境具有較高的適應性。

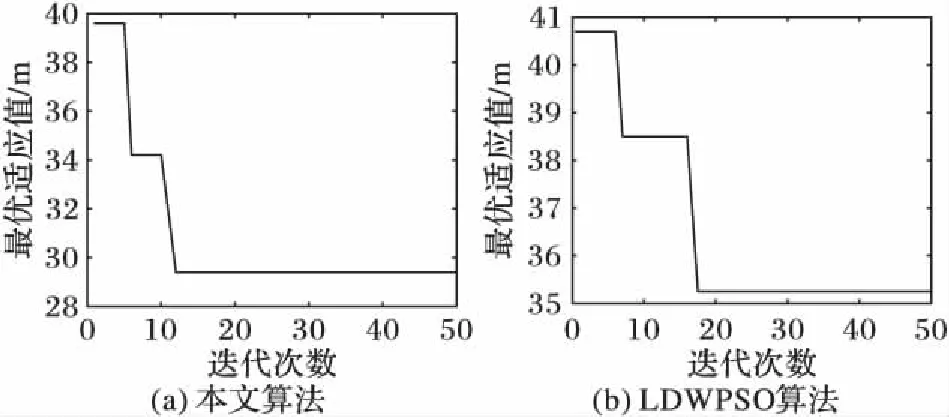
圖7 兩種算法收斂性比較Fig. 7 Convergence comparison of two algorithms

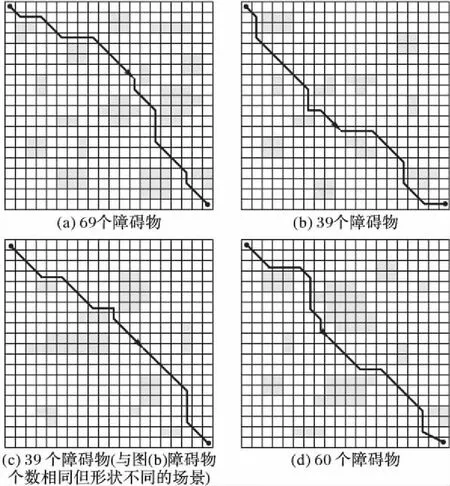
圖8 不同環境的最優路徑規劃Fig. 8 Optimal path planning in different environments

4 結語

本文針對傳統的粒子群優化(PSO)算法實現移動機器人路徑規劃中的局部極值問題以及適應度函數在計算過程中的粒子安全性問題，提出了斥力勢場下粒子群優化的移動機器人路徑規劃算法，該算法為移動機器人在復雜環境下的路徑規劃提供了一種有效的選擇。該算法主要有以下特點：1)該算法利用柵格法實現機器人路徑的初步規劃，并將初始規劃的路徑作為粒子的初始種群；2)根據粒子之間的相互協作實現對粒子的位置和速度的不斷更新，解決路徑規劃中的局部極值問題；3)采用障礙物斥力勢場構造高安全性適應度函數。通過實驗仿真驗證本文算法能獲得路徑尋優的最優解，并且算法的收斂速度快。

References)

[1] 朱大奇,顏明重.移動機器人路徑規劃技術綜述 [J].控制與決策,2010,25(7):961-967. (ZHU D Q, YAN M Z. Survey on technology of mobile robot path planning [J]. Control and Decision, 2010, 25(7): 961-967.)

[2] 蔡自興,賀漢根,陳虹.未知環境中移動機器人導航控制理論與方法[M]. 北京：科學出版社,2009:8-12. (CAI Z X, HE H G, CHEN H, Mobile robot navigation in unknown environment control theory and method [M]. Beijing: Science Press,2009:8-12.)

[3] CLERC M, KENNEDY J. The particle swarm-explosion, stability and convergence in a multidimensional complex space [J]. IEEE Transactions on Evolutionary Computer, 2002, 6(1): 58-73.

[4] SHI P, HUA J N. Mobile Robot dynamic path planning based on artificial potential field approach [J]. Advanced Materials Research, 2012, 490-495: 994-998．

[5] SUD A, ANDERSEN E, CURTIS S, et al. Real-time path planning in dynamic virtual environments using multiagent navigation graphs [J]. IEEE Transactions on Visualization and Computer Graphics, 2008, 4(3): 526-538.

[6] TAVARES R S, MARTINS T C, TSUZUKI M S G. Simulated annealing with adaptive neighborhood: a case study in off-line robot path planning [J]. Expert Systems with Applications, 2011, 38(4): 2951-2965.

[7] GHATEE M, MOHADES A. Motion planning in order to optimize the length and clearance applying a Hopfield neural network [J]. Expert Systems with Applications, 2009, 36(3): 4688-4695.

[8] 杜宗宗,劉國棟.基于遺傳模擬退火算法的移動機器人路徑規劃[J].計算機仿真,2009,26(12):118-121. (DU Z Z, LIU G D. Path planning of mobile robot based on genetically simulated annealing algorithm[J]. Computer Simulation, 2009, 26(12): 118-121.)

[9] ZENG N, ZHANG H, CHEN Y, et al. Path planning for intelligent robot based on switching local evolutionary PSO algorithm [J]. Assembly Automation, 2016, 36(2): 120-126.

[10] 秦元慶,孫德寶,李寧，等.基于粒子群算法的移動機器人路徑規劃[J].機器人,2014,26(3):222-225. (QIN Y Q, SUN D B, LI N, et al. Path planning for mobile robot based on particle swarm optimization [J]. Robot, 2014, 26(3): 222-225.)

[11] SHENG J W, HE G H, GUO W B et al. An improved artificial potential field algorithm for virtual human path planning [C]// Proceedings of the 2010 International Conference on Entertainment for Education Digital Techniques & Systems, LNCS 6249. Berlin: Springer-Verlag, 2010: 592-601

[12] SETHANAN K, NEUNGMATCHA W. Multi-objective particle swarm optimization for mechanical harvester route planning of sugarcane field operations [J]. European Journal of Operational Research, 2016, 252(3): 969-984.

[13] TANG Z, ZHOU Y. A glowworm swarm optimization algorithm for uninhabited combat air vehicle path planning [J]. Journal of Intelligent Systems, 2014, 24(1): 69-83.

[14] TANG B, ZHU Z, LUO J. A convergence-guaranteed particle swarm optimization method for mobile robot global path planning [J]. Assembly Automation, 2017, 37(1): 114-129.

This work is partially supported by the Science and Technology Plan Projects of Hebei Province (15220327, 16222101D- 2), the Youth Topnotch Talent Program of Hebei Universities and Colleges (BJ2017105).

HANMing, born in 1984, Ph. D., lecturer. His research interests include intelligence robot, pattern recognition and control.

LIUJiaomin, born in 1958, Ph. D., professor. His research interests include intelligence control, pattern recognition.

WUShuomei, born in 1977, M. S., lecturer. Her research interests include pattern recognition, machine vision.

WANGJingtao, born in 1984, M. S., assistant. Her research interests include intelligence computing, pattern recognition.

Pathplanningalgorithmofmobilerobotbasedonparticleswarmoptimization

HAN Ming1,2*, LIU Jiaomin2, WU Shuomei1, WANG Jingtao1

(1.CollegeofComputerScienceandEngineering,ShijiazhuangUniversity,ShijiazhuangHebei050035,China；2.SchoolofInformationScienceandEngineering,YanshanUniversity,QinhuangdaoHebei066004,China)

Concerning the slow convergence and local optimum of the traditional robot path planning algorithms in complicated enviroment, a new path planning algorithm for mobile robots based on Particle Swarm Optimization (PSO)algorithm in repulsion potential field was proposed. Firstly, the grid method was used to give a preliminary path planning of robot, which was regarded as the initial particle population. The size of grids was determined by the obstacles of different shapes and sizes and the total area of obstacles in the map, then mathematical modeling of the planning path was completed. Secondly, the particle position and speed were constantly updated through the cooperation between particles. Finally, the high-security fitness function was constructed using the repulsion potential field of obstacles to obtain an optimal path from starting point to target of robot. Simulation experiment was carried out with Matlab. The experimental results show that the proposed algorithm can implement path optimization and safely avoid obstacles in a complex environment; the contrast experimental results indicat that the proposed algorithm converges fast and can solve the local optimum problem.

grid method; Particle Swarm Optimization (PSO); path planning; progress factor; fitness function

TP391; TP18

A

2017- 01- 17;

2017- 03- 05。

河北省科技計劃項目(15220327, 16222101D- 2)；河北省高等學校青年拔尖人才計劃項目(BJ2017105)。

韓明(1984—)，男，河北行唐人，講師，博士，CCF會員，主要研究方向：智能機器人、模式識別與控制； 劉教民(1958—)，男，河南西峽人，教授，博士生導師，博士，CCF會員，主要研究方向：智能控制、模式識別； 吳朔媚(1977—)，女，河北邢臺人，講師，碩士，主要研究方向：模式識別、機器視覺； 王敬濤(1984—)，女，河北邯鄲人，助教，碩士，主要研究方向：智能計算、模式識別。

1001- 9081(2017)08- 2258- 06

10.11772/j.issn.1001- 9081.2017.08.2258