加權稀疏信號重構的近場源定位方法

李雙，劉驍，胡順仁，何為

?

加權稀疏信號重構的近場源定位方法

李雙1，劉驍1，胡順仁1，何為2

(1. 重慶理工大學電氣與電子工程學院，重慶400050； 2.中國科學院上海微系統與信息技術研究所無線傳感網與通信重點實驗室，上海201800)

針對近場源定位問題，提出了一種使用加權L1范數優化進行稀疏信號重構的近場源定位方法。該定位方法分步完成目標的方位和距離估計。為了避免二維優化問題出現，首先利用均勻線陣的對稱特性，通過菲涅爾近似，將二維參數估計的近場定位問題轉換為類遠場陣列的一維參數估計問題，接著將該一維參數估計問題轉換為稀疏信號重構問題，通過類MUSIC權向量的構造，使用加權L1范數優化方法重構稀疏空間譜得到目標波達方向；在得到信號波達方向之后，再利用稀疏信號重構的思想求解信號源到陣列的距離。最后，通過數字仿真驗證了算法在估計精度和分辨率等方面的優良性能。

波達方向估計；距離估計；近場源定位；加權稀疏信號重構

0 引言

近年來，近場源的定位逐漸成為陣列信號處理領域中一個重要的發展方向，廣泛用于聲源定位[1]和水下無線傳感器網絡[2]等。當聲源目標距離陣列中心距離很近，遠場條件不再滿足的時候，都必須以近場模型進行目標定位。立足于近場源定位，國內外學者提出了許多方法，主要有基于高階累積量的算法[3-5]，但該類算法不能用于高斯信號，并且需要計算累積量，導致需要較大的快拍數；還有基于對稱陣列的算法等[6-8]，該類算法的陣列孔徑損失較嚴重。

隨著稀疏信號重構在遠場DOA估計中的成功運用[9]，以及該類算法在抗噪聲能力、快拍數、分辨率等方面展現出的優異性能，使得越來越多的學者在近場定位方面也展開了基于稀疏信號重構的研究。Wang等人[10]提出了基于累積量稀疏表示的混合源定位算法。Tian等人[11]基于近場與遠場的混合源，提出MUSIC與稀疏表示的聯合算法，具有更好的估計性能。梁國龍等人[12]構造虛擬遠場陣列接收信號的協方差矩陣，將近場條件波達方向和距離的二維參數估計問題轉換成兩個一維稀疏信號的恢復問題。Hu等人[13]通過接收信號協方差矩陣的反對角元素稀疏表示分步實現了DOA和距離的稀疏估計，該方法與文獻[12]的方法類似，但具有更低的計算復雜度，同時，同樣陣元數條件下可以檢測的信號源數更多。

本文基于文獻[13]中距離和DOA參數的分離方法的思想，采用加權L1范數進行信號復原，提出了一種基于加權稀疏信號重構的近場源定位算法。首先利用陣列的對稱特性，分離傳播時延中距離和DOA兩個參數，將距離和DOA聯合二維估計的近場源定位問題轉換為虛擬的遠場DOA估計問題，利用加權L1范數進行稀疏信號重構，得到目標的DOA估計；在得到目標DOA估計后，再利用基于L1范數的奇異值分解(L1-SVD)方法[14]得到距離估計，從而分步完成近場目標的距離和DOA的聯合估計。

1 信號模型

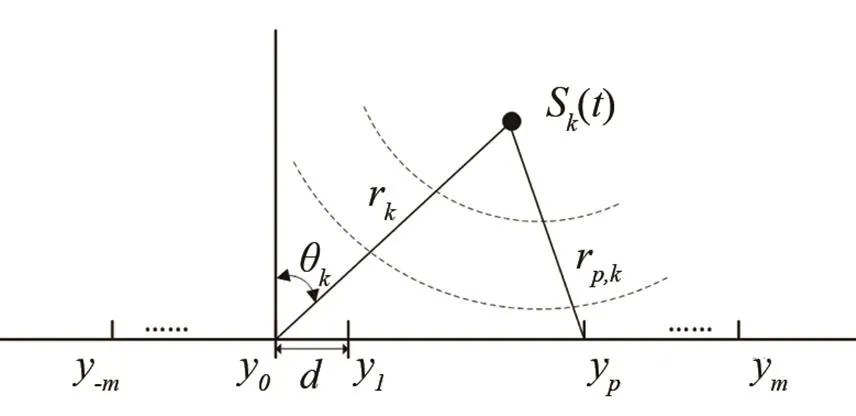
圖1 陣列幾何結構

把式(2)用二階泰勒級數展開，即得到所謂的菲涅爾近似[4]：

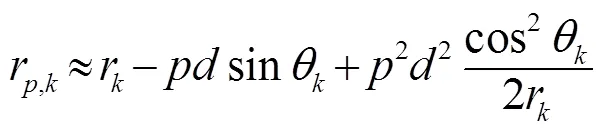
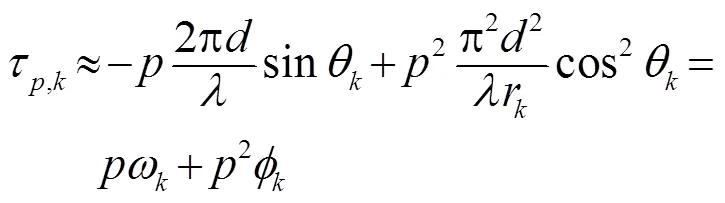
為使得推導方便，作如下假設：

(1) 陣列接收信號之間相互獨立，并且每個信號的方位角都不一致；

(2) 信號與噪聲之間相互獨立；

(3) 噪聲之間相互獨立，并且為高斯白噪聲。

2 DOA和距離參數分離

根據假設條件，第與第個陣元間的協方差可以表示為[13]：

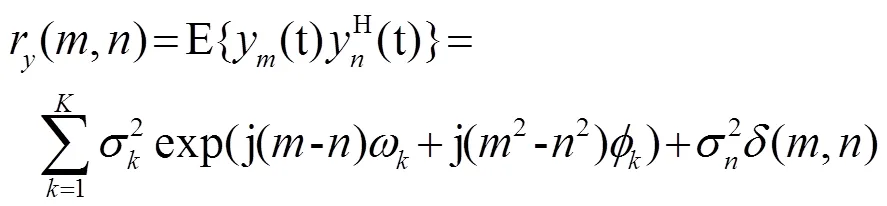
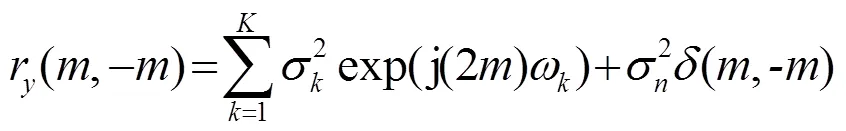
由此，可以利用對稱陣列的互相關性，把最初的DOA和距離的二維估計轉化為一維的DOA估計，建立起一個虛擬遠場源的場景：

3 DOA估計

3.1 類MUSIC方法[15]

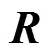
對矩陣進行特征值分解，有

對式(12)的類MUSIC空間譜進行譜峰搜索，可以得到信號源的DOA估計。本文以式(12)的空間譜的倒數作為權向量進行加權范數的稀疏信號重構，完成DOA估計，以提高DOA估計算法的性能。

3.2 加權范數恢復方法

定義權向量：

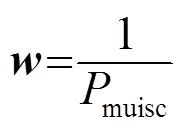
以類MUSIC空間譜函數作為權向量對式(13)進行加權L1范數的稀疏信號重構，即：

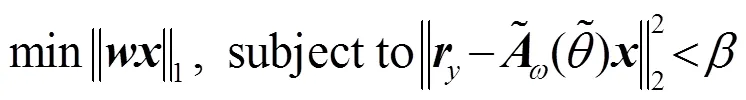
4 近場源距離估計

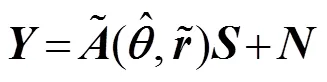
寫成單列的形式為

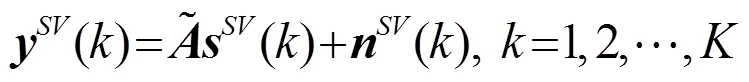
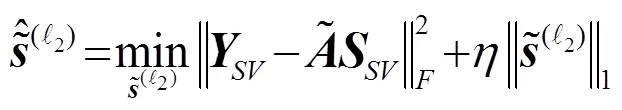
綜上，本文定位算法分為如下步驟：

5 仿真與對比

5.1 空間譜和距離譜比較

5.2 估計誤差

下面對上述兩種方法的DOA估計誤差進行比較。DOA估計的均方誤差定義如下：

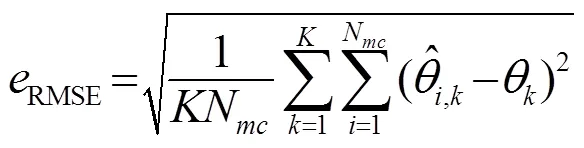
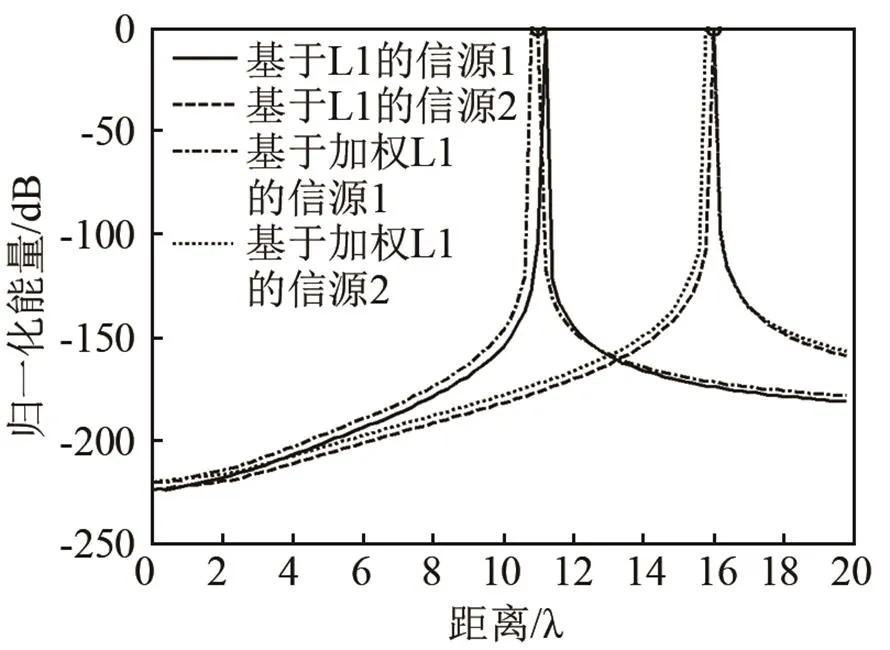
圖3 不同信號源的距離譜圖比較

5.3 分辨率

分辨率反映了算法對空間兩個相隔較近的信號的分辨能力，其定義如下：如果第次試驗估計結果滿足如下條件：

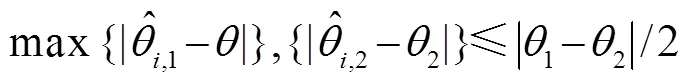
其中，和分別為第i次試驗中第一個和第二個信號源的估計值，則認為第i次試驗中兩個信源成功分辨。

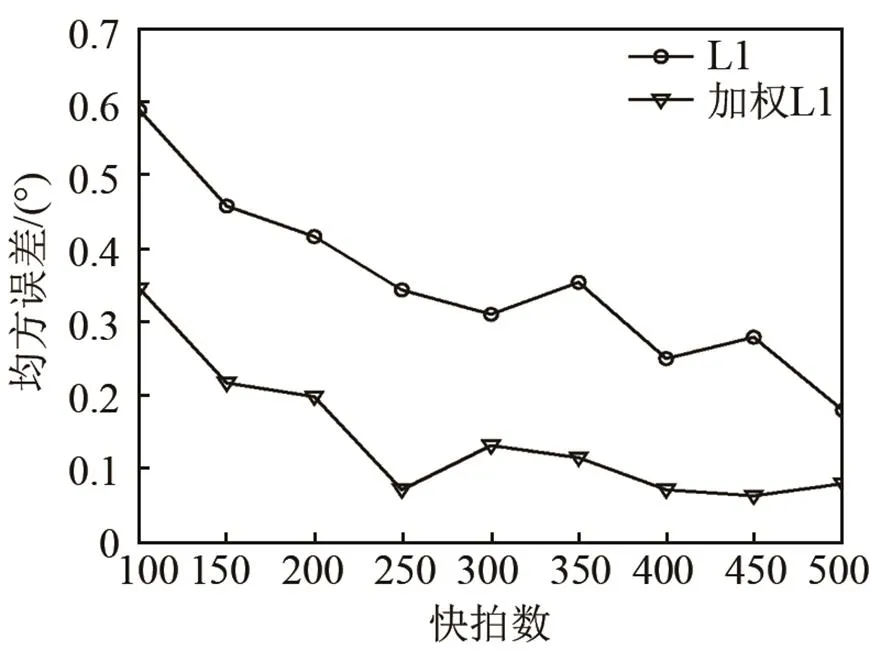
圖5 均方誤差隨快拍數變化的關系圖

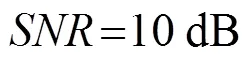
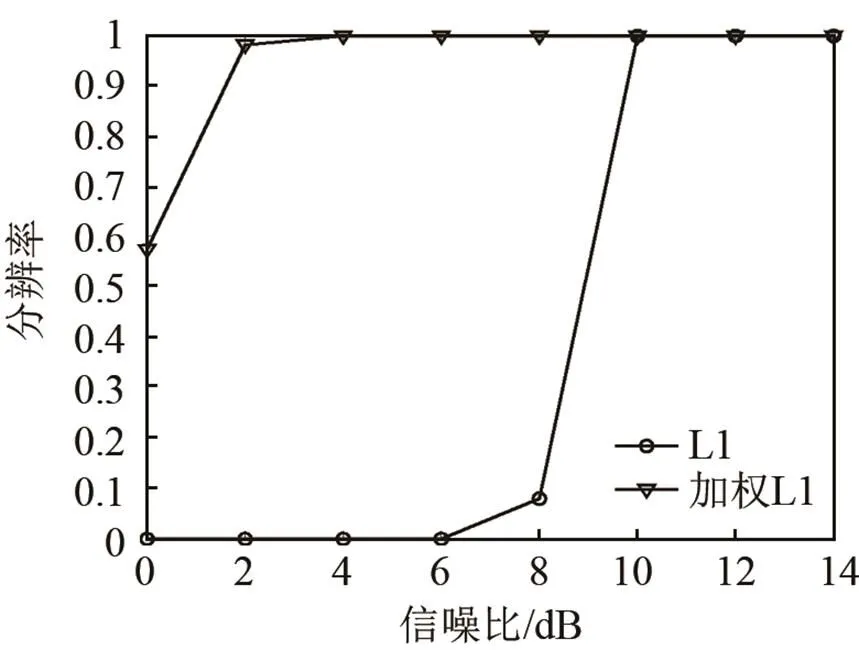
圖6 分辨率與信噪比關系圖

圖7 分辨率與快拍數關系圖

6 結論

本文提出了基于加權稀疏信號重構的近場源定位算法。通過構造類遠場的協方差矩陣，運用類MUSIC算法估計出的角度譜作為權向量，基于加權范數進行稀疏信號恢復實現DOA估計；再利用所得角度，運用L1-SVD算法估計近場源距離。本文提出的方法只需要計算二階統計量，不需要額外的參數配對，和同類算法相比，本文所提出的方法具有更低的估計誤差和更高的分辨概率。由于正則化參數的選取對算法結果影響較大，今后擬對正則化參數如何選擇進行研究和探討。

[1] 王偉, 倪明, 許將明, 等. 室內五元十字陣被動聲定位[J]. 聲學技術, 2011, 30(1): 102-106.WANG Wei, NI Ming, XU Jiangming, et al. Passive localization of indoor acoustic target by five-element cross array[J]. Technical Acoustics, 2011, 30(1): 102-106.

[2] 王靜, 陳建峰, 張立杰, 等. 水下無線傳感器網絡[J]. 聲學技術, 2009, 28(1), 89-95. WANG Jing, CHEN Janfeng, ZHANG Lijie, et al. Underwater sensor networks[J]. Technical Acoustics, 2009, 28(1): 89-95.

[3] LIANG Junli, LIU Ding. Passive localization of near-field sources using cumulant[J]. IEEE Sensors Journal, 2009, 9(8): 953-960.

[4] LIANG Junli, LIU Ding. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108-120.

[5] WU Yuntao, MA Lin, HOU Chaohuan, et al., Subspace-based method for joint range and DOA estimation of multiple near-field sources[J]. Signal Processing, 2006, 86(8): 2129-2133.

[6] 劉亮, 陶建武, 黃家才. 基于稀疏對稱陣列的近場源定位[J]. 電子學報, 2009, 37(6): 1307-1312.LIU Liang, TAO Jianwu, HUANG Jiacai. Near-Field source localization based on sparse symmetric array[J]. Chinese Journal of Electronics, 2009, 37(6): 1307-1312.

[7] ZHAO Yinghui. Dinstel Amanda, Azimi-Sadjadi Mahmood R, et al. Localization of near-field sources in sonar data using the sparse representation framework[C]//Waikoloa, HI: IEEE OCEANS 2011 MTS, 2011, 1-6.

[8] XIE Jian, TAO Haihong, RAO Xuan, et al. Comments on “Near-Field Source Localization via Symmetric Subarrays”[J]. IEEE Signal Processing Letters, 2015, 5(22): 643-644.

[9] HU Nan, YE Zhongfu, XU Xu, et al. DOA estimation for sparse array via sparse signal reconstruction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 760-773.

[10] WANG Bo, LIU Juanjuan, SUN Xiaoying. Mixed sources localization based on sparse signal reconstruction[J]. IEEE Signal Processing Letters, 2012, 19(8): 487-490.

[11] TIAN Ye, SUN Xiaoying. Passive localization of mixed sources jointly using music and sparse signal reconstruction[J]. AEU - International Journal of Electronics and Communications, 2014, 68(6): 534–539.

[12] 梁國龍, 韓博, 林旺生, 等. 基于稀疏信號重構的近場源定位[J]. 電子學報, 2014, 42(6): 1041-1046.LIANG Guolong, HAN Bo, LIN Wangsheng, et al. Near-field sources localization based on sparse signal reconstruction[J]. Chinese Journal of Electronics, 2014, 42(6): 1041-1046.

[13] Hu Keke, Chepuri Sundeep Prabhakar, Leus Geert. Near-field source localization using sparse recovery techniques[C]// Bangalore: IEEE 2014 International Conference on Signal Processing and Communications (SPCOM), IEEE, 2014, 1-5.

[14] Malioutov D, ?etin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022.

[15] 劉鴻博, 陳福深. 一種近場無源定位方法[C]//長沙: 2007年光電探測與制導技術的發展與應用研討會, 2007: 610-613. LIU Hongbo, CHEN Fushen. A source localization method in the near-field[C]//Changsha: Symposium on the Development and Application of the Technology of Photoelectric Detection and Guidance, 2007: 610-613.

[16] Grant Michael, Boyd Stephen, YE Yinyu. CVX: Matlab software for disciplined convex programming[EB/OL]. 2008 [2016-06-23] http://cvxr.com/cvx/.

Near-field source localization based on weighted sparse signal recovery

LI Shuang1, LIU Xiao1, HU Shun-ren1, HE Wei2

(1.School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400050, China; 2. Key Laboratory of Wireless Sensor Networks and Communication, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 201800, China)

In this paper, a source localization method is proposed based on sparse signal recovery by utilizing a weighted L1-norm penalty. The direction-of-arrival and range are estimated by two steps. First, the source localization problem, which needs two-dimensional parameter estimation, is transformed into a one-dimensional parameter estimation problem in far-field by use of the symmetry of uniform linear array and Fresnel approximation. After that, the problem is solved by finding the sparse spatial spectrum using weighted L1-norm penalty. Then the idea of sparse signal recovery is employed again to estimate the range between the source and the array. Finally, the superior performance of the method is demonstrated by numerical simulation in terms of accuracy and resolution ability.

DOA (direction-of-arrival) estimation; range estimation; near-field source localization; sparse signal recovery using a weighted penalty

TN911.72

A

1000-3630(2017)-01-0075-06

10.16300/j.cnki.1000-3630.2017.01.014

2016-04-06;

2016-06-15

重慶市基礎與前沿研究計劃項目(cstc2015jcyjA040055); 重慶市教委科學技術研究項目(KJ1500917，KJ1500934)

李雙(1986－), 男, 四川南充人, 博士, 講師, 研究方向為陣列信號處理及應用。

李雙, E-mail: lis@cqut.edu.cn。