數學解題反思：層次性及其案例（上）

潘小明

早在上世紀80年代，Zeichner & Liston就曾根據Van Manen的研究提出了關于學習者反思具有低、中、高等不同層次的觀點[1][2]。國內也有學者把反思劃分為“前反思”“準反思”和“反思”三種不同水平的反思層次[3]。那么，就中學生數學解題這一特定的實踐而言，實踐者的實踐反思在層次上有怎樣的特點？針對這一現實而基本的問題，研究者于2015年3月開始對江蘇省中部地區某農村初中學生數學解題反思的行為進行了跟蹤研究，初步概括了初中生數學解題反思的常識性、知識性、技術性和思想性特點，本文擬結合具體案例對這4種不同層次的反思進行簡要的描述與分析。

1.解題反思的常識性層次

這種層面的反思表現對當下數學解題活動瞬間的常識化思維，本質上是一種對數學解題活動沒有深層思考的準反思。研究者在調研時發現，成績較差的學生在數學解題過程中如果遇到了自己熟悉的數學刺激或問題情境，就容易表現出常規式、習慣性“想一想”“推一推”的數學活動方式。他們的數學解題行為更多地表現出一種自動化、半自動化的特性。個別訪談時發現，一些學生在數學解題中之所以出現數學錯誤，是因為他們的反思始終處于一種即時化、意識流式的常識狀態，在數學思維上沒有或很少涉及下一步該如何行動以及為什么這樣行動。從本質上看，與其說這些學生處于數學解題反思狀態中，還不如說他們僅僅是處于數學解題活動的準反思狀態中。

案例1求4m的倒數。

由于學生的解題反思水平僅僅處于常識性的層次，他們在解題過程中就容易被一些看起來合情合理的常識所迷惑。比如，正數是表示大于0的數，對應的符號用+表示，負數是表示小于0的數，對應的符號用-表示，這是一種常識。在特定的數學情境下，這種所謂的常識會掩蓋數學整體的意義，稍有不慎，就有可能犯實質性的數學錯誤。一個典型的例子是，在對學生進行“比較4m與-4m大小”這一類題的測試中，有學生就因為所謂的常識而不加分析地斷定4m是正數、-4m是負數，并由此得到4m>-4m的唯一答案，而沒有認識到字母m除了可取正值，還可取負值或0，4m與-4m的大小比較要根據m的取值進行討論。總的來說，僅僅處于常識性反思層面的學生在數學解題過程中并非沒有“想一想”“推一推”，只是他們的“想一想”“推一推”更多地停留于非常淺顯的數學思維層次。

2.解題反思的知識性層次

解題的第一要務是把題目解出來，基于這種基本使命，學生對題目“究竟怎么解決”“究竟怎么做”往往有較高的關注度，由此也使他們的解題反思表現出知識性層次的特點。這種特點表現為學生對相關數學題目中相關概念、命題、法則“所知”的反思，并因此產生對問題中相關要素界定的思維。比如，有學生在討論中會問：“這句話是什么意思？”“這個式子是什么含義？”“條件或結論在說什么？”知識性層次解題反思也會表現為學生對相關數學題目中相關概念、命題、法則“所識”的反思。這是學生基于個人經驗、見識對當下數學問題及其解答過程中相關刺激、相關要素進行必要的辨認、識別、判斷，并據此產生進一步問題表征、方法匹配、解題決策的解題行為。可見，在知識性層次的解題反思中，學生不僅結合個人的數學活動經驗對當下的事實性、命題性和程序性三類數學知識進行必要的提取，而且據此進一步揭示待解數學題目的一些特征，初步分析問題所屬的類型，基于“所知”“所識”進行解題思路、模式和經驗的匹配與對接。

案例2在一節習題課上，數學教師要求學生解答如下的一道選擇題：

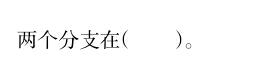
A.第一、二象限B.第一、三象限

C.第二、四象限D.第三、四象限

案例3下午4點到5點，電視里播出一部動畫片，開始時分針與時針正好成一條直線，結束時兩針正好重合，試求解這部動畫片播了多少時間？

案例描述與分析在這一測試中，研究者要求3名學生就本題的解答進行出聲思維。為了說明出聲思維的含義，研究者本人結合其他數學題目的思考過程進行了必要的示范。

研究者發現，被試學生拿到題目后，先是讀了兩遍題目，然后準備在作業紙上書寫。不過，他們很快放下了筆，因為他們不知道寫什么。研究者啟發他們：“動筆之前，好好想一想喲！”但后來發現有2位學生開始自言自語：“這好像是小學里的算術問題！”“什么類型的呢？”“我想想！”“行程問題？噢，不，不是的。”“有點像追及問題。”“我如果把分針和時針分別看成2個人，不就是分針這個人追趕時針這個人，追趕的時間不就是動畫片播放的時間嗎？”“嗯，解答有了。只要假設時針行走的速度為每小時1格，則分針行走的速度就是每小時12格，如果這部動畫片播了x小時，那么分針行走到與時針重合時也需要x小時，根據題目的信息，因為分針比時針多走6格，所以可以列出方程：12x=1·x+6，嗯，搞定！”在該案例中，類似的問題通常被稱為鐘面問題。開始時，分針與時針成一條直線，所以相差180毅；結束時兩針重合，所以相差0毅。有學生在表征問題階段，聯想到小學階段應用題中的追及問題，本身體現了對數學模式的識別。據此，這些學生不僅重新理解了待求解的數學題目，而且解題時的思路顯得十分清晰。

中學生在數學解題反思中的“所識”直接影響著其“所知”的狀態。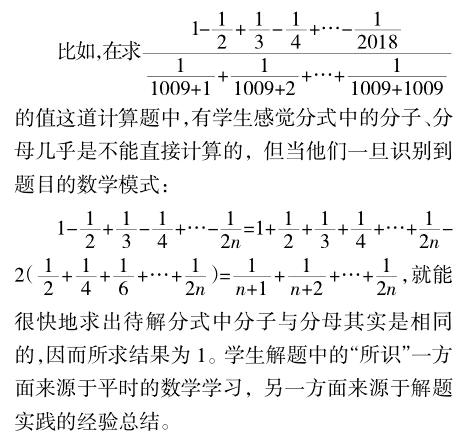

（待續）endprint