一種改進的FLS-SVM分類辨識模型及其應用

左紅艷，王濤生

?

一種改進的FLS-SVM分類辨識模型及其應用

左紅艷1, 2，王濤生2

(1. 中南大學資源與安全工程學院，湖南長沙，410083；2．湖南涉外經濟學院商學院，湖南長沙，410205)

采用三角形函數隸屬度法確定模糊最小二乘支持向量機(fuzzy least squares support vector machine, FLS-SVM)輸入參數隸屬度，采用自適應變尺度混沌免疫算法優化FLS-SVM的參數，從而構建改進模糊最小二乘支持向量機(improved fuzzy least squares support vector machines, IFLS-SVM)分類辨識模型，用Ripley數據集、MONK數據集和PIMA數據集進行仿真實驗，并用于地下金屬礦山采場信號分類辨識與中國國際貿易安全分類辨識。研究結果表明：與LS-SVM分類辨識模型和FLS-SVM分類辨識模型相比，IFLS-SVM分類辨識模型能有效提高帶噪聲點和異常點數據集的分類精度，且分類辨識精度相對誤差較小。

混沌免疫算法；模糊最小二乘支持向量機；分類辨識

對于小樣本條件下的高維模式分類辨識和非線性回歸問題，建立在統計學習理論的VC維理論和結構風險最小原理基礎上的支持向量機(support vector machine，SVM)[1?3]比神經網絡分類、決策樹分類和模糊分類具有更多的優勢，它可以根據有限的樣本信息在模型的復雜性和學習能力之間尋求最佳折中，以求獲得最強的推廣能力，但其抗噪聲能力弱，過擬合和多類分類精度低等，這成為制約其廣泛應用于模式識別、信號分類處理和時間序列預測等領域[4?7]的瓶頸。考慮到模糊理論具有非線性映射能力強、可有效表示模糊信息以及不確定性等特點，人們提出模糊支持向量機(fuzzy support vector machines, FSVM)[8?9]和模糊最小二乘支持向量機(fuzzy least squares support vector machine, FLS-SVM)[10?11]等改進型支持向量機，以消除樣本中噪聲的影響，使改進型支持向量機結構更透明和具有更強的推理能力。由于模糊支持向量機和模糊最小二乘支持向量機[12?13]等改進型支持向量機要求隸屬度函數必須能客觀、準確地反映系統中樣本存在的不確定性，且其正則化參數和核參數優化對其分類精度有很大影響[14?15]，因此，如何有效構造隸屬度函數來區分樣本集中噪聲或野值點和采用有效的優化算法對正則化參數和核參數進行優化十分重要[16?17]。考慮到三角形隸屬度函數法能客觀、準確地反映系統中樣本存在的不確定性[18]，本文作者采用三角形隸屬度函數法確定FLS-SVM(fuzzy least squares support vector machine)的隸屬度，同時采用自適應變尺度混沌免疫算法優化FLS-SVM的參數，建立改進模糊最小二乘支持向量機(improved fuzzy least squares support vector machines, IFLS-SVM)分類辨識模型，進行數據集分類仿真實驗及實例應用。

1 改進FLS-SVM分類辨識模型構建

由于影響FLS-SVM分類精度的因素主要包括正則化參數和核參數是否優化、隸屬度函數是否客觀和準確地反映樣本存在的不確定性，為此，采用三角形隸屬度函數法確定FLS-SVM的隸屬度，采用自適應變尺度混沌免疫算法優化FLS-SVM參數，從而建立IFLS-SVM分類辨識模型。

1.1 模糊最小二乘支持向量機

一般地，令模糊最小二乘支持向量機的輸入模糊樣本為

(1,1,(1))，…，(x,y,(x))，…，

(x,y,(x))，=1，2，…，。

式中：x為輸入變量；y為輸出變量；(x)為隸屬度，0≤(x)≤1。模糊最小二乘支持向量機的最優分類面為式(1)所示的目標函數的最優解[15]：

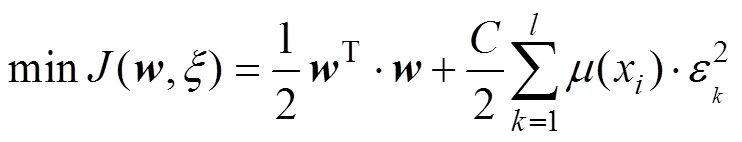
s.t.y=T?(x)++ε；ε＞0；=1，2，…，

式中：ε為松弛變量；為懲罰因子；為閾值。

相應的拉格朗日函數為

式中：a為拉格朗日系數。則模糊最小二乘支持向量機優化問題轉化為求解線性方程：

式中：=[1，…，，…，y]T；=[1，…，1，…，1，l]T；=[1，…，，…，a]T；=(x)?(x)=(x,x)；=1，2，…，。

FLS-SVM分類辨識模型如圖1所示，則該分類辨識模型為

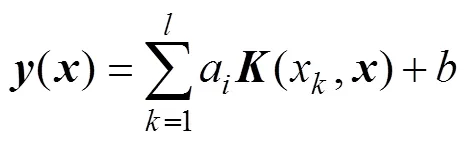
式中：x=[x1，…，xk，…，xl]；K(xk, x)=exp{-|xk-x|2/σ2}；σ為核參數。

1.2 FLS-SVM的隸屬度確定

采用如圖2所示的三角形隸屬度函數法確定分類指標的隸屬度，其計算公式為[19]

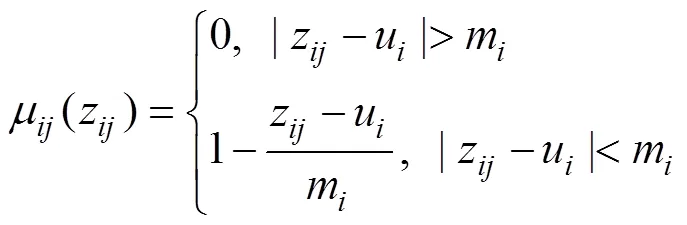
式中：為第個分類指標的第次實際值；為第個分類指標實際值的均值；為第個分類指標的模糊子集的邊界，是用來確定第個分類指標隸屬度的必要條件，可以根據實際應用情況進行自適應調整，一般取=2；為第個分類指標的相應實際值的方差，

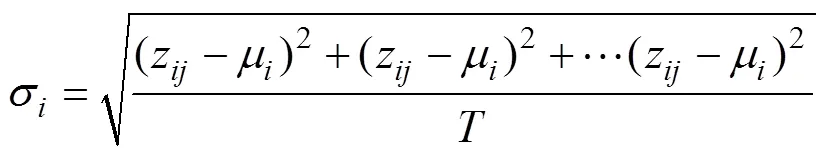
為總樣本數。

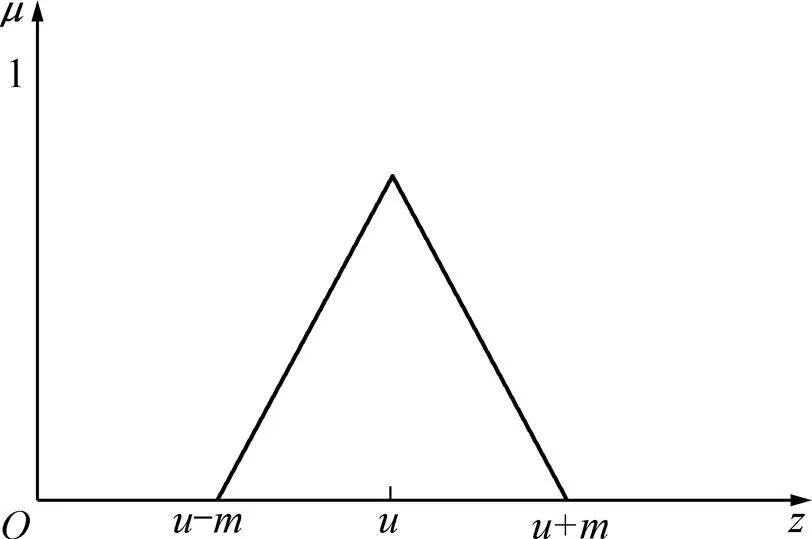
圖2 三角形隸屬函數

1.3 FLS-SVM的參數優化

應用FLS-SVM分類辨識模型進行分類辨識時，正則化參數和核參數的選擇是一個重要問題。為此，采用自適應變尺度混沌免疫算法對FLS-SVM的正則化參數和核參數進行優化時，可由下式確定自適應變尺度混沌免疫算法的適應度函數：

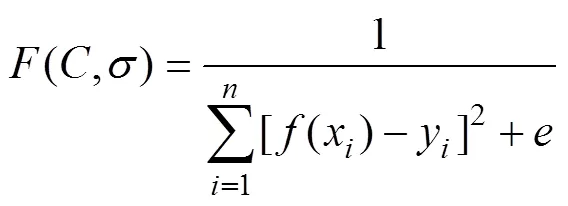
式中：y為期望輸出；(x)為實際輸出；為1個很小的實數，其作用是防止分母出現0的情況，此處為10?3。定義誤差函數MS作為FLS-SVM泛化性能的評價指標：

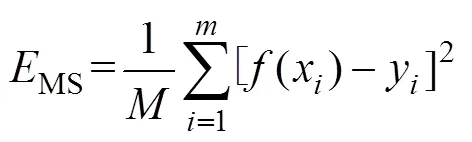
式中：(x)為實際輸出；y為期望輸出。

自適應變尺度混沌免疫算法優化FLS-SVM參數的具體步驟如下。

Step 1 將=[1，…，，…，x]作為抗原{A}輸入，并進行標準化處理。選擇+1=4(1?)作為混沌模型在目標函數定義域內隨機產生個初始化抗體{A}的混沌變量。

Step 2 對每個抗原A操作如下。

Step 2.1 利用式(9)分別計算每個抗體A與抗原A的親和力β，

Step 2.2 選擇個親和力最強的抗體作為網絡細胞，并對其進行克隆操作，得到相應的克隆數c。

Step 2.3 對第次克隆后的細胞應用方程C(z+1)=C?(C?X)進行變異操作(其中，C為第次克隆抗體細胞數，X為第次克隆抗原細胞數，為變異率)。

Step 2.4 計算第次變異操作后的克隆抗體細胞數C(z+1)和第?1次變異操作后的克隆抗體細胞數C的親和力。

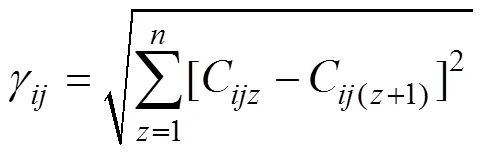
Step 2.5 選擇親和力最強的25%的克隆抗體細胞作為記憶細胞數據集p。

Step 2.6 利用式(11)計算每個抗體A同抗體A間相似度λ，淘汰記憶細胞數據集p中相似度λ大于閾值s的個體。

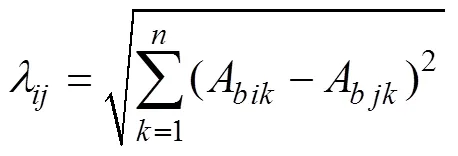
Step 3 將淘汰完畢的記憶細胞數據集p合并到記憶數據集中。

Step 4 對較優個體進行混沌搜索。

選擇記憶庫中適應值較大的15%的個體進行混沌細搜索。設較優個體為=(1，…，，…，X)，混沌變量搜索區間的縮小表示為

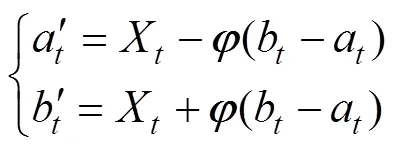
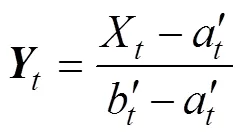
將與的非線性組合作為新的混沌變量，用此混沌變量進行搜索。

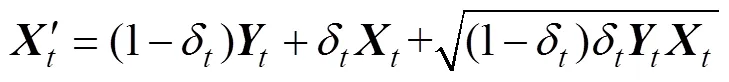
式中：δ為自適應調節系數，0＜δ＜1。自適應調節系數δ采用下式進行自適應確定：

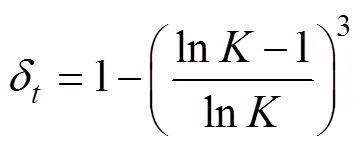
式中：為進化代數。淘汰記憶庫中適應值較大的8%的個體相似度大于s的個體。

Step 5 選擇+1=4(1?)作為產生′個(0, 1)間的個體，替換親和力差的個體，與上次免疫計算得到的記憶數據集作為下一代免疫計算的抗體，并返回Step 2，直到達到網絡收斂為止。

Step 6 用適應度函數評價*，計算相應的(*)。若(*)>()，則()=(*)，否則放棄*。

Step 7 若滿足截止判據MS＜10?5，則截止搜索，輸出最優解，否則返回Step 1。

1.4 IFLS-SVM分類辨識效果仿真驗證

為驗證IFLS-SVM分類辨識模型的分類辨識效果，用3個常用標準測試(UCI)數據集進行實驗，并與LS-SVM分類辨識模型和FLS-SVM分類辨識模型相 比較。

1) Ripley數據集。采用第2類Ripley數據集，其中訓練集含300個樣本(其中正負類各150個)，測試集1 000個樣本(正負類各500個)。

2) MONK數據集。采用含有隨機添加的噪聲點的第3類MONK數據集，訓練集含130個樣本(其中正、負類分別為65個和65個)，測試集440個樣本(其中、正負類分別為230個和210個)。

3) PIMA數據集。PIMA數據集總樣本為800個(其中正、負類分別為500個和300個)。在數據集文件中隨機選取600個樣本訓練，剩余200個樣本測試。

對3個常用標準測試(UCI)數據集中數據進行歸一化處理，并采用LS-SVM分類辨識模型、FLS-SVM分類辨識模型和本文中提出的IFLS-SVM分類辨識模型對其進行辨識分類，這3種方法得到的最優測試精度及達到最優測試精度時所對應的參數分別見表1和表2。從表1可以看出：本文提出的IFLS-SVM分類辨識模型能夠有效提高帶噪聲點和異常點數據集數據的分類辨識精度。

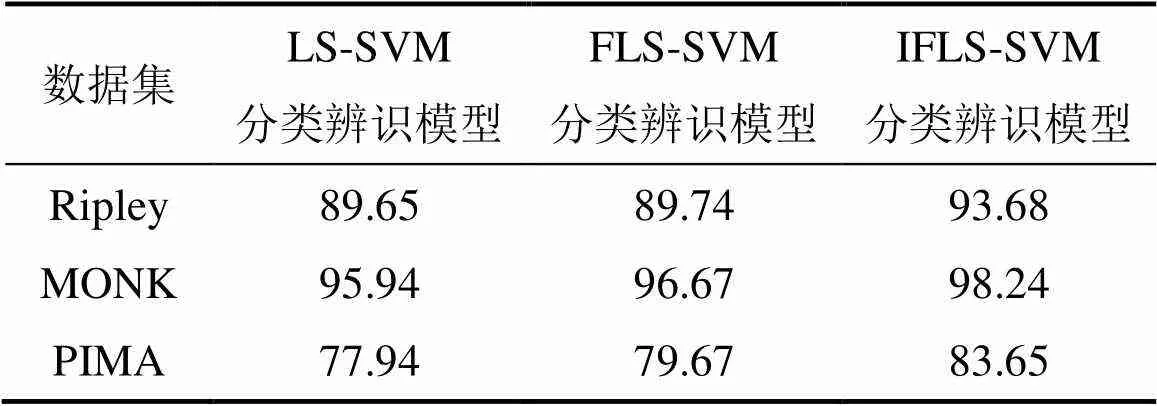
表1 最優辨析精度

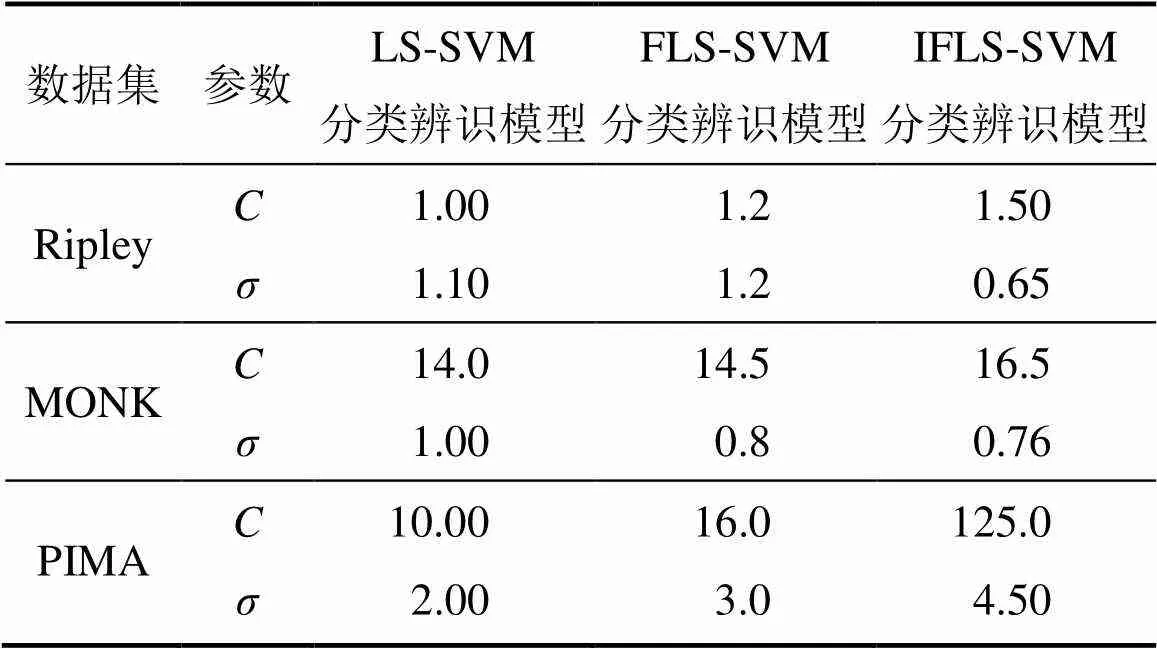
表2 最優分類辨識精度時對應參數

基于CPU的3種分類辨識模型計算耗時見表3。由表3可知：LS-SVM分類辨識模型和FLS-SVM分類辨識模型的CPU計算耗時較多，而IFLS-SVM分類辨識模型的CPU計算耗時最少。

表3 3種分類器的CPU計算耗時對比

2 IFLS-SVM分類辨識模型的實際應用

2.1 在地下金屬礦山采場信號分類辨識中的應用

圖3所示為南方某地下金屬礦山開采過程中采集的機械振動、爆破信號和采場圍巖聲發射信號測試結果，且各為600組。

從地下金屬礦山采場圍巖聲發射信號及干擾信號數據中取150個有效樣本數據，75個為訓練集(巖石破裂信號25個、機械振動信號25個和聲發射信號25個)，75個為樣本測試集(巖石破裂信號25個、機械振動信號25個和聲發射信號25個)，分別采用LS-SVM分類辨識模型、FLS-SVM分類辨識模型和IFLS-SVM分類辨識模型對地下金屬礦山采場圍巖聲發射信號及干擾信號測試數據進行分類，其結果如表4所示。從表4可知：采用LS-SVM分類辨識模型、FLS-SVM分類辨識模型和IFLS-SVM分類辨識模型的分類精度分別為82.67%，86.67%和90.67%。可見IFLS-SVM分類辨識模型由于在構造適應度函數時，將模糊分類有效性指標和模糊分類正確樣本數為適應度函數的子目標，從而使得不同的樣本有不同的貢獻，在較大程度上減弱了噪聲和孤立點對分類的影響，使學習算法在代價敏感數據或含噪聲數據的情況下更加具有穩健性。

2.2 在中國國際貿易安全分類辨識中的應用

2.2.1 中國國際貿易安全評價指標

針對中國國際貿易實際情況，選擇易于獲取、操作性強并且最能客觀反映中國國際貿易安全現狀的指標，即固定資產投資總額1、實際利用外資金額2、城鄉居民儲蓄存款年底余額3、外匯儲備4、人民幣對美元匯率5和貨幣供應量6。

(a) 巖石破裂信號；(b) 機械振動信號；(c) 聲發射信號

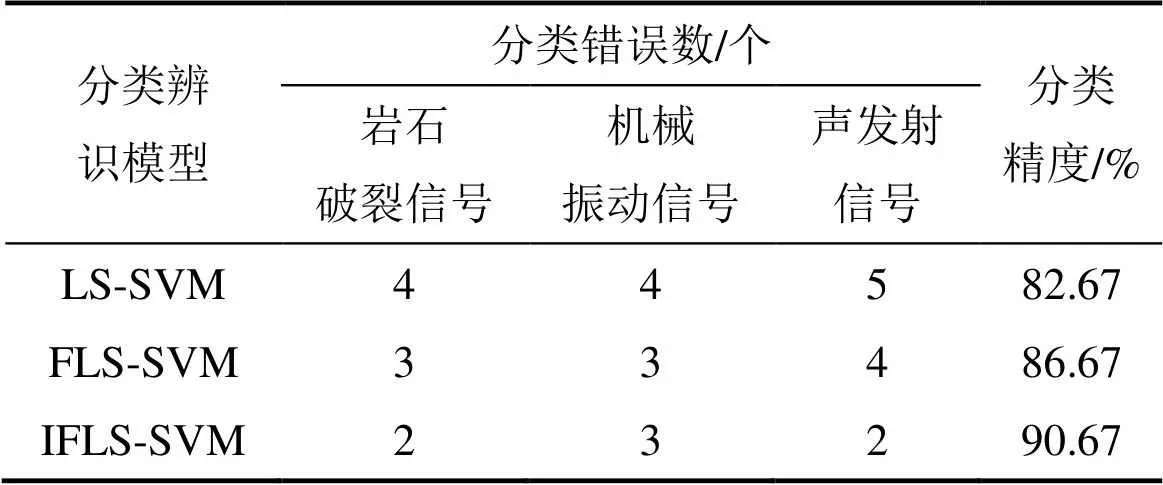
表4 測試數據分類結果

2.2.2 中國國際貿易安全性等級劃分

IFLS-SVM分類辨識模型輸出參數為中國國際貿易安全性等級，分為5級，IFLS-SVM分類辨識模型期望輸出的5級的值依次為：A級(極不安全)，1=(l，0，0，0，0)；B級(較不安全)，2=(0，1，0，0，0)；C級(一般安全)，3=(0，0，l，0，0)；D級(較安全)，4=(0，0，0，l，0)；E級(極安全)，5=(0，0，0，0，1)。因此，IFLS-SVM分類辨識模型輸出參數為中國國際貿易安全性等級值R(=1，2，3，4，5)。

2.2.3 中國國際貿易安全性分類辨識

1980—2014年中國國際貿易安全性分類指標參數如表5所示[20]。以1980—2006年參數作為訓練樣本集，以2007—2014年參數作為測試樣本，進行中國國際貿易安全性分類辨識。由于歷史資料不夠全面及不夠準確，給專家判斷中國國際貿易安全性R分類帶來一定影響，因此，專家只能根據歷史進出口貿易總值給出1980—2014年中國國際貿易安全性R的模糊判斷，如表5所示。

為驗證IFLS-SVM分類辨識模型(用模型F2表示)的有效性，用表5所示數據進行仿真實驗，并與文獻[10]中的分類器(用模型F1表示)分類結果進行比較。

采用式(5)和式(6)求得表5中中國國際貿易安全性指標，即1，2，3，4，5和6的隸屬度，以中國國際貿易安全性R(=1，2，…，5)作為IFLS-SVM分類辨識模型的輸出，以1980—2006年的1，2，3，4，5和6作為模糊最小二乘支持向量機的輸入，借助于建立的IFLS-SVM分類辨識模型，可得1980—2006年中國國際貿易安全性的辨析值和實際值，如表6所示。從表6可見：模型F2的辨析值與實際值的相對誤差小于0.70%，具有較高的預測精度。

以中國機電產品出口貿易風險R(=1，2，…，5)作為IFLS-SVM分類辨識模型的輸出，以2007—2014年的1，2，3，4，5和6作為IFLS-SVM分類辨識模型的輸入，借助于已經訓練好的中國機電產品出口貿易風險智能預警分析模型，可得到2007—2014年的中國機電產品出口貿易風險的智能預警分析值和實際值如表7所示，模型F2的辨析值和實際值相對誤差小于0.90%，表明IFLS-SVM具有較高的預測精度。

以IFLS-SVM分類辨識模型輸出對輸入分量的偏導數γ作為影響因子對中國國際貿易安全性影響程度的判據，偏導數愈大，則說明該因子的影響作用愈顯著，各指標參數對中國國際貿易安全性的影響因子計算結果如圖4所示。由圖4可知：固定資產投資總額的影響因子1＞貨幣供應量影響因子6＞人民幣對美元匯率影響因子5＞實際利用外資金額影響因子2＞外匯儲備影響因子4＞城鄉居民儲蓄存款年底余額影響因子3。可見，對中國國際貿易安全性影響程度由大至小依次是1，6，5，2，4和3。其原因可能是：固定資產投資總額的增長能較大程度地促進中國國際貿易的發展，國內固定資產投資總額越大，越能刺激出口貿易增長，對中國國際貿易安全的影響也就越大。貨幣供應量可有效促進國內市場需求，從而在一定程度上促進進出口貿易增長，也會對中國國際貿易安全帶來較大影響。人民幣對美元匯率的影響不如固定資產投資總額1、貨幣供應量6的影響顯著，其主要原因是人民幣對美元匯率的變化會導致出口需求的變化，即對出口市場需重新選擇，對美元升值可能會導致對貶值地區的出口量增加，因此，對中國國際貿易安全的變化影響不顯著。

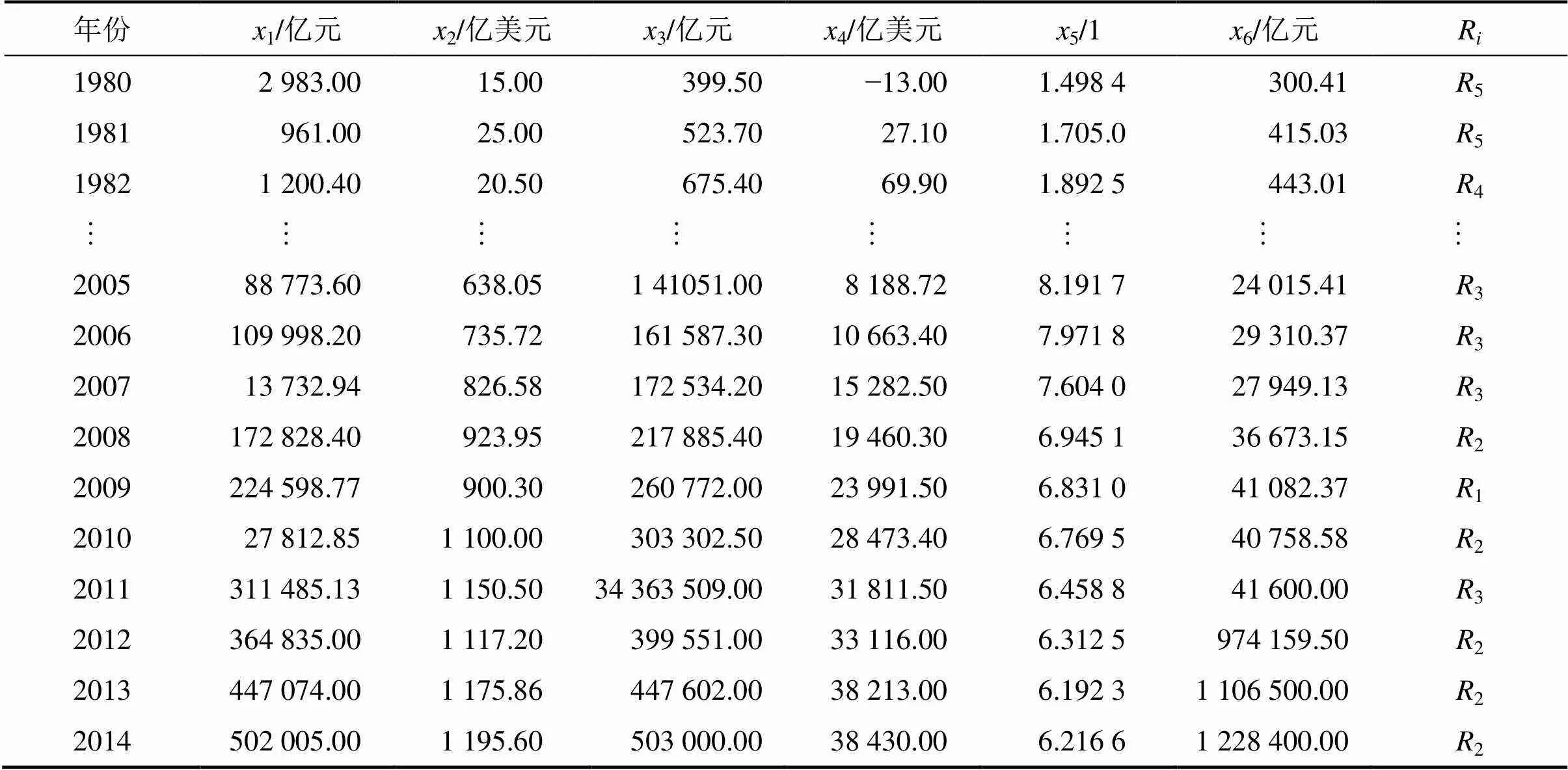
表5 中國國際貿易安全性指標參數xi

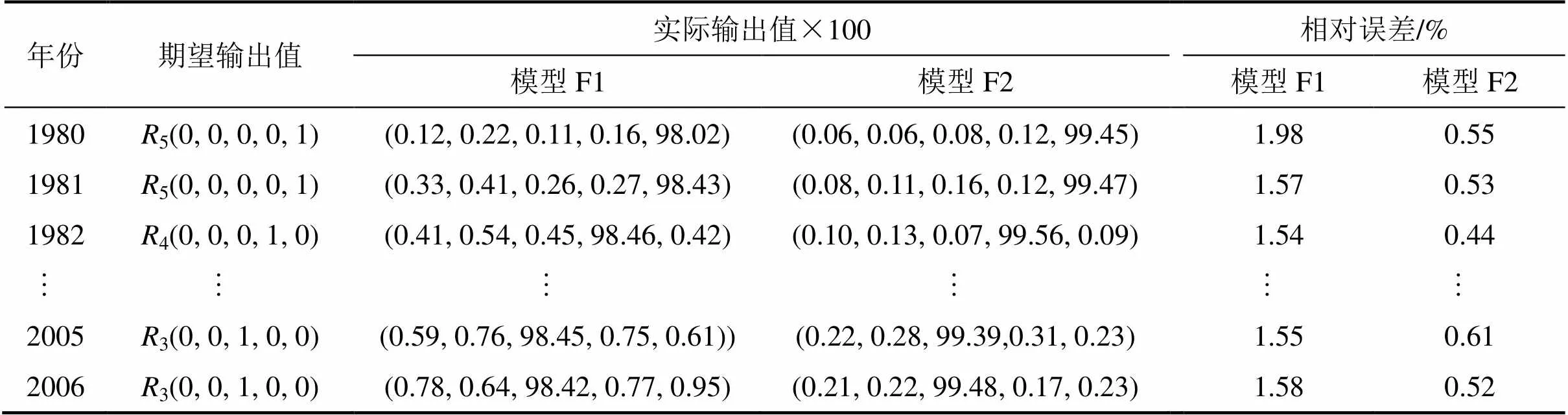
表6 基于中國國家貿易參數的IFLS-SVM分類辨識模型訓練結果

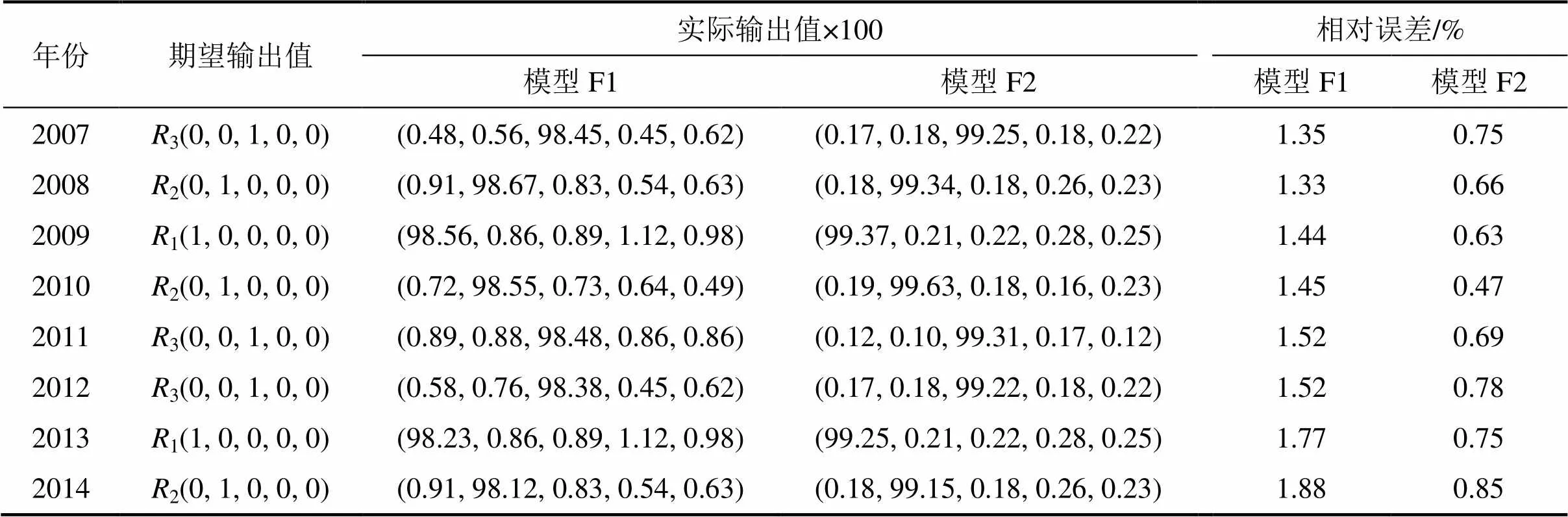
表7 訓練后IFLS-SVM分類辨識模型測試結果

從1980—2014年中國國際貿易性辨析仿真分析實例可看出IFLS-SVM分類辨識模型具有很大的優勢，為中國國際貿易安全性準確辨析提供了一種有效的解決方法。

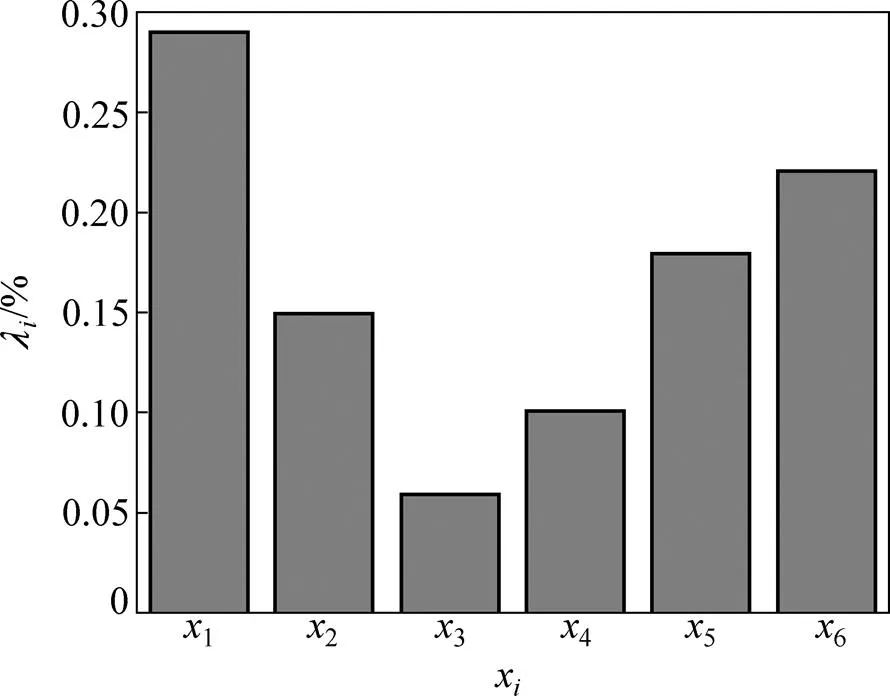
圖4 中國國際貿易安全性指標參數影響因子

3 結論

1) 針對分類辨識數據的模糊特性，采用三角形隸屬度函數法確定模糊最小二乘支持向量機隸屬度，采用自適應變尺度混沌免疫算法優化FLS-SVM的參數，從而建立了IFLS-SVM分類辨識模型。IFLS-SVM分類辨識模型能夠有效提高帶噪聲點和異常點數據集數據的辨析精度，其智能辨析相對誤差小于0.8%，具有較高的預測精度。

2) LS-SVM分類辨識模型、FLS-SVM分類辨識模型和IFLS-SVM分類辨識模型的分類精度分別為82.67%，86.67%和90.67%。

3) 對中國國際貿易安全性影響由大至小依次是固定資產投資總額1、貨幣供應量6、人民幣對美元匯率5、實際利用外資金額2、外匯儲備4和城鄉居民儲蓄存款年底余額3。

[1] MONTEIRO R V A, GUIMAR?ES G C, MOURA F A M, et al. Estimating photovoltaic power generation: performance analysis of artificial neural networks, support vector machine and Kalman filter[J]. Electric Power Systems Research, 2017, 143: 643?656.

[2] COUELLAN N, WANG Wenjuan. Uncertainty-safe large scale support vector machines[J]. Computational Statistics & Data Analysis, 2017, 109: 215?230.

[3] ABD A M, ABD S M. Modelling the strength of lightweight foamed concrete using support vector machine(SVM)[J]. Case Studies in Construction Materials, 2017, 6: 8?15.

[4] LIU Chuan, WANG Wenyong, WANG Meng, et al. An efficient instance selection algorithm to reconstruct training set for support vector machine[J]. Knowledge-Based Systems, 2017, 116: 58?73.

[5] ZHANG Jun, OU Jianping, ZHAN Ronghui.Automatic target recognition of moving target based on empirical mode decomposition and genetic algorithm support vector[J]. Journal of Central South University, 2015, 22(4): 1389?1396.

[6] CARRIZOSA E, NOGALES-GóMEZ A, MORALES D R. Clustering categories in support vector machines[J]. Omega, 2017, 66(Part A): 28?37.

[7] WANG Di, ZHANG Xiaoqin, FAN Mingyu, et al. Hierarchical mixing linear support vector machines for nonlinear classification[J]. Pattern Recognition, 2016, 59: 255?267.

[8] HANG Jun, ZHANG Jianzhong, CHENG Ming. Application of multi-class fuzzy support vector machine classifier for fault diagnosis of wind turbine[J]. Fuzzy Sets and Systems, 2016, 297: 128?140.

[9] ABE S. Fuzzy support vector machines for multilabel classification[J]. Pattern Recognition,2015, 48(6): 2110?2117.

[10] ?OMAK E, POLAT K, GüNE? S, et al. A new medical decision making system: Least square support vector machine (LSSVM) with fuzzy weighting pre-processing[J]. Expert Systems with Applications, 2007, 32(2): 409?414

[11] WANG Chunpeng, WANG Xingyuan, ZHANG Chuan, et al. Geometric correction based color image watermarking using fuzzy least squares support vector machine and Bessel K form distribution[J]. Signal Processing, 2017, 134: 197?208.

[12] 王志強, 李立君, 黃雁, 等. 基于模糊最小二乘支持向量機的火災信號辨識[J]. 中南大學學報(自然科學版), 2013, 44(1): 202?207. WANG Zhiqiang, LI Lijun, HUANG Yan, et al. Fire disaster signal recognition based on fuzzy least squares support vector machines[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 202?207.

[13] 李巖波, 張超, 郭新辰. 基于直覺模糊最小二乘支持向量機的變壓器故障診斷[J]. 吉林大學學報(理學版), 2014, 52(2): 313?318.LI Yanbo, ZHANG Chao, GUO Xinchen. Transformer fault diagnosis based on intuitionistic fuzzy least squares support vector machine[J]. Journal of Jilin University (Science Edition), 2014, 52(2): 313?318.

[14] ZUO Hongyan, LUO Zhouquan, GUAN Jialin, et al. Identification on rock and soil parameters for vibration drilling rock in metal mine based on fuzzy least square support vector machine[J]. Journal of Central South University, 2014, 21(3): 1085?1090.

[15] WANG Taosheng, ZUO Hongyan. Fuzzy least squares support vector machines soft measurement model based on adaptive mutative scale chaos immune algorithm[J]. Journal of Central South University, 2014, 21(2): 593?599.

[16] VAPNIK V. Statistical learning theory[M]. New York: Wiley, 1998: 30?55.

[17] 鄂加強. 智能故障診斷及其應用[M]. 長沙: 湖南大學出版社, 2006: 100?145. E Jiaqiang. Intelligent fault diagnosis and its application[M]. Changsha: Hunan University Press, 2006: 100?145.

[18] 彭海仔. 基于T-S模糊模型的太陽位置算法[J]. 上海海事大學學報, 2014, 35(2): 81?84. PENG Haizai. Sun position algorithm based on T-S fuzzy model[J]. Journal of Shanghai Maritime University, 2014, 35(2): 81?84.

[19] 羅周全, 左紅艷, 王益偉. 人?機?環境系統安全性的模糊熵評價方法[J]. 模糊系統與數學, 2011, 25(6): 169?174. LUO Zhouquan, ZUO Hongyan, WANG Yiwei. Fuzzy entropy evaluation method of the safety for man?machine?environment system[J]. Fuzzy Systems and Mathematics, 2011, 25(6): 169?174.

[20] 左紅艷. 機電產品出口貿易復雜性分析及其風險預警預報研究[M]. 長沙: 中南大學出版社, 2015: 140?141. ZUO Hongyan. Study on the complexity of the export trade of electromechanical products and its risk prediction[M]. Changsha: Central South University Press, 2015: 140?141.

(編輯 陳燦華)

An improved FLS-SVM classification identification model and its application

ZUO Hongyan1, 2, WANG Taosheng2

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. School of Business, Hunan International Economics University, Changsha 410205, China)

A classification and identification model was developed based on improved fuzzy least squares support vector machines(FLS-SVM),in which the fuzzy membership function was set by using triangle function method and its parameters were optimized by an adaptive mutative scale chaos immune algorithm, and an improved fuzzy least squares support vector machines(IFLS-SVM) was constructed. The simulation experiments were conducted on three benchmarking datasets such as Ripley datasets, MONK datasets and PIMA datasets for testing the generalization performance of the classification and identification model, signals from underground metal mines stope wall rock and international trade data in China were diagnosed by the IFLS-SVM classification and identification model. The results show that compared with LS-SVM classification identification model and FLS-SVM classification identification model, the IFLS-SVM classification identification model is valid for improving the analysis accuracy of the data with noises or outliers and IFLS-SVM classification identification model has small relative error.

chaos immune algorithm; fuzzy support vector machines; classification identification

10.11817/j.issn.1672?7207.2017.08.017

TP183

A

1672?7207(2017)08?2097?08

2016?12?18；

2017?02?21

國家自然科學基金資助項目(71573082)；湖南省自然科學基金資助項目(2017JJ2134)；湖南省高校創新平臺開放基金資助項目(14K055)(Project(71573082) supported by the National Natural Science Foundation of China; Project(2017JJ2134) supported by the Natural Science Foundation of Hunan Province; Project(14K055) supported by the Innovation Platform Open Fund of Hunan Province)

左紅艷，博士(后)，講師，從事人工智能和非線性科學融合理論及其在國際貿易中的研究；E-mail：zuohongyan18@126.com