注重變式訓(xùn)練 提升思維品質(zhì)

江蘇省盱眙縣第一中學(xué) 路國躍

注重變式訓(xùn)練 提升思維品質(zhì)

江蘇省盱眙縣第一中學(xué) 路國躍

課堂教學(xué)可分為三類：新授課、習(xí)題課、復(fù)習(xí)課，其中習(xí)題課、復(fù)習(xí)課較為難上，因?yàn)闆]有新授知識點(diǎn)，照題講題會使學(xué)生有乏味感，尤其對于優(yōu)秀學(xué)生。筆者結(jié)合自己教學(xué)和聽課情況，發(fā)現(xiàn)課堂中此類問題比較嚴(yán)重，促使筆者反思：如何改進(jìn)才能提高教學(xué)效果，提升學(xué)生的思維品質(zhì)？復(fù)習(xí)課不能一味地解題，讓學(xué)生機(jī)械化地進(jìn)行訓(xùn)練，在解題的同時也要進(jìn)行變式。“變式訓(xùn)練”既能吸引學(xué)生注意力，扣住學(xué)生的心弦，又能使學(xué)生解題思路開闊，培養(yǎng)學(xué)生勇于探索的精神，克服死搬硬套的毛病，從而培養(yǎng)學(xué)生的創(chuàng)新能力。

課堂教學(xué)是一線教師展示教學(xué)能力的舞臺，也是教師反思教學(xué)問題、改進(jìn)教學(xué)能力的場所。現(xiàn)將自己在習(xí)題課中如何變式補(bǔ)充，抓住學(xué)生興趣，提升學(xué)生課堂思維能力的做法整理出來。

一、基于原題，激發(fā)思考

例1 如圖1，點(diǎn)A為反比例函數(shù)圖像上一點(diǎn)，過A作AB⊥x軸于點(diǎn)B，連接OA，△ABO的面積為3，則反比例函數(shù)的關(guān)系式為 _________ 。

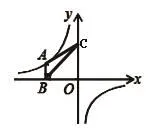
圖1

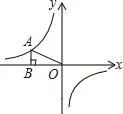
圖2

變式題：如圖2，點(diǎn)A在反比例函數(shù)圖像上，AB垂直y軸于點(diǎn)B，點(diǎn)C為y軸上任意一點(diǎn)，且△ABC的面積為2，則這個反比例函數(shù)的解析式為________ 。

變式意圖：題目沒有直接告訴學(xué)生常規(guī)的直角三角形面積，迫使學(xué)生根據(jù)條件重構(gòu)符合要求的直角三角形。怎么構(gòu)造？這里就自然而然地產(chǎn)生了數(shù)學(xué)思維，誘發(fā)學(xué)生思考，激發(fā)課堂活力。方法是：連接OA，根據(jù)AB∥OC，可得S△AOB=S△ABC=2，從而解決問題。

二、因果互換，強(qiáng)化解題能力

圖3

圖4

變式題：如圖4所示，原題條件不變。若點(diǎn)P是y軸上一點(diǎn)，△ABP的面積是6，請求出點(diǎn)P的坐標(biāo)。

變式意圖：將原題中的條件與結(jié)果互換，這是老師變式的常用手段。原點(diǎn)O類似于變式題的點(diǎn)P，原題中的△AOB類似于變式后的△ABP。要想求出點(diǎn)P坐標(biāo)，就必須將面積向邊轉(zhuǎn)化。促使學(xué)生畫出草圖，將△ABP分割成△APM和△BPM，利用面積及A、B點(diǎn)的橫坐標(biāo)求出MP的長度，從而解出點(diǎn)P坐標(biāo)有2個。變式題的解題思路和原題是一致的，用割補(bǔ)法分割原三角形面積，但難度上升，又是逆向思考，能有效激發(fā)學(xué)生思考，產(chǎn)生數(shù)學(xué)思維。

三、重構(gòu)情景，提升數(shù)學(xué)思維

例3 矩形ABCD在坐標(biāo)系中如圖5所示放置。已知點(diǎn)B、C在x軸上，點(diǎn)A在第二象限，D（2，4），BC=6，反比例函數(shù)（x＜0）的圖象經(jīng)過點(diǎn)A。求k值。

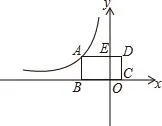
圖5

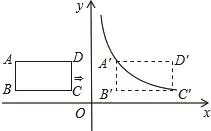
圖6

變式題：如圖6，在平面直角坐標(biāo)系中，四邊形ABCD是矩形，AD∥x軸，A（-，3），AB=2，AD=3。（1）直接寫出B、C、D三點(diǎn)的坐標(biāo)；（2）將矩形ABCD向右平移m個單位，使點(diǎn)A、C恰好同時落在反比例函數(shù)（x＞0）的圖象上，得到矩形A'B'C'D'。求矩形ABCD的平移距離m和反比例函數(shù)的解析式。

變式意圖：原題可以根據(jù)條件直接求出點(diǎn)A坐標(biāo)，從而求出反比例函數(shù)。變式題一改常態(tài)，點(diǎn)A＇、C＇坐標(biāo)都不可直接求出，看似常規(guī)方法無計可施，但兩點(diǎn)坐標(biāo)都可以用m表示，A＇（-，3）、C＇（-），將表示好的坐標(biāo)一起代入，即可求出m和k。或者利用xy=k，得到3（-）=-，依次求出k、m。變式題能有效鞏固學(xué)生對待定系數(shù)法的理解，更能激發(fā)學(xué)生的探索欲望，緊緊拴住學(xué)生的心。

四、設(shè)置難點(diǎn)，激發(fā)探索

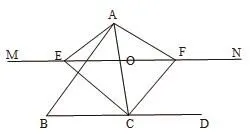
圖7

圖8

例4 如圖7，在△ABC中，點(diǎn)O是AC邊上一動點(diǎn)， 過點(diǎn)O作直線MN∥BC，設(shè)MN交∠BCA的平分線于點(diǎn)E，交∠BCA的外角平分線于點(diǎn)F。（1）說明EO＝FO；（2）當(dāng)點(diǎn)O運(yùn)動到何處時，四邊形AECF是矩形？證明你的結(jié)論。

變式題：如圖8，正方形ABCO的邊OA、OC在坐標(biāo)軸上，點(diǎn)B坐標(biāo)為（6，6），將正方形OCBA繞點(diǎn)C逆時針旋轉(zhuǎn)一個銳角度數(shù)α，得到正方形DCFE，ED交線段AB于點(diǎn)G，ED的延長線交線段OA于點(diǎn)H，連接CH、CG。（1）求證：△CBG≌△CDG；（2）直接寫出∠HCG=___ ，HG、OH、BG之間的數(shù)量關(guān)系為_____ 。（3）連接BD、DA、AE、EB得到四邊形AEBD，在旋轉(zhuǎn)過程中四邊形AEBD能否為矩形？如果能，請求出點(diǎn)H的坐標(biāo)；如果不能，請說明理由。

變式意圖：原題的（2）問是很常規(guī)的矩形證明題，對于優(yōu)生問題不大。若課堂有時間，或者留給學(xué)有余力的學(xué)生課后探索，變式題是一個很有質(zhì)量的題目。難度在于（3）問，矩形要成立，則需滿足對角線相等且相互平分，從而推出DG=AG==3。設(shè)OH=HD=x，進(jìn)而在Rt△AGH中用勾股定理解決問題。

總之，在數(shù)學(xué)教學(xué)過程中積極運(yùn)用“變式訓(xùn)練”教學(xué)，不僅能讓學(xué)生在學(xué)習(xí)中收獲快樂、體驗(yàn)成功，還能培養(yǎng)學(xué)生獨(dú)立思考、不斷創(chuàng)新的能力。因此教師要在原題目基礎(chǔ)上通過變換、類比、引申等方式，拓展問題的條件或設(shè)問的方式，以期達(dá)到變式效果，為學(xué)生的思維能力，也為教師自身的教學(xué)能力奠定基礎(chǔ)。

[1]季燕．善于變式，方能變通[J]．考試周刊，2014（76）．

[2]石鳳芹．在數(shù)學(xué)教學(xué)中培養(yǎng)發(fā)散思維能力[J]．現(xiàn)代教育科學(xué)：中學(xué)教師，2011（7）．