合理表示“等可能事件”的所有結果

潘 霞

合理表示“等可能事件”的所有結果

潘 霞

概率是研究不確定現象的數學模型.同學們通過對“等可能條件下的概率”的學習，得到了等可能條件下的概率的計算公式：

一般地，如果一個試驗有n個等可能的結果，當其中的m個結果之一出現時，事件A發生，那么事件A發生的概率P（A）可以表示為：

該公式的應用僅限于試驗的所有可能出現的結果是有限的，且是等可能的.那么列出試驗的所有等可能出現的結果成為解決問題的關鍵.

一、方法多樣

例1（蘇科版《數學》教材九年級上冊第133頁“思考與探索”）拋擲一枚質地均勻的硬幣2次，2次拋擲的結果都是正面朝上的概率是多少？

【分析】可以用直接分類列舉的方法，也就是我們熟悉的枚舉法列出所有等可能出現的結果.

【方法一】列舉出所有等可能出現的結果：（正，正），（正，反），（反，正），（反，反），再利用等可能條件下的概率計算公式求其概率.

【分析】為了避免在直接列舉的過程中重復或遺漏，可借助表格或樹狀圖列出拋擲一枚質地均勻的硬幣2次所有可能出現的結果.

【方法二】表格：

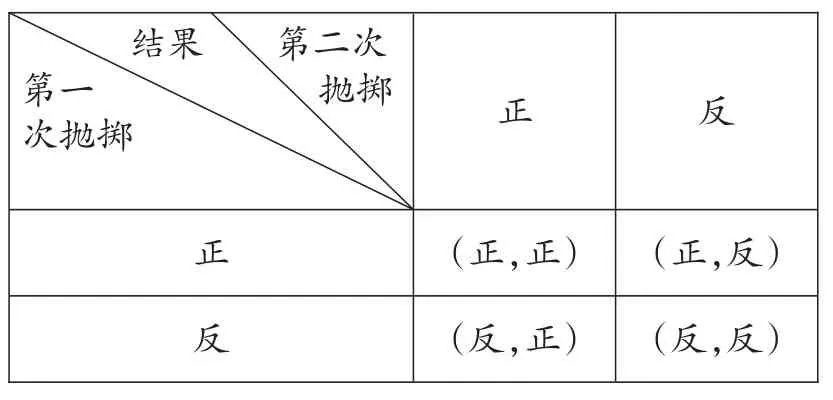
共有4種可能出現的結果，并且它們都是等可能的“.2次拋擲的結果都是正面朝上”記為事件A，它的發生只有一種可能，所以事件A發生的概率P（A）=，即2次拋擲的結果都是正面朝上的概率是

【方法三】樹狀圖：

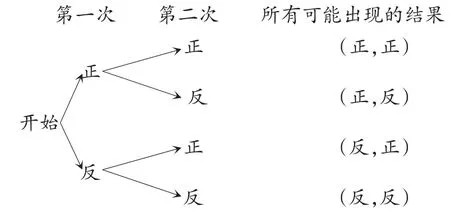
（同表格求解）

【點評】等可能出現的結果是有限的且易于分類，這種等可能條件下的概率問題，我們都可以借助表格、樹狀圖將所有結果無重復無遺漏地表示出來，并且具有直觀性，實際上這兩種方法是枚舉法的升級版.

這兩種方法哪種更合理，更有效？它們各有怎樣的特點？在使用的時候又需要注意什么問題？

二、方法優化

在例1中，試驗分為2步，并且所有等可能出現的結果數較少，運用表格和樹狀圖求解都比較有效.

例2 若將例1問題中的試驗工具硬幣改為骰子，兩次拋擲骰子點數和為5的概率是多少？

【分析】與拋擲硬幣相同，都屬于等可能條件下的概率問題，那么我們是選擇表格還是樹狀圖來表示所有等可能出現的結果呢？若選擇樹狀圖，第一次有六種結果，第二次也有六種結果，也就是共有36種結果數，這是棵枝繁葉茂的樹，顯然用樹狀圖表示，結果不夠清晰.表格就不同了，同學們可以動筆試試哦！

【點評】當試驗分2步，但所有等可能出現的結果數較多時，運用表格分析則顯得較為清晰、便捷.

例3 拋擲一枚質地均勻的硬幣3次，3次拋擲的結果都是正面朝上的概率是多少？

【分析】若用表格求解，得到一個三維的立體表格，而這在二維平面上表示出來是比較困難的，又或者列兩個表格，也較為煩瑣.

【點評】當試驗分為3步時，則一般運用“樹狀圖”列出所有等可能出現的結果.

“有放回無放回試驗”在用表格和樹狀圖表示結果數時要注意什么？同學們你們清楚嗎？

三、靈活運用

例4 一個不透明的袋子中有大小、質地完全相同的4只小球，小球上分別標有1、2、3、4四個數字.

（1）從袋中隨機摸出一只小球，求小球上所標數字為奇數的概率；

（2）從袋中隨機摸出一只小球，再從剩下的小球中隨機摸出一只小球，求兩次摸出的小球上所標數字之和為5的概率.

【分析】第（2）問說明試驗有2步，第1步是從4只小球中隨機摸1只，而第2步是從剩下的小球，也就是3只小球中隨機摸1只，是“無放回的摸球游戲”.所以在解答時要謹慎對待.

解：方法一（列表法）：

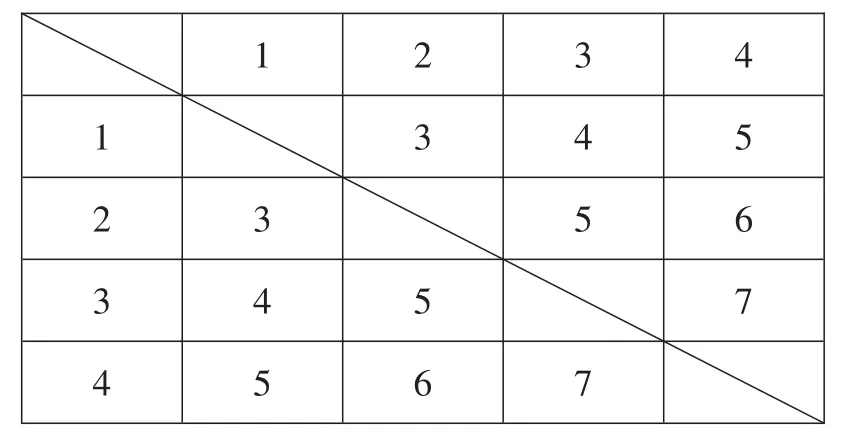
共有12種等可能的結果，其中兩次摸出的小球上所標數字之和為5的可能性有4種，所以P（兩次摸出的小球數字之和為5）

方法二（樹狀圖）：

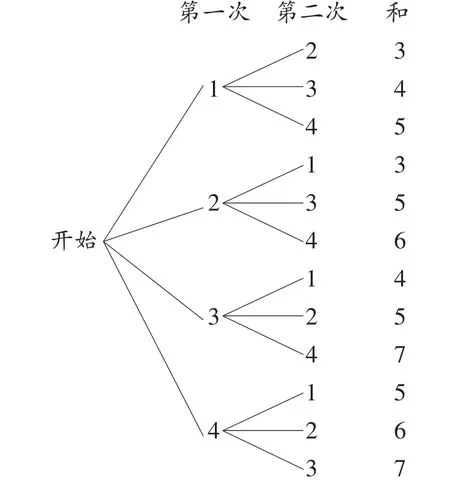
共有12種等可能的結果，其中兩次摸出的小球上所標數字之和為5的可能性有4種，所以P（兩次摸出的小球數字之和為5）

不管用哪種方法表示試驗結果數，它們只是解決問題的工具.哪種方法更合理，需要抓住問題的本質去判斷.當然這些解決概率問題的方法只是九牛一毛，隨著學習的深入，概率將作為一門獨立的學科，等待我們去探究，去發現.

（作者單位：江蘇省常州市金壇區白塔中學）