航空復合材料孔隙率的超聲波衰減法檢測

， ，，，,

(1.北京理工大學珠海學院，數理與土木工程學院，珠海 519088;2.中航通飛華南飛機工業有限公司，珠海 519088)

航空復合材料孔隙率的超聲波衰減法檢測

沈洋1，游泳1，郭治文2，張國才1，邢秀文1,謝小榮1

(1.北京理工大學珠海學院，數理與土木工程學院，珠海519088;2.中航通飛華南飛機工業有限公司，珠海519088)

以國內自主研制的首款全機身復合材料某型號飛機使用的復合材料板試件為試驗樣品，采用超聲脈沖回波法對其進行孔隙率無損檢測。對采集的超聲回波射頻信號進行希爾伯特變換(Hilbert Transform),并進一步濾波后得到一次底波和二次底波的包絡信號，進而計算相應的聲衰減系數；結合金相法抽檢獲得實際的孔隙率含量，標定得到超聲波衰減系數與孔隙率含量之間的經驗公式；利用該經驗公式對余下的同一批復合材料進行孔隙率檢測，并將預測結果與隨后進行的金相法檢測結果進行對比。試驗表明，這些結果具有很好的一致性，說明該方法具有一定的實用性。

復合材料；孔隙率；無損檢測；超聲波衰減法

通用飛機的綜合性能與采用的高性能復合材料、配套的制造工藝以及相關檢測方法密切相關。先進復合材料具有重量輕、比強度高、比剛度高、可設計性強、抗疲勞斷裂性能好、耐腐蝕、尺寸穩定性好以及便于大面積整體成形等優點；同時，采用整體化設計和制造技術，先進復合材料可以大幅度減少零件和緊固件數量，降低生產成本，提高飛機的可維護性。復合材料結構件用材的比例已經成為飛機先進性的重要標志。國外先進大型客機A380、787和A350復合材料用量分別達到了25%、50%和53%。我國大型運輸機和第四代戰斗機復合材料計劃用量分別為15%和30%，大型客機C919復合材料的計劃用量為25%，而國內自主研制的首款全機身復合材料某型號飛機的復合材料用量更是超過了85%。所以，通用飛機復合材料化是目前和今后的一個發展趨勢。

在復合材料越來越受到重視的同時，人們對復合材料質量的檢測與評價也越來越關注[1-4]。由于復合材料獨特的制作工藝，其材料內部總會不可避免地存在各種缺陷。通常在制造過程中形成的缺陷主要有：孔隙，疏松，分層，夾雜等。孔隙是復合材料最常見并對使用性能有重要影響的缺陷，對孔隙率(單位體積內所含孔隙的體積百分數)的鑒定是判斷復合材料質量的重要指標。研究表明[5-6]，孔隙率在4%范圍內時，每增加1%，復合材料的層間剪切性能便下降5%～15%，其他如縱/橫向拉伸強度、彎曲強度、抗壓強度等性能也受到一定的影響。由于孔隙的存在直接影響了復合材料的力學性能和可靠性，人們一直在尋找各種有效的方法來評估孔隙率含量，包括破壞性檢測法和無損檢測法。其中，超聲波檢測是一種尤為重要和有效的孔隙率無損檢測方法[6-15]，包括衰減法[6-12]、聲速法[13-14]、聲阻抗法[15]等。筆者采用水浸式超聲脈沖回波法對通用航空工業用復合材料進行檢測，對采集到的原始回波射頻信號進行希爾伯特變換(Hilbert Transform)，得到一次底波和二次底波的包絡峰值并計算相應的聲衰減系數，結合金相法測量得到的孔隙率含量，獲得聲衰減系數與孔隙率含量之間的經驗公式。通過此經驗公式，利用超聲波衰減法對余下的同一批復合材料進行孔隙率檢測，并將預測結果與隨后進行的金相法檢測結果進行對比。

1 復合材料孔隙率超聲檢測方法

1975年，英國學者STONE和CLARKE對碳纖維增強復合材料建立了超聲衰減和孔隙率之間的計算模型[7]，指出總衰減AT由3部分衰減組成，即AT=Af+At+Ab。其中，Af為前表面衰減損失；Ab為后表面衰減損失；At=αt為材料吸收損失，其中α為材料的超聲衰減系數，t為材料厚度。筆者通過試驗發現α不僅與孔隙率PV直接相關聯，而且還與超聲頻率f成正比。由于孔隙形狀在不同的孔隙率時是不同的，以孔隙率1.5%為界呈現兩個線性關系：

STONE和CLARKE的研究表明了超聲波衰減與頻率因素及孔隙含量之間的關聯性。MARTIN利用SRONE和CLARKE的數據進行了衰減系數計算并發現在頻率小于5 MHz和孔隙率小于1.5%時，數據符合得很好。1976年，MARTIN提出了在假定孔隙形狀不影響超聲波衰減情形下的衰減理論模型[8-9]。

式中：a為孔隙半徑；λ為波長；g為與縱波波速uL和橫波波速uT之比有關的參數。

由于此計算模型沒有考慮孔隙形狀對超聲波衰減的影響，在孔隙率較大時理論與實際會出現較大的偏差。1988年，HALE與ASHTON綜合考慮了孔隙形狀、大小和分布，提出了新的超聲波衰減理論模型[10]。

式中：A為與材料特性有關的常量；f為超聲波頻率；R為孔隙的最大半徑；r為孔隙的最小半徑。

由于孔隙率較大時，孔隙多呈扁平狀或條狀，即便孔隙率較小時球形或橢球形的孔隙的半徑也是很難確定的，因此該法較難應用于實際測量。

浙江大學周曉軍課題組通過分析超聲波穿過復合材料時發生衰減的主要原因，提出在選定超聲探頭頻率后，對同一批復合材料而言，由孔隙引起的超聲波衰減系數αP為關于孔隙率PV的函數[11-12]。

式中：C0，C1，C2為與材料特性有關的參數，可利用金相法抽樣試驗進行標定。

該方法具有一定的實用性，筆者主要借鑒此方法進行試驗，提出的檢測模型如圖1所示。

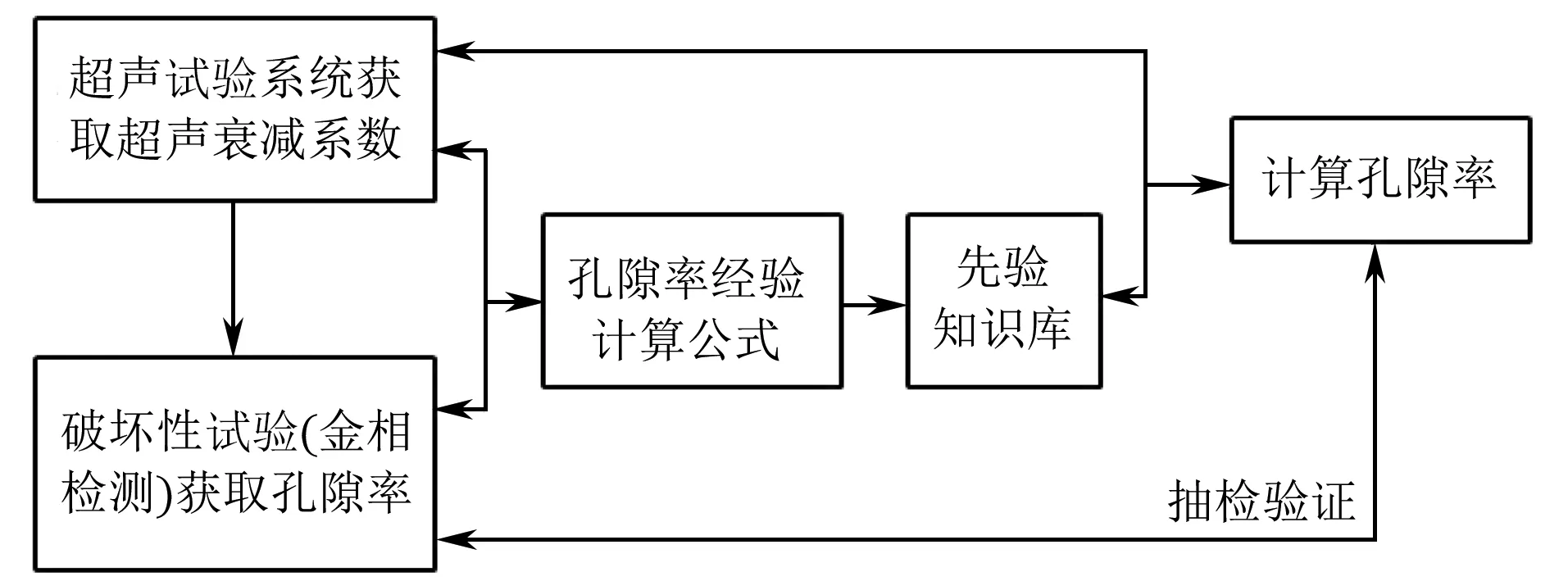
圖1 基于超聲波衰減的孔隙率檢測模型框圖

在利用超聲系統測量復合材料的聲衰減系數時，引入Hilbert 變換對采集的原始超聲回波射頻信號進行分析。Hilbert變換能克服傅里葉變換分辨率低的問題，同時又能克服小波變換后信號能量會泄露的不足[16-17]，因此，將Hilbert 變換引入對原始超聲射頻信號的分析是一個有意義的研究方向。在利用Hilbert變換得到超聲回波信號的一次底波和二次底波包絡峰值后，利用下式計算聲衰減系數。

式中：U1，U2分別為一次底波和二次底波聲壓幅值；ZW=1.5×106kg·m-2·s-1,為常溫下水的聲阻抗，試驗過程中用水做耦合劑；ZC為復合材料的聲阻抗。

式(5)考慮了二次底波對應的復合材料上表面與水的分界面的反射損失;其下表面與空氣分界，可以認為全反射，故沒有考慮其反射損失。結合式(4)和式(5)，即可計算得到孔隙率PV。

2 試驗過程及結果

試樣為國內自主研制的首款全機身復合材料某型號飛機使用的復合材料板試件，包含10塊單向碳纖維層壓板和10塊紡織玻璃纖維板，如圖2(a)，2(b)所示。為了方便測量試件的聲阻抗，試驗采用規則的方形板，使用精度為0.02 mm的游標卡尺測量其尺寸(長度、寬度、厚度)，精度為0.01 g的電子秤測量其質量，結果均為至少8次測量后再求得的平均值。由體積和質量可得到試件的密度ρC，由超聲一次底波和二次底波射頻信號及板厚計算試件的縱波聲速uC，進而根據公式ZC=ρC·uC計算其聲阻抗。

圖2 試件實物圖片

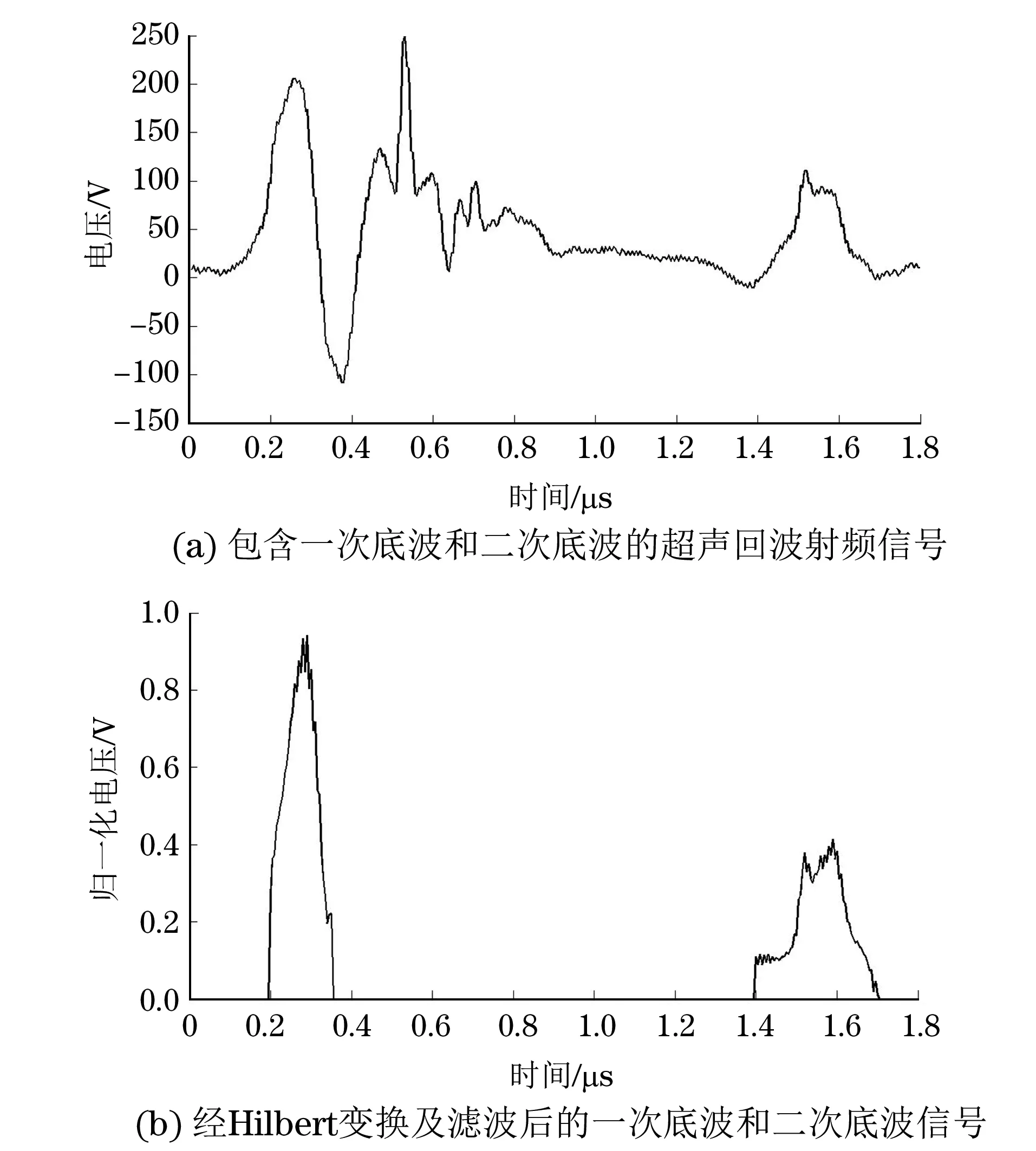
圖3 試件的超聲回波信號

檢測儀器采用CTS-1002超聲儀，配Transonic 5 MHz超聲探頭，其晶片直徑10 mm；利用UltraVision DS4034示波器進行射頻信號采集，采樣頻率200 MHz。圖3為檢測試件后得到的超聲回波信號。從圖3可看出，經Hilbert變換并濾波后的信號更好地展現了超聲波的衰減情況，能更準確更簡便地計算超聲波衰減系數。超聲檢測結束后，從兩種試件中各抽取5塊試件進行破壞性檢測(金相檢測)孔隙率含量。采用GTQ-50003高速精密切割機(主軸轉速4 202 r·min-1)及MP-2B研磨拋光機(600目粗磨，2 000目細磨)在試件不同區域分別制作規格為(長×寬)16 mm×8 mm的試樣，用金相鑲嵌儀嵌入環氧樹脂基體的試樣臺中，并利用德國萊卡公司DM 2700M金相顯微鏡進行顯微觀察。不同孔隙率試樣的金相觀察結果見圖4。萊卡應用套件中的專業軟件包能自動識別孔隙并用顏色作標記，如圖4中的綠色標識區域，可以看出，小孔隙形狀多為球形或者扁球形，而稍大的孔隙形狀趨向于長條形。由于軟件包給出的是孔隙面積與觀察截面的面積之比，即面積孔隙率，文章利用同一試件中不同剖面的面積孔隙率的平均值來表示等效體積孔隙率。

表1給出了超聲衰減系數及孔隙率金相抽檢結果(表中的編號方法：①-②-③-④；① AG300為復合材料所屬飛機型號；② 01為單向碳纖維層壓板，02為紡織玻璃纖維板；③ 表示復合材料板平均厚度，單位 mm；④ 表示厚度重復性，如2表示相同厚度第二次出現)，結合式(4)，利用最小二乘法對C0,C1,C2參數進行標定，得到如下結果：

其中C01,C11和C21為單向碳纖維層壓板的參數，C02,C12和C22為紡織玻璃纖維板的參數。將所求得的系數代入聲衰減經驗公式(4)可分別得到：

(8)

式(7)，(8)分別對應單向碳纖維層壓板和紡織玻璃纖維板的聲衰減經驗公式。

圖4 不同孔隙率試件的金相觀察結果

在獲得聲衰減經驗公式后，利用超聲檢測系統和式(5)對剩下的復合材料試件分別進行檢測和計算，將得到的聲衰減系數分別代入聲衰減經驗公式(7)，(8)，并利用式(6)計算得到相應的孔隙率。為了檢驗孔隙率計算結果的準確性，隨后對這些復合材料試件進行金相法檢測，并將金相檢測結果與上述超聲波衰減法計算得到的孔隙率結果進行對比，詳細數據及對比結果如表2所示。從對比結果可看出，利用超聲波衰減法計算得到的孔隙率含量與利用金相法檢測得到的孔隙率含量具有很好的一致性，單向碳纖維層壓板的檢測結果誤差很小，紡織玻璃纖維板的誤差相對大一些，但最大誤差也僅為0.388%，在可接受的范圍內。

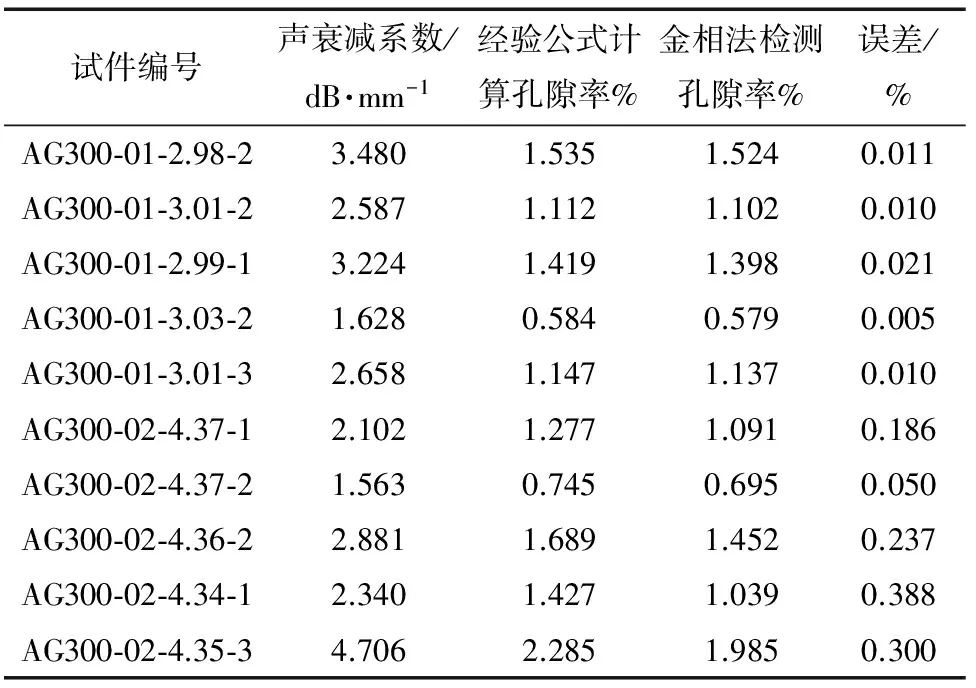
表2 孔隙率的經驗計算及驗證

3 結論

以國內自主研制的首款全機身復合材料某型號飛機使用的復合材料板試件為試驗樣品，采用水浸式超聲脈沖回波法對其進行孔隙率無損檢測，對采集到的原始回波射頻信號進行希爾伯特變換，得到一次底波和二次底波的包絡峰值，并計算相應的聲衰減系數，結合金相法檢測得到的孔隙率含量，獲得聲衰減系數與孔隙率含量之間的經驗公式。利用此聲衰減經驗公式對余下的同一批復合材料進行孔隙率檢測，并將預測結果與隨后進行的金相法檢測結果進行對比。試驗結果表明，這些結果具有很好的一致性，說明該方法具有一定的實用性。

該種方法假定孔隙率經驗公式中的待定系數對同一批復合材料試件保持不變。在實際應用中，由于復合材料加工工藝的復雜性和特殊性，即便是同一批復合材料，也不能完全保證其聲衰減特性的一致性，利用抽樣法獲取的聲衰減經驗公式可能會存在誤差，因此如何獲取更為準確和實用的聲衰減經驗公式值得進一步研究。另外，在超聲波檢測過程中，由于復合材料試件一般很薄，為了減小近場的影響，應選擇小直徑低頻超聲探頭，但探頭頻率低則軸向分辨力也低，因此實際應用中應平衡考慮。

[1] 史俊偉，劉松平，程文禮. 復合材料蜂窩夾層結構制件的超聲可視化無損檢測[J]. 無損檢測，2015，37(3):39-43.

[2] 張繼敏，周暉，劉奎. 復合材料層壓結構超聲相控陣檢測的缺陷定量表征[J]. 無損檢測，2016，38(1):20-25.

[3] 紀瑞東，張旭剛，王玨. 飛機復合材料構件的原位紅外熱成像檢測[J]. 無損檢測，2016，38(1):13-16.

[4] 董方旭，王從科，凡麗梅.X射線檢測技術在復合材料檢測中的應用與發展[J].無損檢測，2016，38(2):67-72.

[5] GHIORSE S R. Effect of void content on the mechanical properties carbon / epoxy laminates[J]. SAMPE, 1993(9):54-59.

[6] JEONG H. Effects of voids on the mechanical strength and ultrasonic attenuation of laminated composites[J]. Journal of Composite Materials, 1997, 31(3):276-292.

[7] STONE D E, CLARKE B. Ultrasonic attenuation as a measure of void content in carbon fiber reinforced plastics[J]. Non-destructive Testing, 1975, 8(3): 137-145.

[8] MARTIN B G. Ultrasonic attenuation due to voids in fiber reinforced plastic[J]. Non-destructive Testing International, 1976, 9(5):242-246.

[9] MARTIN B G. Ultrasonic wave propagation in fiber reinforced solids containing voids[J]. Journal of Applied Physics, 1977, 48(8):3368-3369.

[10] HALE J M, ASHTON J N. Ultrasonic attenuation in voided fiber reinforced plastic[J]. Non- destructive Testing International, 1988, 21(5):321-326.

[11] 周曉軍，莫錦秋，游紅武. 碳纖維復合材料分布孔隙率的超聲衰減檢測方法[J]. 復合材料學報，1997，14(3):107-113.

[12] 宋立軍. 復合材料孔隙率檢測方法及其實現技術的研究[D]. 杭州：浙江大學，2005.

[13] HSU D K, JEONG H. Ultrasonic velocity change and dispersion due to porosity in composite laminates[C]∥ Review of progress in quantitative nondestructive evaluation.Iowa:Springer US,1989: 1567-1573.

[14] JEONG H, HSU D K. Experimental analysis of porosity induced ultrasonic attenuation and velocity change in carbon composites[J]. Ultrasonic, 1995, 33(3):195-203.

[15] 林莉，羅明，郭廣平，等. 碳纖維復合材料孔隙率超聲聲阻抗法檢測[J].復合材料學報， 2009， 26(3): 105-110.

[16] 馬云闊，戴光，李偉. 基于小波包特征熵的碳纖維復合材料損傷聲發射信號特征提取方法[J]. 無損檢測，2017，39(5):76-80.

[17] IVAN W, SELESNICK. Hilbert transform pairs of wavelet bases[J]. Signal Processing Letters, 2001, 8(6):170-173.

EstimationofAeronauticalCompositePorositybyUsingUltrasonicWaveAttenuation

SHENYang1,YOUYong1,GUOZhiwen2,ZHANGGuocai1,XINGXiuwen1,XIEXiaorong1

(1.SchoolofAppliedScienceandCivilEngineering,BeijingInstituteofTechnology,Zhuhai,Zhuhai519088,China;2.AVIGENERALHuananAircraftIndustryCo.,Ltd.,Zhuhai519088,China)

Ultrasonic techniques for measuring void content were discussed and the composites used for the whole fuselage composite aircraft developed independently in China were chosen as experimental specimens, including 10 unidirectional carbon fiber laminates and 10 textile glass fiber sheets. The ultrasonic RF signals were processed using Hilbert transform and spectral-filter and then used to calculate the acoustic attenuation. The relationship between attenuation coefficient and porosity was calibrated by sampling experiment based on metalloscopy. The calibrated relational expression was then used to estimate the porosity of the rest specimens. The experimental data showed that the ultrasound testing results were in agreement with the metallographic detection.

composite; porosity; nondestructive testing; ultrasound wave attenuation

TG115.28

A

1000-6656(2017)10-0059-05

2017-07-06

廣東省普通高校特色創新資助項目(自然科學類)(ZX-2017-001)；珠海市高端制造業協同創新中心無損檢測分中心資助項目(ZX-2015-063)；北京理工大學珠海學院科研發展基金資助項目(XK-2015-22)

沈 洋(1980-),男，講師，主要從事超聲無損檢測技術教學、研究及工程應用工作

游 泳(1976-)，男，副教授，主要從事超聲無損檢測技術教學、研究及工程應用工作，12696767@qq.com

10.11973/wsjc201710013