雙殼油船破艙原油泄漏縮尺模型相似準則

盧金樹, 吳豪霄, 楊振波

(浙江海洋大學 海運與港航建筑工程學院， 浙江 舟山 316022)

2017-04-15

國家自然科學基金委員會面上項目(51079129)；浙江省自然基金(LY18E090008)

盧金樹(1974—),男,浙江象山人,教授,從事船舶安全與污染控制研究。E-mail:ljs_ljs@zjou.edu.cn

1000-4653(2017)03-0103-06

雙殼油船破艙原油泄漏縮尺模型相似準則

盧金樹, 吳豪霄, 楊振波

(浙江海洋大學 海運與港航建筑工程學院， 浙江 舟山 316022)

為使雙殼油船原油泄漏縮尺模型試驗能真實地反映事故原型，需確定各相似準則的重要程度。針對油艙原油泄漏過程，基于相似理論，采用量綱分析的方法推導較完整的相似準則數群，根據不同相似準則的組合建立3種縮尺模型。進行原型和不同相似準則縮尺模型的數值試驗，并根據相似關系將縮尺模型試驗的泄漏持續時間、泄漏總量等宏觀泄漏特征參數反推回原型，與原型數值試驗結果相對比。采用黏性流體動力學理論分析各種作用力對泄漏過程的影響。結果表明:弗汝德相似準則和雷諾相似準則是原油泄漏縮尺模型試驗必須依據的準則，韋伯相似準則可不予考慮。在試驗油品和原油密度相同的情況下，縮尺模型試驗結果與原型最為接近。針對不同泄漏階段，應采用不同的縮尺模型進行試驗。

船舶工程;縮尺模型；相似準則；原油泄漏；雙殼油船；黏性流體動力學

在原油泄漏研究中，原油泄漏規律的精準預測是研究者關注的兩大工程問題之一。[1-2]針對該問題，通常采用理論分析、數值模擬和模型試驗等方法進行研究。由于油品泄漏涉及到的流動行為復雜多樣，采用理論分析方法時需對泄漏預測模型進行大量簡化，導致模型精度不高。大尺度模型試驗能得到較為真實的原油泄漏規律，但大尺度模型艙的制作成本較高，且原油泄漏會造成嚴重的環境污染。[3]因此，通常采用小尺度縮尺模型試驗的方法研究原油泄漏規律。[4-7]縮尺模型試驗的精度主要受以下3個因素影響：

1) 確定原油泄漏過程的主導力，選取合理的相似準則。

2) 選取表征泄漏特征的特征長度。

3) 選取適當大小的縮尺比。

關鍵作用力的相似準則缺失、表征泄漏特征的特征長度選擇錯誤及縮尺比過小都有可能引發縮尺效應。根據建立縮尺模型所依據的相似準則分類，采用的縮尺模型主要有弗汝德相似準則模型(以下簡稱Fr模型)和弗汝德-雷諾相似準則模型(以下簡稱Fr-Re模型)2種。

Fr模型是早期的原油泄漏模型試驗中采用的縮尺模型，主要用來探究雙殼油船和中層甲板油船的阻漏效果。[8-9]由于Fr模型只考慮重力的相似，忽略黏性力的相似，不可避免地會產生縮尺效應。[8]此外，由于原油泄漏過程中存在流動變態行為，在舷側破艙原油泄漏的密度差流階段[10-11]，油品泄漏的動力并非重力。在這種情形下，Fr模型就不能真實地反映原型的泄漏過程。

考慮到黏性力未相似會引發縮尺效應，文獻[12]針對單殼油船原油泄漏情形，提出同時考慮重力和黏性力相似的Fr-Re模型。該縮尺模型是在滿足Fr相似的前提下，選取特定黏度的油品進行試驗，使模型的雷諾數與原型相等。當縮尺比較大時，難以找到黏度符合要求的油品[13]，使得該模型具有一定的局限性，而且忽略了表面張力和浮力，采用該模型進行試驗時可能會引發縮尺效應。

基于上述情況,首先對原油泄漏過程進行受力分析，確定影響原油泄漏的相關作用力。基于相似理論，對油艙原油泄漏過程進行量綱分析，推導出較為完整的相似準則數群，并據此建立3種不同的縮尺模型。在相同縮尺比下，通過對比分析3種縮尺模型的泄漏持續時間、泄漏速度和泄漏入海量等宏觀泄漏特征參數，確定影響原油泄漏的主要作用力，最終得到建立縮尺模型必須依據的相似準則。

1 原油泄漏受力分析

雙殼油船水下破艙原油泄漏是多種流動行為復合的過程。在不同損傷情形下，原油泄漏的主導力不同，且作用強度會隨著泄漏過程的進行而發生改變。這里以靜水環境中的雙殼油船底部破艙泄漏情形為例，分析原油泄漏過程中的相關作用力。

圖1為雙殼油船原油泄漏示意，由于雙層底空間的存在，從油艙中泄漏出的原油不會直接泄漏到外界，而是先泄漏到雙層底中，隨后穿透雙層底過程中的水層泄漏到外界。[7]通常認為原油從油艙泄漏到雙層底中的流動屬于重力主導下的孔口出流，其流動行為還受黏性力和油-氣表面張力的影響。[8]然而，在原油穿透雙層底中的水層泄漏到外界的過程中，其還會受到浮力的作用。在這些作用力中，重力是驅動原油泄漏的力(動力)，而黏性力、表面張力和浮力均是阻礙原油泄漏的力(阻力)。當某個作用力未按相同縮尺比縮小時，就會導致動力和阻力的相對大小發生變化，從而引發縮尺效應。

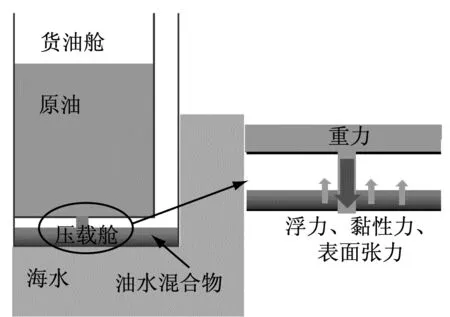
圖1 雙殼油船原油泄漏示意

2 縮尺模型的建立

目前已有研究采用的縮尺模型均未考慮表面張力和浮力。表面張力和浮力分別在油艙及雙層底中起作用。這里以油艙為研究對象，針對原油從油艙泄漏到雙層底的過程，采用量綱分析的方法推導出考慮表面張力的較為完整的相似準則數群，并據此建立縮尺模型。

2.1油艙油品泄漏量綱分析

內殼破孔處的原油泄漏平均速度v是衡量原油泄漏特征的重要指標。相關參數有油艙油位H，破孔孔徑d，重力加速度g，油品密度ρ，油品動力黏度系數μ和表面張力系數σ。描述油艙油品泄漏速度的一般函數式為

f(v,H,ρ,g,d,μ,σ)=0

(1)

式(1)中:物理量的個數為n=7，采用[M],[L],[T]等3個基本量綱，m=3。根據π定理，這n個物理量的關系式可轉換成n-m=4個無量綱量的函數關系式,即

f(π1,π2,π3,π4)=0

(2)

選擇H,ρ,g等3個物理量作為基本物理量，其余4個參數可表示為

(3)

根據量綱一致性原理得到4個無量綱數,即

(4)

式(3)和式(4)中:π1為弗汝德數;π2為幾何無量綱數;π3和π4分別可轉換為雷諾數及韋伯數。弗汝德數、雷諾數和韋伯數分別是重力、黏性力及表面張力的相似準則。根據滿足的相似準則個數的不同，可建立Fr模型、Fr-Re模型和弗汝德-雷諾-韋伯模型(以下簡稱Fr-Re-We模型)等3種縮尺模型。

2.2原油泄漏模型參數相似關系的導出

用m和p分別表示模型參數及原型參數。取幾何比尺為λ=lp/lm，根據推導的相似準則導出模擬油艙原油泄漏過程的縮尺模型各參數與原型的相似關系。

1) 速度相似關系為vp=vmλ1/2。

2) 破孔孔徑相似關系為dp=dmλ。

3) 油品動力黏度相似關系為μp=μmλρλ3/2。

4) 油品表面張力系數相似關系為σp=σmλρλ2。

5) 當模型的油品密度與原型相等時，動力黏度與表面張力系數相似關系分別簡化為μp=μmλ3/2和σp=σmλ2。

根據幾何相似關系和速度相似關系，可導出時間相似關系tp=tmλ1/2和油品體積相似關系Vp=Vmλ3。基于不同相似準則建立的不同縮尺模型主要比尺見表1。

表1 不同縮尺模型主要比尺

3 不同相似準則縮尺模型研究

選取的相似準則越合理，根據相似關系將縮尺模型試驗結果反推回原型尺度得到的模型-原型結果與實際原型結果越接近。通過對比不同縮尺模型的油品泄漏特征參數與原型的偏差，即可判斷出各相似準則的重要程度。參考相關研究[7]，以某超大型油船的L型油艙邊艙為模型艙原型，以Lone Rock原油為油品原型，根據表1設計縮尺模型試驗。采用數值試驗的方法模擬原型和各縮尺模型的油品泄漏過程。通過對比模型自由泄漏階段持續的時間及油品泄漏入海量與原型的差異，探究油品泄漏過程中黏性力、表面張力和浮力的相對重要程度，進而確定建立縮尺模型時應采用的相似準則。

3.1縮尺模型試驗設計依據

在縮尺模型試驗中，模型縮尺比確定之后，可通過改變特征流速v和選取具有特定黏度μ的液體作為流體介質2種方法控制模型雷諾數Re=ρvd/μ。然而,在原油泄漏模型試驗中，無法人為改變流速，只能通過選取具有特定黏度的油品控制模型的雷諾數。[13-14]同樣，模型的韋伯數也通過改變油品的表面張力系數來控制。

3.2縮尺模型油品物性及模型幾何參數的確定

小尺度縮尺模型試驗的縮尺比通常為1:50～1:30，因此選取1:40作為縮尺模型的縮尺比。根據表1中的油品物性相似關系和模型幾何特征相似關系，確定縮尺模型試驗對照組的油品物性和模型幾何參數(見表2)。此外，為探究浮力對油品泄漏的影響，設置試驗油品密度和Fr-Re-We模型不同的對照組Fr-Re-We(D)。

為保證縮尺模型與原型的幾何相似性，在原型和縮尺模型的幾何模型中均忽略船殼厚度。簡化的模型艙示意見圖2。

a)正視圖b)俯視圖

圖2 簡化的模型艙示意

3.3研究方法及驗證

該研究采用文獻[15]給出的數值方法，經物模試驗驗證，該方法能較為準確地模擬油品泄漏過程。

3.4不同相似準則縮尺模型的試驗結果

相似準則數反映各種作用力和慣性力的相對大小。根據Fr模型、Fr-Re模型、Fr-Re-We模型和Fr-Re-We(D)模型試驗結果，分析黏性力、表面張力和浮力對原油泄漏的影響，從而確定縮尺模型試驗應采用的相似準則。

3.4.1不同相似準則下的泄漏持續時間

理論上，當所有作用力都按相同比例縮小時，根據相似關系將縮尺模型結果反推回原型得到的結果應與原型相同。當某個相似準則未考慮(即某個作用力未按縮尺比縮小)時，縮尺模型轉化到原型的結果會與原型產生偏差，該偏差就是該作用力未縮尺產生的縮尺效應。不同縮尺模型油品自由泄漏階段持續時間見圖3。從圖3中可看出,Fr-Re模型和Fr-Re-We模型的泄漏持續時間與原型最為接近，Fr-Re-We(D)模型次之，Fr模型偏差最大。這說明黏度偏大、密度偏小會導致原油自由泄漏階段持續時間偏短，黏性力和浮力是引發縮尺效應的主要原因。

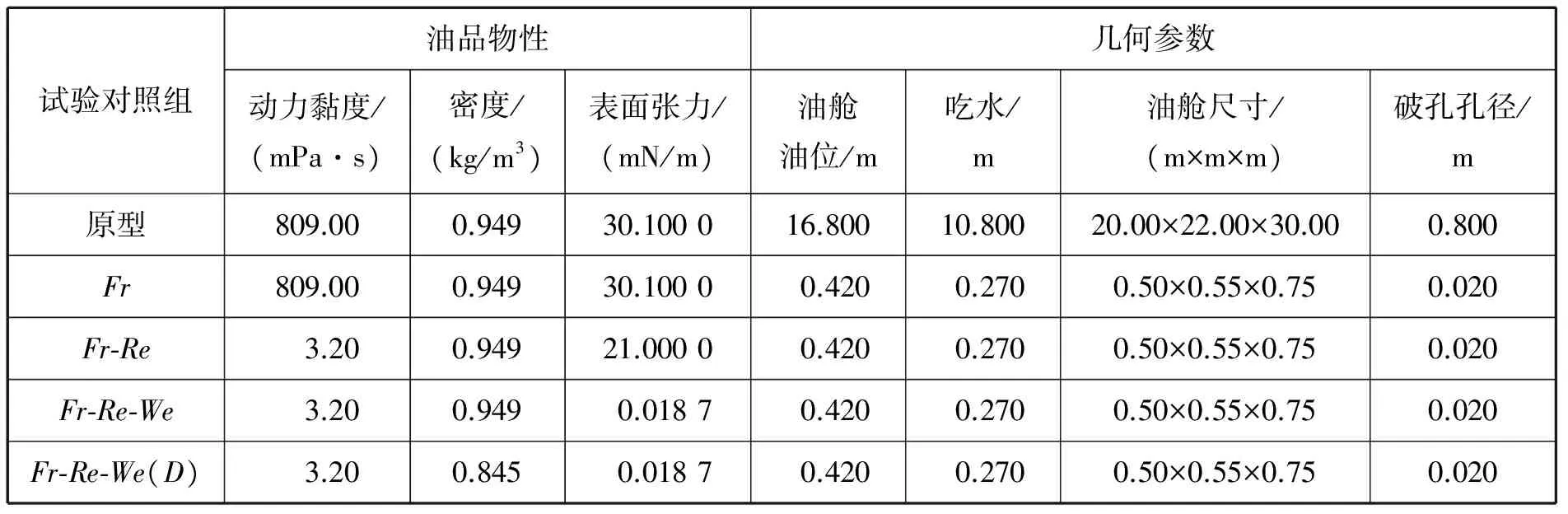
表2 原油泄漏縮尺模型試驗對照組

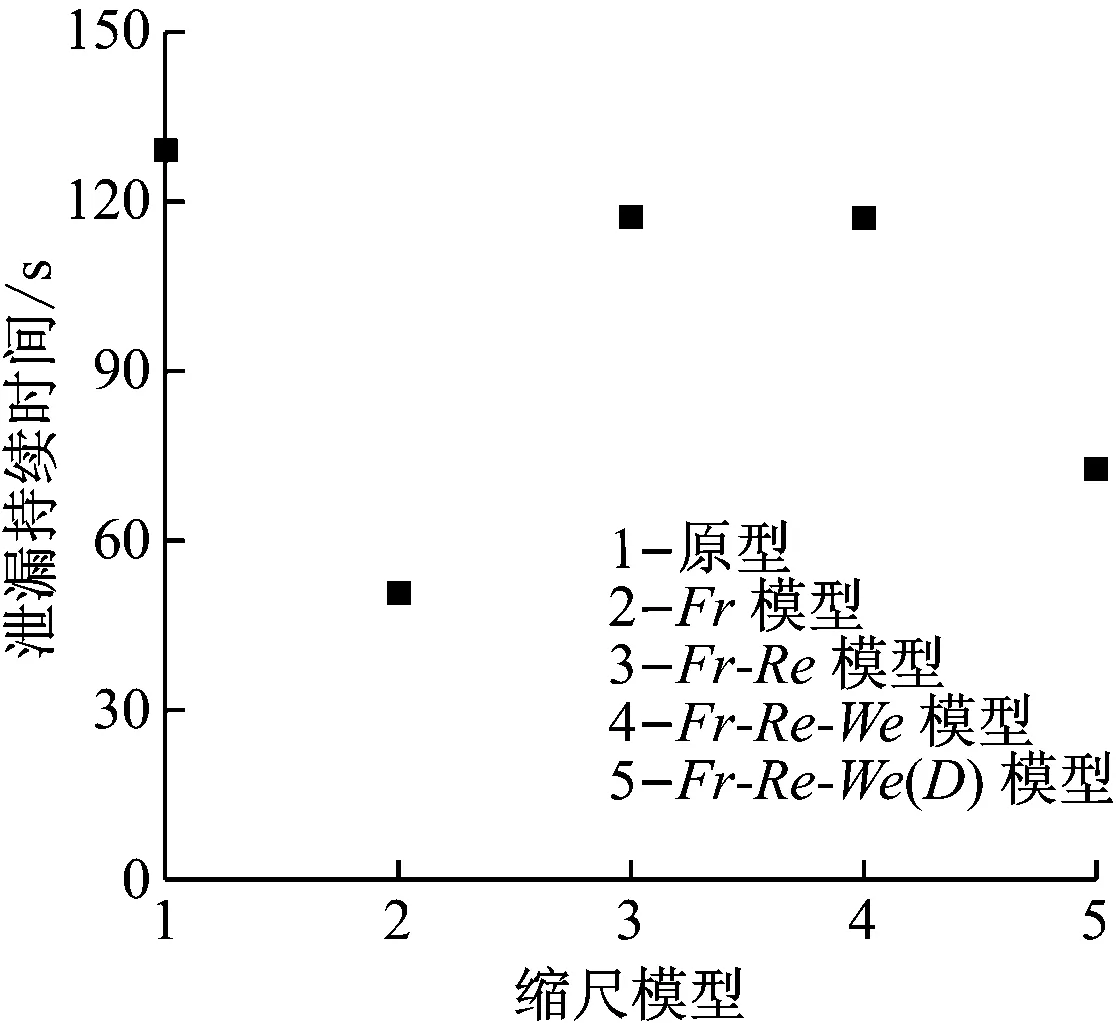
圖3 不同縮尺模型油品自由泄漏階段持續時間

Fr-Re-We模型是在Fr-Re模型的基礎上考慮韋伯相似準則得到的縮尺模型。通過對比Fr-Re模型和Fr-Re-We模型可探究表面張力對原油泄漏的影響。圖3中，2個縮尺模型的油品泄漏速度和油品從外殼破孔泄漏入海的平均速度均基本相同，說明在油品泄漏過程中表面張力的作用可忽略不計。

從圖3～圖7中可看出，Fr-Re模型和Fr-Re-We模型已能較為真實地反映原型，但仍存在偏差，這可能是未采用相應的相似準則對油水界面張力進行縮尺導致的。

Fr-Re模型是在Fr模型的基礎上考慮雷諾相似準則得到的縮尺模型。通過對比Fr模型和Fr-Re模型可探究黏性力對原油泄漏的影響。圖4為不同縮尺模型油艙油品泄漏平均速度。從圖4中可看出，Fr模型中油品從油艙破孔泄漏進入雙層底的平均速度略小于Fr-Re模型。這是因為Fr模型僅保證重力的相似，而黏性力未按相同比例縮小。當采用原油作為試驗油品時，由于其黏度遠大于黏性力相似應采用的油品黏度[10]，導致油品在油艙中流動的阻力偏大，油艙油品泄漏平均速度偏小。

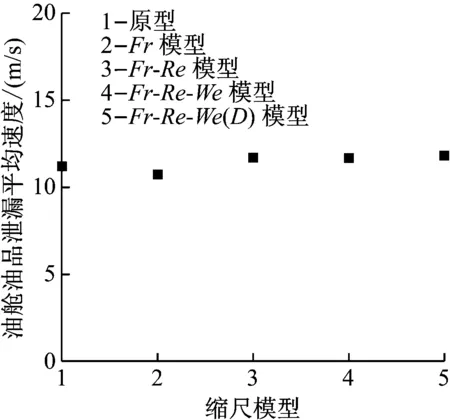
圖4 不同縮尺模型油艙油品泄漏平均速度

在Fr模型中，油品進入雙層底之后，由于油艙中的油品泄漏速度偏小，油射流所具備的動能不足以克服自身的浮力和水層的阻力，導致油品泄漏入海率遠低于原型。此外，由于油射流不能占據外殼破孔，使得外界海水大量進入雙層底。在這2方面的綜合作用下，Fr模型的雙層底液位上升速度遠大于原型和其他縮尺模型，最終導致該模型自由泄漏階段持續時間遠小于原型。因此，黏性力是原油泄漏過程中的重要作用力，當黏性力未按相同比例縮小時，會導致縮尺模型自由泄漏階段持續時間存在縮尺效應。這也說明在進行縮尺模型試驗時，不能選取原油作為試驗油品，而應根據雷諾相似準則選取特定黏度的油品。

Fr-Re-We(D)模型是在Fr-Re-We模型的基礎上改變試驗油品密度得到的縮尺模型。通過對比Fr-Re-We(D)模型和Fr-Re-We模型可探究浮力對原油泄漏的影響。圖5為不同縮尺模型油品泄漏入海平均速度，2種模型的油艙油品泄漏速度基本相同，Fr-Re-We(D)模型的油品泄漏入海平均速度小于Fr-Re-We模型，與原型的偏差更大。

上述試驗證明油品在穿透雙層底中的油水混合物時會受到浮力的影響。當油品密度小于原油時，油品與海水的密度差變大，油品在油水混合物中流

圖5 不同縮尺模型油品入海泄漏平均速度

動時受到的凈浮力變大，油品泄漏入海的速度變小。泄漏入海速度變小意味著更多油品被保留在雙層底中，雙層底液位上升速度加快，自由泄漏階段持續時間變短(如圖3所示)。因此，浮力是油品泄漏過程中的另一個重要作用力，當其未按相同比例縮小時，會導致縮尺模型自由泄漏階段持續時間存在縮尺效應。

由于油品密度發生改變，Fr-Re-We(D)模型的雷諾數并不與Fr-Re-We模型相同，但數值非常接近。然而,油品泄漏入海的速度與Fr-Re-We模型存在很大偏差，這說明僅保證雷諾數相同不能準確模擬原油在雙層底中的流動行為。油品的密度和黏度是2個獨立的影響因子，通過控制油品的運動黏度來控制雷諾數相同是不可行的。

3.4.2不同相似準則下的油品泄漏入海量

油品泄漏入海量是另一個重要的油品泄漏特征參數。不同縮尺模型自由泄漏階段油品泄漏入海量見圖6。從圖6中可看出，Fr-Re模型和Fr-Re-We模型的泄漏入海量與原型最為接近，Fr-Re-We(D)模型和Fr模型的偏差均較大。這說明黏性力和浮力也會導致油品泄漏入海量存在縮尺效應。

圖6 不同縮尺模型自由泄漏階段油品泄漏入海量

油艙油品泄漏量取決于自由泄漏階段持續時間和油品泄漏入海的平均速度。由于Fr模型未對黏性力進行縮尺，采用原油作為試驗油品會導致油品泄漏平均速度偏小，自由泄漏階段持續時間偏短。這2個參數偏小均會導致油艙油品泄漏量偏少(見圖7)。

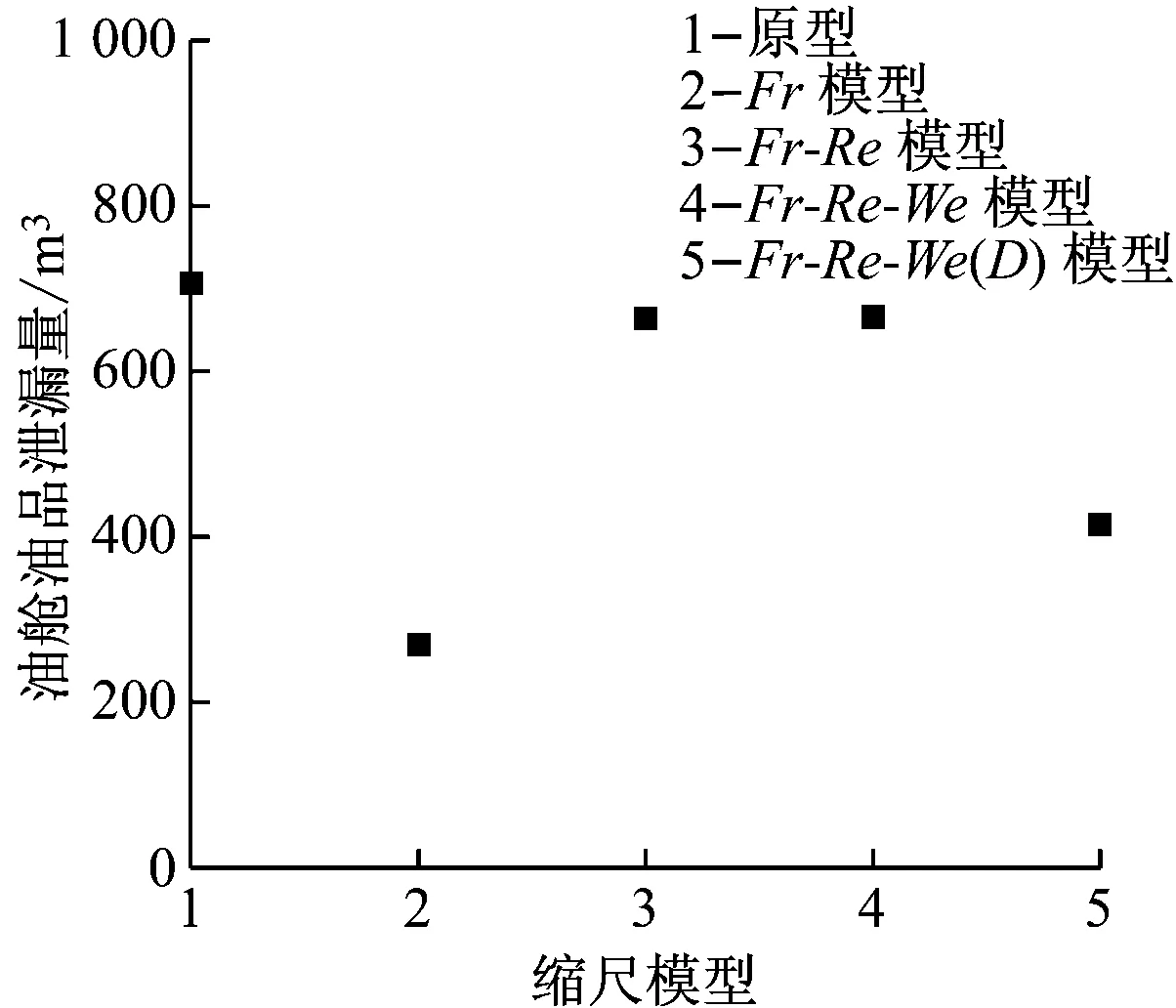
圖7 不同縮尺模型油艙油品泄漏量

由于黏性力過大，使得油射流不能穿透雙層底中的水層泄漏到外界，直接改變雙層底中油水相互作用形式，導致模型油品泄漏入海量與原型存在巨大偏差(如圖6所示)。這進一步證明要采用縮尺模型模擬原油泄漏過程,必須根據雷諾相似準則選取低黏度的油品作為試驗油品。

在自由泄漏階段，油艙中的油品與雙層底中的油水混合物并未發生直接作用，浮力僅對雙層底中的油品產生作用，因此Fr-Re-We(D)模型的油艙油品泄漏速度與Fr-Re-We模型基本相同。由于Fr-Re-We(D)模型采用的油品與海水的密度差更大，油品在雙層底中流動時所受凈浮力更大，油射流速度衰減更嚴重。因此,Fr-Re-We(D)模型的油品泄漏率偏小，雙層底中油品積累的速度偏大，自由泄漏階段持續時間偏短。雖然Fr-Re-We(D)模型油艙油品泄漏速度與Fr-Re-We模型相同，但Fr-Re-We(D)模型自由泄漏階段持續時間更短，導致油艙泄漏量偏少。在油艙泄漏量和油品泄漏入海率均減小的情況下，Fr-Re-We(D)模型自由泄漏階段的油品泄漏入海量偏少(如圖6所示)。

綜上所述，當模型中的油品所受的黏性力和凈浮力偏大時，會導致自由泄漏階段持續時間縮短，該階段的油品泄漏入海量減少。然而,在進行縮尺物模試驗時，較難使浮力和黏性力的大小同時滿足相似準則的要求，這勢必會導致自由泄漏階段結束時的油品泄漏特征參數存在縮尺效應。若縮尺模型進入原油受阻泄漏階段時的油艙油位和油艙油品泄漏速度(轉化到原型尺度)與原型存在偏差，則受阻泄漏階段的縮尺效應可能會被進一步放大。

4 結束語

針對原油自由泄漏階段的油艙原油泄漏過程，基于相似理論，采用量綱分析的方法推導出完整的相似準則數群，并根據不同相似準則建立3種縮尺模型。通過數值試驗的方法模擬相同縮尺比下不同縮尺模型的油品泄漏過程，根據相似關系將縮尺模型數值試驗結果轉換為原型尺度，將其與原型數值試驗結果相對比，驗證通過選取低黏度油品控制模型雷諾數的科學性。研究結果表明：

1) 黏性力和浮力是影響原油泄漏過程的重要作用力，這2個作用力未按相同縮尺比縮小是引發縮尺效應的主要原因。油-氣表面張力在原油泄漏過程中可忽略不計。

2) 在進行縮尺物模試驗時，應根據傅汝德相似準則建立縮尺模型，根據雷諾相似準則選取適當黏度的油品或盡量選取黏度小的油品，油品密度應與原油相等或接近，以降低縮尺效應的影響。

[1] HYSING T, TORSET O. Reduction of Oil Outflows at Collisions and Groundings Through Improved Vessel Design Arrangement[J]. Marine Pollution Bulletin, 1994, 29(6): 368-374.

[2] WIEL G V D, DORP J R V. An Oil Outflow Model for Tanker Collisions and Groundings[J]. Annals of Operations Research, 2011, 187(1): 279-304.

[3] 蘭國新, 李穎, 劉丙新, 等. 基于多源遙感的海上溢油檢測研究[J]. 中國航海, 2013, 36(1): 115-120.

[4] TAVAKOLI M T, AMDAHL J, LEIRA B J. Investigation of Interaction Between Oil Spills and Hydrostatic Changes[C]. ASME International Conference on Ocean, Offshore and Arctic Engineering, 2009: 803-811.

[5] TAVAKOLI M T, AMDAHL J, LEIRA B J. Analytical and Numerical Modelling of Oil Spill from a Side Tank with Collision Damage[J]. Ships and Offshore Structures, 2012, 7(1): 73-86.

[6] 趙衛斌, 盧金樹, 朱哲野, 等. 油船水下破艙原油泄漏模型試驗設計[J]. 浙江海洋學院學報(自然科學版), 2013, 32(3): 255-259.

[7] LU J S, LIU F C, ZHU Z Y. Effects of Initial Water Layer Thickness on Oil Leakage from Damaged DHTs[C]. The Twenty-Fourth International Ocean and Polar Engineering Conference, 2014: 618-625.

[8] KARAFIATH G. Accidental Oil Spill Due to Grounding: Summary of Model Test Results. Summary Report, Jan-Jun 92[R]. Bethesda, MD Naval Surface Warfare Center, 1992: 1-61.

[9] YAMAGUCHI K, YAMANOUCHI H. Oil Spills from the Double Hull Model Tanks[J]. Report of Ship Research Institute, 1992, 29: 1-38.

[10] 盧金樹. 油船水下破艙油品泄漏動力學機理及特性研究[D]. 大連:大連海事大學, 2015:49-51.

[11] 盧金樹, 劉楓琛, 吳文鋒, 等. 破孔高度對油船水下破艙油品泄漏的影響[J]. 大連海事大學學報, 2015,41(2): 46-50.

[12] SIMECEK-BEATTY D, LEHR W J, LANKFORD J. Leaking Tank Experiments for Heavy Oils[J]. Beatty, 2012(1): 127-131.

[13] TAVAKOLI M T, AMDAHL J, LEIRA B J. Experimental Investigation of Oil Leakage from Damaged Ships Due to Collision and Grounding[J]. Ocean Engineering, 2011, 38(17): 1894-1907.

[14] SIMECEK-BEATTY D, LEHR W J, LANKFORD J F. Leaking Tank Experiments With Orimulsion and Canola Oil[J]. National Oceanic and Atmospheric Administration, 2003(12): 30.

[15] 盧金樹, 劉楓琛, 朱哲野. 雙殼油船底部破艙水下原油泄漏過程三維數值模擬[J]. 江蘇科技大學學報 (自然科學版), 2014, 28(5): 423-428.

SimilarityCriteriaofPhysicalModelingforCrudeOilLeakagefromDoubleHullOilTanker

LUJinshu，WUHaoxiao，YANGZhenbo

(School of Maritime and Civil Engineering， Zhejiang Ocean University， Zhoushan 316022， China)

Laboratory investigation of oil leakage from double hull oil tank requires the selection of an adequate similitude. In order to ensure the rationality of the scale model tests, the dimension analysis method is used to deduce the similarity criteria that are required in the scale model test. Based on these similarity criteria, three different kinds of scale models are presented. Numerical simulation for the prototype and its 1/40 scale models based on different similitude criteria are carried out. According to the similarity criteria, the result from the scale model is extrapolated to the prototype flow conditions and compared with those directly calculated from the prototype. Based on the viscous fluid dynamics, the effects of viscous force, surface tensional force and buoyant force on the crude oil leakage process are analyzed. The results indicate that the Froude and Reynolds similarity criteria are the dominant similarity criteria and Weber criteria is negligible. When the density of oil used in the model is equal to that of crude, the scale effect is minimized. In different oil leakage stage, different scale model is required to simulate the oil leakage process.

ship engineering; scale model； similarity criteria； oil leakage； double hull oil tanker； viscous fluid dynamics

X55;U674.133.1

A