改進的迭代卡爾曼濾波及其在全球導航星系統/慣導緊組合中的應用

化雪薈,陳大力

(佛山職業技術學院,廣東 佛山 528000)

改進的迭代卡爾曼濾波及其在全球導航星系統/慣導緊組合中的應用

化雪薈*,陳大力

(佛山職業技術學院,廣東 佛山 528000)

為改善GNSS/INS(Global Navigation Satellite System/Inertial Navigation System)緊組合中非線性濾波器的穩定性和精度,基于Backtracking線搜索(BLS)方法提出一種新型的迭代容積卡爾曼濾波方法(BLS-ICKF)。首先建立Sigma點濾波方法的迭代框架,采用阻尼Newton迭代改善狀態初始誤差較大時的濾波更新精度,同時,為提高組合系統狀態預測過程的魯棒性定義了一種簡化的迭代更新結構。實驗和仿真結果表明,BLS-ICKF犧牲較小的時間復雜度較CKF的航向角誤差減少約59%。

組合導航;迭代濾波框架;容積卡爾曼濾波;Backtracking線搜索

以GPS為代表的GNSS受短時信號衰減和干擾影響較大,而慣性器件的噪聲和漂移導致慣性導航系統(INS)誤差隨運行時間積累,因此兩者誤差具有互補特性。近年來,融合兩者信息的組合導航系統獲得了廣泛的應用,由于INS狀態誤差方程和GNSS偽距、偽距率觀測方程具有非線性特征,兩者的信息融合屬于典型非線性濾波問題。擴展卡爾曼濾波器(EKF)是一種廣泛采用的非線性濾波方法,其采用線性截斷逼近濾波過程中的非線性,當系統中存在較強的非線性時易發散,且EKF實現過程需要計算雅克比矩陣。以無跡變換(UT)為代表的采樣逼近方法獲得了廣泛的關注,Julier[1]將UT引入卡爾曼濾波(KF)過程提出了 UKF,分析結果表明其較EKF具有更高的非線性逼近精度,且無需計算雅克比矩陣。然而,在處理高階系統問題時,UKF需要特殊的采樣策略保證濾波穩定性,Arasaratnam基于三階Spherical-Radial準則提出了具有較好穩定性的CKF[2],本文將采用確定性采樣的濾波方法統稱為 Sigma點濾波。

文獻[3]對比分析了EKF和Sigma點濾波在組合導航中的性能,結果表明初始姿態誤差較大時后者具有較快的收斂速度。Wendel等人[4-5]基于GNSS/INS緊組合模型分析了兩者的性能,結果表明Sigma點濾波較EKF并無優勢。然而,上述分析均沒有考慮濾波過程中狀態的可觀測性問題,Zhao[6]基于車載導航系統的狀態可觀測分析對CKF和EKF的性能進行了驗證,結果表明當系統非線性較強或狀態可觀測性較弱時,CKF優于EKF。鑒于Zhao和 Wendel的結論不一致,即Sigma點濾波方法是否能改進緊組合導航性能尚無一致結論,因此有必要對適用于GNSS/INS緊組合的非線性濾波方法進一步驗證。無論是Sigma點濾波還是EKF,其濾波過程都包括狀態先驗和量測似然分布的逼近,且均基于KF框架完成狀態估計。Morelande等人[7]的研究表明只有當觀測量的信噪比較低時,Sigma點濾波逼近狀態后驗概率密度函數(PDF)才優于KF。目前大多數非線性濾波的研究集中在新型的數值逼近策略上,然而在濾波過程中除非線性截斷誤差外身的缺陷導致。

在非線性系統的狀態估計過程中,Gustafsson建議單獨研究狀態先驗PDF的預測和濾波更新過程[8-9]。KF濾波的發散問題多出現在量測更新階段,GNSS/INS濾波過程中非線性量測方程導致的穩定性問題更加突出。量測方程的非線性強度和狀態預測誤差直接影響KF更新過程中量測似然函數的逼近精度,而Newton迭代法是解決非線性回歸問題的常用方法[10]。文獻[11]從最優化思想的角度對幾種不同的迭代EKF算法進行了對比分析,結果表明迭代算法較常規EKF濾波結果有更好的精度和一致性。韓萍等人[12]采用迭代的中心差分卡爾曼濾波器估計飛機姿態取得較好效果,但是算法收斂速度受迭代步長影響較大。宋宇等人[13]采用迭代Sigma點逼近策略解決粒子濾波中的粒子退化問題,并將其應用于移動機器人的定位中,結果表明其在系統噪聲較大量測質量較好的情況下較非迭代算法有較大的優勢。上述方法均在迭代量測更新中采用Newton迭代的方法,其在初始誤差較大時的收斂速度有待改善。

本文提出一種基于阻尼Newton法改進的迭代CKF,不同于文獻[14]中的迭代UKF(IUKF),其在狀態先驗分布的預測過程中不重新產生Sigma點,以避免預測誤差協方差陣不正定導致的濾波發散并減少運算量。為改善狀態初始誤差較大時非線性量測更新的穩定性,基于Backtracking線搜索(BLS)優化迭代步長控制系數,加快迭代過程的收斂速度。將上述基于BLS的迭代CKF應用于GNSS/INS緊組合中,數值仿真和跑車實驗驗證了算法的有效性。

1 非線性量測更新

考慮非線性離散系統

(1)

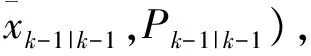
(2)

(3)

(4)

無論是EKF還是Sigma濾波其均做關于p(xk|z1:k-1)的統計線性回歸(SLR)逼近量測似然分布。當p(xk|z1:k-1)誤差較大時,或者量測值較精確時(即后驗PDF較先驗PDF窄很多時)上述SLR方法可能失敗。文獻[11]和文獻[16]采用迭代方法逼近狀態后驗PDF,具有較好的濾波穩定性和精度,然而前者基于線性化逼近p(zk|xk)的框架,非線性較強時容易導致濾波發散,后者的計算復雜度較大且當p(xk-1|z1:k-1)誤差較大時可能會得到不精確的后驗PDF。

2 Sigma點迭代濾波框架

2.1 緊耦合算法

(5)

式中:δr、δv和δψ分別是位置、速度和方向誤差向量,ωen是地理坐標系相對于地球坐標系的旋轉角速度矢量,ωie是地理坐標系相對于慣性坐標系的旋轉角速度矢量,ωin是地理坐標系相對于慣性坐標系的旋轉角速度矢量,f是加速度計測量的比力矢量。加速度誤差向量和陀螺誤差向量ε近似于隨機游走過程模型。

2.2 非線性濾波的最優化思想

獲得k時刻的觀測量Zk后,狀態量的后驗概率密度函數(PDF)可以由式(6)求得:

(6)

即濾波更新的過程等價于最大化后驗PDF的優化問題。由式(6)知其等價于

(7)

采用Newton-Raphson算法處理代價函數V(x)所述的非線性無約束最優化問題有:

xi+1=xi-[2V(xi)]-1V(xi)

(8)

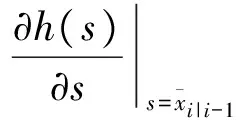
(9)

(10)

代入式(9)并利用矩陣求逆引理得

(11)

由于EKF 未考慮泰勒展開后的高階項,所以其線性化后的非線性量測方程為:

zk=Hkxk|k-1+vk+ξk

(12)

式中:ξk為非線性截斷誤差,存在

(13)

(14)

(15)

2.3 迭代更新優化

在非線性濾波的迭代更新過程中,代價函數V(x)的下降受量測方程非線性的影響較大,適當的選擇步長控制系數αi可以加速并確保V(x)下降。本項目采用BLS優化步長的策略,定義步長S和步長下降量ΔV為:

(16)

基于BLS更新過程是在r∈(0,0.5)、β∈(0,1)條件下計算αi=αiβ直至V(xi+αiSi)≤V(xi)+γαiV(xi)TSi,停止更新得到αi,式(14)所示的Newton迭代過程描述如圖1所示。

由圖1知迭代更新的xi+1并沒有反饋到模型預測過程中,即迭代過程只考慮非線性量測似然方程的SLR,因為非線性濾波器的多數問題都發生在量測更新階段。由于時間更新過程受模型不確定性影響較大,有文獻報道指出在預測誤差的協方差陣Pk|k-1中添加正矩陣ΔQ可以增加濾波器的穩定性,因此將迭代過程反饋到時間更新階段將增大預測過程對系統模型不確定性的敏感性。同時,考慮到組合導航系統方程的非線性較弱,通過使用閉環校正的濾波結構可以減小預測過程的不確定性。

圖1 步長優化的迭代量測更新

3 實驗仿真

為分析 BLS-ICKF算法的有效性分別基于數值仿真和車載實驗進行驗證,值得注意的是文獻[11]中的IEKF和文獻[14]中的IUKF 在迭代過程中等價于固定步長控制系數αi(例如取αi=1)

圖2 αi=1時的迭代量測更新

3.1 數值仿真

圖3 優化αi的迭代量測更新

由圖2可知,αi=1時ICKF和IEKF的迭代更新效果并無區別,而LBS-ICKF在迭代3次后得到V(x)為0.503,x為0.94,其較IEKF得到的0.810和1.10有明顯改善,由于LBS 速度非常快且易實現,將其用于步長控制系數的優化切實可行。值得注意的是當初始狀態值的誤差減小時,如將x0增大10倍,兩種方法具有相似的性能,這主要由于量測方程的非線性較弱,EKF能滿足弱非線性量測似然方程的估計需求。

3.2 車載試驗

陸地車輛導航應用中姿態角的可觀測性較弱,迭代量測更新等價于在當前時刻獲得額外的觀測量,從而改善弱可觀測性狀態的估計精度。車載實驗設備如圖4所示,采用差分方案提高GPS輸出導航參數精度,IMU由閉環干涉型光纖陀螺(IFOG)和MEMS加速度計組成,其中IFOG零偏穩定性小于1 °/h,加速度計零偏穩定性小于1 mgn,參考軌跡為一套NovAtel SPAN系列產品輸出。GNSS/INS組合濾波器采用狀態誤差模型和閉環校正結構,因此系統方程中的非線性誤差可以忽略不計。

圖4 場地實驗設備

需要說明的是,在試驗中利用差分GPS作為組合導航系統的位置基準,其定位誤差小于1 m,系統的結果與其比較得到位置誤差。表1和表2給出了GPS/INS緊耦合和純慣性的導航精度的比較結果。從表中可以看出GPS緊耦合具有很高的精度。

表1 GPS緊耦合最大位置誤差

表2 純慣性最大位置誤差

圖6 航向角和俯仰角的迭代更新

圖5為行車軌跡,其中前半程車輛保持為“8”字形運動,后半程為平穩的直線行駛過程。仿真結果發現迭代停止閾值ε的選擇需根據具體的對象經驗性的調整,且當迭代次數大于3時濾波效果改善較小,因此本文手動設置迭代3次。如圖6所示,BLS-ICKF較CKF提高了航向角和俯仰角的估計精度,當姿態角狀態的可觀測性較好時(頻繁轉彎)迭代量測更新性能優勢不明顯,當車輛直線行駛時迭代量測更新有較好的改進效果。

圖5 場地實驗軌跡

圖7為東向速度的迭代更新結果,可以發現其精度并沒有得到改善,北向速度估計也得到類似的結果。姿態誤差以及IMU誤差屬于不可直接觀測的狀態量,其誤差校正量的估計是通過系統模型耦合實現,即在時間更新過程利用估計誤差協方差矩陣Pk-1|k-1的非對角線元素實現不可直接觀測狀態誤差的校正。

圖7 東向速度的迭代更新

BLS-ICKF和CKF的性能對比如表3所示。表3為BLS-ICKF和CKF這兩種方法的時間消耗和濾波結果的均方誤差(10次仿真結果的均值),從表中可以發現BLS-CKF犧牲較小的時間復雜度顯著,大大改善了車輛航向角的估計精度,但是迭代更新無法減小速度估計誤差。

表3 BLS-ICKF和CKF的性能對比

4 結論

基于Backtracking線搜索實現了一種改進的迭代CKF算法,提出了一種簡化的迭代量測更新框架并將其應用GNSS/INS緊組合中。數值仿真和跑車實驗結果表明,BLS-CKF在初始誤差較大時較常規的迭代UKF和迭代EKF有更快的收斂速度,EKF和 CKF在處理弱非線性的量測更新中具有相似的性能。將BLS-CKF應用于存在弱可觀測狀態量的車載導航狀態估計,BLS-CKF犧牲較小的時間復雜度得到航向角誤差約為CKF估計的 41%。下一步工作將基于狀態估計誤差的檢測,建立迭代更新方法的約束模型,并針對控制系數。

[1] Julier S J,Uhlman J K,Durrant-Whyte H F. A New Approach for Filtering Nonlinear Systems[C]//Proceedings of the American Control Conference. Washington,USA:IEEE,1995:1628-1632.

[2] Arasaratnam I,Haykin S. Cubature Kalman Filters[J]. IEEE Trans Autom Control,2009,54(6):1254-1269.

[3] Crassidis J L. Sigma-Point Kalman Filtering for Integrated GPS and Inertial Navigation[J]. IEEE Trans Aerosp Electron Syst,2006,42(2):750-756.

[4] Wendel J,Metzger J,Moenikes R,et al. A Performance Comparison of Tightly Coupled GPS/INS Navigation Systems Based on Extended and Sigma Point Kalman Filters[J]. Navigation:Journal of the Institute of Navigation,2006,53(1):21-31.

[5] 侯當云,呂偉杰. 基于偏差迭代的干擾源定位算法[J]. 傳感技術學報,2015,28(12):1818-1822.

[6] Zhao Y W. Performance Evaluation of Cubature Kalman Filter in a GPS/IMU Tightly-Coupled Navigation System[J]. Signal Processing,2016,119:67-79.

[7] Morelande M R,Garcia-FernndezF. Analysis of Kalman Filter Approximations for Nonlinear Measurements[J]. IEEE Transactions on Signal Processing,2013,61(22):5477-5484.

[8] 劉栓,宋喜忠. 基于可信度估計的迭代濾波的WSNs數據融合算法[J]. 電子器件,2016,39(4):810-815.

[9] Gustafsson F,Hendeby G. Some Relations between Extend and Unscented Kalman Filters[J]. IEEE Transactions on Signal Processing,2012,2(60):545-555.

[10] 龐鴻鋒,潘孟春,王偉,等. 基于高斯牛頓迭代算法的三軸磁強計校正[J]. 儀器儀表學報,2013,34(7):1507-1511.

[11] Skoglund M A,Hendeby G,Axehill D. Extended Kalman Filter Modifications Based on an Optimization View Point[C]//18th International Conference of Information Fusion,2015.

[12] 韓萍,干浩亮,何煒琨,等. 基于迭代中心差分卡爾曼濾波的飛機姿態估計[J]. 儀器儀表學報,2015,36(1):187-193.

[13] 宋宇,孫富春,李慶玲. 移動機器人的改進無跡粒子濾波蒙特卡羅定位算法[J]. 自動化學報,2010,36(6):851-857.

[14] Zhan R H,Wang J W. Iterated Unscented Kalman Filter for Passive Target Tracking[J]. IEEE Tran on Aerospace and Electronic Systems,2007,43(3):1155-1163.

[15] Ito K,Xiong K Q. Gaussian Filters for Nonlinear Filtering Problems[J]. IEEE Trans Autom. Control,2000,45(5):910-927.

[16] García-FernndezF,Svensson L,Morelande M R,et al. Posterior Linearization Filter:Principles and Implementation Using Sigma Points[J]. IEEE Transactions on Signal Processing,2015,63(20):5561-5573.

[17] Xiong K Q,Zhang H Y,Chan C W. Performance Evaluation of UKF-Based Nonlinear Filter[J]. Automatica,2006,42:261-270.

ImprovedIteratedCubatureKalmanFilterandItsApplicationtoTightlyCoupledGlobalNavigationSatelliteSystem/InertialNavigationSystem

HUAXuehui*,CHENDali

(Foshan Polytechnic Institute,Foshan Guangdong 528000,China)

To improve the stability and accuracy of nonlinear filter used in tightly coupled GNSS/INS,a novel iterated cubature Kalman filter(CKF)is proposed based on backtracking line search(designated as BLS-ICKF). First,a generalized iterated framework is developed,and a damped Newton method is used to improve filtering accuracy with large initial state error. Moreover,a simplified iterated update structure is proposed to improve the robustness of prediction process for integrated system. Numerical simulations and field test reveal that,compared with CKF,BLS-ICKF improves the heading accuracy by 59% in terms of mean square error,and has a faster convergence rate than traditional iterated filtering method.

integrate navigation;iterated filtering framework;cubature Kalman filter;backtracking line search

10.3969/j.issn.1005-9490.2017.05.026

2016-08-04修改日期2016-09-24

TP273;TH89

A

1005-9490(2017)05-1185-06

化雪薈(1976-),女,甘肅景泰人,碩士,高級實驗師,主要從事應用電子設計、移動通信技術、傳感器應用方向的研究,huaxuehui_vip@163.com;

陳大力(1975-),男,吉林四平人,副教授,主要從事工業控制、電子設計方面研究。