基于雙沖擊特征的無轉速計混合陶瓷球軸承剝落區寬度估計

康 偉， 郭 瑜， 伍 星

(昆明理工大學 機電工程學院 云南省高校振動與噪聲重點實驗室，昆明 650500)

基于雙沖擊特征的無轉速計混合陶瓷球軸承剝落區寬度估計

康 偉， 郭 瑜， 伍 星

(昆明理工大學 機電工程學院 云南省高校振動與噪聲重點實驗室，昆明 650500)

首先介紹了一種基于振動信號分析的滾動球軸承剝落區寬度估計的方法，該方法可根據振動信號中的雙沖擊特征間隔和所在轉軸的轉速，完成對剝落區寬度的估計，但轉速計的安裝易受工況條件的限制，對此提出了一種基于滾動軸承剝落故障對應沖擊特征的無轉速計剝落區寬度估計方法，該方法通過振動信號中整周期的沖擊次數實現轉速估計,結合平均雙沖擊特征實現了無需轉速計的混合陶瓷球軸承的剝落區寬度估計，使該方法更適合于工程應用。試驗結果表明，所提方法可對混合陶瓷球軸承剝落區寬度進行有效估計。

剝落；混合陶瓷球軸承；雙沖擊特征

混合陶瓷(Si3N4)球軸承[1]在高速電主軸中得到廣泛應用，其故障為高速電主軸失效的主要形式之一。因此，開展混合陶瓷球軸承故障特征提取和故障診斷研究有重要意義。同常規滾動球軸承類似，混合陶瓷球軸承的主要失效形式也是疲勞剝落[2]。值得注意的是，滾動軸承故障程度的大小可由剝落區寬度來反映，但對剝落區寬度的測量，目前可用的方法有限，通常只能將軸承拆卸后進行測量，操作不便。近來，一種基于振動信號分析的滾動球軸承剝落區寬度估計的方法[3]被提出，即通過提取故障信號中的雙沖擊特征，獲取雙沖擊之間的時間間隔，再結合轉速，實現對剝落區寬度的測量。該方法的提出，為實現運行工況下的剝落區寬度估計提供了可能。以外圈剝落故障為例，當滾動體通過外圈剝落區時，在進入點和退出點均會產生相應的沖擊，形成雙沖擊特征[4]。Sawalhi等[5]提出了一種基于最小熵解卷積(MED)濾波的故障特征增強方法，對滾動球軸承故障雙沖擊特征的提取有較好的效果。本文結合上述方法，研究介紹了一種基于振動信號分析的滾動球軸承剝落區寬度估計的方法。需要指出的是，該方法不僅需要采集振動信號，還需要采集實時轉速信號。但實際工況中，受安裝條件等限制，轉速信號的獲得不能得到保證，影響了該方法的工程應用。針對上述不足，本文提出了一種基于沖擊特征的無轉速計剝落區寬度估計方法。以人造故障混合陶瓷球軸承為試驗對象，分別使用Randall剝落區寬度估計方法和新方法對剝落區寬度進行估計，結果表明，所提方法可對剝落區寬度進行有效估計。

1 滾動軸承剝落故障雙沖擊特征

1.1 雙沖擊特征簡介

滾動軸承剝落故障雙沖擊特征由Epp發現，描述的是具有外圈(或內圈)剝落故障的滾動軸承在運行時，滾動體通過剝落區所產生的一種固有現象。之后Dowling[6]和Randall都對其進行了相關研究，進一步驗證了雙沖擊特征的存在。但是，在雙沖擊特征的構成上，Epp認為其由一個階躍響應和一個脈沖響應構成，郭瑜等[7]則認為其由兩個脈沖響應構成，Randall通過對外圈剝落故障滾動球軸承振動信號的雙沖擊特征分離提取的研究，得出了與Epp更加近似的觀點，即：雙沖擊特征由一個階躍響應和一個脈沖響應所構成。以外圈故障為例，如圖1所示，雙沖擊特征產生原理可解釋為：假設軸承外圈固定，內圈跟隨轉軸做順時針轉動，當滾動體進入剝落區前邊緣時，通過剝落區的滾動體的旋轉中心變為A點，滾動體與滾道間發生非瞬時的去應力，產生一階躍響應；當滾動體經過剝落區一半時，通過剝落區的滾動體的旋轉中心由A點變為B點，其回轉方向也同時發生改變，滾動體對剝落區后邊緣產生突然地瞬時沖擊，產生一脈沖響應；當滾動體完全通過剝落區時，又恢復正常承載狀態。然而，振動信號中的雙沖擊特征由于受到噪聲和信號衰減的影響，難以直接觀察，須通過信號處理方法進行分離和提取，才能清晰獲得。

圖1 外圈剝落故障引起雙沖擊特征示意Fig.1 Double impulses illusion causedby the spall of bearing outer ring

1.2 雙沖擊特征提取

當滾動軸承存在外圈(或內圈)剝落故障的時候，其滾動體在通過故障區時會產生周期性雙沖擊特征，可激起軸承及其周圍結構的固有振動。振動信號中的雙沖擊特征，由于受到傳遞路徑和環境中的強噪聲影響，不易直接在原始振動信號中進行觀察。利用基于最小熵解卷積(MED)濾波的故障特征增強方法可有效提取雙沖擊特征，其基本步驟如圖2所示。

圖2 雙沖擊特征提取原理框圖Fig.2 Extraction procedure of double impulses

首先，使用AR預白化的方法處理原始信號，去除振動信號中的確定性信號的干擾，得到包含明顯故障特征的殘余信號。該過程可用下式表示

(1)

式中：εk為含有故障特征的殘余信號；p為AR模型的階次(階次大小可根據峭度原則確定[8])；ai為AR模型的參數；x為振動信號，下標k表示第k點。

其次，使用結合譜峭度的MED濾波方法對殘余信號做進一步處理，解卷積傳遞路徑的影響，獲取顯著抑制頻帶外噪聲干擾影響的振動信號(由于本文主要是估計剝落區寬度，故對該方法不做詳細介紹，詳情可參見文獻[5])。

最后，使用基于Hilbert變換的包絡提取方法對信號進行解調，獲取包絡信號并提取信號的雙沖擊特征。

2 剝落區寬度估計

滾動軸承的疲勞效應會引發其滾道或滾動體的剝落，進而導致滾動軸承的失效。在實際生產中，滾動軸承在發生剝落故障的初期，仍可繼續工作一段時間，若過早對滾動軸承進行維護和更換，將增加生產成本。因此，開展研究一種有效的故障評測方法有重要意義。

2.1 基于雙沖擊特征的剝落區寬度估計方法

美國NASA通過檢測潤滑油中的碎屑來評判滾動軸承的故障發展程度[9]，取得了一定的效果，但也存在造價高昂等不足之處，不利于工程運用。剝落區寬度的大小可反映軸承損傷的劇烈程度，對軸承剩余壽命的預測十分重要。Randall研究完善了雙沖擊特征的相關理論，并把雙沖擊特征用于剝落區寬度的估計當中，提出了基于振動信號雙沖擊特征的剝落區寬度估計方法，可有效估計剝落區寬度大小。

由雙沖擊特征的形成原理可知，據雙沖擊特征所計算的時間間隔實際上只是滾動體通過剝落區寬度一半時所用的時間。Randall指出，剝落區寬度l0(mm，如圖1所示)與雙沖擊間隔Ti(單位為點，注：采樣率一定的情況下，采樣時刻t所對應的點數是確定的，為便于表示，文中直接使用采樣點數表示其對應的采樣時刻，故雙沖擊間隔既為對應的脈沖響應時刻與階躍響應時刻之間的間隔點數)存在如下關系

(2)

式中：fr是轉軸的轉速，Hz；fs是采樣頻率，Hz；Dp是滾動軸承的節圓直徑，mm；d是滾動軸承滾動體的直徑，mm。

上述關系式的形成可由以下步驟實現(以外圈剝落故障為例)。

外圈故障剝落區寬度為l0(mm)的滾動軸承，單個滾動體通過剝落區的時間t(s)可以表示為

(3)

式中：D0是滾動軸承的外滾道直徑，mm；fc是保持架的轉速，Hz。

外滾道直徑D0可寫成如下形式

D0=Dp+d

(4)

式中：Dp是滾動軸承的節徑，mm。

保持架的轉速fc(即：滾動體的公轉速度)可按下式計算[10]

(5)

式中：α是滾動體與內外滾道的夾角；fi是滾動軸承內圈的轉速，Hz；fo是滾動軸承外圈的轉速，Hz。

假設滾動軸承的接觸角α=0°，且外圈固定，內圈跟隨轉軸轉動，則保持架的轉速為

(6)

將式(2)與式(6)代入式(3)可得滾動體通過剝落區的時間t，如下所示

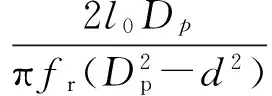
(7)

振動信號中，采樣點數Ts與采樣時刻t存在如下關系

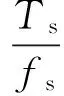
(8)

由于剝落區寬度對應的采樣點數Ts為雙沖擊間隔點數Ti的兩倍，故整理式(7)可得

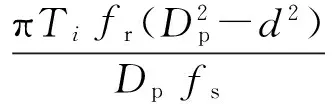
(9)

2.2基于雙沖擊特征的無轉速計剝落區寬度估計方法

由Randall提出的剝落區寬度估計方法可知：在對滾動球軸承剝落區寬度進行估計時， 除了計算雙沖擊特征間隔外，還需要測量轉軸的轉速。上文已經提到，受限于工況條件，轉速計安裝受到限制，不利于該方法的工程應用。因此，本文提出了一種基于雙沖擊特征的無轉速計剝落區寬度估計方法。

(1)雙沖擊特征間隔的選取：根據以上提到的雙沖擊特征提方法，能有效分離提取振動信號中的雙沖擊特征。但考慮到選取雙沖擊間隔時間時，需克服偶然因素的影響，取多個雙沖擊特征間隔時間的平均值更加合理。但多個雙沖擊間隔的提取存在計算量大這一不足，針對這一問題，本文提出了一種半自動的雙沖擊特征間隔選擇方法，幫助快速選取包絡信號中的雙沖擊特征時間間隔。具體實施過程如下：首先，通過一個脈沖響應閾值，將包絡信號中的所有脈沖響應特征挑選出來，因為脈沖響應比階躍響應更加明顯；其次，為避免包絡信號中脈沖響應特征前后存有干擾階躍響應特征的峰值信號，需在脈沖響應特征前將部分信號置零和脈沖響應特征后將部分信號置零；最后，設定一階躍響應閾值，對置零操作后的包絡信號進行雙沖擊特征間隔提取。

(2)無轉速計剝落區寬度估計： 首先，使用基于MED的雙沖擊特征增強方法對原始振動信號中的雙沖擊特征進行增強，獲取雙沖擊特征明顯的振動信號。

然后，根據雙沖擊特征信號，利用上文提到過的雙沖擊特征間隔選取方法提取信號中的雙沖擊特征位置信息，計算平均雙沖擊特征間隔和滾動軸承旋轉一圈的時間間隔。當滾動軸承存在外圈剝落故障時，任意一個滾動體沿外滾道滾過一圈時，其余滾動體也將沿外滾道滾過一圈，在此過程中，一共會產生N個雙沖擊特征。圖3中，ai(i=1,2,…,N)表示雙沖擊特征中的第i個階躍響應特征，bi(i=1,2,…,N)表示雙沖擊特征中的第i個脈沖響應特征。因此，滾動軸承旋轉一圈所用時間可表示為第i個脈沖沖擊響應時間與第i+N個脈沖沖擊響應時間的間隔(或第i個階躍沖擊響應時間與第i+N個階躍沖擊響應時間的間隔)，由于脈沖響應比階躍響應更加明顯且更易提取，故選取脈沖響應時間計算滾動軸承旋轉一圈的時間。

最后，根據下式計算剝落區寬度，完成故障剝落區寬度的估計。

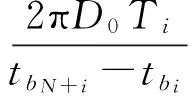
(10)

式中：tbi(i=1,2,…,N)為雙沖擊特征中脈沖響應特征對應的采樣點數；N為滾動軸承的滾動體個數。式(10)的推導過程如下。

滾動軸承外圈故障剝落區寬度l0(mm)與外圈滾道周長之比c可表示為

(11)

滾動體沿滾動軸承外滾道轉過一圈所產生的雙沖擊間隔均值與轉動一圈所用時間的比值c1可表示為

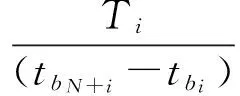
(12)

根據雙沖擊特征間隔點數Ti為滾動體通過剝落區寬度一半的時間，可得如下等式

c=2×c1

(13)

將式(11)與式(12)代入式(13)并整理得，滾動軸承外圈故障剝落區寬度l0(mm)與雙沖擊特征時間間隔(點數)存在以下的關系

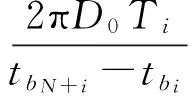
(14)

由式(14)可以看出，該方法完全基于振動信號中的雙沖擊特征估計剝落區寬度，無需安裝轉速計，易于工程應用。上述無轉速計剝落區寬度估計方法可用原理框圖4表示。

圖4 無轉速計剝落區寬度估計原理框圖Fig.4 Evaluation procedure of spall size without speed meter

3 試驗驗證

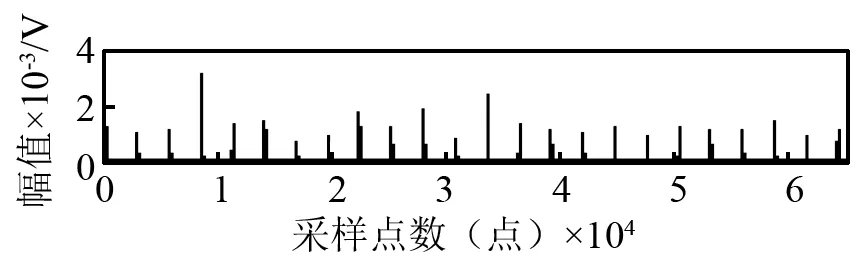
本文采用QPZZ-Ⅱ型故障模擬試驗臺(如圖5所示)對外圈剝落故障混合陶瓷球軸承進行振動分析試驗，試驗參數如下：故障軸承型號為6205，外圈故障尺寸分別為1.237 mm、2 mm和2.16 mm(以故障尺寸為1.237 mm的混合陶瓷球軸承為例，如圖6所示)；安裝軸轉速：646.75 r/min；數據采集設備為NI USB9215，采樣率為100 kHz；加速度傳感器型號為DH112，靈敏度為5.33 pC/(m·s-2)，安裝位置為軸承座。試驗所采集原始振動信號如圖7所示。

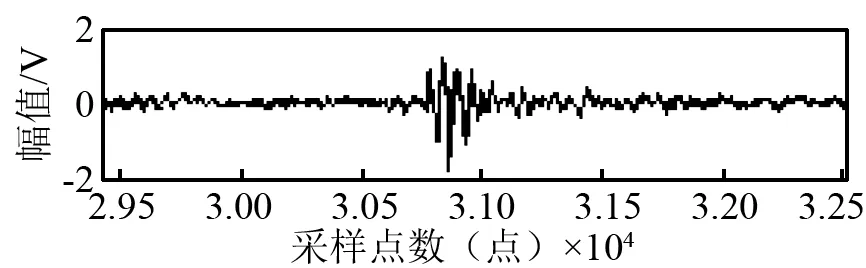
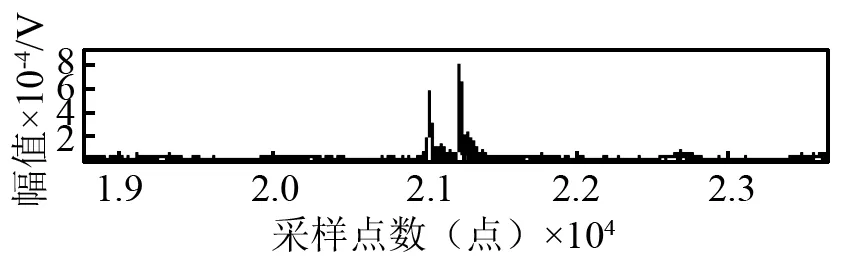
首先，對采集到的原始振動信號首先進行雙沖擊特征提取，得到圖8所示的雙沖擊特征包絡信號。任意選取其中一個雙沖擊特征進行局部放大，得到圖9所示的局部放大原始振動信號和圖10所示的局部放大雙沖擊特征信號，由圖10可得，不同外圈故障尺寸的雙沖擊特征均被有效提取。

然后，利用上文中提出的雙沖擊特征間隔選取方法從雙沖擊特征包絡信號中提取雙沖擊時間間隔，并將對應的階躍響應點和脈沖響應點表示出來，如表1、表2和表3所示(注：各表中，采樣時刻和雙沖擊特征間隔單位為點)。

圖5 QPZZ-Ⅱ型試驗臺Fig.5 QPZZ-Ⅱ test rig

圖6 1.237 mm剝落故障混合陶瓷球軸承外圈Fig.6 Hybrid ceramic ballbearing outer race withthe fault size 1.237 mm

(a) 1.237 mm外圈故障

(b) 2 mm外圈故障

(a) 1.237 mm外圈故障

(b) 2 mm外圈故障

(c) 2.16 mm外圈故障圖8 雙沖擊特征包絡信號Fig.7 Double impulses envelope signal

(a)1.237 mm外圈故障

(b) 2 mm外圈故障

(c) 2.16 mm外圈故障圖9 原始振動信號局部放大Fig.9 The local amplification of raw vibration signal

(a)1.237 mm外圈故障

(b)2 mm外圈故障

(c)2.16 mm外圈故障圖10 雙沖擊特征信號局部放大Fig.10 The local amplification of double impulses envelope signal表1 1.237 mm外圈故障雙沖擊特征信息提取Tab.1 Double impulse information extractionof 1.237 mm outer race faults

階躍響應時刻tai脈沖響應時刻tbi雙沖擊特征時間間隔Tii=15664576399i=28465855893…………i=9279032799794i=10306963078690

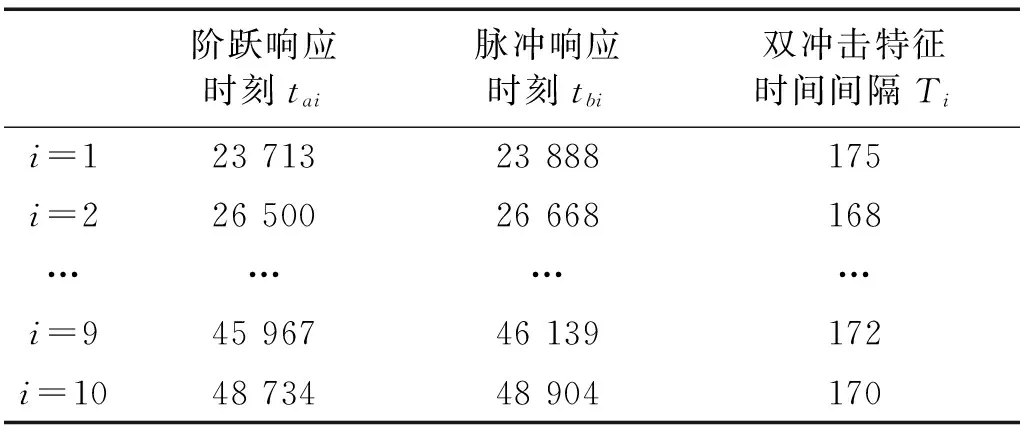
表2 2 mm外圈故障雙沖擊特征信息提取Tab.2 Double impulse information extractionof 2 mm outer race faults

表3 2.16 mm外圈故障雙沖擊特征信息提取Tab.3 Double impulse information extractionof 2.16 mm outer race faults

最后，利用Randall估算公式和新提出的估算公式分別對滾動軸承的剝落區寬度進行預估。計算結果如表4、表5和表6所示(注：各表中，Ti為雙沖擊特征間隔，單位：點；fr為轉軸轉速，單位：Hz；剝落區寬度尺寸單位：mm)。

表4 1.237 mm外圈故障剝落區寬度預估結果Tab.4 Spall size calculation of 1.237 mm outer race faults

表5 2 mm外圈故障剝落區寬度預估結果Tab.5 Spall size calculation of 2 mm outer race faults

表6 2.16 mm外圈故障剝落區寬度預估結果Tab.2 Spall size calculation of 2.16 mm outer race faults

試驗結果表明，Randall剝落區寬度估計方法和新方法均能完成故障混合陶瓷球的剝落區尺寸估計，但新方法并不需要安裝轉速計。

4 結 論

針對滾動軸承剝落區大小難以有效在線提取這一問題，本文介紹了Randall剝落區寬度預估方法，并針對工況中滾動軸承所在轉軸速度不便測量這一不足，提出了一種無轉速計的剝落區寬度預估方法。以外圈人工故障混合陶瓷球軸承作為實驗對象，利用Randall剝落區寬度預估方法和新提出的剝落區寬度預估方法同時對該故障剝落區進行寬度估計，結果表明所提方法與原方法一樣有效，但新方法避免了轉速計安裝，更加適合于工程應用。

[1] 蔣喜，劉宏昭. 混合陶瓷球軸承的選型研究[J]. 西安理工大學學報，2012，28(1)： 33-38.

JIANG Xi, LIU Hongzhao. Selection of the hybrid ceramic ball bearings[J]. Journal of Xi’an University of Technology, 2012, 28(1): 33-38.

[2] 蔣喜，吳國慶，陳曉陽. 氮化硅陶瓷球滾動接觸疲勞壽命模型[J]. 機械工程學報，2008，44(2)： 37-42.

JIANG Xi, WU Guoqing, CHEN Xiaoyang. Tensile stress life model for rolling contact fatigue of silicon nitride ceramic balls [J]. Chinese Journal of Mechanical Engineering, 2008, 44(2): 37-42.

[3] SAWALHI N, RANDALL R B. Vibration response of spalled rolling element bearings: observations, simulations and signal processing techniques to track the spall size[J]. Mechanical Systems and Signal Processing，2011，25(3)： 846-870.

[4] EPPS I K. An investigation into vibrations excited by discrete faults in rolling element bearings[D]. Christchurch:The University of Canterbury, 1991.

[5] SAWALHI N, RANDALL R B, ENDO H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J]. Mechanical Systems and Signal Processing，2007，21(6)： 2616-2633.

[6] DOWLING M J. Application of non-stationary analysis to machinery monitoring[J]. IEEE International Conference on Acoustics, 1993, 1： 59-62.

[7] 郭瑜，鄭華文，高艷，等. 基于譜峭度的滾動軸承包絡分析[J]. 振動、測試與診斷，2011，31(4)： 517-521.

GUO Yu, ZHENG Huawen, GAO Yan,et al. Envelop analysis of rolling bearing based on spectral kurtgoram[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 517-521.

[8] ENDO H, RANDALL R B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]. Mechanical Systems and Signal Processing, 2007, 21: 906-919.

[9] DEMPSEY P J, CERTO J M, MORALES W. Current status of hybrid bearing damage detection[J]. Tribology Transactions, 2005, 48(3): 370-376.

[10] 楊國安. 機械設備故障診斷實用技術叢書 滾動軸承故障診斷實用技術[M]. 北京：中國石化出版社，2012.

Spallsizeestimationoffaultyhybridceramicballbearingswithoutaspeedmeterbasedondoubleimpulses

KANG Wei, GUO Yu, WU Xing

(Key Lab. of Vib. & Noise under Ministry of Education of Yunnan Province, Faculty of Mechanical and Electrical Engineering,Kunming University of Science and Technology, Kunming 650500, China)

A method based on vibration signal was introduced for evaluating the spall size of rolling ball bearings, which utilizes the interval measurement of double impulses generated by the spall and the rotor speed of the bearing mounted shafts. However, the measurement of rotor speed is not convenient under some working conditions. To solve this issue, a method based on double impulses was proposed without a speed meter. The rotor-speed estimated by counting the number of impulses in a full rotating cycle of the shaft. By combining the rotor speed and average double-impulse intervals, the new method realizes spall size estimation without a speed meter. It is thus appropriate for engineering applications. Experimental results indicate that the proposed method is valid.

spall; hybrid ceramic ball bearing; double impulses

國家自然科學基金(51365023)

2016-06-15 修改稿收到日期： 2016-08-30

康偉 男，碩士生, 1992年生

郭瑜 男, 教授，博士生導師, 1971年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.20.001