A FUNDAMENTAL THEOREM ON F-SPACES AND ITS APPLICATION IN NUMERICAL ANALYSIS
DU Nai-lin,XIA Wei
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
A FUNDAMENTAL THEOREM ONF-SPACES AND ITS APPLICATION IN NUMERICAL ANALYSIS
DU Nai-lin,XIA Wei
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
The main results of this paper are Theorems 1.1 and 1.2 in Section 1.Theorem 1.1 may be regarded as the basic tool in the theory ofF-spaces,for it implies fundamental principles such as the uniform boundedness theorem,the open mapping theorem,and the closed graph theorem.Theorem 1.2 can be viewed as an application of Theorem 1.1 in numerical analysis,which shows that an abstract approximation scheme(consisting of a sequence of closed operators with closed ranges inF-space setting)is convergent if and only if it is stable.
F-space;closed linear operator;convergence;stablity
1 Introduction and Main Results
The uniform boundedness theorem,the closed graph theorem and the open mapping theorem are usually referred to as fundamental principles in functional analysis(see e.g.[5]).In this paper,based upon the Baire-Hausdor fftheorem,we prove a theorem which contains the above principal theorems as its simple corollaries(see Theorem 1.1).As a more profound application of the theorem,a useful result in numerical analysis is established,which may be viewed as an abstract generalization of the well-known Lax-Richtmyer equivalene theorem[3](see Theorem 1.2).
We need to recall the de finition ofF-spaces and to illustrate the notation used in the paper.A linear spaceXis called a quasi-normed linear space,if for everyx∈Xthere is associated areal number‖x‖,the quasi-norm of the vectorx,which satisfies

A quasi-normed linear spaceXis called anF-space if it is complete.Next,letXbe anF-space.For a pointx∈Xand areal numberr>0,byBX(x,r)we denote the open ball inXwith the center atxand the radiusr,namely,
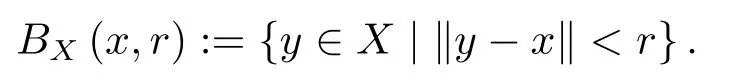
For a subsetAofX,let the symbolsA°anddenote the interior and the closure ofArespectively.The setAis said to be bounded if it is absorbed by any open ballBX(0,ε)with center at 0,i.e.,if there exists a positive constantαsuch thatα?1A?BX(0,ε),where
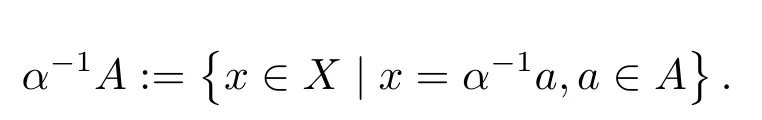
For a sequence of nonempty subsets{An}ofX,we set
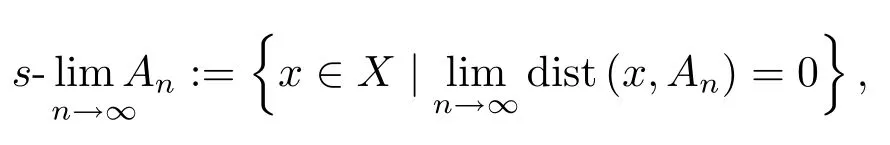
where
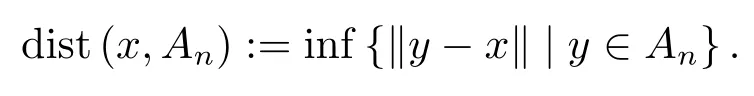
Now,letYbe anF-space on the same scalar field as theF-spaceX,T:D?X→Ya linear mapping from the subspaceDofXintoY.ByD(T),R(T),N(T)andG(T),we denote the domain,the range,the null space,and the graph ofT,respectively,i.e.,
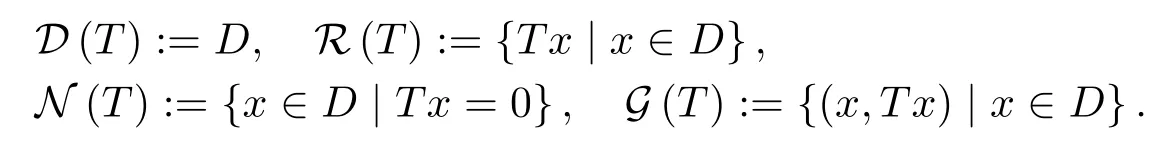
For any∈Y,the preimage of the pointyis denoted byT?1(y),namely,
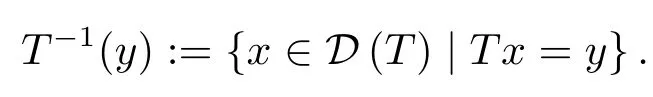
In addition,X×Yis also anF-space by the algebraic operations
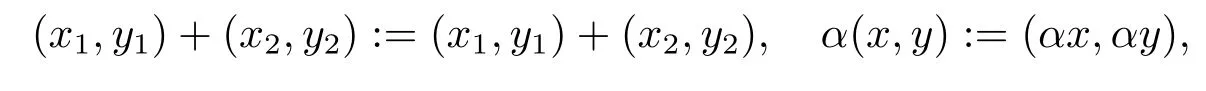
and the quasi-norm
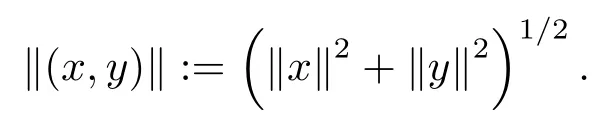
The main results in this paper are the two following theorems.
Theorem 1.1LetXbe anF-space.Letp:X→R be areal-valued function onXwith the following properties:
a)p(x)≥0 for allx∈X(nonnegativity);
b)p(?x)=p(x)for everyx∈X(symmetry);
Theorem 1.2LetXandYbeF-spaces.Let{Tn:D(Tn)?X→Y}be a sequence of closed operators with closed ranges.Then the following three properties of{Tn}are equivalent:
A)ifxn∈D(Tn)(n∈N)with
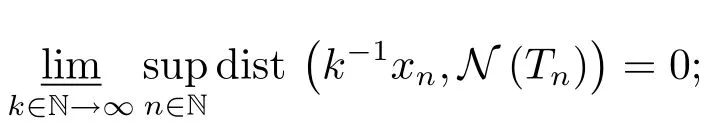
B)for everyε>0 there exists aδ>0 such that
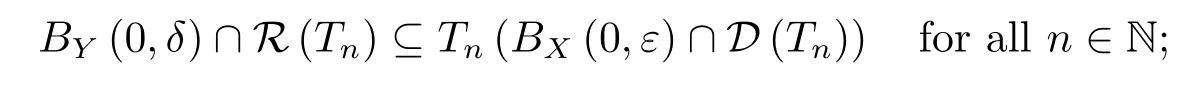
C)ifyn∈R(Tn)(n∈N)with
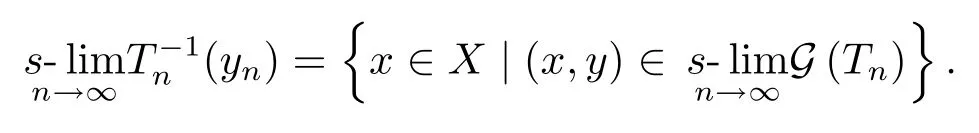
Theorem 1.1 may be regarded as the basic tool in the theory ofF-spaces,for it implies some fundamental principles as simple corollaries,such as the uniform boundedness theorem,the open mapping theorem,and the closed graph theorem.It must be noted that Theorem 1.1 contains Theorem 1.2 as a more profound application.
Theorem 1.2 can be interpreted as a generalization of the well-known Lax-Richtmyer equivalence theorem[3](which states that,for linear well-posed initial value problems,a consistent difference scheme is convergent if and only if it is stable):for an oprater equation of the first kindTx=y,whereT:D(T)?X→Yis a closed linear operator,we assume that the equation is with a consistent approximation scheme{Tn}as given in Theorem 1.2,here“consistent”means
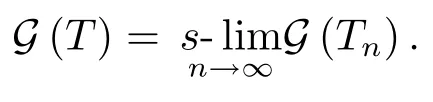
Then condition A or B stands for stability of the scheme{Tn},condition C stands for convergence of{Tn},and the conclusion is
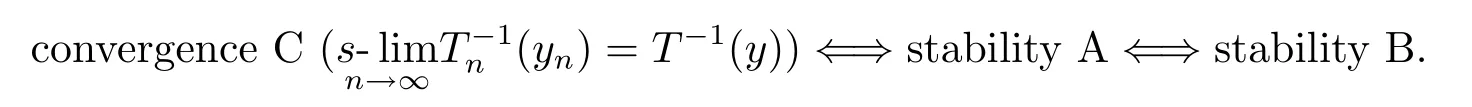
This is also a generalization of[1,Theorem 2.1]and[2,Theorem 1].
The paper is organized as follows:in Section 2,we present the proof of Theorem 1.1,and in Section 3,we show that some fundamental principles as simple corollaries of the theorem.In Section 4,we present the proof of Theorem 1.2 with remarks and examples of application.
2 The Proof of Theorem 1.1
We recall the Baire-Hausdor fftheorem before proving Theorem 1.1:A non-void complete metric space is of the second category(see,e.g.,[5]).As is well known,the completeness of anF-space enables us to apply the Baire-Hausdor fftheorem and to obtain such fundamental principles in functional analysis as the uniform boundedness theorem,the closed graph theorem and open mapping theorem.Here,we are to apply the Baire-Hausdor fftheorem to establish a more general principle,Theorem 1.1.
Proof of Theorem 1.1The proof is to be carried out in three steps.
Step 1Prove that for anyε>0 there exists a sequence{δn}of positive real numbers such that
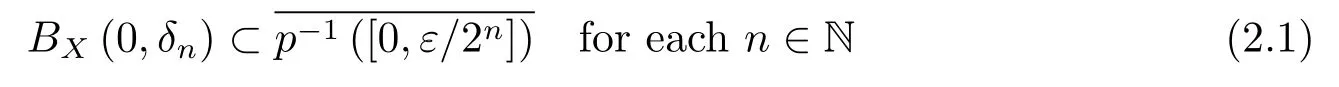
and

It is obvious by properties a)and c)ofpthat
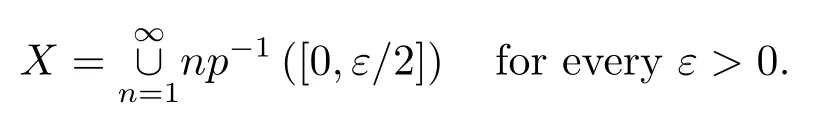
SinceXis a non-void complete metric space,Xis of the second category by the Baire-Hausdor fftheorem,so that there must be a natural numberksuch thatHence,there existx0∈Xandr>0 such that
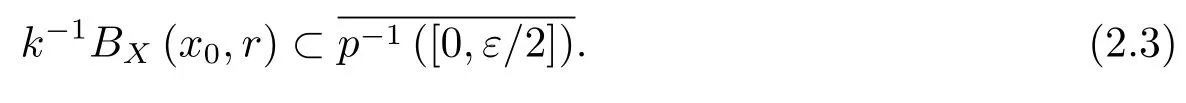
Note that,by properties b)and d)ofp,the setis with the following two properties
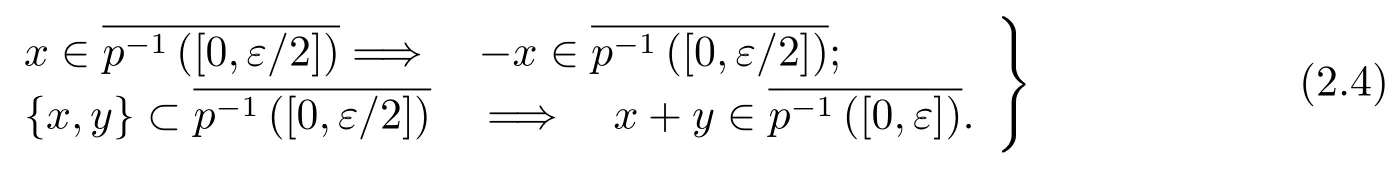
Therefore from(2.3)and(2.4),we obtainThus for everyε>0,there existsδ>0 such that

From(2.5),we obtain that for anyε>0 there exists a sequence{δn}of positive real numbers such that(2.1)and(2.2)hold.
Step 2Prove that for anyε>0 there existsδ>0 such that

By the conclusion of Step 1,for anyε>0 there exists a sequence{δn}of positive real numbers such that(2.1)and(2.2)hold.Letδ=δ1andx∈BX(0,δ).Then we have thatfrom(2.1),and hence there existssuch that‖x?x1‖ <δ2,i.e.,x?x1∈B(0,δ2).Assumen≥1 and(k=1,···,n)are chosen to satisfy
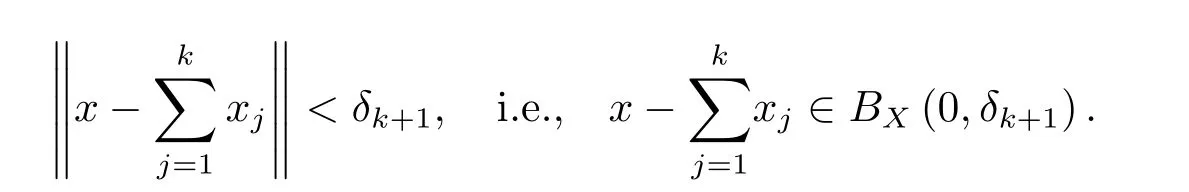
Then by(2.1),there existsxn+1∈p?1([0,ε/2n+1])such that
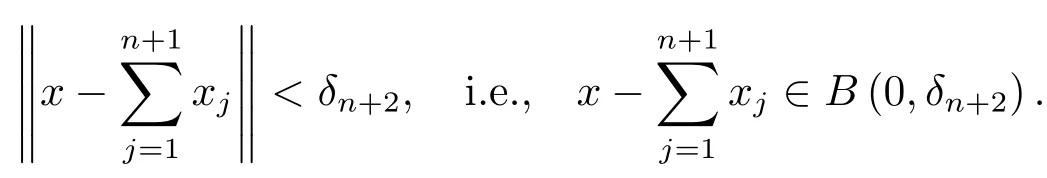
Thus we obtain a sequence{xn}ofXsuch that

and
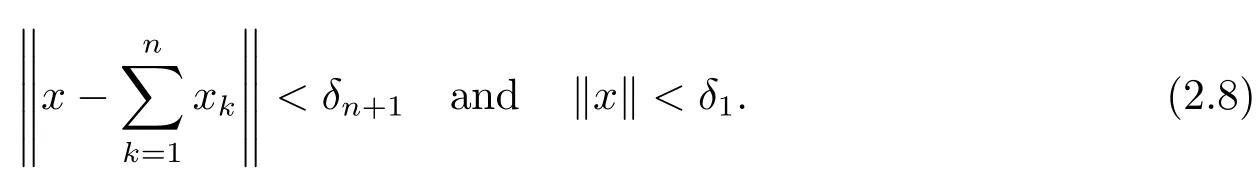
Note that(2.8)with(2.2)implies that
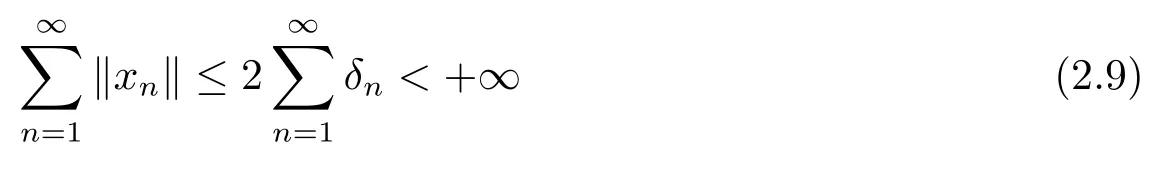
and

Therefore,from(2.7),(2.9),(2.10),and the property d)ofp,we conclude that
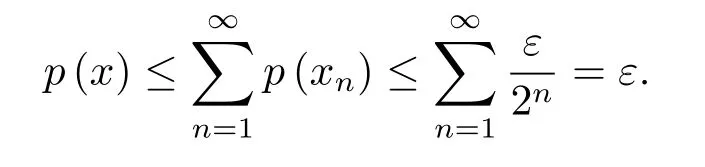
Thus(2.6)follows.
Step 3Prove thatpis continuous onX,we need only to show thatpis continuous at 0.This is obviously true by the conclusion of Step 2.
3 Simple Corollaries of Theorem 1.1
In this section,we will see that the uniform boundedness theorem,the closed graph theorem,and the open mapping theorem can be proved as simple corollaries of Theorem 1.1.In order to emphasize the role of Theorem 1.1,the above three theorems are stated in a little more generality than is usually needed.By doing that,we get more interesting versions.
Corollary 3.1(The Uniform Boundedness Theorem)LetXbe anF-space,Ya quasinormed linear space and{Tλ}λ∈Λa family of continuous mappings de fined onXintoY.Assume that
1)‖Tλ(x+y)‖ ≤ ‖Tλ(x)‖+‖Tλ(y)‖for anyλ ∈Λ andx,y∈X,and
ProofBy Assumption 1),we have

Therefore,by Assumption 2),we obtain
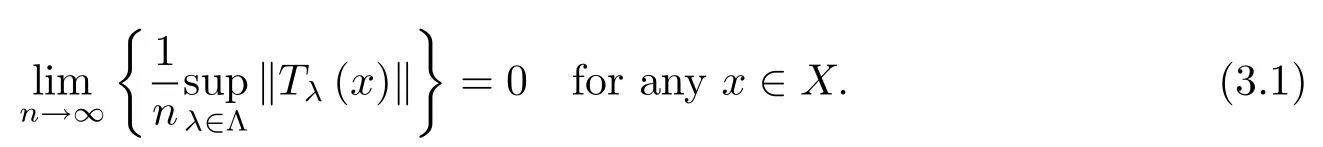
It follows from(3.1)that
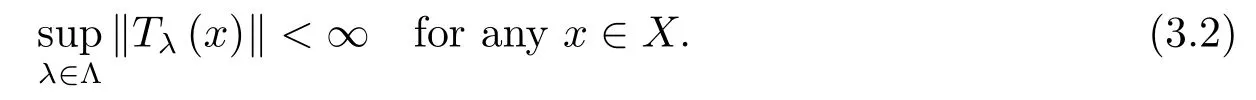
Now,de finep:X→R as follows
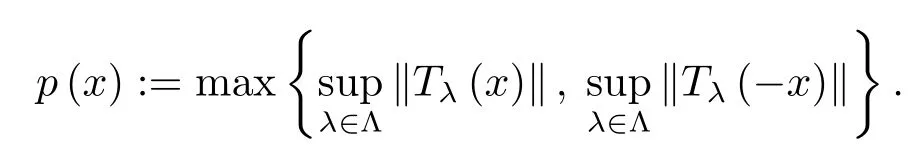
It is clear thatpis well-de fined(by(3.2))and is with nonnegativity,symmetry,absorbability and countable subadditivity.Hence,by Theorem 1.1,pis continuous onX,which implies
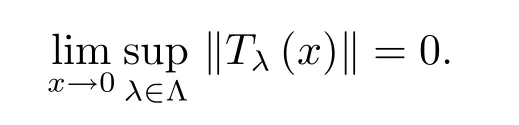
Corollary 3.2(The Generalized Closed Graph Theorem)LetXandYbeF-spaces.LetT:D(T)?X→Ybe a mapping which satisfies the following conditions
1)D(T)is a closed subspace ofX;
2)‖T(?x)‖=‖T(x)‖for everyx∈D(T);
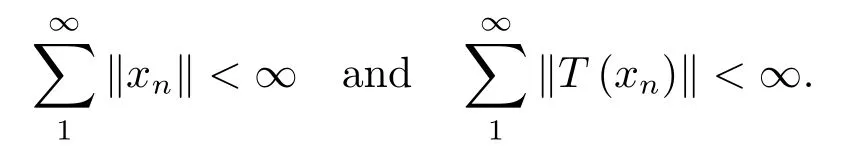
Then
(b)‖T(x)‖is continuous onD(T).
ProofDe finep:D(T)→R as followsp(x):=‖T(x)‖.It is not difficult to see thatpsatisfies all the conditions in Theorem 1.1.Hence,by Theorem 1.1,pis continuous onD(T),which implies(a)and(b).
Corollary 3.3(The Open Mapping Theorem)LetXandYbeF-spaces.LetT:D(T)?X→Ybe a closed linear operator withR(T)=Y.ThenTis an open mapping,i.e.,T(U)is open inYwheneverUis open inD(T).
ProofDe finep:Y→R as follows

Thenpis obviously with nonnegativity,symmetry,and absorbability onY.We now verify thatpis with countable subadditivity.Let a sequence{yn}ofYsatisfy<+∞.Then,by the completeness ofY,there exists a vectory∞ ∈Ysuch thatinY.We need to show that

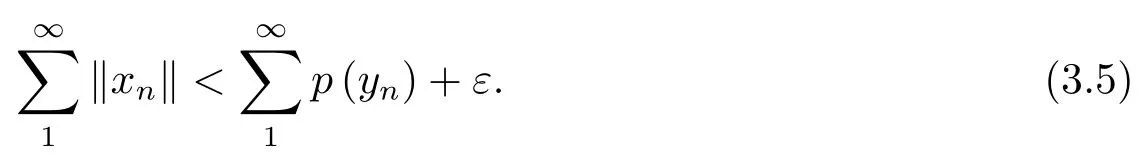
SinceXis anF-space,is convergent to a vectorx∞ofX.By the closedness ofT,we have thatx∞ ∈D(T)andTx∞=y∞.Hence,by(3.5),
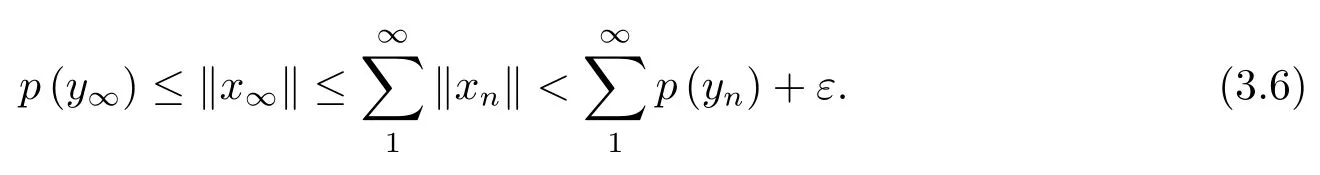
Note that theεis arbitrary,so(3.6)implies(3.4).Now,by Theorem 1.1,pis continuous onY.
To prove thatTis an open mapping,we have only to show that for everyε>0,there exists aδ>0 such that
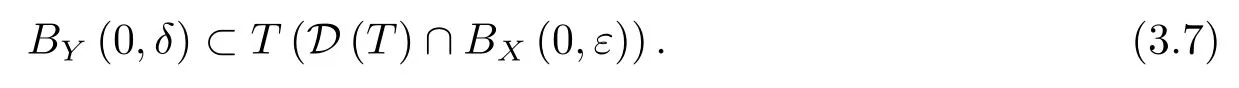
By the continuity ofp,for anyε>0,there is aδ>0 such that
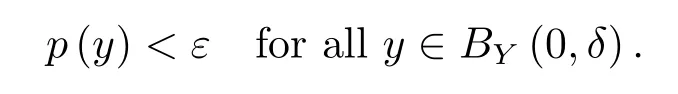
Hence,for everyy∈BY(0,δ),there exists a vectorx∈T?1(y)∩BX(0,ε)by the de finition ofp,and therefore(3.7)is true.
4 The Proof of Theorem 1.2
To prove Theorem 1.2,we prepare the following lemma.
Lemma 4.1LetYbe anF-space,{Yn}a sequence of closed subspaces ofY.Let Y be the set of all vectorsξ={yn}withyn∈Yn(for everyn∈N)and
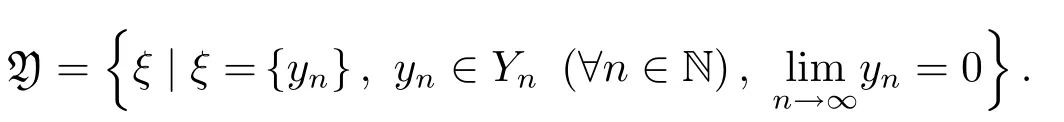
Then Y is anF-space by the algebrac operationsand the quasi-norm
ProofIt is easy to show that Y is a linear space and
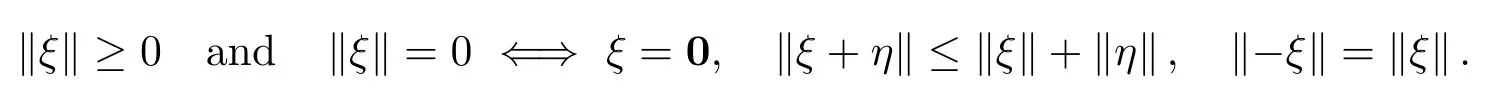
To prove that‖·‖is a quasi-norm on Y,we need only to show that

and

Noting thatξ={yn},as a subset ofY,is bounded and thatαk→0,we obtain(4.1).PutThenimpliesand therefore
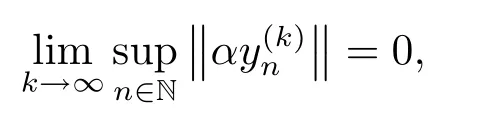
Next,we show that Y is complete.Letin Y.(k∈N).ThenHence there exists a sequenceofYsuch that

by the completeness ofY.Note that(4.3)implies thatPutthenξ(∞)∈Y andξ(k)→ ξ(∞)ask→ ∞in Y.
Proof of Theorem 1.2The proof will be carried out in three steps.
Step 1A)?B):Assume A)and put
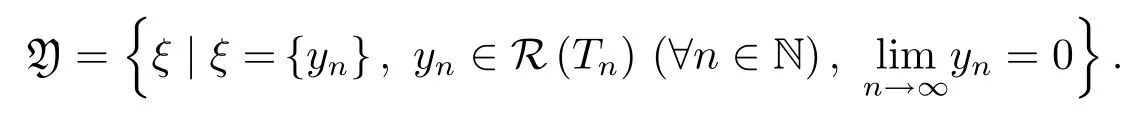
Then
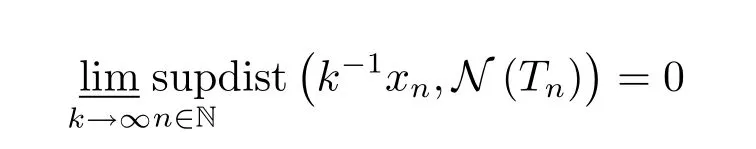
for anyξ={yn}∈Y and{xn}withxn∈T?1n(yn)(n∈N).Since
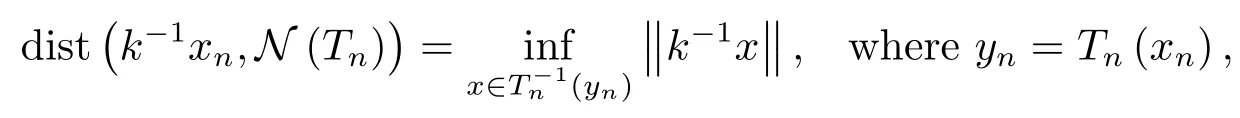
and since
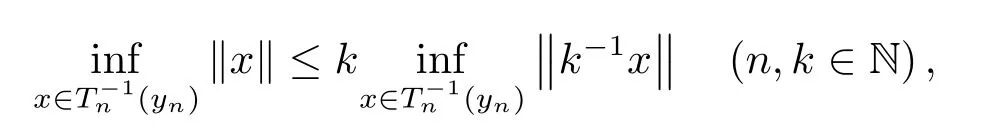
we have that
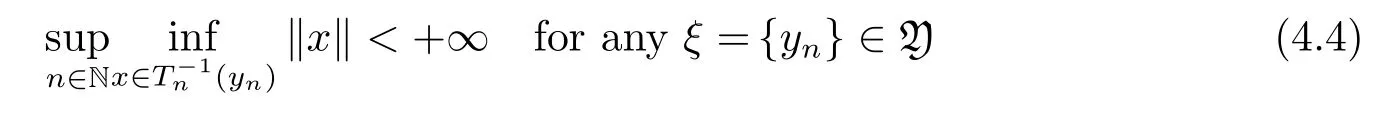
and that
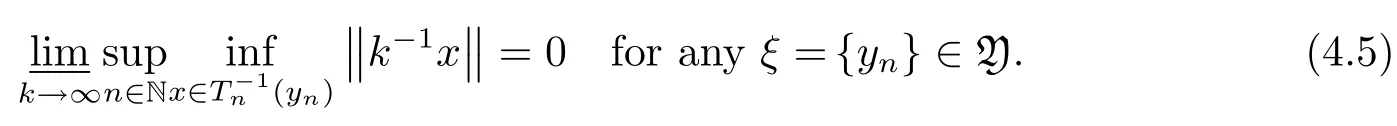
Noting thatR(Tn)(n∈N)are all closed,by Lemma 4.1,Y is anF-space by the algebrac operationsand the quasi-normDe finep:Y→R as follows
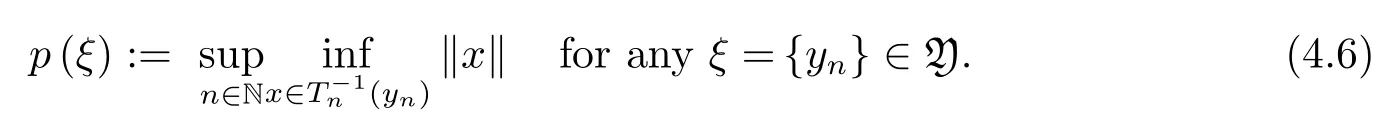
By(4.4),(4.6)and(4.5),pis well-de fined on Y,and is with nonnegativity,symmetry and absorbability.Next we verify thatpis with countable subadditivity.

We have to show that

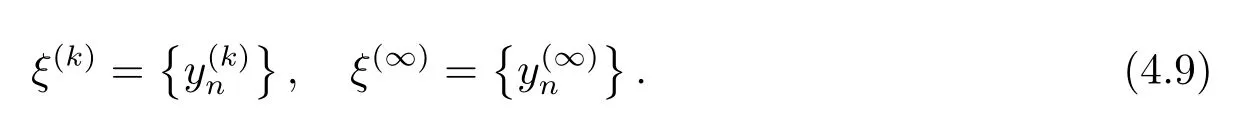
By the de finition ofp(see(4.6)),
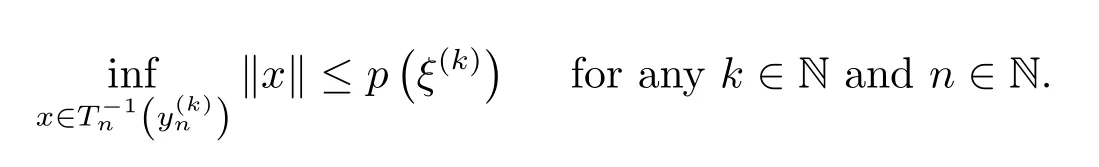
Therefore,for everyε>0,everyk∈N and everyn∈N,there exists a point∈such that
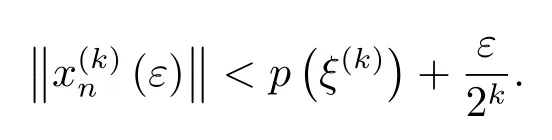
Hence,for everyε>0 and everyn∈N,there is a sequenceofD(Tn)such that
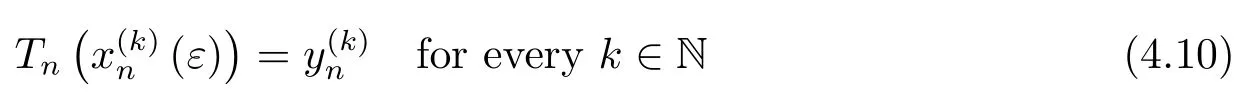
and
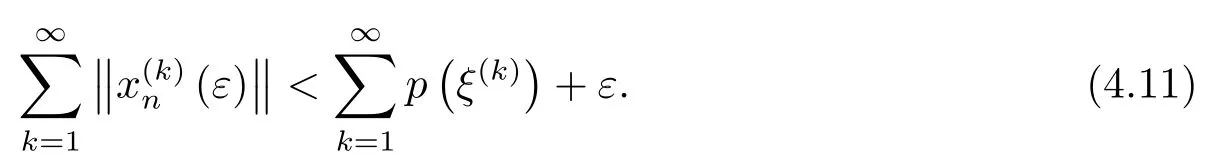
By(4.11)and the completeness ofX,there exists a point(ε)∈Xsuch that
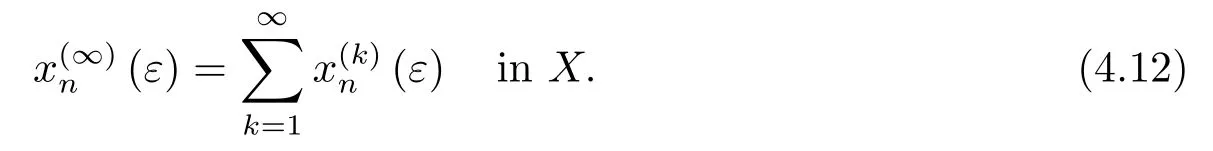
On the other hand,(4.10)with(4.7)and(4.9)implies that for everyn∈N,there holds
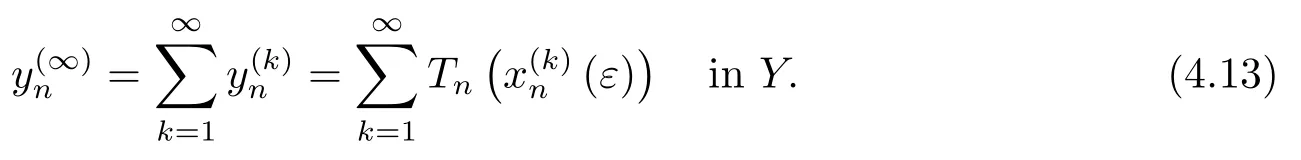
Since,for everyn∈N,Tnis closed,it follows from(4.12)and(4.13)that∈D(Tn)andHence,by(4.12)and(4.11),for everyε>0 and everyn∈N,we have that

So for everyε>0,we have
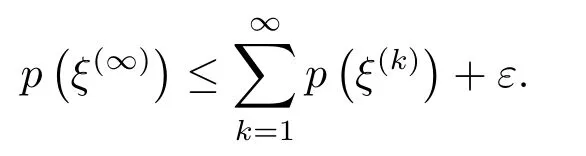
Thus(4.8)is true.
We have proved thatpsatisfies all the conditions of Theorem 1.1.Hence,pis continuous on Y,and is continuous at 0.This implies that for everyε>0,there exists aδ>0 such that
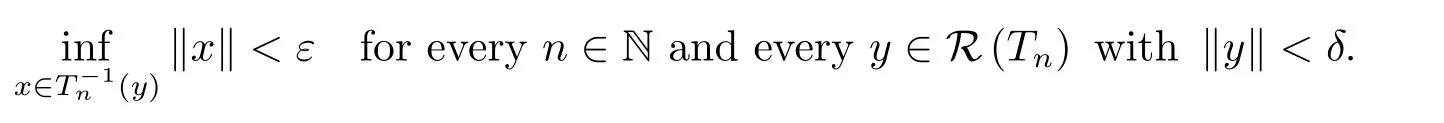
Therefore we obtain that for everyε>0 there exists aδ>0 such that
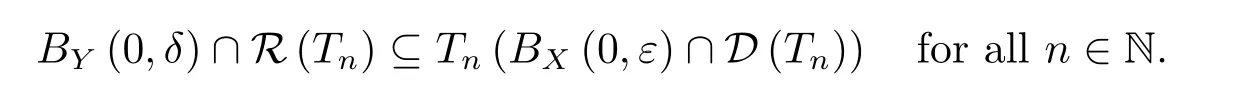
That shows that A)implies B).
Step 2B)?C)Assume that{Tn}satisfies B)and thatyn∈R(Tn)(n∈N)andWe have to show that
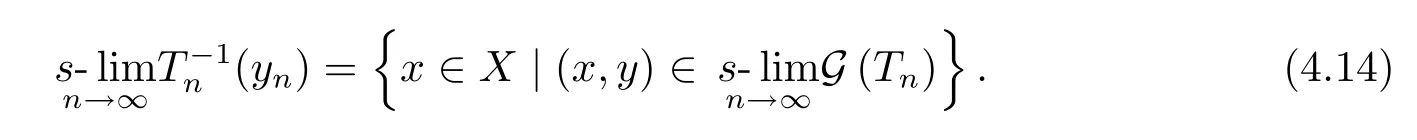
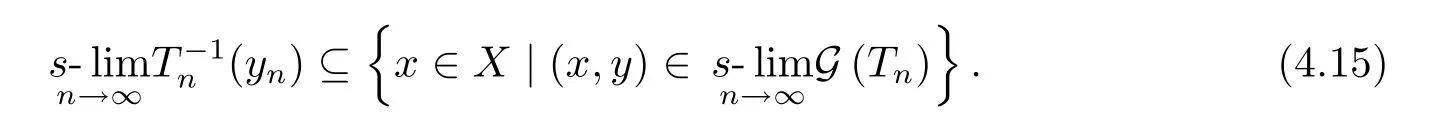
On the other hand,ifx∈Xsuch thatthen there exists a sequence{xn}ofXwithxn∈D(Tn)(n∈N)such thatand therefore
Since{Tn}satisfies B),i.e.,for everyε>0,there exists aδ>0 such that
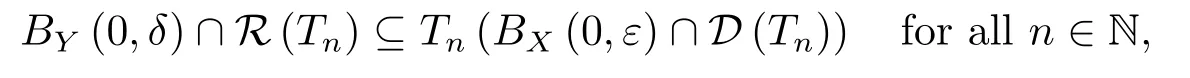
it follows from(4.16)that for everyε>0,there exists a natural numberNsuch that
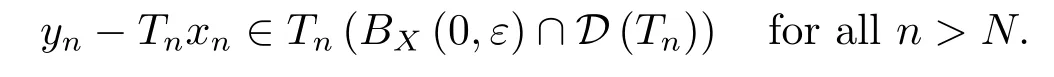
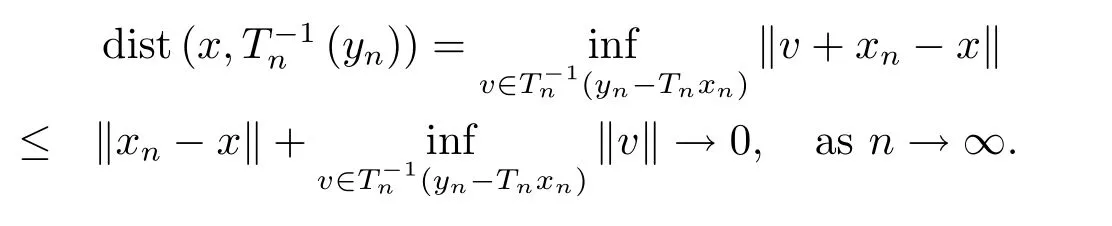

(4.14)follows from(4.15)and(4.17).
Step 3C)?A)Assume C)and let{xn}be a sequence ofXwithxn∈D(Tn)(n∈N)andThen
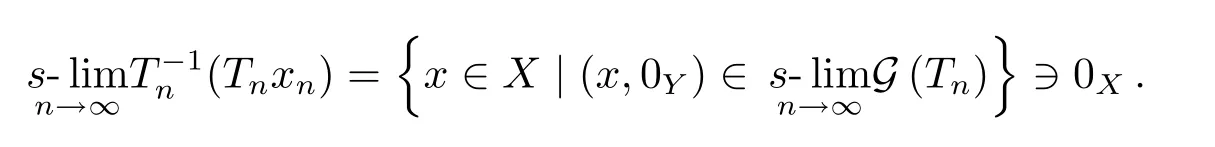
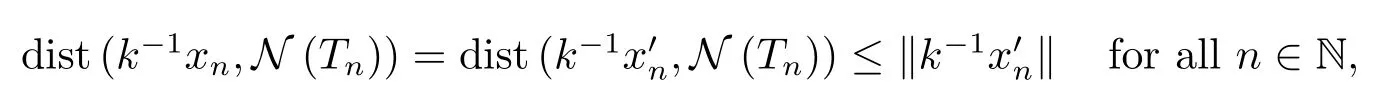
Remark 4.1In Theorem 1.2,ifXandYare Banach spaces,then the following three properties of{Tn}are equivalent:
A)For anyxn∈D(Tn)(n∈N)withthere holds
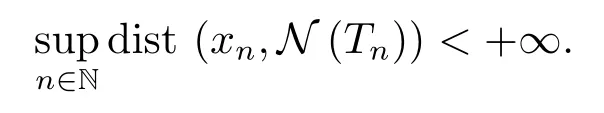
B)There exists aδ>0 such that
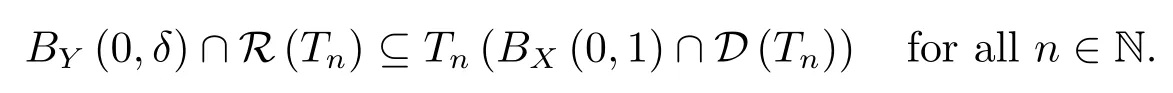
C)Ifyn∈R(Tn)(n∈N)with
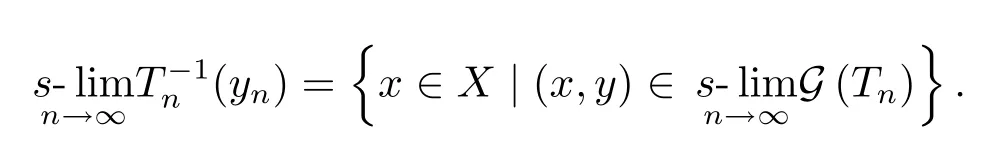
Remark 4.2The following case is of practical interest for the applications of Theorem 1.2:There exists a closed linear operatorT:D(T)?X→Ysuch that{Tn}is its consistent approximation scheme,that is,Here we provide two examples with the above case.
Example 4.1LetT,Tnbe all self-adjoint operators in a Hilbert spaceH,and let
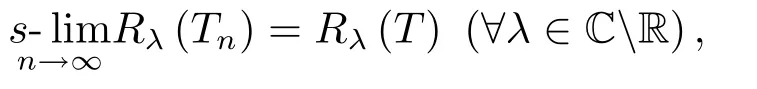
whereRλ(T)andRλ(Tn)denote the resolvent operator ofTandTn,respectively.Then{Tn}is a consistent approximation scheme ofT.See[6,pp.152–153]or[4,pp.148–149]for the proof of the statement.Now,by Theorem 1.2 we conclude that:ifR(Tn)(n∈N)are closed,and if

then for anyyn∈R(Tn)(n∈N)withthere holdsespecially,there holds
Example 4.2LetA,An∈B(X,Y),whereXandYbe Banach spaces,and letThen{An}is a consistent approximation scheme ofA.By Theorem 1.2,we conclude that:IfR(An)(n∈N)are closed,and if for anyxn∈D(An)(n∈N)withthere holdsthen the conclusion of Example 4.1 holds.
[1]Du N.The basic principles for stable approximations to orthogonal generalized inverses of linear operators in Hilbert spaces[J].Numer.Funct.Anal.Optim.,2005,26:675–708.
[2]Du N.Generalized Galerkin approximations for pseudo-inverses and operator equations of the first kind[J].Wuhan Univ.J.Nat.Sci.,2006,11:486–492.
[3]Lax P D,Richtmyer R.D.Survey of the stability of linear finite difference equations[J].Comm.Pure Appl.Math.,1956,9:267-293.
[4]Tong Y.S.A Course book of functional analysis(in Chinese)[M].Shanghai:Fudan Univ.Press,2003.
[5]Yosida K.Functional analysis(6th ed.)[M].Berlin:Springer-Verlag,1980.
[6]Zhang G Q,Guo M.Z.Lectures on functional analysis(in Chinese)[M].Beijing:Beijing Univ.Press,1990.
F-空間中的一個基本定理及其在數值分析中的應用
杜乃林,夏 煒
(武漢大學數學與統計學院,湖北武漢 430072)
本文針對F-空間中閉算子方程的一般逼近格式,研究其相容性、收斂性和穩定性之間的關系.所得的主要結果是:這種一般逼近格式在相容性條件下,其收斂性與穩定性是等價的.此定理可以看作是對Lax等價原理的推廣,是求解第一類閉算子方程的一般逼近格式的基本定理.為得到這一主要結果,本文還給出了F-空間中的一條基本定理,眾所周知的一致有界原理,閉圖像定理和開映像定理是其簡單推論.
F-空間;閉算子;收斂性;穩定性
O177.3;O177.92
46A04;65J05;65J22
A
0255-7797(2017)06-1177-12
date:2014-09-22Accepted date:2014-12-01
Biography:Du Nailin(1962–),male,born at Handan,Hebei,professor,major in ill-posed problems and generalized inverses.

