半次覆蓋遠離子群和有限群的可解性

李士恒,柳海萍,劉冬華

(1.鄭州航空工業管理學院理學院,河南鄭州 450015)

(2.鄭州航空工業管理學院經貿學院,河南鄭州 450015)

(3.鄭州鐵路職業技術學院公共教學部,河南鄭州 450052)

半次覆蓋遠離子群和有限群的可解性

李士恒1,柳海萍2,劉冬華3

(1.鄭州航空工業管理學院理學院,河南鄭州 450015)

(2.鄭州航空工業管理學院經貿學院,河南鄭州 450015)

(3.鄭州鐵路職業技術學院公共教學部,河南鄭州 450052)

本文定義了有限群的半次覆蓋遠離子群概念,研究了半次覆蓋遠離子群和有限群的可解性問題.利用某些半次覆蓋遠離子群刻劃了有限群的可解性,得到了若所有的sylow子群(或極大子群)半次覆蓋遠離則群可解,推廣了文獻[6]中的結果.

有限群;半次覆蓋遠離子群;極大子群;可解

1 引言

利用子群研究有限群的結構,在有限群的研究中有很重要的地位.很多學者都在這些方面進行了研究,得到了很多重要的結果.如著名的Huppert定理,即有限群為超可解當且僅當它的所有極大子群的指數為素數;有限群為冪零群當且僅當每個極大子群都正規;有限群可解當且僅當它的極大子群均c-正規(見文獻[1])等.很多學者對子群的正規性進行了推廣,并由此得到了許多關于可解性、超可解性和冪零性的一些充分條件.例如文獻[2]證明了如果群G的每一個Sylow子群有在G中正規的極大子群那么G超可解;文獻[3,4]中刻畫了滿足換位子條件的群的結構;文獻[10]用某些子群的半正規性刻畫了有限群的可解性等.郭秀云在文獻[5]中用覆蓋-離開子群刻畫了群的結構;樊惲、郭秀云[6]等介紹了概念半覆蓋遠離,這個概念是覆蓋遠離、幾乎正規(見文獻[6]定義2.1(2))的推廣,而幾乎正規是c-正規的推廣.他們用Sylow子群或極大子群的半覆蓋遠離性刻畫了有限群的可解性,也用其他一些子群的半覆蓋遠離性刻畫了有限群的超可解性.本文定義了有限群的半次覆蓋遠離性子群,用有限群的半次覆蓋遠離性子群刻劃群G的可解性.

文中,π是一個素數集合,G是一個群,所有的群都是有限群.π(G)表示群G的階的所有素因子作成的集合;如果數n的每一個素因子都在π中,稱n是一個π-數;H＜G表示H為G的真子群,H??G表示H為G的次正規子群,H為G的極大子群記作H＜·G;稱L為G的2-極大子群,如果存在G的極大子群M使L＜·M.

定義1.1設商群M/N為G的次正規因子,H是G的子群.若H滿足HM=HN(這里HM和HN不一定是群G的子群),則稱H覆蓋M/N;若H∩M=H∩N(?H∩M/H∩N=1),則稱H遠離M/N.如果H覆蓋或者遠離G的某個合成列的每個合成因子,那么稱H是G的半次覆蓋遠離子群.顯然這是半覆蓋遠離子群和次正規子群的一個推廣.

下面的例1.1說明半次覆蓋遠離子群既不是次正規子群也不是半覆蓋遠離子群,例1.2說明半次覆蓋遠離子群不一定覆蓋遠離每一個合成列,相關概念見文獻[7,A,第18節].

例1.1設G=3是N和S3的圈積(wreath product),其中S3為3次對稱群,N為一個非交換單群.再設H=D〈(12)〉,其中D為基群(base group)B的對角子群(diagonal subgroup),(12)為S3的一個置換.下面驗證H覆蓋遠離次正規列1＜N1＜N1×N2＜B＜B〈(123)〉＜G,其中N1={(a,1,1)|a∈N},N2={(1,a,1)|a∈N}.顯然有N1∩H=1=N1∩1、N1∩H=1=(N1×N2)∩H、(N1×N2)H=B〈(12)〉=BH、B∩H=D=B〈(123)〉∩H、(B〈(123))〉H=G(由|B〈(123)〉H|=得)成立,因此H覆蓋遠離上述次正規列.

另一方面,由B∩H=D≠1和BH=B〈(12)〉≠H得H不覆蓋或遠離G的主因子B/1,又B是G唯一的極小正規子群,所以H不覆蓋或遠離G的任何主列,即是H不是G的半覆蓋遠離子群.顯然H也不是G的次正規子群(否則H∩B=D是G的次正規子群從而也是B的次正規子群,但由文獻[8,第一章,9.12]可看出這是不可能的).

例1.2設G=A5×〈(67)〉,其中A5為5次交錯群,(67)為S7的一個置換,H=〈(12)(34)(67)〉.則H覆蓋遠離合成列1＜A5＜G(也是主列),但不覆蓋遠離G的合成列1＜ 〈(67)〉＜G(也是主列).

2 引理

引理2.1設H是群G的子群,1＜···＜N＜M＜···＜G是G的一個次正規列.如果H覆蓋（遠離）M/N,那么H覆蓋(遠離)這個次正規列細化后的在M和N之間的任一個合成因子.

證設A/B是滿足N≤B＜A≤M的群G的合成因子.當H覆蓋M/N時,由HM?HA?HB?HN得H覆蓋A/B.如果H遠離M/N,那么H∩M=H∩N.因為H∩M≥H∩A≥H∩B≥H∩N,所以H∩A=H∩B.引理得證.

引理2.2設H≤G,NG且(|H|,|N|)=1.如果MG,那么M∩HN=(M∩H)(M∩N).

證設W=M∩HN.由M??G得存在次正規子群Gi(i=0,1,···,r)滿足M=Gr?Gr?1?···?G0=G.對r用數學歸納法.

當r=1時MG.從而WHN,WH=HW且NW=WN.又由(|H|,|N|)=1得(|HN:N|,|HN:H|)=1.因此由文獻[7,A,1.6(c)]得W=(W∩H)(W∩N)=(M∩H)(M∩N).

假定Gr?1∩HN=(Gr?1∩H)(Gr?1∩N).設Hr?1=(Gr?1∩H),Nr?1=(Gr?1∩N).由M≤Gr?1和歸納假定得W=M∩(Gr?1∩HN)=M∩Hr?1Nr?1=W∩Hr?1Nr?1.

由MGr?1得M⊥Hr?1和M⊥Nr?1,顯然也有(|Hr?1Nr?1:Hr?1|,|Hr?1Nr?1:Nr?1|)=1.再次由文獻[7,A,1.6(c)]得

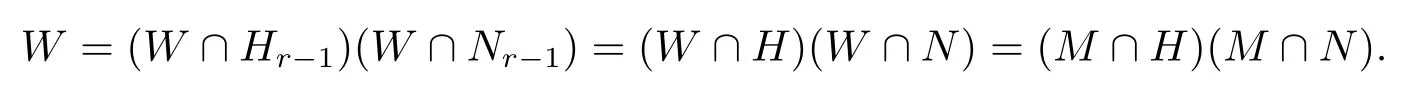
引理2.3設H是G的半次覆蓋遠離子群.

(a)如果H≤M≤G,那么H是M的半次覆蓋遠離子群.

(b)如果N≤H或(|H|,|N|)=1,那么HN/N是G/N的半次覆蓋遠離子群.

證 (a)設H是G的半次覆蓋遠離子群.那么G有合成列1=Gn?Gn?1?···?G0=G使對i=1,···,n有HGi=HGi?1或H∩Gi?1=H∩Gi.設Mi=Gi∩M,i=0,···,n.那么有HMi=HMi?1或H∩Mi=H∩Mi?1.于是H覆蓋遠離M的次正規列1=MnMn?1···M0=M,從而由引理2.1得H是M的半次覆蓋遠離子群.

(b)設H是G的半次覆蓋遠離子群,H覆蓋遠離主列1=G0＜G1＜···＜Gt=G.即有HGi=HGi?1或H∩Gi=H∩Gi?1.HGi=HGi?1顯然結論成立,只需要證明H∩Gi=H∩Gi?1時的情形.

如果N≤H,那么H/N∩Gi?1N/N=N(H∩Gi?1)/N(由文獻[7,A,1.3]可得)且H/N∩GiN/N=N(H∩Gi)/N.結合H∩Gi=H∩Gi?1得(H/N∩GiN/N)=(H/N∩Gi?1N/N).于是,由引理2.1得H/N是G/N的半次覆蓋遠離子群.

如果(|H|,|N|)=1,那么HN/N∩Gi?1N/N=N(HN∩Gi?1)/N.又由引理2.2得HN∩Gi?1=(H∩Gi?1)(N∩Gi?1),所以HN/N∩Gi?1N/N=N(H∩Gi?1)(N∩Gi?1)/N=N(H∩Gi?1)/N≌H∩Gi?1.同理有H/N∩GiN/N≌H∩Gi.因此HN/N∩Gi?1N/N=HN/N∩GiN/N,從而H/N是G/N的半次覆蓋遠離子群.

引理2.4設G為有限群且L是G的2-極大子群.如果L=1,那么G可解.

證如果L=1,那么G有一個素數階的極大子群,從而由文獻[8,第四章,7.4]得G可解.

引理2.5設G為有限群,A/B為G的次正規因子,H≤G,則有

(1)(A∩H)B=A?HB=HA;

(2)(A∩H)B=B?B∩H=A∩H.

證(1)若(A∩H)B=A則HB=(H(A∩H))B=H((A∩H)B)H=HA;反之,若HB=HA則由文獻[7,A,1.3]得A=A∩HA=A∩HB=(A∩H)B.

(2)若(A∩H)B=B則由文獻[7,A,1.3]得B∩H=((A∩H)B)∩H=(A∩H)(B∩H)=A∩H;反之,若B∩H=A∩H則B(A∩H)=B(B∩H)=B.

3 主要結果

定理3.1設G是有限群.如果G的每一個極大子群都是G的半次覆蓋遠離子群,那么G是可解的.

證假設結論不成立,設G是極小階反例.

因為G的商群的極大子群的逆像是G的極大子群,由引理2.3,G的商群滿足定理的假設.因此,對任意的NG,由G是極小階反例得G/N是可解的.如果G有兩個極小正規子群,那么由可解群類是飽和群系得G是可解的.因此,假定G有唯一的極小正規子群,設為N.若N是可解的則G是可解的,所以假定N非可解.于是N=N1×N2×···×Nr,其中N1≌N2≌···≌Nr為非可解單群.由文獻[7,A,15.2]得CG(N)=1.

設P=P1×P2×···×Pr＞1,其中Pi∈Sylp(Ni),i=1,2,···,r,則P∈Sylp(N).由Frattini推斷得G=NNG(P).因為N是G的極小正規子群且P＜N,所以存在M＜·G使NG(P)≤M,從而G=MN.由題設,可設M覆蓋遠離合成列1=G0＜G1＜···＜Gt=G.由文獻[7,A,14.3]得N≤NG(G1),若N∩G1=1,則有1=CG(N)≥G1,這是不可能的.因此N∩G1≠1,又N∩G1??G,結合G1為極小次正規子群得N≥G1.由文獻[8,第一章,9.12定理]可假設N1=G1.因為M∩G1≥P1＞1,所以M覆蓋G1/1,即有MG1=M,從而N1=G1≤M.由N1N得所以由N是唯一的極小正規子群得所以G=MN=M,與M＜·G矛盾.定理得證.

定理3.2若群G的每一個2-極大子群都是G的半次覆蓋遠離子群,那么G是可解的.

證對每一個M＜·G,由定理的假設條件和引理2.3得M的每一個極大子群均在M中半覆蓋遠離.因此由定理3.1得M可解.

另一方面,對每一個N?G,由引理2.3,有G/N滿足定理的假設條件.如果N≠1,那么對|G|用歸納法得G/N可解.因此,如果N＜G那么N必含于某一個極大子群,從而N可解,G可解.因此,可假定G是非交換單群.于是,對G的任一個2-極大子群L,由假設條件得L=G或L=1.由L是一個2-極大子群知L=G不可能,于是必有L=1,從而由引理2.4得G是可解群.

定理3.3群G是可解群當且僅當G的任意子群都是G的半次覆蓋遠離子群.

證必要性:群G是可解群,設1=Gn?Gn?1?···?G0=G是G的合成列,則由G是可解群得Gi?1/Gi為p階群,i=1,···,n?1.設H≤G,則Gi?1∩HGi或Gi?1∩H?Gi.若前者成立,則(Gi?1∩H)Gi=Gi?1;若后者成立,則(Gi?1∩H)Gi=Gi.由引理2.5分別得

充分性由定理3.1或定理3.2顯然可得.

注3.1由定理3.3知道半次覆蓋遠離子群只能刻畫群的可解性,且定理3.1和定理3.2的條件都是群可解的充要條件.

定理3.4群G是p-可解群當且僅當G有Sylowp-子群P是G的半次覆蓋遠離子群.

證必要性:假設群G是p-可解群,1=Gn?Gn?1?···?G0=G是G的合成列,則由G是p-可解群得Gi?1/Gi為p階群或p′-群,i=1,···,n?1.設P是G的任一Sylowp-子群.則Gi?1/Gi為p階群時,Gi?1∩PGi;Gi?1/Gi為p′-群時,Gi?1∩P?Gi.從而Gi(Gi?1∩P)=Gi?1和Gi(Gi?1∩P)=Gi.由引理2.5分別得PGi=PGi?1和Gi∩P=Gi?1∩P.

充分性:假設G有Sylowp-子群P是G的半次覆蓋遠離子群,則可設P覆蓋遠離G的一個合成列1=Gn?Gn?1?···?G0=G.

若PGi=PGi?1,則由引理2.5得(Gi?1∩P)Gi=Gi?1.由Gi?1??G得Gi?1∩P∈Sylp(Gi?1).從而Gi?1/Gi為p-群,結合Gi?1/Gi為單群得Gi?1/Gi為p階群.

若Gi∩P=Gi?1∩P,則由引理2.5得Gi(Gi?1∩P)=Gi.由Gi?1??G得Gi?1∩P∈Sylp(Gi?1).因此Gi?1/Gi為p′-群.

由定理3.4可得推論3.1.

推論3.1群G是可解群當且僅當G的任意Sylow子群都是G的半次覆蓋遠離子群.

由推論3.1、定理3.1和定理3.3得推論3.2.

推論3.2(見文獻[6,定理2.2])設G是一個群.則如下的3個命題等價:

(l)G是一個可解群;

(2)G的每一Sylow子群在G中具有半覆蓋遠離性;

(3)G的每一極大子群在G中都具有半覆蓋遠離性.

平行于文獻[6,定理3.1],結合定理3.3,只可能得到如下結論.

定理3.5群G是可解群當且僅當G每一個非循環Sylow子群的任一個極大子群都是G的半次覆蓋遠離子群.

證必要性由定理3.3顯然可得,下面證明充分性.

(1)設P是G的一個Sylowp-子群,1=Gn?Gn?1?···?G0=G是G的任一合成列,其中p∈π(G).則

于是(Gi?1∩P)Gi/Gi是Gi?1/Gi的Sylowp-子群.且由

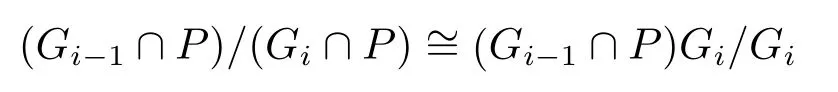
得(Gi?1∩P)Gi/Gi同構于P的一個截斷.

(2)設P是G的一個Sylowp-子群,若P循環則由(1)得Gi?1/Gi的Sylowp-子群為循環群.

(3)設P是G的一個Sylowp-子群,P1＜·P.若P非循環,則P1覆蓋遠離G的某一合成列1=Gn?Gn?1?···?G0=G.

(i)若P1覆蓋Gi?1/Gi,則由引理2.5得Gi?1=(P1∩Gi?1)Gi.于是

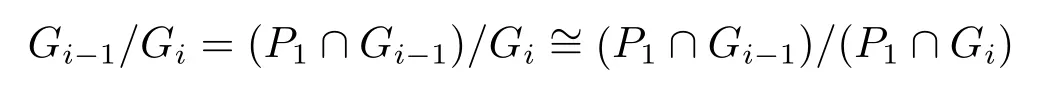
是一個p-群,結合Gi?1/Gi是單群得Gi?1/Gi為p階群.

(ii)若P1遠離Gi?1/Gi,則由引理2.5得Gi=(P1∩Gi?1)Gi.

若(P∩Gi?1)?P1,則(P∩Gi?1)=(P1∩Gi?1).因此得Gi=(P∩Gi?1)Gi,從而由P∩Gi?1為Gi?1的Sylowp-子群得Gi?1/Gi為p′-群.

若(P∩Gi?1)P1則(P∩Gi?1)P1=P.又由P1＜·P得P1?P且|P:P1|=p.于是由|(P∩Gi?1)||P1|/|(P1∩Gi?1)|=|P|得|(P∩Gi?1):(P1∩Gi?1)|=p.所以

為p階群或1.

總之,由(2),(3)得Gi?1/Gi的Sylow子群為循環群.因此Gi?1/Gi可解(見文獻[9,V,6.2定理]),從而為素數階群.所以群G是可解群.

[1]Wang Y.C-normality of groups and its properties[J].J.Alg.,1996,180(3):954–965.

[2]Sirnivasan S.Two sufficient conditions for supersolvability of finite groups[J].Isreal J.Math.,1980,35(3):210–214.

[3]Beidleman J C,Robinson D J S.On finite groups satisfying the Permutizer condition[J].J.Alg.,1997,191(2):686–703.

[4]Zhang J.A note on finite groups satisfying permutizer condition[J].Kexue Tongbao,1986,31(6):363–365.

[5]Guo X,Shum K P.Cover-avoidance properties and the structure of finite groups[J].J.Pure Appl.Alg.,2003,181(2-3):297–308.

[6]樊惲,郭秀云,岑嘉評.關于子群的兩種廣義正規性的注記[J].數學年刊,2006,27A(2):169–176.

[7]Doerk K,Hawkes T.Finite soluble groups[M].New York:Walter de Gruyter Berlin,1992.

[8]胡貝特B著,黃建華,李慧陵譯.有限群論(第一卷)[M].福州:福建人民出版社,1992.

[9]徐明曜.有限群導引(上)[M].北京:科學出版社,1987.

[10]韋華全,班桂寧.某些冪零子群與可解性[J].數學雜志,1999,19(3):257–262.

SEMI-SUBNORMAL-COVER-AVOIDANCE SUBGROUPS AND THE SOLVABLITY OF FINITE GROUPS

LI Shi-heng1,LIU Hai-ping2,LIU Dong-hua3
(1.School of Science,Zhengzhou University of Aeronautics,Zhengzhou 450015,China)
(2.School of Economics and Trade,Zhengzhou University of Aeronautics,Zhengzhou 450015,China)
(3.Department of Public Education,Zhengzhou Railway Vocational and Technical College,Zhengzhou 450052,China)

In this paper,we de fine semi-subnormal-cover-avoidance subgroups of finite groups and study the solvability between groups and their semi-subnormal-cover-avoidance subgroups.With semi-subnormal-cover-avoidance subgroups,we characterize the solvability of finite groups and obtain the results that the group is soluble if all of its sylow groups(or maximal subgroups)are semi-subnormal-cover-avoidance subgroups,which generalize the results in[6].

finite group;Semi-subnormal-cover-avoidance subgroups;maximal subgroups;solvable

20D10;20D35

O152.1

A

0255-7797(2017)06-1303-06

2016-01-28接收日期:2016-06-08

國家自然科學基金青年項目資助 (11501176);河南省高等學校重點科研項目資助(16A110039).

李士恒(1977–),男,河南鄧州,講師,主要研究方向:群論.