BELL POLYNOMIALS AND ITS SOME IDENTITIES
GUO Jing,LI Xiao-xue
(1.School of Mathematics and Computer Science,Jiangxi Science&Technology Normal University,Nanchang 330038,China)
(2.School of Mathematics,Northwest University,Xi’an 710127,China)
BELL POLYNOMIALS AND ITS SOME IDENTITIES
GUO Jing1,LI Xiao-xue2
(1.School of Mathematics and Computer Science,Jiangxi Science&Technology Normal University,Nanchang 330038,China)
(2.School of Mathematics,Northwest University,Xi’an 710127,China)
In this paper,we introduce a new polynomial called Bell polynomials.By using the elementary and combinational methods,we prove some identities for this polynomials.As an application of these identities,we give an interesting congruence for Bell numbers.
Bell numbers;Bell polynomials;identity;combinational method
1 Introduction
For any integersn≥k≥0,letS(n,k)denote the number of partitions of a set withnelements intoknonempty blocks.It is clear thatS(n,k)>0 for all 1≤k≤n,andS(n,k)=0 for 1≤n<k.PutS(0,0)=1 andS(0,k)=0 fork≥1,S(n,0)=0 forn≥1.These numbers were introduced by Stirling in his book“Methodus Di ff erentialis”(see[3–5]).Now they are called as the Stirling numbers of the second kind.These numbers satisfy the recurrence relation
The number of all partitions of a set withnelements is

called also a Bell number(or exponential number),related contents can be found in many papers or books.For example,see[6–8].
These numbers satisfy the recurrence formula

whereB(0)=1 by de finition.
The generating function ofB(n)is given by

where exp(y)=ey.
The numbersB(n)can be represented also as the sum of a convergent series(Dobinski’s formula)

see Pólya and Szeg?[9]for these basic properties.
In this paper,we introduce a new polynomialsB(x,n)(called Bell polynomials)as follows

It is clear thatB(0,x)=1,B(1,x)=x,B(2,x)=x+x2,B(3,x)=x+3x2+x3,···.Ifx=1,thenB(n,1)=B(n),the well known Bell numbers.About the properties ofB(n,x),it seems that none had studied it yet,at least we have not seen any related papers before.The problem is interesting,because it can help us to further understand the properties of Bell numbers.
The main purpose of this paper is using the elementary and combinational methods to study the computational problem of the sums

Theorem 1Letkbe a positive integer withk≥1.Then for any positive integern≥1,we have the identity

where the polynomialsB(n,x)satisfy the recurrence formulaB(0,x)=1,B(1,x)=x,B(2,x)=x+x2,B(3,x)=x+3x2+x3,and

For the polynomialsB(n,x),we also have a similar Dobinski’s formula.
Theorem 2For any positive integern≥1,we have the identities
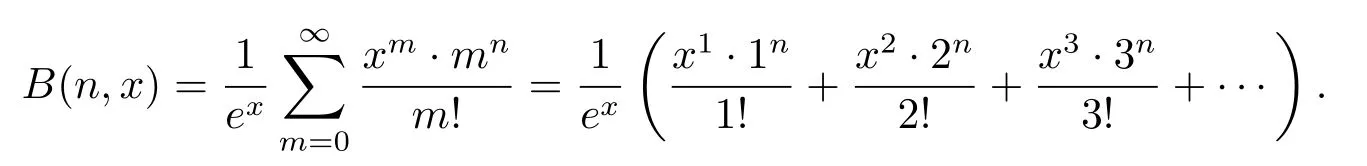
From Theorem 1 and the recurrence formula ofB(n,x),we may immediately deduce the following congruence.
Corollary 1Letpbe an odd prime.Then for any positive integerk≥1 with(k,p)=1,we have the congruence

Corollary 2For any positive integern,we have the identity

2 Proof of the Theorems
In this section,we shall complete the proofs of our theorems.First we give a sample lemma,which are necessary in the proof of our theorems.Hereinafter,we shall use some elementary number theory contents and properties of power series,all of these can be found in references[1]and[2],so they will not be repeated here.
LemmaFor any real numberx,let functionf(t)=exp(x(et?1)),then we havef(n)(0)=B(n,x)for all integersn≥0,wheref(n)(t)denotes thenthderivative off(t)for variablet.
ProofWe prove this lemma by complete induction.It is clear thatf(0)=1=B(0,x),f′(t)=xet·exp(x(et?1))=xet·f(t),andf′(0)=x=B(1,x).So the lemma is true forn=0,1.Assume thatf(n)(0)=B(n,x)for all 0≤n≤r.Then note thatf′(t)=xet·f(t),so from the properties of derivative(Newton-Leibnitz formula),we have

Applying(2.1)and inductive hypothesis,we have

That is,f(r+1)(0)=B(r+1,x).
Now the lemma follows from the complete induction.
Proof of Theorem 1For any positive integerk≥2,it is clear thatfk(t)=exp(kx(et?1)),then from(1.4),we have

On the other hand,letg(t)=fk(t)=exp(kx(et?1)),then from the de finition of the power series and lemma,we also have

Combining(2.2)and(2.3)we may immediately deduce the identity

This proves Theorem 1.
Proof of Theorem 2Applying the power serieswe have

Comparing the coefficients oftnin(1.4)and(2.4),we may immediately deduce the identity

This proves Theorem 2.
Proof of Corollary 1Letpbe an odd prime,taken=p+1 in Theorem 1,then from the properties ofB(n,x)and Theorem 1,we have

or


Note thatk≥2 anda1+a2+···+ak=p+1,so if there are three ofa1,a2,···,akare positive integers,then

If there are only two ofa1,a2,···,akare positive integers,and both of them are greater than one,then we also have

If there are only two ofa1,a2,···,akare positive integers,and one isp,another is 1,then we also have

If only one ofa1,a2,···,akare positive integers,then it must bep+1.This time we have

Combining(2.5)–(2.10)and note that identity

we have

or

This proves the first congruence of Corollary 1.The second congruence follows from the second identity of Corollary 2 withn=p.
Proof of Corollary 2Letf(t,x)=exp(x(et?1)),then from(1.4),we have

On the other hand,from the de finition off(t,x),we also have

Comparing the coefficients oftnin(2.11)and(2.12),we may immediately deduce the identity

Note that the recurrence formulafrom(2.13)we may immediately deduce the identityThis completes the proofs of our all results.
[1]Tom M Apostol.Introduction to analytic number theory[M].New York:Springer-Verlag,1976.
[2]Tom M Apostol.Mathematical analysis(2nd ed.)[M].Boston:Addison-Wesley Publishing Co.,1974.
[3]Stirling J.Methodus differentialis[M].Londini:Sive Tractatus de Summation et Interpolazione Serierum In finitarum,1730.
[4]Boole G.Calculus of finite differences[M].London:Chelsea Publishing Company,1860.
[5]Caralambides C A.On weighted Stirling and other related numbers and come combinatorial applications[J].Fibonacci Quar.,1984,22:296–309.
[6]Conway H J,Guy R K.The book of numbers[M].New York:Copernicus,1996.
[7]Corcino C B.An asymptotic for ther-Bell numbers[J].Matimyás Mat.,2001,24:9–18.
[8]Tan M H,Xiang Y H,Zha Z W.Someinifite summation identities of the second kind[J].J.Math.,2013,33(3):388–392.
[9]Pólya G,Szeg? G.Problems and theorems in analysis I[M].New York:Springer-Verlag,1972.
關于Bell多項式及其它的一些恒等式
過 靜1,李小雪2
(1.江西科技師范大學數學與計算機科學學院,江西南昌 330038)
(2.西北大學數學學院,陜西西安 710127)
本文引入了一個新的多項式,即Bell多項式.利用初等數論及組合方法,證明了包含該多項式的一些恒等式.作為這些恒等式的應用,給出了關于Bell數的同余式.
Bell數;Bell多項式;恒等式;組合方法
O157.1
11B37;11B83
A
0255-7797(2017)06-1201-06
date:2015-04-14Accepted date:2015-07-06
Supported by National Natural Science Foundation of China(11371291);Jiangxi Science and Technology Normal University(xjzd2015002).
Biography:Guo Jing(1973–),female,born at Jinxian,Jiangxi,associate professor,major in mathematics.

