電液伺服系統神經網絡辨識及控制器設計

韓桂華++王鵬飛++張此軍

摘要：針對閥控缸電液位置伺服系統非線性建模問題，采用神經網絡進行系統模型辨識。采用LM遺傳算法對三層BP神經網絡的權值和閾值進行修正，通過訓練系統的輸入/輸出數據建立非線性系統辨識模型。基于此模型，設計模糊PI控制器，利用智能權函數在線自動調整和修改模糊控制器的規則。利用xPC技術建立閥控缸伺服實驗臺，以實驗臺階躍輸出信號作為改進BP神經網絡辨識信號，以實驗臺正弦輸出信號作為驗證信號。實驗表明：該神經網絡辨識模型的可信性得以驗證；通過對比智能權函數模糊PI控制器和模糊控制器的實驗曲線，表明前者控制效果更好。

關鍵詞：

改進BP神經網絡；系統辨識；智能權函數；模糊控制；電液位置伺服系統；遺傳算法

DOI：1015938/jjhust201705004

中圖分類號： TP183，TP273

文獻標志碼： A

文章編號： 1007-2683（2017）05-0018-06

Neural Network Identification and Controller on Electrohydraulic Servo System

HAN Guihua，WANG Pengfei，ZHANG Cijun

（School of Mechanical and Power Engineering， Harbin University of Science and Technology ， Harbin 150080， China）

Abstract：The neural networks system identification was used in nonlinear model on valvecontrolcylinder electrohydraulic position servo system The three layers BP neural network weights and threshold were optimized using LM genetic algorithm， the relationship of system input and output was analyzed and neural network identification model was presented A kind of fuzzy PI controller was designed based on the model， which can automatically adjust and modify the rules of fuzzy controller by using the intelligent weight function A real time electrohydraulic servo test bench was built with the xPC technique The test bench step output was used to identify in the improved BP neural network and the sinusoidal output was used to verify in experiment Experiment results show that the credibility is verified on neural network identification model； and that the control effect of the intelligent weight function fuzzy PI controller is better than the fuzzy controller

Keywords：improved BP neural network； system identification； intelligent weight function； fuzzy control； electrohydraulic position servo system； genetic algorithm

收稿日期： 2016-02-13

基金項目： 國家自然科學基金青年科學基金（51405113）；國家國際科技合作專項資助合作項目（2012DFR70840）

作者簡介：

韓桂華（1972—），女，博士，教授，Email：641544105@qqcom；

王鵬飛（1990—），男，碩士研究生；

張此軍（1990—），男，碩士研究生

0引言

建立系統的數學模型是控制理論的基礎，電液伺服系統因系統的死區特性、增益以及自激振蕩等是一個模型參數和結構不確定的非線性系統[1-3]，因此，在工程應用中獲得一個與實際系統完全等價的數學模型，并以此為基礎進行控制器的仿真設計是非常困難的。神經網絡廣泛應用于眾多領域，但在非線性系統模型辨識中還存在收斂速度慢，學習時間長等問題。本文通過分析標準BP算法現狀與存在的問題[4-6]，將BP神經網絡結構與遺傳算法相結合，建立閥控缸電液位置伺服系統的辨識模型。

模糊控制根據經驗制定模糊規則即可對被控制對象實施控制，特別適用于被控制對象是非線性時變的不確定系統。但常規模糊控制器的修正因子α一經確定，其模糊控制規則便不可改變。帶有智能權函數的模糊控制器就可以通過智能權函數來在線自調整修正因子α，以達到在線自調整模糊控制規則的目的，從而使模糊控制器能夠適應被控制對象的變化[7-9]。模糊控制器由于缺少積分環節，控制過程中還存在穩態誤差難以消除的問題。本文以閥控缸電液伺服系統神經網絡辨識模型為對象，設計一種智能權函數模糊PI控制器，用于改善和消除系統的穩態誤差，實現模糊規則在線自調整，并借助于xPC實時系統的半實物仿真環境和MATLAB軟件[10]，驗證神經網絡辨識模型及模糊控制器的有效性。endprint

1xPC半實物仿真實驗環境

利用xPC技術建立的電液伺服實驗臺的半實物仿真環境如圖1所示，在xPC Target環境中，宿主機為裝有MATLAB/simulink軟件的pc機，目標機為研華工控機，兩者通過以太網LAN實現通訊，用于控制器實時測試和系統半實物仿真等。

實驗臺的動力機構為典型的對稱閥控制對稱液壓缸模型如圖2所示，計算機給伺服閥提供控制信號Ur，經過數據輸出（D/A）卡、伺服放大器，控制液壓缸。為了實現位置閉環控制，由位移傳感器把位置信號Us反饋給數據采集（A/D）卡，偏差值ΔU先后經控制器處理和伺服放大器放大，然后以電流信號傳遞給電液伺服閥，從而控制伺服閥的開口大小，達到通過控制伺服閥的流量變化來控制液壓缸位移的目的，同時在示波器和顯示屏上顯示出液壓缸的實時位置。

2基于改進BP神經網絡的系統辨識

21LM算法原理

BP神經網絡（back propagation neural network）的 BP算法通過信號正向傳播和誤差反向傳播確定權值。在正向傳播過程中，輸入的信息經由隱含層計算傳向輸出層。如果輸出層得到的信息與期望的輸出有誤差，誤差信號沿原來的神經網絡通路反向傳播來修正每層神經元的權值與閾值，使網絡的誤差平方和不斷減小。這個過程循環執行，直到輸出層的輸出達到了期望值，或達到設定學習次數而終止。

標準的BP算法收斂速度慢，學習速率不易確定，很難用于工程實際中。為了優化BP網絡，目前常用的優化算法包括變速率算法、共軛梯度算法、高斯-牛頓算法、LM算法等[11-14]。與其他算法比較， LM算法既具有高斯-牛頓法的局部收斂性，又具有梯度下降法法的全局特性，有效改善網絡的收斂性能。

當實際輸出與期望輸出不符時，產生誤差用E表示。

E=12∑iK=1e2k（w）（1）

式中： w為網絡權值和閾值所組成的向量；

ek（w）為誤差。

若wk表示第k次迭代的權值和閾值所組成的向量，wk+1表示第k+1次迭代的權值和閾值所組成的向量。wk+1與wk之間的關系表示為wk+1=wk+Δw。其中權值增量Δw表示為：

Δw=[JT（w）J（w）+μI]-1JT（w）e（w）（2）

式中：I為單位矩陣；μ為用戶定義的學習率；J（w）為雅克比矩陣，即

J（w）=

e1（w）w1e1（w）w2…e1（w）wn

e2（w）w1e2（w）w2…e2（w）wn

eN（w）w1eN（w）w2…eN（w）wn（3）

LM算法是為了在以近似二階訓練速率進行修正時避免計算Hessian矩陣而設計的。此雅可比矩陣可以通過標準的前饋網絡得到，所以LM算法比梯度法快得多。從式（2）中可知，若μ=0，則為高斯-牛頓法；若μ值很大，則LM算法接近梯度下降法。每次迭代完之后，若減小學習率μ，當期望輸出接近實際輸出的時候，逐漸與高斯-牛頓法相似。這樣就提高了學習速率。

22基于改進BP神經網絡實驗臺的模型建立

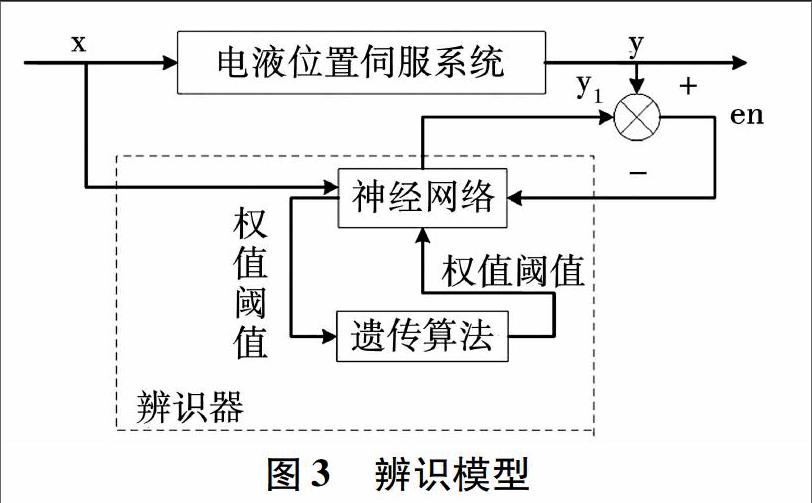
神經網絡應用于系統辨識不需要預先選擇實際系統的模型，而是直接通過訓練系統的輸入/輸出數據進行辨識。由于神經網絡具有非線性的特點，可以不受非線性模型的限制。本文采用典型的三層BP神經網絡，再利用遺傳算法對神經網絡的權值和閾值進行修正，使要求的誤差準則函數達到最小，從而優化BP神經網絡，最終建立辨識模型，如圖3所示。

對位置反饋閉環控制來進行（電液位置伺服系統）辨識。考慮到非線性系統的時變性和干擾性，進行多組實驗。分別以正弦信號和階躍信號為輸入，記錄其輸出數據。這樣在xPC實時系統的半實物仿真環境下，在線得到輸入輸出數據。其中，階躍信號所得的數據用于改進BP神經網絡系統辨識，正弦信號進行驗證。

在MATLAB環境下輸入nntool，進入神經網絡工具箱辨識GUI。將訓練樣本數據導入GUI，建立神經網絡。采用單輸入單輸出電液伺服系統，確定了改進 BP網絡的輸入節點數L=10，輸出節點數N=1。對于隱含層節點數的選取，經過反復的訓練，當M=17時誤差最小且精度最高。各層傳遞函數類型：隱含層選用單極性S型函數，輸出層選用線性傳遞函數purelin，學習算法采用LM算法（trainlm）。采用均方誤差（MSE）性能函數網絡的誤差函數進行修正。創建神經網絡如圖4所示。

23辨識結果驗證

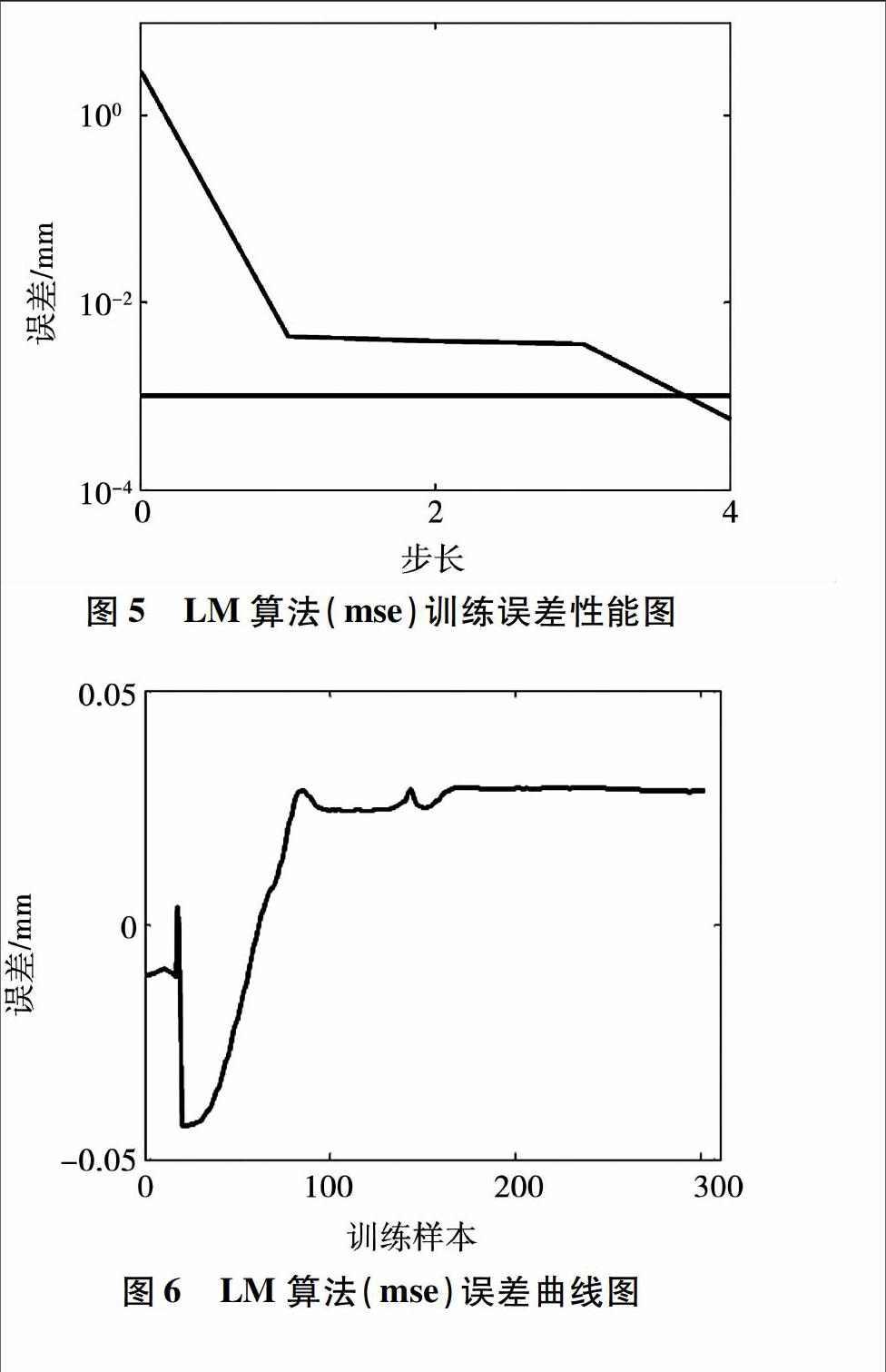
根據建立的神經網絡進行辨識，以階躍信號為輸入，LM算法（MSE）性能曲線如圖5～圖7所示。

將訓練誤差參數值設為0001，其余均為默認值。得到的訓練誤差曲線在第四步就達到了所設目標值。訓練輸出誤差曲線比較平滑，說明誤差小。

從圖7中可以得知，辨識輸出與實際輸出之間的相關系數都達到了09以上。

根據建立的辨識模型，可對此非線性系統的任何輸入進行辨識輸出。為下一步針對本系統的控制理論研究提供了前提和保障。

3智能權函數模糊PI控制器

31帶修正因子的模糊控制器

模糊控制器常用的是二維模糊控制器，其模糊規則查詢表、量化因子Ke和Kc以及比例因子Ku，一旦確定之后，在控制過程中就不能夠再改變。因此，需考慮在不同的誤差E和誤差變化EC等級時，引入不同大小的修正因子，實現模糊控制規則自調整。在誤差E較大時，控制的主要任務是消除誤差，這時對控制規則中誤差E的加權度就應該變大些；而當誤差E較小時，此時系統已接近穩態，控制的主要任務就變成了盡快地使系統達到穩定，為了有效地減小超調，就要在控制規則中對誤差變化EC的加權度大些，以使誤差變化EC所起的作用變大。常用方法有[15]。引入多個調整因子、使用自調整因子和使用自調整函數的方法。本文所使用的智能權函數法是自調整函數法的一種。endprint

由帶修正因子α的模糊控制器的自調整原理可知，可利用誤差和誤差變化的絕對值作為各自的加權，為滿足對二者加權之和等于1的條件，誤差及誤差變化的自調整權函數可分別設計為

αe=|E|/（|E|+|EC|）（4）

αec=|EC|/（|E|+|EC|）（5）

式中E和EC分別為誤差和誤差變化的模糊值，顯然誤差的權函數αe和誤差變化的權函數αec滿足αe+αec=1的條件。

根據式（4）和式（5）所確定的權函數，可以得到智能權函數模糊控制規則的解析表達式為：

U=-<αe×E+αec×EC>（6）

智能權函數模糊控制算法是一種仿人智能控制策略，特點是權函數僅是輸入變量的函數，其控制系統可以自動地根據輸入變量實時地調整權函數，從而實現在線調整模糊控制規則。為改善控制器的控制性能，消除穩態誤差，引入PI控制結構，如圖8所示。

32智能權函數模糊PI控制器的設計

在MATLAB中利用模糊推理系統 （FIS） 編輯器，構造一個雙輸入（偏差E和偏差變化EC）、單輸出（控制量U）的二維模糊控制系統。采用Mamdani型推理方法，其中模糊邏輯的and算法采用“prod”，or算法采用“probor”，清晰化算法采用“centroid”，蘊含算法采用“prod”，綜合算法采用“max”。

模糊輸入變量（E和EC）和輸出變量（U）的隸屬度函數均采用高斯型隸屬度函數。論域及語言值分別如下[16-20]：

偏差E的論域及語言值為：

{負，零，正}={n，z，p}={6，5，4，3，2，1，0，1，2，3，4，5，6}

偏差變化EC的論域及語言值為：

{負，零，正}={n，z，p}={06，05，……，01，0，01，……，05，06}

控制量U的論域及語言值為：

{負大，負中，負小，負，零，正，正小，正中，正大}={nb，nm，ns，n，z，p，ps，pm，pb}={6，5，4，3，2，1，0，1，2，3，4，5，6}。

輸入變量和輸出變量的模糊子集隸屬度函數如表1所示。

電液位置伺服系統主要是通過控制電液伺服閥的閥門開口大小和速度來達到控制液壓缸活塞的位移的目的，根據知識和經驗歸納可總結出9條模糊控制規則。模糊控制規則如表2所示。結合智能權函數的原理，在MATLAB/Simulink環境下建立智能權函數模糊PI控制系統的仿真圖，如圖9所示。

33實驗分析

為了驗證基于神經網絡辨識模型所設計的智能權函數模糊PI控制器在實際應用中的有效性，在xPC半實物仿真實驗臺上進行了實時控制實驗研究。

實驗時將智能權函數模糊PI控制器與常規模糊控制器進行比較研究，其階躍響應和正弦響應的實驗結果曲線分別如圖11和圖12所示，圖中曲線1為輸入，曲線2為模糊控制輸出，曲線3為智能權函數模糊PI控制器輸出。由圖可見，模糊控制器和智能權函數模糊PI控制器的穩態性能和跟蹤性能都表現得不錯。但是模糊控制由于沒有引入積分項，階躍響應曲線有余差存在，而智能權函數模糊PI控制器幾乎沒有余差，并且階躍響應的上升時間更快、超調量更小，正弦響應時其跟蹤響應時間更短。

4結論

本文以電液伺服實驗臺為例，通過xPC半實物仿真采樣獲得被控對象的輸入輸出數據，將BP神經網絡結構與遺傳算法相結合，建立了基于LM算法的神經網絡辨識模型。實驗表明通過在神經網絡外部擬合系統的輸出，對本質非線性電液位置伺服系統進行辨識，調節網絡內部的權值獲得的神經網絡辨識模型可信性好。以此模型為對象，結合智能權函數的作用原理，利用MATLAB/Simulink設計了一種智能權函數模糊PI控制器。這種控制器能夠通過在線自調整修正因子α來在線自調整模糊控制規則，改善了常規模糊器不能很好地適應控制對象的變化的缺點。與常規模糊控制器相比，智能權函數模糊PI控制器的控制精度更好。

參 考 文 獻：

[1]GIOVANNELLI F，GIREMUS A Bayesian Noise Model Selection and System Identification Based on Approximation of the Evidence[M].Statistical Signal Processing （SSP）， 2014 IEEE Workshop on， 2014：125-128

[2]LING T G， RAHMAT M F， HUSAIN A R Anfis Modeling of ElectroHydraulic Actuator System[C]// Signal Processing and its Applications （CSPA）， 2012 IEEE 8th International Colloquium on 2012：89 – 92

[3]LING T G， RAHMAT M F， HUSAIN A R System Identification and Control of an ElectroHydraulic Actuator System[C]// Signal Processing and its Applications （CSPA）， 2012 IEEE 8th International Colloquium on IEEE， 2012：85-88

[4]謝蓄芬， 劉泊， 王德軍 一種改進BP神經網絡在模式識別中的應用[J]. 哈爾濱理工大學學報， 2004（5）：63-65

[5]YU F， XU X A Shortterm Load Forecasting Model of Natural Gas Based on Optimized Genetic Algorithm and Improved BP Neural Network[J]. Applied Energy， 2014， 134（134）：102-113endprint

[6]LIU Y Y， SHEN D R， CHEN Y J Multiinnovation Stochastic Gradient Identification Algorithm Based on Feedforward Neural Networks [J]. Journal of Harbin University of Commerce： Natural Sciences Edition， 2006，22（2）： 83-86

[7]李勁松，金志揚 基于修正因子智能權函數的汽車ABS模糊控制算法仿真研究[J]. 汽車科技，2010（3）：55-57

[8]IZADIKHAH M Deriving Fuzzy Weights of Criteria from Inconsistent Fuzzy Comparison Matrices by Using Goal Programming Method [J].Journal of Intelligent & Fuzzy Systems Applications in Engineering & Technology， 2013， 25（1）：69-80

[9]黃強， 張曉， 張勝強 油壓跟隨性的智能權函數模糊控制研究[J]. 九江學院學報， 2009， 28（3）：6-8

[10]張立勛， 董玉紅， 王懷軍 基于半物理仿真技術的機電伺服系統模型辨識研究[J]. 機電一體化， 2006， 12（2）： 30-32

[11]JIANG B， WANG B Parameter Estimation of Nonlinear System Based on Genetic Algorithms [J]. Control Theory & Applications， 2000， 17（1）：150-152

[12]張本國， 李強，王葛 基于改進BP神經網絡的連鑄漏鋼預報[J]. 中國機械工程，2012（2）：204-207

[13]尹光志，李銘輝，李文璞 基于改進BP神經網絡的煤體瓦斯滲透率預測模型[J]. 煤炭學報，2013（7）：1179-1184

[14]高雪鵬， 叢爽 BP網絡改進算法的性能對比的研究[J]. 控制與決策，2011， 16 （2）： 167-171

[15]WANG Chihsu， HUNG Kunneng Dynamic System Identification Using Highorder Hopfield Based Neural Network [J]. Asian journal of control 2012， 14（6）： 1553-1566

[16]溫嘉斌， 麻宸偉 無刷直流電機模糊PI控制系統設計[J]. 電機與控制學報， 2016， 20（3）：102-108

[17]于艦，孫桂濤，高炳微 液壓四足機器人驅動器 CAN 總線通信[J].哈爾濱理工大學學報，2013，18（2）：78-80

[18]XU Baochuang， ZHANG Yingying An Improved Gravitational Search Algorithm for Dynamic Neural Network Identification [J]. International Journal of Automation and computing， 2014， 11（4）：434-440

[19]榮盤祥， 董文波， 于林 混沌自調整模糊PID控制器的研究與應用[J]. 哈爾濱理工大學學報， 2014， 19（2）：26-30

[20]雷賓賓， 保宏， 許謙 區間二型模糊 PI/PD 控制器設計與結構分析[J]. 電機與控制學報， 2016， 20（6）：50-63

（編輯：關毅）endprint