基于PIM法車(chē)橋耦合模型Duhamel項(xiàng)迭代格式選擇

桂水榮， 萬(wàn) 水， 陳水生

(1.東南大學(xué)交通學(xué)院 南京, 210096) (2.華東交通大學(xué)土木建筑學(xué)院 南昌,330013)

10.16450/j.cnki.issn.1004-6801.2017.05.007

基于PIM法車(chē)橋耦合模型Duhamel項(xiàng)迭代格式選擇

桂水榮1,2， 萬(wàn) 水1， 陳水生3

(1.東南大學(xué)交通學(xué)院 南京, 210096) (2.華東交通大學(xué)土木建筑學(xué)院 南昌,330013)

考慮荷載在積分步長(zhǎng)內(nèi)的協(xié)調(diào)分解和不變常量，結(jié)合模態(tài)綜合疊加技術(shù)，建立移動(dòng)彈簧質(zhì)量車(chē)橋耦合振動(dòng)模型，引入精細(xì)積分算法(precise intergration method,簡(jiǎn)稱(chēng)PIM)，并采用科茨及高斯積分格式展開(kāi)精細(xì)積分中Duhamel非齊次項(xiàng)進(jìn)行求解。以移動(dòng)彈簧質(zhì)量車(chē)模型作用于簡(jiǎn)支梁橋?yàn)槔治龇e分步內(nèi)荷載等效方法及Duhamel非齊次項(xiàng)展開(kāi)方式對(duì)車(chē)橋耦合振動(dòng)響應(yīng)的影響。研究結(jié)果表明：荷載協(xié)調(diào)分解并結(jié)合科茨積分格式計(jì)算結(jié)果與解析解更接近，Newmark-β法積分步長(zhǎng)內(nèi)荷載分解形式對(duì)計(jì)算結(jié)果影響較小；荷載協(xié)調(diào)分解的高斯積分格式計(jì)算結(jié)果呈發(fā)散趨勢(shì)，待定系數(shù)法計(jì)算結(jié)果與實(shí)際偏離較大；Newmark-β法能滿足工程需要，但在保證相同計(jì)算精度時(shí)，需采用較小積分步長(zhǎng)、同時(shí)耗費(fèi)較多計(jì)算時(shí)間；與其他幾種數(shù)值方法相比，積分步長(zhǎng)內(nèi)荷載協(xié)調(diào)分解并將科茨積分格式引入精細(xì)積分的算法(PIM-Cotes-Harmonize,簡(jiǎn)稱(chēng)PIM-C-H法)，具有快速收斂且計(jì)算快的優(yōu)勢(shì)。

車(chē)橋耦合振動(dòng)模型； 精細(xì)積分法； Duhamel項(xiàng)； 迭代格式選擇

引 言

公路橋梁與汽車(chē)荷載之間的相互作用，近些年一直是國(guó)內(nèi)外學(xué)者研究橋梁?jiǎn)栴}的一個(gè)熱點(diǎn)。數(shù)值模擬車(chē)橋耦合振動(dòng)響應(yīng)，運(yùn)用模態(tài)綜合疊加技術(shù)并結(jié)合隱式Newmark-β算法求解，一直是國(guó)內(nèi)外學(xué)者廣泛采用的方法[1]，分析中需通過(guò)保證積分步長(zhǎng)來(lái)確保計(jì)算結(jié)果的收斂性[2]。鐘萬(wàn)勰[3]提出的精細(xì)積分法，能給出齊次結(jié)構(gòu)動(dòng)力響應(yīng)的高精度解答。對(duì)于非齊次結(jié)構(gòu)動(dòng)力方程引起的Duhamel非齊次項(xiàng)求解，因非齊次項(xiàng)的求解方式直接影響了非齊次動(dòng)力方程計(jì)算精度，國(guó)內(nèi)許多學(xué)者對(duì)此展開(kāi)研究。譚述君等[4]利用Duhamel積分矩陣，導(dǎo)出非線性方程求解一般格式，結(jié)合Adams線性多步法，構(gòu)造基于精細(xì)積分方法的算法。高強(qiáng)等[5]利用大規(guī)模動(dòng)力系統(tǒng)矩陣的稀疏性和動(dòng)力問(wèn)題的物理特性，提出一種改進(jìn)的快速精細(xì)積分方法。張文志等[6]將初值問(wèn)題轉(zhuǎn)化為邊值問(wèn)題，利用快速傅里葉變換(fast Fourier trans formation,簡(jiǎn)稱(chēng)FFT)進(jìn)行求解。汪夢(mèng)甫等[7]將高斯積分方法與精細(xì)積分法中的指數(shù)矩陣相結(jié)合，求解非齊次方程的特解，計(jì)算時(shí)不需對(duì)矩陣求逆。富明慧等[8]提出了一種廣義精細(xì)積分方法，對(duì)非齊次項(xiàng)為多項(xiàng)式和指數(shù)函數(shù)，能實(shí)現(xiàn)特解的精細(xì)積分，但對(duì)任意形式荷載并不適用。同時(shí)，儲(chǔ)德文等[9]對(duì)比幾種數(shù)值算法指出，非齊次方程的特解求解需根據(jù)荷載的性質(zhì)選擇合適的積分方法。

根據(jù)非齊次方程的荷載形式，黃濤等[10]提出了一種求解非線性動(dòng)力學(xué)方程的預(yù)測(cè)-校正數(shù)值算法。結(jié)合車(chē)橋耦合振動(dòng)特點(diǎn)，杜憲亭等[11]構(gòu)造了一種改進(jìn)的高斯精細(xì)積分算法用于求解結(jié)構(gòu)非線性問(wèn)題。運(yùn)用精細(xì)積分法求解非線性方程，引入指數(shù)矩陣后，加大積分步長(zhǎng)并不影響齊次方程計(jì)算精度，但對(duì)于行駛在公路橋梁上的汽車(chē)荷載，積分步長(zhǎng)內(nèi)荷載作用位置不斷發(fā)生變化，荷載項(xiàng)為時(shí)間、系統(tǒng)運(yùn)動(dòng)的非線性隱性函數(shù)。積分步長(zhǎng)內(nèi)荷載的等效方法及非齊次項(xiàng)的積分格式，對(duì)計(jì)算結(jié)果將有怎樣的影響，需進(jìn)一步研究。

根據(jù)車(chē)橋耦合振動(dòng)特點(diǎn)，結(jié)合模態(tài)綜合疊加技術(shù)，筆者建立移動(dòng)彈簧質(zhì)量車(chē)橋耦合振動(dòng)模型，考慮節(jié)點(diǎn)荷載在積分步長(zhǎng)內(nèi)協(xié)調(diào)分解和不變常量?jī)煞N格式，運(yùn)用精細(xì)積分算法并結(jié)合科茨及高斯積分格式進(jìn)行求解，研究移動(dòng)彈簧質(zhì)量車(chē)模型作用下非齊次項(xiàng)迭代格式對(duì)車(chē)橋耦合振動(dòng)響應(yīng)的影響。

1 車(chē)橋耦合精細(xì)積分模型

1.1 車(chē)橋耦合振動(dòng)模型

將車(chē)輛模型簡(jiǎn)化為由兩個(gè)質(zhì)量體系組成的移動(dòng)彈簧質(zhì)量車(chē)模型。假定車(chē)輛與橋梁始終保持接觸，車(chē)輛模型的質(zhì)量由車(chē)輪質(zhì)量m2及車(chē)體的簧載質(zhì)量m1組成，車(chē)輪和懸架系統(tǒng)的彈簧剛度及阻尼分別等效為剛度k1、阻尼c1的彈簧-阻尼系統(tǒng)。假設(shè)簡(jiǎn)支梁橋靜止時(shí)為平衡位置，車(chē)輛以速度v行駛，梁的動(dòng)撓度為y(x,t)，簧載質(zhì)量m1的動(dòng)位移為z(t)，車(chē)輪m2始終與梁體保持接觸不脫離，且位移與所在位置的橋梁撓度y(x,t)一致，移動(dòng)彈簧質(zhì)量車(chē)模型如圖1所示。

圖1 移動(dòng)彈簧質(zhì)量車(chē)橋耦合振動(dòng)模型Fig.1 A beam subjected to a moving spring mass system

根據(jù)達(dá)朗貝爾原理，移動(dòng)彈簧質(zhì)量車(chē)輛模型振動(dòng)方程為

(1)

車(chē)輛振動(dòng)過(guò)程中，作用于橋梁的力為

(2)

運(yùn)用有限元方法，將橋梁離散成歐拉梁?jiǎn)卧瑯蛄赫駝?dòng)方程可以表示為

(3)

其中:Mb,Cb,Kb分別為橋梁系統(tǒng)的質(zhì)量、阻尼和剛度矩陣；u為橋梁?jiǎn)卧?jié)點(diǎn)向量；Fb為作用于橋梁上的外荷載。

采用Rayleigh阻尼計(jì)算橋梁結(jié)構(gòu)阻尼Cb=αMb+βKb，其中α和β為Rayleigh阻尼系數(shù)。橋梁節(jié)點(diǎn)模態(tài)空間取r階，根據(jù)模態(tài)振型的正交性，不考慮各階模態(tài)的相干性，經(jīng)振型正交分解， 式(3)可以改寫(xiě)為

(4)

(5)

其中：Mbv，Cbv，Kbv為車(chē)橋耦合振動(dòng)廣義剛度、阻尼及質(zhì)量矩陣；ybv為車(chē)橋耦合振動(dòng)方程坐標(biāo)向量；ybv=[q1,q2,…,qr,z]T；Fbv為車(chē)橋耦合振動(dòng)廣義荷載向量。

(6)

其中：N為單元插值函數(shù)；Q，S，A1，A2，B1，B2分別為車(chē)橋耦合振動(dòng)引起的阻尼及剛度矩陣修正系數(shù)矩陣；MV，CV，KV分別為車(chē)輛模型質(zhì)量、阻尼、剛度矩陣。

1.2 移動(dòng)荷載節(jié)點(diǎn)等效分解

1.2.1 積分步長(zhǎng)內(nèi)荷載協(xié)調(diào)分解

如圖2所示，假設(shè)簡(jiǎn)支梁第i單元長(zhǎng)度為li，移動(dòng)彈簧質(zhì)量荷載在i單元內(nèi)，自i端向j端以速度v勻速行駛。某一積分步長(zhǎng)Δt內(nèi)，在τ時(shí)刻彈簧質(zhì)量系統(tǒng)由A點(diǎn)移動(dòng)到B點(diǎn)，此時(shí)A，B兩點(diǎn)均在i單元內(nèi)。數(shù)值迭代時(shí)，任意tk時(shí)刻作用于A點(diǎn)，而tk+1時(shí)刻移動(dòng)至B點(diǎn)，A點(diǎn)和B點(diǎn)分別距i單元起點(diǎn)的距離為x1和x2。假設(shè)t時(shí)刻，移動(dòng)彈簧質(zhì)量車(chē)模型距i單元起點(diǎn)距離為x，有

x=vtk-xk，ξ=x/l=ξ1t-ξ2

(7)

圖2 移動(dòng)彈簧質(zhì)量車(chē)模型在i單元內(nèi)移動(dòng)Fig.2 A moving spring mass system moving in the i-th element

圖3 i單元內(nèi)，荷載節(jié)點(diǎn)等效分解Fig.3 A moving spring mass system moving in the i-th element

(8)

其中:Ni(ξ)(i=1～4)為梁?jiǎn)卧牟逯岛瘮?shù)。

此時(shí)作用于橋梁上的外荷載等效到單元節(jié)點(diǎn)荷載可以表示成

(9)

將式(7),(8)代入(9)，并整理可得

Fv=(r0+r1t+r2t2+r3t3)[-ΦT(m1+m2)g]

(10)

其中:ri(i=0～3)為外荷載的常系數(shù)向量。

1.2.2 積分步長(zhǎng)內(nèi)荷載為常量

如圖2所示，假設(shè)積分步長(zhǎng)內(nèi)荷載為常量，此時(shí)單元內(nèi)荷載等效到節(jié)點(diǎn)荷載，積分步長(zhǎng)內(nèi)等效節(jié)點(diǎn)荷載為不變常量，任意tk時(shí)刻，節(jié)點(diǎn)i和節(jié)點(diǎn)j的等效節(jié)點(diǎn)荷載相等，式(8)改寫(xiě)為

(11)

此時(shí)，式(11)在積分步長(zhǎng)內(nèi)，荷載為定值，求解算法與Newmark-β法求解車(chē)橋耦合振動(dòng)算法相同[12]。

1.3 精細(xì)積分算法分析

車(chē)橋耦合振動(dòng)模型的二階非齊次微分方程，運(yùn)用精細(xì)積分法求解其通解，并對(duì)Duhamel非齊次項(xiàng)采用數(shù)值迭代積分格式分析。

將式(5)轉(zhuǎn)化成狀態(tài)空間方程

(12)

(13)

式(12)的解可以寫(xiě)成如下形式

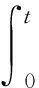
(14)

將計(jì)算時(shí)間間隔Δt劃分成若干步，則可以得到t+Δt時(shí)刻與t時(shí)刻系統(tǒng)響應(yīng)之間關(guān)系

(15)

其中:exp為指數(shù)矩陣，第1項(xiàng)為通解，采用精細(xì)積分算法求解；第2項(xiàng)為非奇次方程的特解，Duhamel非齊次項(xiàng)運(yùn)用科茨積分法及高斯積分法，分別進(jìn)行數(shù)值迭代求解。

2 PIM法Duhamel項(xiàng)迭代格式分析

2.1 科茨積分格式

式(15)Duhamel非齊次項(xiàng)的解，可以采用科茨積分格式進(jìn)行求解。對(duì)式(15)進(jìn)行離散，令τ=tk+1-tk，τ為積分步長(zhǎng)，則

(16)

2.2 高斯積分法

采用高斯積分公式展開(kāi)式(15)中Duhamel項(xiàng)[11]，得

vt+Δt=exp(HΔt)+Δt/2×

(17)

其中：m為高斯積分點(diǎn)個(gè)數(shù)；θi,wi分別為高斯積分點(diǎn)位置、權(quán)重系數(shù)。

隨著m增大積分精度提高，計(jì)算量隨之增大。結(jié)合有限元等參元高斯積分的計(jì)算經(jīng)驗(yàn)[11]，取m=3。式(17)中參數(shù)按如下參數(shù)取值

w1=5/9；w2=8/9；w3=5/9

(18)

式(17)離散后的非線性荷載項(xiàng)涉及t+θiΔt時(shí)刻的系統(tǒng)運(yùn)動(dòng)狀態(tài)，可以通過(guò)以下方法確定。假定t到t+Δt之間任一時(shí)刻τ的位移，可由t,t+Δt時(shí)間步的位移、速度依據(jù)三次Hermite函數(shù)插值唯一確定

(19)

其中:N1(θ)=1-3θ2+2θ3；N2(θ)=3θ2-2θ3；N3(θ)=θ-2θ2+θ3；N4(θ)=θ3-θ2；θ=(τ-t)/Δt；0≤θ≤1。

(20)

3 算例分析

例1為研究PIM數(shù)值積分法計(jì)算車(chē)橋耦合振動(dòng)響應(yīng)的有效性及積分步長(zhǎng)內(nèi)荷載分解方法對(duì)車(chē)橋耦合振動(dòng)響應(yīng)的影響，如圖4所示，以某一簡(jiǎn)支梁橋受移動(dòng)常量力為例，對(duì)比分析幾種常用數(shù)值算法、PIM數(shù)值算法與解析解的誤差。圖中：m為單位長(zhǎng)度質(zhì)量；EI為簡(jiǎn)支梁橋抗彎剛度。

圖4 移動(dòng)常量力作用于簡(jiǎn)支梁橋示意圖Fig.4 Diagram of simple support beam subjected to moving constant force

定義ζ=T1/t，t=L/v，μ=(Rd-Rj)/Rj，其中：T1為結(jié)構(gòu)的第1階固有振動(dòng)周期；t為移動(dòng)荷載通過(guò)橋梁的時(shí)間；L為橋梁的計(jì)算跨徑；Rd為跨中振動(dòng)響應(yīng)最大值；Rj為跨中最大靜態(tài)位移；μ為位移沖擊系數(shù)。

為對(duì)比積分步長(zhǎng)內(nèi)荷載等效分解方法對(duì)計(jì)算結(jié)果的影響，分析移動(dòng)常量力以不同的ζ值通過(guò)簡(jiǎn)支梁時(shí)，跨中位移沖擊系數(shù)，分別采用解析法、Runge-kutta法(解析方程數(shù)值解)、Newmark-β法(全自由度和模態(tài)綜合疊加兩種方法)、精細(xì)積分法(積分步長(zhǎng)內(nèi)荷載的協(xié)調(diào)分解及不變常量)求解。簡(jiǎn)支梁橋結(jié)構(gòu)參數(shù)，L=30m，ρ=2 600kg/m3，A=1.062 2m2，I=0.509 2m4，E=3.5·1010N/m2，移動(dòng)常量力P=3.278·1010N。

表1列出了PIM法與Newmark-β法計(jì)算跨中節(jié)點(diǎn)位移沖擊系數(shù)與參考文獻(xiàn)對(duì)比結(jié)果。其中：exact[1]結(jié)果為簡(jiǎn)支梁取前10階模態(tài)的解析解；full-size[13]結(jié)果是采用全自由度直接耦合方法計(jì)算所得；而Newmark-β[12]結(jié)果是利用ANSYS將簡(jiǎn)支梁離散成有限元模型，提取前十階模態(tài)向量計(jì)算所得；PIM-Cotes-Harmonize(PIM-C-H)法，荷載在積分步長(zhǎng)內(nèi)等效協(xié)調(diào)分解(Harmonize)，采用精細(xì)積分法(PIM)，結(jié)合科茨積分格式(Cotes)求解；PIM-Cotes-Same(PIM-C-S)法，積分步長(zhǎng)內(nèi)荷載為不變常量，采用精細(xì)積分法，結(jié)合科茨積分格式；PIM-Gauss-Same(PIM-G-S)法，積分步長(zhǎng)內(nèi)荷載為不變常量，采用精細(xì)積分法，結(jié)合高斯積分格式(Gauss)求解。

從表1可以看出，模態(tài)綜合疊加法并結(jié)合精細(xì)積分算法，計(jì)算簡(jiǎn)支梁受移動(dòng)常量力作用，跨中位移沖擊系數(shù)與解析解最大相對(duì)誤差為1.96%；當(dāng)ζ=1.5時(shí)，各種數(shù)值算法計(jì)算的沖擊系數(shù)均與文獻(xiàn)[1]有較大偏差，其他ζ值下，各種算法的沖擊系數(shù)最大絕對(duì)誤差值為0.005 8；精細(xì)積分法的積分步長(zhǎng)內(nèi)荷載協(xié)調(diào)分解格式與積分步長(zhǎng)內(nèi)常量荷載迭代格式的誤差最大值為0.05%。積分步長(zhǎng)內(nèi)荷載為不變常量，PIM-C-H計(jì)算結(jié)果比Newmark-β法更接近解析值，且不受積分步長(zhǎng)限制，能更快收斂。

例2以圖1所示移動(dòng)彈簧質(zhì)量車(chē)模型行駛在簡(jiǎn)支梁橋上為例，分析科茨積分、待定系數(shù)法及高斯積分三種數(shù)值迭代格式求解車(chē)橋耦合振動(dòng)模型Duhamel非齊次項(xiàng)響應(yīng)的差異。簡(jiǎn)支梁橋取例1中橋梁參數(shù)，車(chē)輛參數(shù)取m1=1 425 kg，m2=32 025 kg，k1=6.5×105N/m，c1=2.1×104(N·s)/m。

圖5為采用PIM-C-H，PIM-C-S，Runge-Kutta法和Newmark-β法分別計(jì)算簡(jiǎn)支梁跨中位移響應(yīng)。從圖5中可以看出，Runge-Kutta法計(jì)算結(jié)果與PIM法及Newmark-β法偏差較大；積分步長(zhǎng)較小時(shí)， PIM-C-H法與Newmark-β法曲線重合，PIM-C-H法和PIM-C-S存在一定誤差，精細(xì)積分結(jié)合科茨積分格式，荷載分解方式對(duì)計(jì)算結(jié)果產(chǎn)生一定影響， Runge-Kutta法計(jì)算結(jié)果偏離其他三者較大。圖6為分別采用PIM-C-H法、PIM-C-S法、PIM-G-S法求解車(chē)橋耦合振動(dòng)響應(yīng)曲線。圖7為采用PIM-G-H法求解車(chē)橋耦合振動(dòng)響應(yīng)。從圖6和圖7中可以看出，積分步長(zhǎng)內(nèi)荷載為不變常量，精細(xì)積分法的特解采用Gauss或Cotes迭代格式，兩者計(jì)算結(jié)果完全吻合；但考慮積分步長(zhǎng)內(nèi)荷載協(xié)調(diào)分解，Gauss算法發(fā)散，文獻(xiàn)[11]針對(duì)車(chē)橋耦合的Gauss算法提出一種預(yù)測(cè)-校正的精細(xì)積分-高斯積分格式，三節(jié)點(diǎn)高斯積分格式求解任意荷載形式的車(chē)橋耦合振動(dòng)特解需進(jìn)行校正。采用待定系數(shù)法計(jì)算車(chē)橋耦合振動(dòng)響應(yīng)，因待定系數(shù)法需對(duì)矩陣求逆，計(jì)算結(jié)果雖不發(fā)散，但曲線明顯與實(shí)際不符。

表1 移動(dòng)集中力通過(guò)簡(jiǎn)支梁橋，跨中位移沖擊系數(shù)對(duì)比表

Tab.1 Contrast table of Impact factors of the simple supported beam with mobile concentration force

T1/t①exact[1]②lin[14]③full-size[13]④Runge-Kuta[12]⑤Newmark-β[12]⑥PIM-C-S⑦PIM-C-H(⑦-①)/①(%)0.10.0500.0530.0650.0480.0510.0510.0511.600.50.2500.2520.2560.2550.2560.2550.2551.961.00.7070.7050.7030.7050.7020.7030.703-0.521.2340.7430.7300.7370.7320.7320.7330.733-1.401.50.7100.7040.6950.7020.6990.6990.699-1.512.00.5500.5500.5490.5500.5500.5500.550-0.04

(⑦-①)/①%為PIM-C-H法計(jì)算結(jié)果與精確值誤差。

圖5 不同算法分析跨中位移響應(yīng)Fig.5 Displacement curve of dynamic response at mid span using different numerical algorithm

圖6 精細(xì)積分法不同特解迭代格式跨中位移響應(yīng)Fig.6 Dynamic displacement response of at mid span using different PIM integral formulation

根據(jù)上文分析，Newmark-β法、PIM-C-S法、PIM-G-S法、PIM-C-H法能有效計(jì)算車(chē)橋耦合振動(dòng)響應(yīng)，表2分析了這4種方法計(jì)算移動(dòng)彈簧質(zhì)量車(chē)模型行駛在簡(jiǎn)支梁橋上，積分步長(zhǎng)對(duì)程序計(jì)算時(shí)間、收斂速度及跨中最大動(dòng)撓度的影響。從表2可以看出，相同積分步長(zhǎng)，Newmark-β法計(jì)算精度遠(yuǎn)小于PIM-C-H法，但相同積分次數(shù)，其運(yùn)行時(shí)間較PIM-C-H法少；在保證相同計(jì)算精度條件下，PIM-C-H法能快速穩(wěn)定。精細(xì)積分法，在單元節(jié)點(diǎn)荷載等效時(shí)，若不考慮荷載在積分步長(zhǎng)內(nèi)協(xié)調(diào)分解，采用高斯積分格式和科茨積分格式，計(jì)算誤差均較Newmark-β法大，但考慮積分步長(zhǎng)內(nèi)荷載按協(xié)調(diào)分解，誤差最小。同時(shí)，從解的穩(wěn)定性來(lái)看，相同行車(chē)速度下，Newmark-β法需PIM-C-H法近10倍的積分步、3倍的計(jì)算時(shí)間方可達(dá)到相同的穩(wěn)定解，PIM-C-H具有快速收斂，但相同積分步長(zhǎng)，計(jì)算時(shí)間較長(zhǎng)。

圖7 PIM-G-H法分析跨中位移響應(yīng)Fig.7 Dynamic displacement response of at mid span using PIM-G-H method

車(chē)速/(m·s-1)①Newmark-β法②PIM-Gause-Same③PIM-Cotes-Same④PIM-Cotes-Harmonize總積分步最大動(dòng)位移/mm計(jì)算時(shí)間/s總積分步最大動(dòng)位移/mm計(jì)算時(shí)間/s總積分步最大動(dòng)位移/mm計(jì)算時(shí)間/s總積分步最大動(dòng)位移/mm計(jì)算時(shí)間/s530060012006000120006000011.055611.255111.323311.343911.344211.34440.132760.263770.523492.533455.0332324.968523006001200600010.770610.778510.779210.78010.466340.903471.766798.729323006001200600010.764910.778410.779210.78010.447050.853221.715318.550273006001200600011.151711.337411.345011.34440.504381.007881.962179.7721015200400200040002000010.853910.863710.874410.874810.87500.097730.177870.848261.678378.203842004002000400010.690910.689310.691010.69100.300760.589762.966645.842892004002000400010.690910.689310.691010.69100.302890.585632.879125.66656200400200010.876210.874310.87500.346480.666613.3646530100200100020001000011.305511.250011.254511.253811.25360.055010.101210.434340.849154.234131002001000200011.121311.126111.128511.12850.155880.296851.479052.957111002001000200011.121311.126111.128511.12850.154360.294401.417612.931651002001000200011.254711.258511.253711.25560.179260.343891.685213.31891

4 結(jié)束語(yǔ)

結(jié)合模態(tài)綜合疊加技術(shù)，建立了移動(dòng)彈簧質(zhì)量車(chē)橋耦合振動(dòng)模型，考慮積分步長(zhǎng)內(nèi)荷載按協(xié)調(diào)分解和不變常量?jī)煞N格式，等效引入精細(xì)積分法，研究Duhamel非齊次項(xiàng)積分格式對(duì)簡(jiǎn)支梁跨中位移響應(yīng)的影響。研究結(jié)果表明：

1) 精細(xì)積分結(jié)合科茨積分格式計(jì)算移動(dòng)常量力作用下車(chē)橋耦合振動(dòng)響應(yīng)，協(xié)調(diào)分解值與解析值更接近；積分步長(zhǎng)較小時(shí)，Newmark-β法積分步內(nèi)荷載可按常量處理。

2) 精細(xì)積分法結(jié)合高斯積分考慮荷載協(xié)調(diào)分解，求解車(chē)橋耦合振動(dòng)響應(yīng)呈發(fā)散趨勢(shì)。

3) Newmark-β法能滿足工程需要，但為保證其計(jì)算精度，需較小的積分步長(zhǎng)、且耗費(fèi)較多的計(jì)算時(shí)間。

4) 精細(xì)積分法求解車(chē)橋耦合振動(dòng)響應(yīng)，采用科茨積分格式，計(jì)算結(jié)果不受積分步長(zhǎng)的影響，考慮積分步內(nèi)荷載協(xié)調(diào)分解，計(jì)算精度高，PIM-C-H法具有快速收斂且計(jì)算較快的優(yōu)勢(shì)。

[1] Henchi K, Fafard M,Talbot M,et al. An efficient algorithm for dynamic analysis of bridges under moving vehicles using a coupled modal and physical components approach[J]. Journal of Sound and Vibration, 1998 ,212(4):663-683.

[2] 翟婉明. 車(chē)輛-軌道耦合動(dòng)力學(xué)[M].北京：科學(xué)出版社，2007:1-8.

[3] 鐘萬(wàn)勰. 結(jié)構(gòu)動(dòng)力方程的精細(xì)時(shí)程積分法[J].大連理工大學(xué)學(xué)報(bào)，1994, 32(2):131-136.

Zhong Wanxie. On precise time-integration method for structural dynamics [J]. Journal of Dalian University of Technology, 1994, 32(2):131-136.(in Chinese)

[4] 譚述君, 高強(qiáng), 鐘萬(wàn)勰. Duhamel 項(xiàng)的精細(xì)積分方法在非線性微分方程數(shù)值求解中的應(yīng)用[J].計(jì)算力學(xué)學(xué)報(bào),2010, 27(5):752-758.

Tan Shujun, Gao Qiang, Zhong Wanxie. Application of Duhamel term′s precise integration method in solving nonlinear differential equations[J]. Chinese Journal of Computational Mechanics, 2010, 27(5):752-758. (in Chinese)

[5] 高強(qiáng), 吳鋒, 張洪武,等. 大規(guī)模動(dòng)力系統(tǒng)改進(jìn)的快速精細(xì)積分方法[J].計(jì)算力學(xué)學(xué)報(bào), 2011，28(4):493-498.

Gao Qiang, Wu Feng, Zhang Hongwu, et al. A fast precise intergration method for large-scale dynamic structures[J].Chinese Journal of Computational Mechanics, 2011，28(4):493-498. (in Chinese)

[6] 張文志, 富明慧, 劉祚秋. 結(jié)構(gòu)動(dòng)力方程的精細(xì)積分-FFT方法[J].中山大學(xué)學(xué)報(bào)：自然科學(xué)版,2008, 47(6):12-15.

Zhang Wenzhi, Fu Minghui, Liu Zuoqiu. Precise integration-FFT method for structural dynamics[J]. ACTA Scientiarum Naturalium Universitatis Sunyatseni, 2008,47(6):12-15. (in Chinese)

[7] 汪夢(mèng)甫, 周錫元. 結(jié)構(gòu)動(dòng)力方程的高斯精細(xì)時(shí)程積分法[J]. 工程力學(xué), 2004, 21(4):13-16.

Wang Mengfu, Zhou Xiyuan. Gauss precise time-integration of structural dynamic analysis[J]. Engineering Mechanics, 2004, 21(4):13-16. (in Chinese)

[8] 富明慧，劉祚秋, 林敬華. 一種廣義精細(xì)積分法[J]. 力學(xué)學(xué)報(bào), 2007, 39(5):72-77.

Fu Minghui, Liu Zuoqiu, Lin Jinhua. A generalized precise time step integration method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5):72-77. (in Chinese)

[9] 儲(chǔ)德文, 王元豐. 精細(xì)直接積分法的積分方法選擇[J]. 工程力學(xué), 2002，19(6):115-119.

Chu Dewen, Wang Yuanfeng. Integration formula selection for precise direct integration method[J]. Engineeying Mechanics, 2002,19(6): 115-119. (in Chinese)

[10] 黃濤, 樊建平, 何建平,等. 求解非線性動(dòng)力學(xué)方程的預(yù)測(cè)-校正數(shù)值算法[J]. 固體力學(xué)學(xué)報(bào), 2007,28(1):1-6.

Huang Tao, Fan Jianping, He Jianping, et al. A predict-correct numerical integration scheme for solving nonlinear dynamic equations[J]. Acta Mech Anica Solida Sinica, 2007,28(1):1-6. (in Chinese)

[11] 杜憲亭, 夏禾, 李慧樂(lè),等. 基于改進(jìn)高斯精細(xì)積分法的車(chē)橋耦合振動(dòng)分析框架[J]. 工程力學(xué), 2013，30(9):171-176.

Du Xianting, Xia He, Li Huile, et al. Dynamic analysis framework of train-bridge system based on improved gauss precise integration method[J]. Engineering Mechanics, 2013，30(9):171-176. (in Chinese)

[12] 王運(yùn)金，桂水榮，陳水生.連續(xù)梁橋車(chē)橋耦合振動(dòng)分析的數(shù)值解法[J]. 華東交通大學(xué)學(xué)報(bào)，2007,24(4):25-29.

Wang Yunjin，Gui Shuirong，Chen Shuisheng. An efficient algorithm for coupled vibration analysis of continuous bridges under moving vehicle[J]. Journal of East China Jiaotong University，2007,24(4):25-29. (in Chinese)

[13] 陳水生. 公路車(chē)橋耦合振動(dòng)響應(yīng)計(jì)算方法對(duì)比研究[J].華東交通大學(xué)學(xué)報(bào)，2011, 28(3):18-25.

Chen Shuisheng. Comparative research on the calculating methods for coupling highway vehicle-bridge system[J]. Journal of East China Jiaotong University, 2011, 28(3):18-25. (in Chinese)

[14] Lin Y H,Trethewey M W. Finite element analysis of elastic beams subjected to moving dynamic loads[J]. Journal of Sound and Vibration, 1990,136(2):323-342.

國(guó)家自然科學(xué)基金資助項(xiàng)目(51468018 ,51268013)；江西省教育廳科研資助項(xiàng)目(GJJ14384)；教育部工程研究中心資助項(xiàng)目(13TM02)

2015-07-17；

2016-04-18

U441.3; TH.3

桂水榮，女，1979年10月生，博士生、副教授。主要研究方向?yàn)楣窐蛄很?chē)橋耦合振動(dòng)。曾發(fā)表《系桿拱橋吊桿節(jié)點(diǎn)足尺模型承載性能試驗(yàn)研究》(《橋梁建設(shè)》2013年第43卷第2期)等論文。

E-mail:guishuirong@163.com