電火花機床主軸頭的模態分析與減振設計

王 民， 牛煥煥， 高相勝， 王敏達

(北京工業大學先進制造技術北京市重點實驗室 北京，100124)

10.16450/j.cnki.issn.1004-6801.2017.05.008

電火花機床主軸頭的模態分析與減振設計

王 民， 牛煥煥， 高相勝， 王敏達

(北京工業大學先進制造技術北京市重點實驗室 北京，100124)

針對某機床廠生產的SH50電火花機床在實際工作中主軸頭振動較大的問題，通過實驗測試和有限元仿真相結合的方法，分析了主軸頭的模態特性，并通過測試主軸頭的工作振型(operating deflection shapes，簡稱ODS)，找出了主軸頭實際工作中的薄弱環節。理論模態、實驗模態和ODS三種結果相互印證，增加了有限元模型的可信度，并以此模型為基礎對主軸頭進行了減振設計。模態實驗中改進了傳統模態實驗依靠經驗選取測點或均勻布點時，對經驗高度依賴且實驗效率較低的弊端，采用有效獨立法和模態置信度(modal assurance criterion，簡稱MAC)矩陣相結合的方法，實驗前先進行測點優化，然后根據優化結果布置傳感器和力錘位置，提高了模態實驗的精度和效率。結果顯示，在主軸頭結構上增加一個背板，能夠提高主軸頭頻率，遠離工作頻率的共振范圍，起到減振的目的。

機床； 模態分析； 測點優化； ODS分析； 減振設計

引 言

隨著模具加工的不斷發展和難加工、高性能材料的不斷出現，制造行業對機床綜合性能的要求不斷提高。電火花加工憑借其切削加工力小、加工精度較高、能夠實現對超硬材料及復雜零件加工的特點，越來越受到國內外制造領域人士的廣泛關注。電火花加工是一個動態過程，加工過程中的振動對工件的表面質量、加工效率、穩定性及工具電極的使用壽命等都有很大影響。因此有必要對電火花機床的動態特性進行研究，以期能夠提高機床的綜合性能，改善其加工精度和效率[1]。

機械結構的動態特性包括模態、阻尼、動剛度等，通過對機床進行模態測試可以獲得機床的動態參數。為了快速獲得準確的模態參數，激勵點和響應點的選取至關重要[2]。目前大多數數控機床模態實驗的激勵點選擇主要依靠工程經驗，這不僅會延長模態實驗的預實驗時間，而且激勵點的位置選擇具有很大的隨意性，若工程經驗不足往往會漏掉某些重要模態。數控機床模態實驗中響應測點布置方法主要采取均勻布點，均勻布點的缺點是需要大量的測試傳感器，實驗成本高。響應測點間的間距又需要很強的工程經驗來確定，測點間距過大會影響結構的振型的判斷；測點間距過密會增加模態實驗時間和實驗成本。

Kammer[3]提出可以用有效獨立法來確定一組不依賴于經驗的最佳響應自由度。根據每個候選響應點對模態向量矩陣的秩的貢獻，逐步刪除貢獻最小的自由度，直到剩下想要數量的自由度。陳鋒等[4]基于MAC矩陣，采用逐步累積法對空間橋梁載荷識別中的測點位置和數量進行了優化，提高了實驗識別的精度和效率，降低了實驗對工程經驗的依賴。Stephan[5]利用Fisher信息矩陣，通過減少自由度間的冗余，提出一種能確定飛機最佳響應自由度的方法。通過該方法選取的自由度，不僅對模態振型貢獻較大，且分布較均勻，避免了測點集中分布的弊端。

為了準確獲得SH50機床主軸頭的模態特性和ODS振型，筆者首先利用有效獨立法和MAC矩陣相結合的方法，經ANSYS分析和Matlab迭代計算，進行模態實驗前的測點優化，根據優化的測點數量和位置做模態實驗和工作振型測試，得出結構的模態參數和工作振型；然后，通過模態實驗結果和ODS結果驗證有限元模型；最后，根據ODS分析得出的主軸頭振動較大的原因，通過Isight優化平臺對有限元模型進行結構優化，給出了機床主軸頭減振設計的合理方案，并通過有限元仿真驗證了減振設計的有效性。

1 主軸頭模態分析

1.1 理論模態分析

1.1.1 主軸頭有限元建模

圖1所示為SH50機床的主軸頭部分，主要由滑座、轉接板、AR軸、直線模組、旋轉頭和電機組成。

首先，對主軸頭進行理論模態分析，對主軸頭三維模型進行結構簡化，刪除對結構動態性能影響不大的小孔、鈑金殼、圓角、倒角等小特征，以免影響網格劃分的質量。然后，將簡化后的模型導入ANSYS Workbench軟件進行模態分析。外購件和標準件采用賣家提供的材料屬性，其余零件采用灰鑄鐵材料。網格劃分方式為自由網格劃分，所有結合面均采用默認的Bonded連接方式。

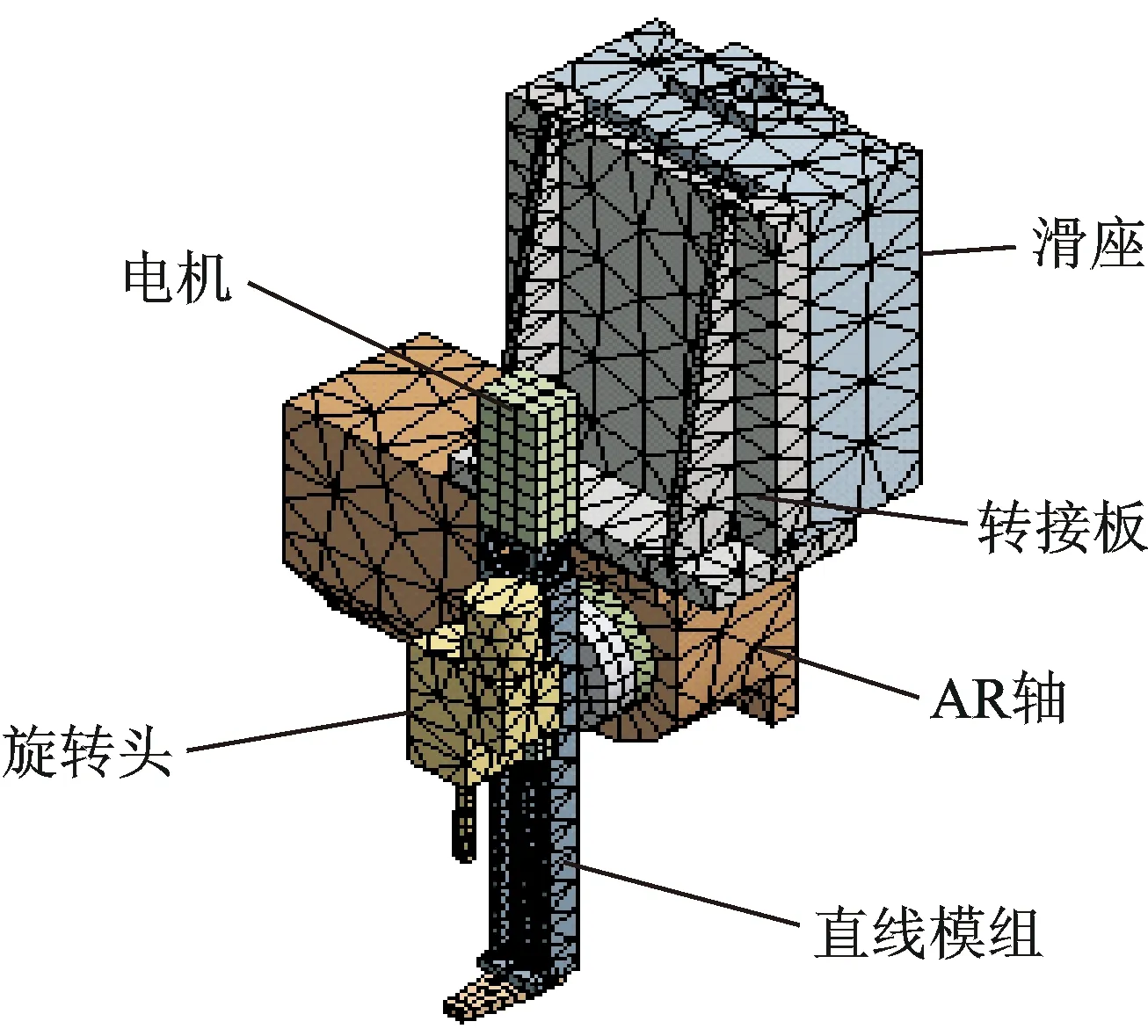
圖1 SH50機床主軸頭網格劃分模型Fig.1 Meshing model of SH50 EDM spindle

1.1.2 主軸頭理論模態分析

本次研究主要關心機床的低階模態，所以設置要求解的模態數目為5，設置主軸頭裝配體的支撐方式為滑座底面上與滑塊配合的16個孔邊線為固定約束。求解可得到主軸頭前五階固有頻率和模態振型，具體結果如表1所示。

表1 主軸頭理論模態

1.2 實驗模態分析

1.2.1 傳感器測點優化

為了改進傳統模態實驗精度受測點選取影響導致的精度和效率較低的弊端，本次模態實驗前進行測點位置的優化選取，以提高實驗的精度和效率。本次測點優化采用的方法是Kammer提出的有效獨立法，它是根據每個候選響應點對目標模態矩陣的秩的貢獻，來確定一組不依賴于經驗的最佳響應自由度[6]。通過有效獨立法雖然可以確定一組不依賴于經驗的最佳響應自由度，但對于這組最佳自由度的數目卻無法確定，因此又引入MAC矩陣的概念

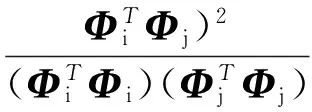
(1)

其中：Фi和Фj分別表示第i階和第j階模態向量。

MAC矩陣非對角元元素代表了對應兩階模態向量的交角狀況。若兩個向量正交，那么MAC值應該接近于0，若兩個向量完全相關，則MAC值應該接近于1。要想最大程度地保留振型特征，MAC矩陣非對角元元素越小越好。通過對模態矩陣求MAC矩陣，找出MAC非對角元元素最大值最小時所對應的自由度數，即為測點優化的自由度數。通過MATLAB程序輸出給定數量的自由度編號，對應到ANSYS模型中的節點位置和方向，即可達到測點優化的結果。

以滑座為例，首先通過有限元分析獲得前5階的模態振型矩陣，然后根據有效獨立法和MAC矩陣相結合的方法在Matlab中進行迭代計算，可得到如圖2所示的變化曲線。由圖2可知，當自由度為3時,滑座MAC矩陣非對角元最大值達到極小值，即最少在滑座上布置3個傳感器測得的模態參數的效果最佳。顯然，這3個測點的優化結果雖然能夠識別出固有頻率，但無法準確識別前5階模態振型，因此有必要再適當增加一些測點， 以達到振型識別的要求。使用香農定理進行增設測點的方法為：測得結構關心模態的最高頻率，估計該最高頻率的半波長；在半波長的每個節點上布置一個傳感器；再在半波長上等均布兩個傳感器[7]。

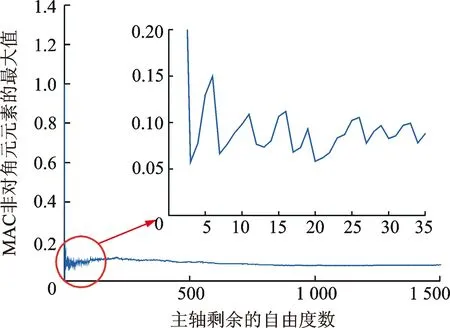
圖2 滑座MAC矩陣最大非對角元元素的最大值與滑座自由度數的變化曲線Fig.2 Variation curve of the maximum off-diagonal elements of the MAC matrix with the DOFs of the slide

機床主軸頭滑座的長邊為350 mm，通過有限元分析獲得第5階固有頻率下滑座的一條長邊的節點位移，再將其進行曲線擬合得到滑座變形最大的x方向上的位移波形如圖3，從波形估計滑座的波長λ≈700 mm。

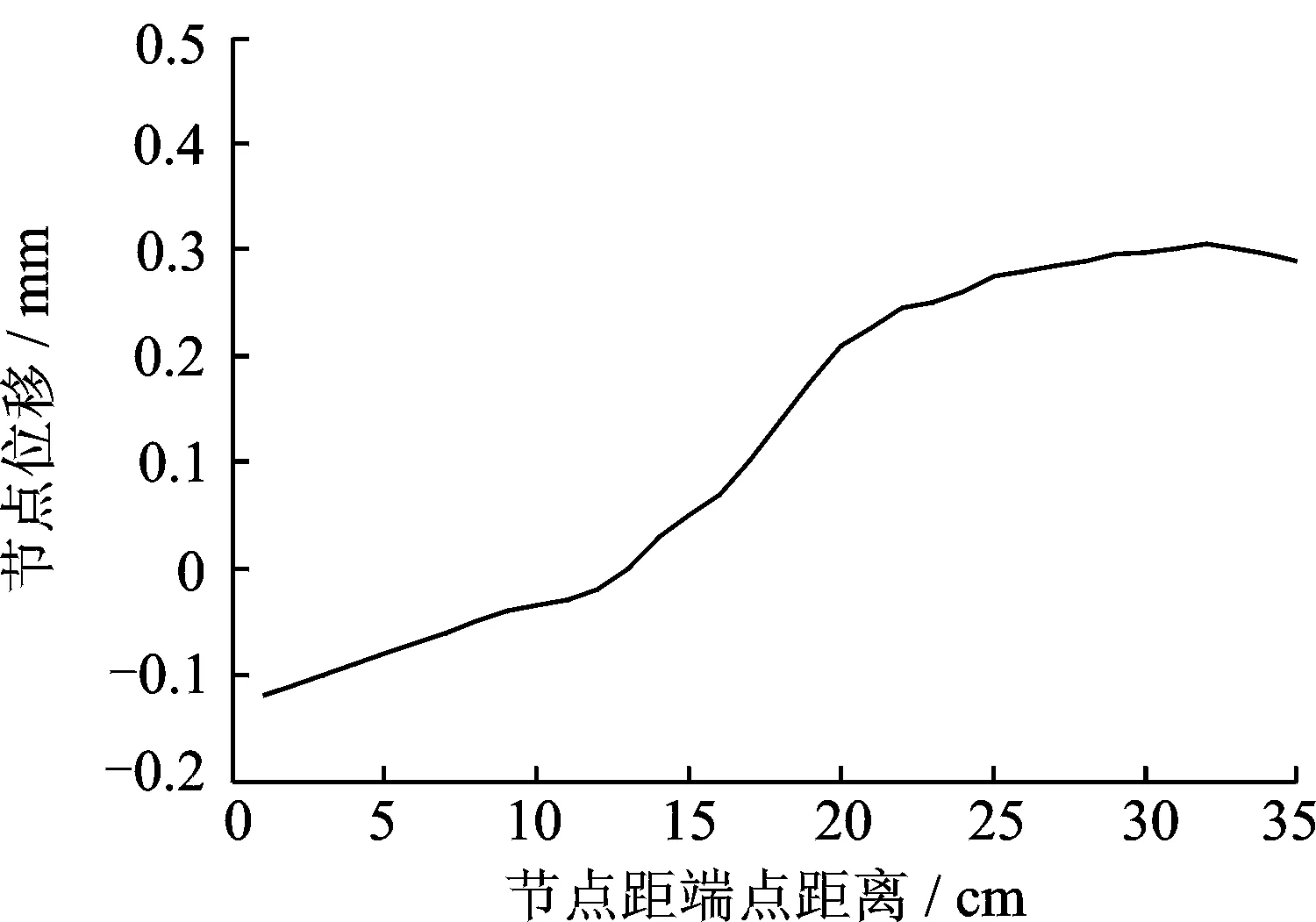
圖3 滑座第5階頻率下的長邊波形Fig.3 Waveform of the longest edge of the slide at the fifth modal frequency

使用香農定理進行增設測點后的測點優化結果見圖4所示。圖中編號為有限元分析中對應的節點編號。圖中有標號的節點為優化得到的節點，無標號的節點為通過香農定理增加的節點。通過對比圖4和滑座前5階振型，發現通過這種方法選擇的測點大都分布在零件變形較大的部位，因此這樣選擇的測點對模態振型的貢獻最大，且滿足振型識別的要求。同理，對主軸頭其他關鍵結構也可以通過這種方法進行測點優化。

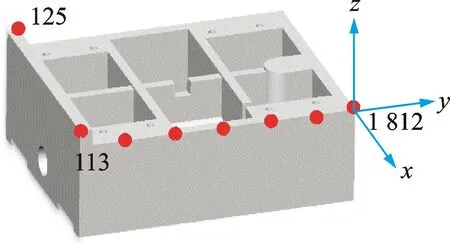
圖4 滑座測點優化結果Fig.4 Optimal sensors placement of the slide

1.2.2 主軸頭模態測試

本次模態實驗使用的是丹麥B&K 公司的模態測試分析系統，采用單點拾振多點激勵測試方法，即將加速度傳感器固定于主軸頭下端，用帶有力傳感器的力錘在選定的位置敲擊試件，給試件一個激振力。力信號和響應信號經數據采集前端被送入計算機中的PULSE 分析儀中，經數據處理軟件ME′scopeVES分析計算，得出試件頻響函數及模態參數。圖5為在模態測試軟件中建立的主軸頭測試模型，紅色箭頭表示加速度傳感器測試位置及方向，黑色箭頭表示力錘激振位置及方向。

根據Maxwell互異性原理，在P點輸入所引起的在Q點的響應，等于在Q點相同輸入的P點的響應[8]。因此，激勵點可從優化得到的響應測點中選取，對響應測點的優化亦即對激勵點的優化。

通過對比實驗模態和有限元模態，發現實驗結果中沒有與有限元第3、第4階振型相對應的模態。仔細觀察有限元振型可知，第3，4階振型是在第2階模態的基礎上，增加了旋轉頭部分的振動，可以認為是旋轉頭的局部模態。因此取129.12,140.37和200.49 Hz為主軸頭前3階理論模態。實驗測得的模態參數與理論值的比較結果如表2所示。

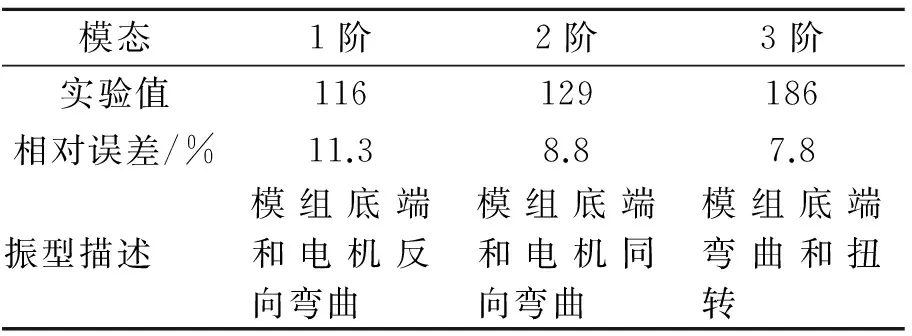
表2 模態測試結果

由表2對比結果可以發現，有限元得到的結果與模態測試得到的結果誤差都在15%以下，滿足工程誤差的要求。實驗結果驗證了有限元模型的有效性，因此可以用有限元模型對結構進行仿真優化。

2 主軸頭ODS分析與減振設計

2.1 主軸頭ODS分析

2.1.1 ODS分析理論

傳統的模態分析試驗通常是在受控條件下進行的，然而極少有結構會在這樣的條件下工作。要想了解結構在工作狀態下的實際變形，還需要引入ODS的概念。ODS為工作狀態下的變形，表明結構在某一特定工作狀態下的振動狀態。因此，ODS也通常被稱為工作振型。ODS 不僅可以表現結構振動敏感部位的相對變形，而且可直觀地識別出故障發生位置及結構的薄弱環節。

2.1.2 ODS測試結果

本次ODS測試用機床模擬實際工況，讓電極進行上下往復運動，工作頻率為50 Hz。如果ODS展現的是ODS FRF數據塊中的共振峰值或者峰值點附近的振動動畫，則該ODS振型基本等同于模態振型[9]。將ODS分析得到的實驗結果與模態實驗分析得到的結果進行對比分析，以驗證實驗結果的可信性，然后以ODS測出的薄弱環節對結構進行減振設計。對比結果見表3，可見兩者誤差基本在工程允許范圍內，兩種結果相互印證。

表3模態實驗與ODS實驗結果對比

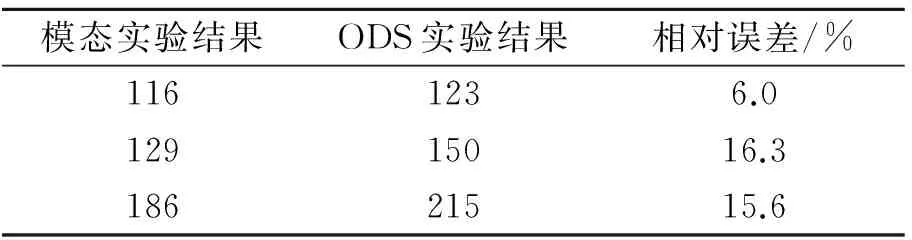
Tab．3 Comparison between modal experimental results and ODS experimental results Hz

2.1.3 ODS結果分析

將ODS實驗測得的加速度信號經兩次積分，得到主軸頭工作狀態下位移變形曲線。在位移曲線中，可找到工作狀態下主軸頭振動幅度較大所對應的頻率。取位移較大的兩點對應的頻率122和149 Hz進行分析。通過觀察122和149 Hz處的工作振型，發現它們分別與主軸頭1階、2階模態振型相似，且與主軸頭1階、2階固有頻率相差不遠，因此這兩處振動劇烈的原因是工作頻率激起主軸頭1階、2階模態所致。要想對主軸頭結構進行減振設計，需要提高主軸頭固有頻率，使其1階、2階固有頻率更加遠離工作頻率。

2.2 主軸頭減振設計

2.2.1 減振設計

經過模態分析和ODS測試，確定了主軸頭工作狀態下的薄弱環節。因為直線模組屬細長零件，剛性較差，因此減振的關鍵是提高直線模組的剛度，并盡可能提高主軸頭固有頻率。又因為直線模組是采購件，不宜對其結構進行改動。為提高直線模組剛度，決定在其后面增加一個背板，以增加主軸頭整體剛度，提高其固有頻率。

考慮直線模組安裝定位和結構之間的連接和干涉等因素，在不影響加工、方便裝配、結構之間無干涉的條件下，初步設計背板為“凵”型結構。已知直線模組軌道長寬高為400 mm×60 mm×33 mm，左右兩側的安裝定位面距底面10 mm。模組與背板之間采用底面和一側面做定位基準面，因此背板可以確定的參數長為400 mm、兩側翼緣高度為10 mm、兩側翼緣內側間距為60 mm。為便于安裝，兩側翼緣內側間距60 mm應設計出一微小間隙。背板還需要優化的參數為翼緣厚度和背板厚度。

因為機械結構的動剛度與結構有很大關系，固有頻率越高，說明單位質量的結構剛度越高[10]。在Isight優化平臺中集成SolidWorks和ANSYS文件，采用NLPQL(序列二次規劃法)法，以背板1階，2階固有頻率和背板質量為優化目標，對背板厚度和翼緣厚度進行優化。為使結構不致過重，根據工程經驗，取板厚均在3～8 mm之間進行迭代優化。最終，在滿足背板1階、2階固有頻率較大和質量較小的條件下，折中選取背板厚度為5.2 mm，翼緣厚度為7.8 mm，優化后的背板結構和主軸頭裝配圖見圖6所示。背板和模組之間通過底面上均布的8個螺栓孔連接，并通過其中4個孔與后面的轉接盤連接。

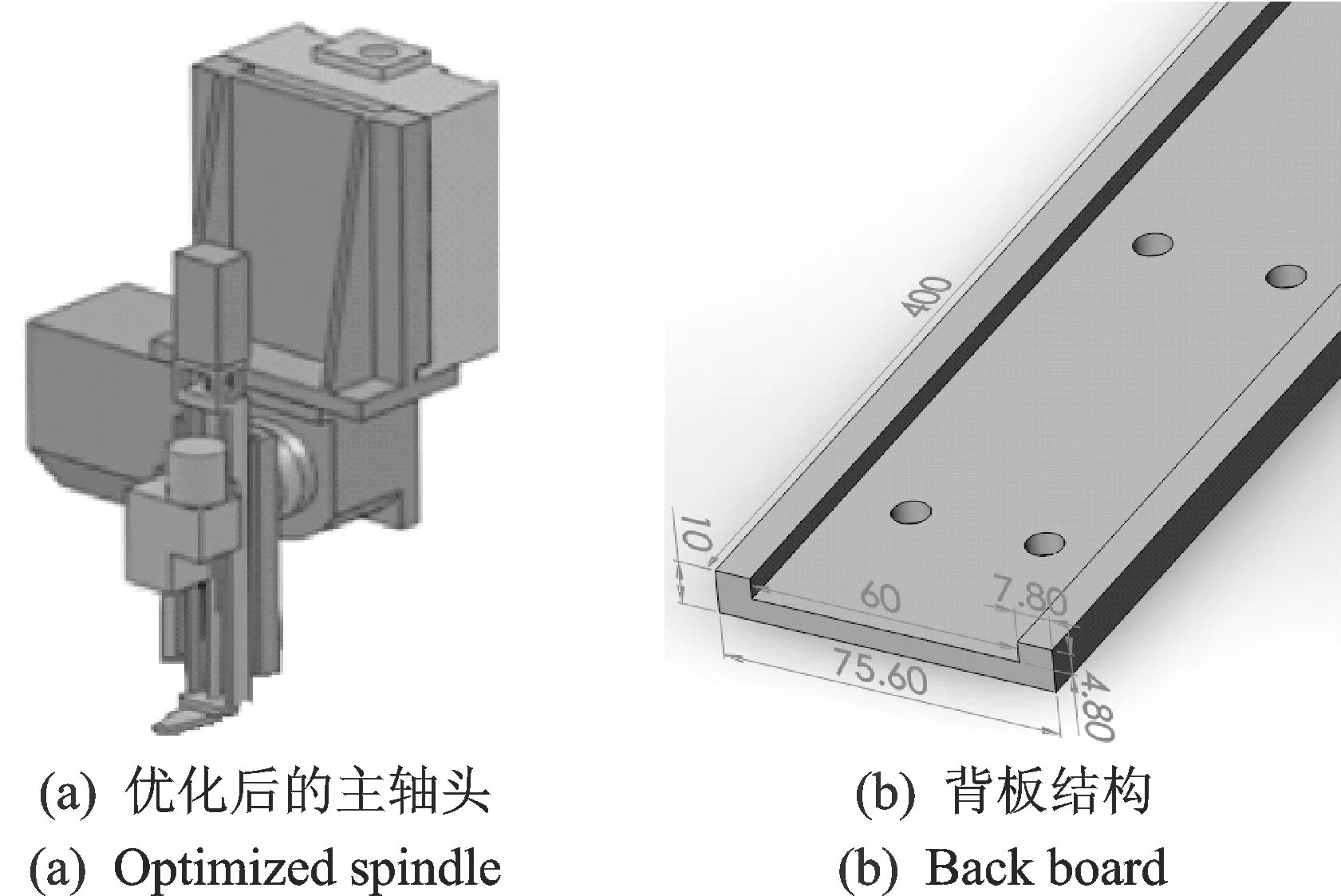
圖6 減振設計結構Fig.6 Structure of anti-vibration design

2.2.2 減振設計效果驗證

為了驗證增加背板后的減振效果，對優化后的主軸頭進行了理論模態分析，結果顯示，主軸頭的各階固有頻率都得以提升。其中1階固有頻率理論值由原來的129.12 Hz提高到162.34 Hz，2階固有頻率理論值由原來的140.37 Hz提高到183.79 Hz，3階固有頻率理論值由原來的200.49 Hz提高到283.23 Hz，都更加遠離了工作頻率，避開了工作頻率的共振范圍。主軸頭各階振型的最大變形也得以大幅度減小，達到了減振設計的優化效果。優化后的前3階振型如圖7所示。

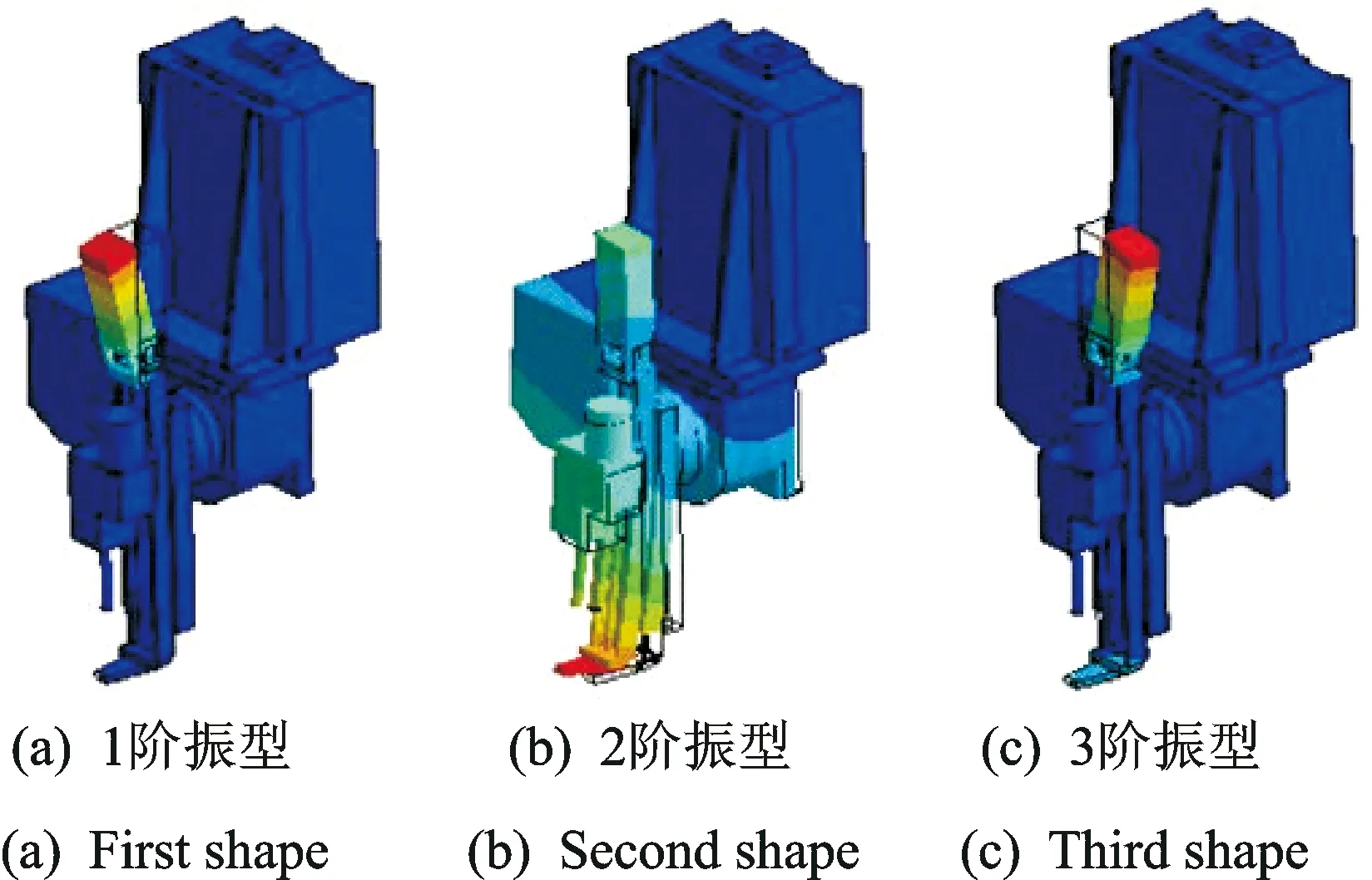
圖7 優化后結構前3階振型Fig.7 First three modal shapes of the spindle after optimization

3 結束語

筆者建立了SH50電火花機床主軸頭的三維模型和有限元模型，并對主軸頭進行了有限元模態分析。使用有效獨立法和MAC矩陣相結合的方法，對主軸頭進行了模態實驗前的測點優化，根據優化的測點對主軸頭進行了模態實驗，其結果和理論結果相互印證。在工作狀態下對主軸頭進行了ODS測試，找出了主軸頭工作狀態下的薄弱環節，并用有限元模型對主軸頭進行了減振設計，驗證了設計的有效性。

[1] 邵衛東, 李崇豪, 陳德忠. 電火花成形機主軸頭動態特性分析及振動研究[J]. 電加工, 1992(4): 2-16.

Shao Weidong,Li Chonghao,Chen Dezhong.The dynamic analysis and vibration research of EDM machine tool spindle[J].Electromachining & Mould, 1992(4):2-16.(in Chinese)

[2] 沃德·海倫, 斯蒂芬·茲. 模態分析理論與試驗[M]. 白化同,郭繼忠，譯. 北京: 北京理工大學出版社, 2001：120-156.

[3] Kammer D C. Sensor placement for on-orbit modal identification and correlation of large space structures[J]. AIAA Journal of Guidance, Control, and Dynamics, 1992,14(2)：251-259.

[4] 陳鋒, 李忠獻. 梁橋上移動荷載識別中的測點優化[J]. 振動、測試與診斷, 2009, 29(2): 218-222.

Chen Feng，Li Zhongxian.Sensor placement optimization for moving load identification on girder bridges [J]. Journal of Vibration，Measurement & Diagnosis,2009,29(2):218-222. (in Chinese)

[5] Stephan C． Sensor placement for modal identification[J]. Mechanical Systems and Signal Processing, 2017,27(1):461-470.

[6] 何云, 余文柏. 基于有效獨立法的傳感器優化布置[J]. 工程建設與設計, 2011(8): 134-136.

He Yun, Yu Wenbai. An optimal sensor placement methods based on the effective independence method[J]. Construction & Design for Engineering, 2011(8): 134-136. (in Chinese)

[7] 白向賀. 數控機床模態實驗的激勵點選擇和響應測點布置優化[D]. 武漢：華中科技大學, 2012.

[8] Schedlinski C, Link M. An approach to optimal pick-up and exciter placement[C]∥Proceedings of the 14th International Modal Analysis Conference.[S.l.]:Spie International Society for Optical,1996:376-382.

[9] 王學林, 章蘭珠, 陳學東, 等. 使用ODS FRF方法分析葉輪的動態特性[J]. 華東理工大學學報：自然科學版, 2013,39(3): 370-376.

Wang Xuelin, Zhang Lanzhu, Chen Xuedong, et al.Dynamic characteristics of impeller using ODS FRF method[J]. Journal of East China University of Science and Technology:Natural Science Edition, 2013,39(3):370-376. (in Chinese)

[10] 張憲棟, 徐燕申, 林漢元. 基于FEM的數控機床結構部件靜動態設計[J]. 機械設計, 2005, 22(5): 46-48.

Zhang Xiandong,Xu Yanshen,Lin Hanyuan.Static and dynamic design on structural components of NC machine tools based on FEM[J].Journal of Machine Design,2005,22(5):46-48. (in Chinese)

國家科技重大專項基金資助項目(2012ZX04010021-001-004)

2015-08-07；

2015-10-26

TH113； TG502

王民，男，1972年2月生，博士、教授、博士生導師。主要研究方向為制造系統監控、智能材料與結構、切削穩定性分析、遠程故障診斷和質量控制技術等。曾發表《Feasibility study of nonlinear tuned mass damper for machining chatter suppression》(《Journal of Sound and Vibration》2011,Vol. 330,No.9)等論文。

E-mail:wangm@bjut．edu．cn