基于實驗SEA方法的車內噪聲預測分析

邢 鵬， 華 林， 盧熾華， 鄧 松， 杜松澤

(1．武漢理工大學現代汽車零部件技術湖北省重點實驗室 武漢，430070)(2．武漢理工大學汽車零部件技術湖北省協同創新中心 武漢，430070)

10.16450/j.cnki.issn.1004-6801.2017.05.012

基于實驗SEA方法的車內噪聲預測分析

邢 鵬1,2， 華 林1,2， 盧熾華1,2， 鄧 松1,2， 杜松澤1,2

(1．武漢理工大學現代汽車零部件技術湖北省重點實驗室 武漢，430070)(2．武漢理工大學汽車零部件技術湖北省協同創新中心 武漢，430070)

針對車內中高頻噪聲預測分析準確性低的缺陷，提出了一種有效的基于實驗分析的有統計能量分析(statistical energy analysis,簡稱SEA)方法。首先,利用點導納平均法得到速度與力的實部，確定模態密度；其次,采用衰減法得到脈沖響應，經過Hilbert變換推論出內損耗因子；最后,利用異點導納平均法，測得帶寬內的子系統的平均能量，計算出耦合阻尼損耗因子。依托某車中高頻降噪分析測得某工況下的輸入聲載荷，將實驗測得的SEA基本參數輸入到模型中，得到駕駛員右耳處的噪聲水平，其仿真值與測試值在中高頻時吻合較好，證明了轎車模型的有效性。結果表明，基于實驗方法測得SEA3個基本參數可以綜合提高模型預測車內噪聲的準確性，具有很高的工程應用價值。

模態密度；內損耗因子；耦合損耗因子；輸入功率；導納

引 言

隨著汽車市場競爭日益激烈，人們對汽車乘坐舒適性的要求越來越高。車內噪聲水平不僅是決定乘坐舒適性的主要因素，也漸漸成為影響市場競爭力的關鍵指標。目前，應用較多的車輛噪聲分析方法有統計能量分析方法、有限元法(finite element method，簡稱FEM)、邊界元法(boundary element method，簡稱BEM)。雖然FEM及BEM在結構振動和強度建模分析等實際應用中獲得了很大成功，但在中高頻噪聲研究領域不能得到精確的分析結果。SEA方法應用于汽車噪聲分析領域彌補了FEM及BEM方法在汽車中高頻分析方面的不足，經過多年的發展，現已成為改善中高頻噪聲環境的重要方法。

目前，SEA方法的研究主要分為3類：經典SEA方法、修正SEA方法和實驗SEA方法。經典SEA方法最早是由R. H. Lyon于1962年提出，之后同T. D. Scharton及J. E. Manning對SEA方法的適用范圍和工程應用進行了深入研究。但在20世紀70年代，經典SEA方法由于其假設條件(如保守耦合、弱耦合等)的限制，其發展較為緩慢。Fahy和姚德元在英國南安普頓ISVR的技術報告中闡述了非保守耦合振子的功率流，提出了修正SEA方法。之后，盛美萍[1]提出了一種新的理論，基本思想是引入等效內損耗因子，修正保守耦合損耗因子為非保守耦合損耗因子，系統仍然使用經典的能量平衡方程來進行求解。利用這種方法得到的預測值與實驗測量值有較好的一致性，從而發展了修正SEA方法，擴大了其在結構振動噪聲分析中的應用。然而，在分析汽車振動噪聲響應的工程問題中會遇到許多復雜結構系統，SEA參數的精確確定就變得非常困難，迫切需要建立精確的汽車模型預測車內噪聲。因此，實驗SEA方法成為預測復雜結構振動響應的有利方法[2]，同時也是對修正SEA方法的補充或調整。

筆者從SEA能量平衡方程出發，對SEA基本參數進行了實驗研究。分別利用原點導納、異點導納的方法從實驗角度詳細地闡述了模態密度、內損耗因子以及耦合損耗因子的測試方法；并依托某國產車中高頻降噪分析，將實驗測得的SEA基本參數和輸入功率輸入到模型中，得到駕駛員右耳處的噪聲水平，并將仿真值與測試值進行比較，驗證SEA轎車模型的準確性。

1 SEA基本理論

對于圖1所示的分析模型，振子1和振子2之間通過耦合元件相連，其功率平衡方程可以寫為

(1)

(2)

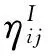
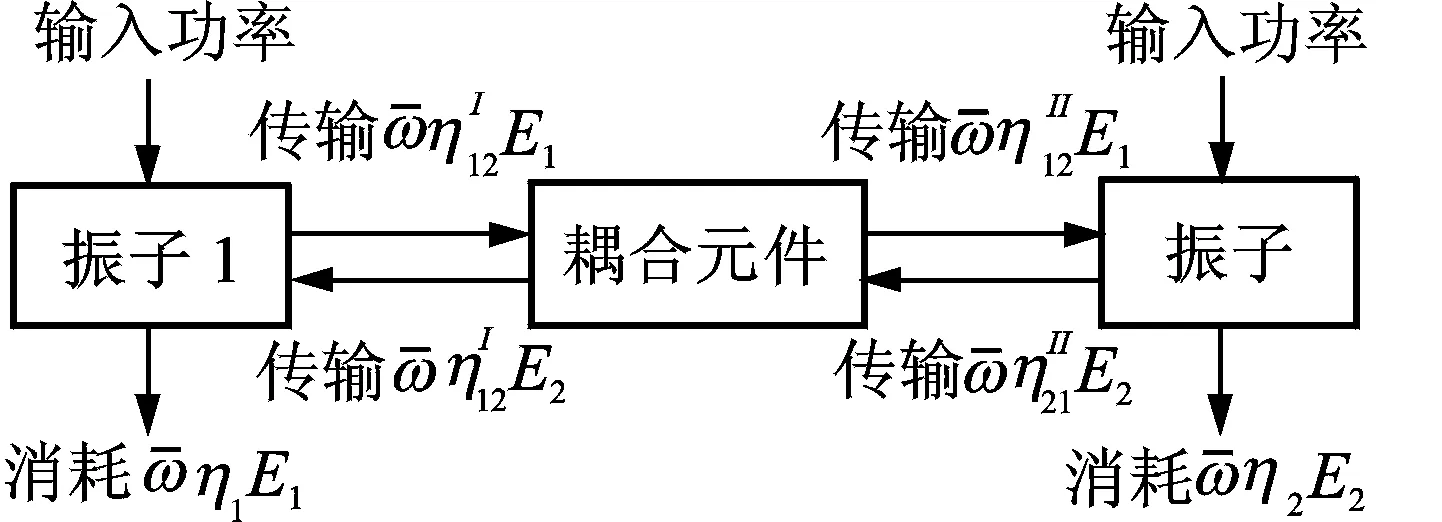
圖1 耦合系統能量統計分析模型Fig.1 Model of coupling statistical energy analysis

從方程(1)和(2)中可以看出，采用SEA方法進行計算時，關鍵是對復雜結構子系統的模態密度(多個子系統耦合時)、內損耗因子以及耦合損耗因子準確估算。利用這些參數和SEA模型的輸入功率，通過對所建立的SEA模型進行仿真計算，就可以求出目標子系統的平均能量水平，從而進一步轉換成所需要的聲壓級[3]。

2 SEA參數測試方法

2.1 模態密度

模態密度是用來描述振動系統儲存能量大小的一個物理量，是指子系統在某一頻率范圍內單位頻帶的模態數，是表征子系統在某一頻段內模態密集度的一個量[3]。

實驗測量法成為確定復雜結構模態密度的主要方法，其中點導納平均法是目前應用比較廣泛的一種實驗測量方法[1]。圖2(a)為測試車內前地板模態密度時加速度傳感器的布置。通過帶有阻抗頭的力錘，對測試地板進行錘擊[4]，依據方程(3)得到速度與力的實部導納

(3)

其中：Sff(f)為力自功率譜函數；Saf為力與加速度的互功率譜函數。

V/F和A/F分別為兩種數據導納的方法，是關于頻率的函數。當力與加速度信號是反相(這主要取決于測力計與加速度傳感器的相對定向)，那么方程(3)導納輸出的是絕對值。

根據方程(4)可獲得模態密度[5]，測試結果如圖2(b)所示。

n(f)=4m[G(f)]

(4)

其中：m為被測結構的質量。

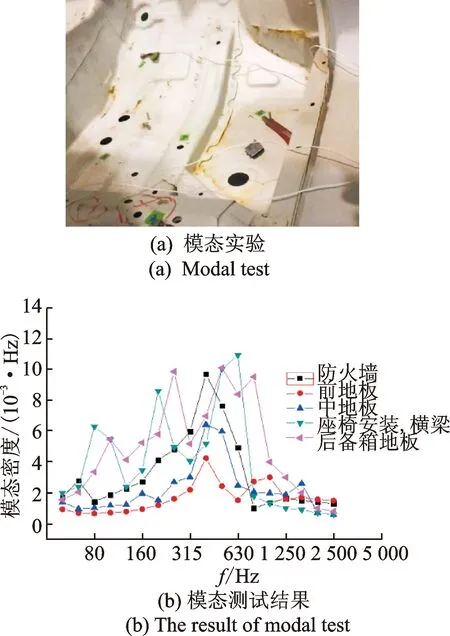
圖2 模態密度實驗及測試結果Fig.2 Modal density experiment and test results

在建立整車SEA模型時，對很多復雜結構進行了簡化，通過理論公式計算得到的模態密度曲線在各頻段內是相等的。然而，從圖2(b)可以看出，實驗測試得到的模態密度在各頻段內的數值并不相等。通過實驗測試結果對模型進行調整和修正，提高了模型對車內噪聲預測的準確性。

2.2 內損耗因子

內損耗因子(damping loss factor，簡稱DLF)是反應子系統阻尼特性的量，是指子系統在單位頻率(每振動一次)內單位時間損耗能量與平均儲存能量之比[6]。對于復雜結構的內損耗因子綜合了許多線性及非線性的能量損耗，這種損耗難以計算而必須通過測試的方法解決[7]。

筆者選擇衰減法來進行DLF的測試。衰減法是給系統施加隨機平穩激勵，然后突然撤去激勵[8]，通過分析振動衰減的規律獲得內損耗因子，如圖3(a)。它比較適用于快速估算結構和聲容積的頻帶平均內損耗因子，其統計誤差相對較小。將采集的脈沖響應利用方程(5)轉換為1/3倍頻程帶

x(t,fc,Δf)=y(t)×h(t,fc,Δf)

(5)

其中：y(t)為采集的脈沖信號；h(t,fc,Δf)為1/3倍頻濾波脈沖響應。

圖3 1 000 Hz時DLF測試結果Fig.3 The test result of DLF in 1 000 Hz

利用Hilbert變換求解瞬時信號的平均包絡線，其公式為

(6)

(7)

對一小段時間內(一般選擇20 ms)的曲線進行整合，得到比較平滑的均方衰減曲線，表達式為

e2(t→t+Δt,fc,Δf)=

e2(t,fc,Δf)·r(Δt)

(8)

其中：r(Δt)為單位向量；fc為分析頻帶的中心頻率。

以對數形式輸出均方衰減曲線，如圖3(c)所示，將曲線轉化為加速度級(dB)：

10log10(e2(t→t+Δt,fc,Δf))

(9)

最終通過衰減法推論出DLF為

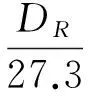
(10)

其中：η(fc,Δf)為某一系統上一個加速度計在一次激勵下的頻帶內損耗因子；DR為能量在時域曲線上衰減率。

某一子系統一次激勵采集N個加速度計的脈沖相應，可以得到一次激勵下的平均內損耗因子，為保證數據的精度，利用方程(11)可獲得子系統M次激勵下的平均DLF為

(11)

在測量DLF時選擇4 s內的脈沖信號，從圖3(b)中可以看出，0.5 s內的數據是存在很大的波動，0.5 s后的數據趨于平滑。因此筆者選擇0.5 s內衰減曲線上的數據進行最小二乘擬合，從而得到衰減率DR[2, 9]，通過式(12)可以計算出該子系統的DLF，如圖3(c)中藍線所示。圖3表示對某款車1 000 Hz頻率下前擋風玻璃進行DLF測試，并在MATLAB中將衰減曲線進行最小二乘擬合得到DLF的測量值。

2.3 耦合損耗因子

耦合損耗因子(coupling damping loss factor，簡稱CDLF)是表征耦合系統間能量交換的重要參數，它是用來表征當一個系統附接于另一個系統時的功率流或阻尼效應的量[6]。將圖4(a)測試的結果，利用方程(13)得到分析頻帶內的平均輸入導納

(12)

(13)

其中：V/F表示數據導納的形式，是關于時間的函數。

然后利用方程(14)得到帶寬內的子系統的平均能量。

(14)

其中

(15)

其中：fL分析頻帶的下限；fU為分析頻帶的上限；mk為結構子系統的質量；M為激勵次數；N為加速度傳感器的個數。

最終得到耦合損耗因子

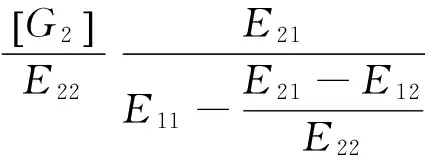
(16)

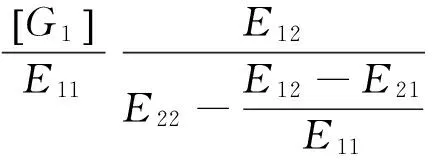
(17)

其中：GZ為系統分析頻段內的平均導納；Eij為帶寬內子系統的平均能量。

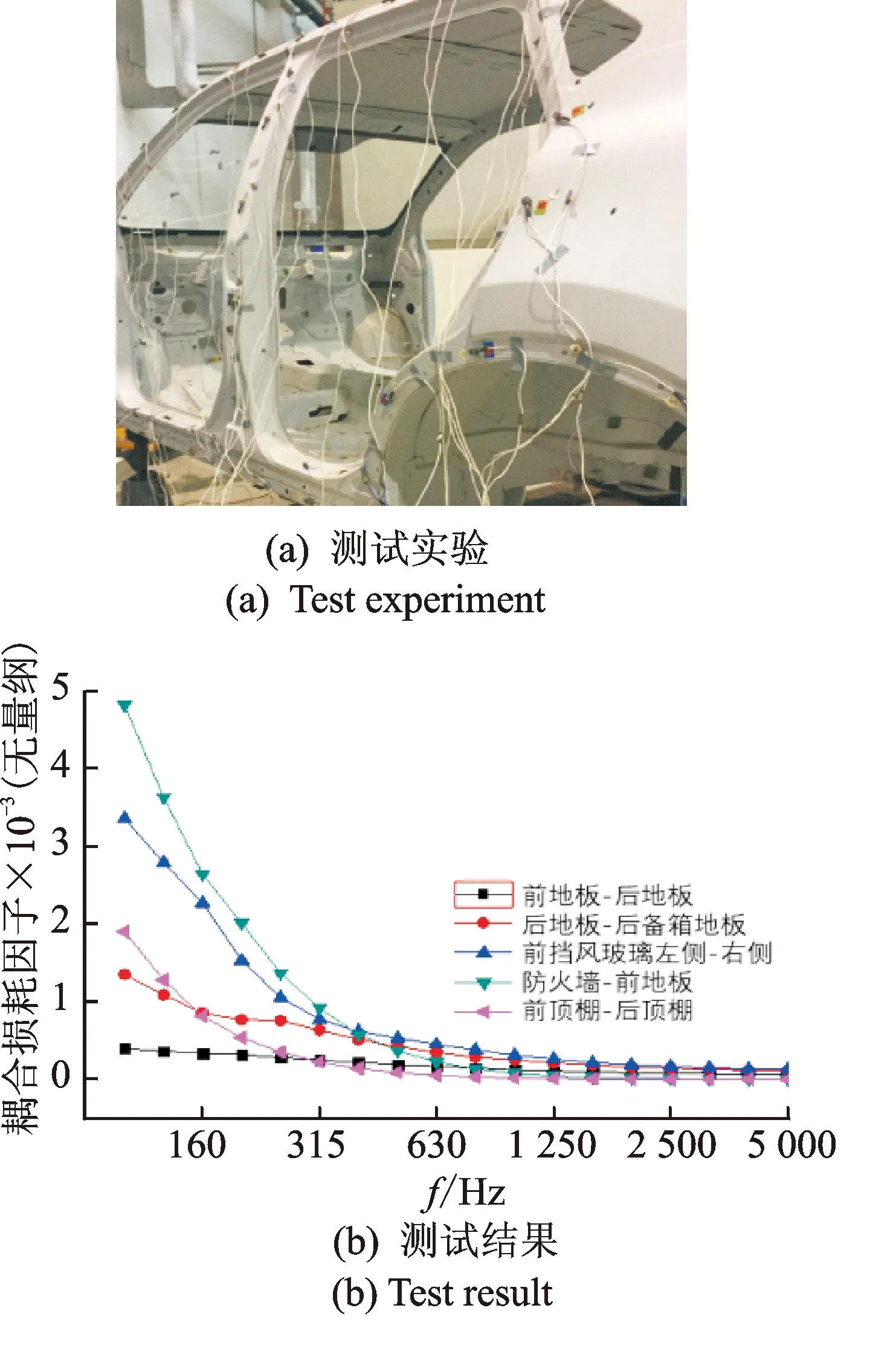
圖4 CDLF實驗及部分測試數據Fig.4 CDLF experiment and test results

從圖4(b)可看出，CDLF從數量級上比子系統的內損耗因子要小一個數量級，這對測試設備和數據采集的要求很高。由于所研究的車輛左右對稱，因此在做CDLF實驗時只對左側進行了實驗測量，并依據結果對車身結構的CDLF做了部分調整。

3 聲載荷測試

3.1 外部聲載荷測試

從方程(1，2)可知，除了模態密度、DLF，CDLF外，輸入聲載荷也是運用SEA方法進行計算的重要參數。筆者選擇在半消試驗室中測試整車某特定工況下的外部聲場聲壓值，作為SEA分析的輸入聲載荷。測試方法如圖5，6所示。

車身表面每個位置處(SEA子系統)內使用3～5個麥克風，麥克風距被測結構表面為200～250 mm，取平均得到每個位置處的聲壓值，并將其作為SEA模型的輸入聲載荷。在整個測試過程中，背景噪聲的聲壓級(sound pressure level，簡稱SPL)要比測試工況SPL至少低20 dB才能確保數據可用。整車測試區域，除發動機艙和防火墻外，認為車輛左右SPL對稱，因此測試時僅測量車輛一側，如圖6(b)所示。

圖5 麥克風布置Fig.5 Location of microphone

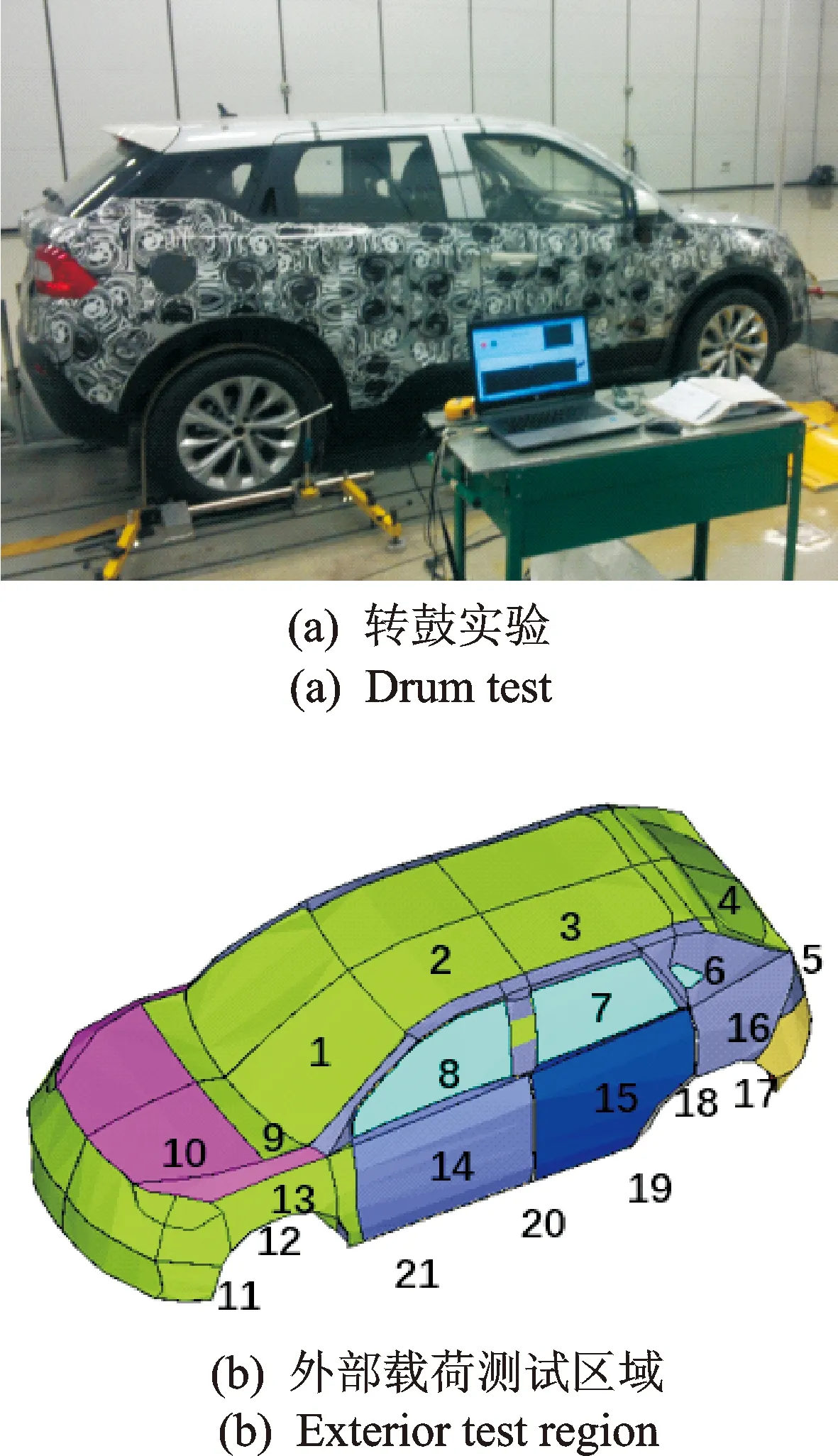
1．前擋風玻璃；2．前頂蓬；3．后頂蓬； 4．后擋風玻璃； 5．后背門； 6．后三角窗； 7．后車門玻璃；8．前車門玻璃； 9．防火墻前部； 10．發動機上部； 11．發動機下部； 12．前輪罩； 13．前翼子板；14．前車門；15．后車門； 16．后翼子板； 17．備胎輪地板； 18．左后輪罩； 19．后地板； 20．中地板； 21．前地板圖6 外部載荷測量區域FIg.6 Test region of exterior load

3.2 內部載荷測試

在測試特定工況外部噪聲的同時，測試車內SPL，如圖7所示。麥克風分別放置在駕駛員、副駕駛員和乘客所在位置的頭、腰、腿聲腔處以及后備箱聲腔，每個聲腔處有2～3個麥克風，位置如圖8所示[11]。

圖7 車內聲載荷測試Fig.7 Test of interior sound load

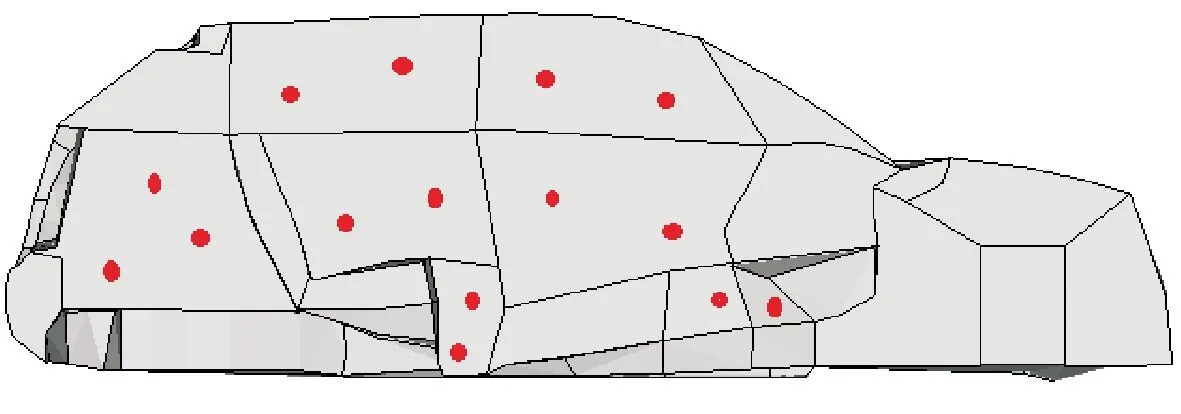
圖8 麥克風位置分布 Fig.8 Interior location of microphone

4 整車SEA分析

4.1 整車SEA建模

為驗證SEA參數測試方法的有效性，筆者依托某國產車進行實驗。將車身結構按照模態數大于5的原則將整車劃分成多個子系統[12]，得到整車SEA模型，如圖9(a)所示。基于結構子系統的節點，在車內搭建臨時板件分別建立駕駛員、副駕駛員以及中后排乘客處的頭部、腰部、腿部多個車內聲腔子系統，如圖9(b)所示[13]。同時，利用搭建完成的SEA模型節點，在車外700～1 000 mm空間內搭建臨時板件建立車外聲腔子系統，用來模擬消聲室空間結構，如圖9(c)所示。

4.2 結果分析

把所獲得的5擋100 km/h勻速行駛時的聲載荷激勵及SEA基本參數輸入到所建立的整車SEA模型中，同時將實車內飾材料的屬性參數添加到模型中，加載后對所選工況進行整車模型的仿真計算，在研究頻率范圍內(50～5 000 Hz)，駕駛員右耳旁1/3倍頻帶(1/3th qctave bands)聲壓級譜的預測值與實測值如圖10所示。

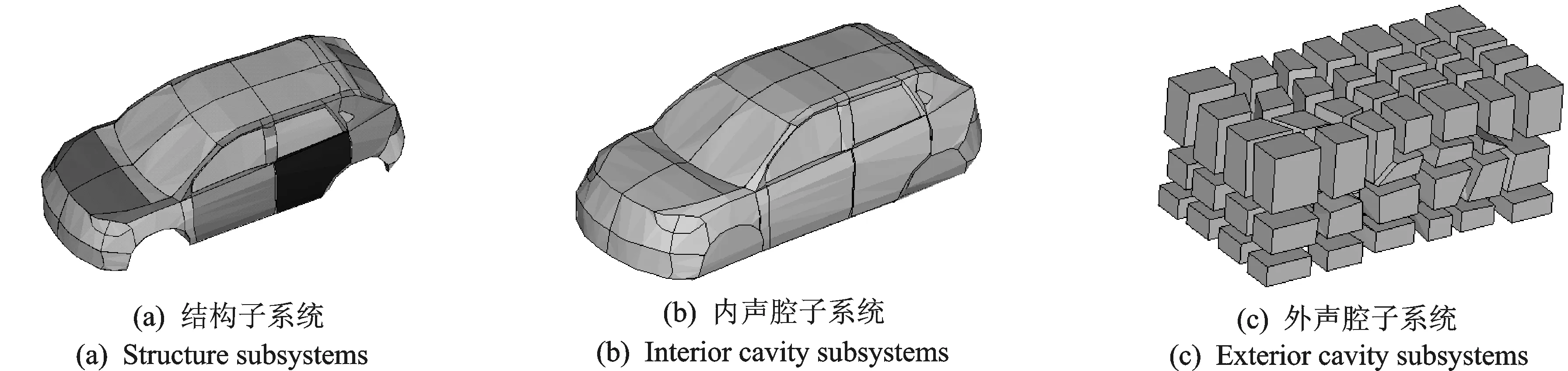
圖9 整車結構與聲腔SEA模型Fig.9 Structural and cavity model of car

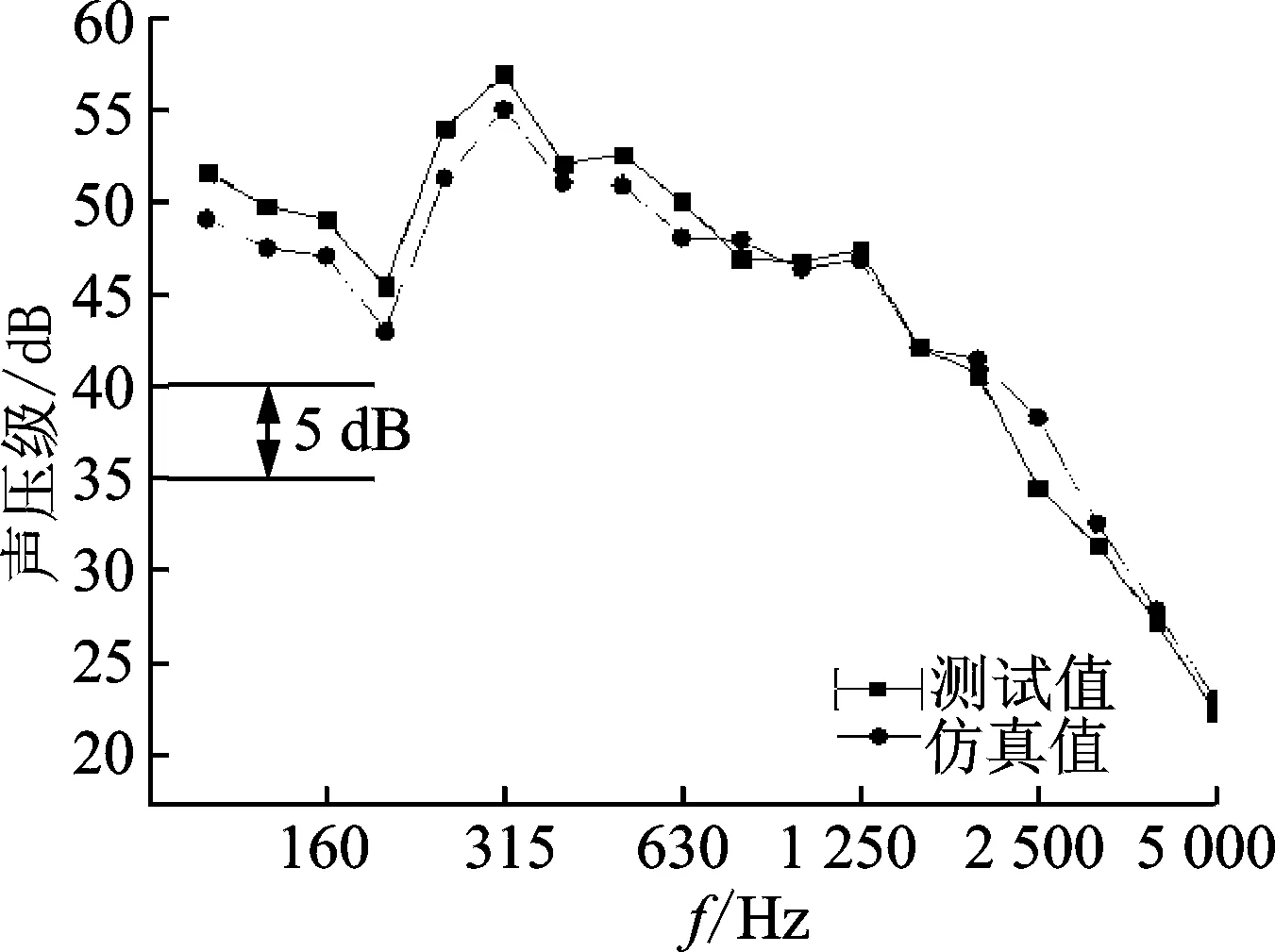
圖10 車輛以5擋100 km/h勻速行駛工況駕駛員耳旁聲壓級譜Fig.10 SPL of driver's head in 5 gear at 100 km/h

從圖10中可以看出，在低頻范圍內實測值與仿真值差別較大，這主要與SEA方法的適用范圍有關。在小于200 Hz的頻率范圍內，由于子系統的模態密度較低，致使結果在小于200 Hz的頻率范圍內出現偏差，這是低頻段內實測值與仿真值差別較大的主要原因。同時，在建立整車SEA模型時，對很多復雜結構的簡化、安裝孔的忽略以及內飾件在覆蓋率上的粗略估計，都會不同程度的影響高頻段內預測結果的準確性。在本研究的頻率范圍內(大于200 Hz)，通過實驗方法對模型進行調整，消除因模型簡化等原因造成的高頻段內誤差，最終得到的仿真值與實測值吻合較好，誤差控制在3 dB內。這說明將實驗測得的SEA基本參數應用在整車SEA中高頻仿真分析，模擬整車實際行駛工況的方法是可行的，且結果準確可靠。

5 結束語

模態密度，DLF，CDLF以及輸入功率是SEA方法中極其重要的參數。總體來說理論方法能夠解決某些簡單的實際問題，但對于復雜的汽車結構來說，結構過于簡化使理論值同實際測量值存在一定的偏差，造成結果不可信。筆者從實驗角度詳細地介紹了模態密度，DLF，CDLF以及輸入功率的測試方法，并依托于某國產車中高頻仿真分析，將實驗測得的SEA基本參數輸入到模型中，對簡化模型起到調整作用，并將實驗測試獲得的輸入功率作為激勵輸入到模型中，仿真計算出駕駛員右耳處的SPL。將仿真值與測試值相比較發現，其仿真值與測試值在中高頻范圍內吻合較好，這表明基于實驗SEA方法建立精確轎車模型預測車內噪聲的方法準確可靠，為準確預測車內噪聲提供了一種有效的方法。

[1] 盛美萍，王敏慶，孫進才.衰減法測定穩態振動系統損耗因子的實驗分析技術[J].西北工業大學學報，2001,19(1): 131-137.

Sheng Meiping, Wang Minqing, Sun Jincai. Experimental analysis on damping loss factor of steady vibration system using decay method [J]. Journal of Northwestern Polytechnical University, 2001,19(1): 131-137.(in Chinese)

[2] 宋繼強，王登峰，馬天飛,等.汽車車身復雜子結構模態密度確定方法[J].吉林大學學報：工學版，2009,39(2): 269-274.

Song Jiqiang, Wang Dengfeng, Ma Tianfei, et al. Calculation method of auto body complex sub-structure modal density [J]. Journal of Jilin University：Engineering and Technology Edition, 2009,39(2): 269-274. (in Chinese)

[3] 歐陽山，魯帆，伍先俊,等.列車白車身損耗因子試驗研究[J].振動與沖擊，2015, 34(5): 20-25.

Ouyang Shan, Lu Fan, Wu Xianjun, et al. Experimental study on loss factors for train carriage body in white[J]. Journal of Vibration and Shock, 2015, 34(5): 20-25. (in Chinese)

[4] 毛伯永，謝石林，張希農.沖擊載荷識別的瞬態統計能量分析方法[J].振動與沖擊，2013,32(14): 46-51.

Mao Boyong, Xie Shilin, Zhang Xinong. Identification of impact load based on transient statistical energy analysis method [J]. Journal of Vibration and Shock, 2013,32(14): 46-51.(in Chinese)

[5] 張強，郝志勇，毛杰,等.基于SEA的鎂質前圍板與車內聲場耦合優化分析[J].汽車工程，2014,36(8): 1004-1008.

Zhang Qiang, Hao Zhiyong, Mao Jie, et al. Coupling and optimization analysis of magnesium bulkhead and interior sound field based on SEA [J]. Automotive Engineering, 2014,36(8): 1004-1008.(in Chinese)

[6] 程廣利，朱石堅.統計能量分析法及其損耗因子確定方法綜述[J].船舶工程，2004, 26(4): 10-16.

Cheng Guangli, Zhu Shijian. Method review of statistical energy analysis and damping loss factor [J]. Shipping Engineering, 2004, 26(4): 10-16.(in Chinese)

[7] 鮑曉華，劉建，劉冰,等.基于統計能量分析的汽車發電機損耗因子的討論[J].電工技術學報，2011, 26(12): 49-55.

Bao Xiaohua, Liu Jian, Liu Bing, et al. Discussion for loss factors of automobile alternators based on statistical energy analysis [J].Journal of Electrical Engineering, 2011, 26(12): 49-55. (in Chinese)

[8] 孫進才.復雜結構的損耗因子和耦合損耗因子的測量方法[J].聲學學報，1995,20(2): 127-135.

Sun Jincai. Measuring method of dissipation and coupling loss factors for complex structures [J]. Journal of Acta Acoustica, 1995,20(2): 127-135.(in Chinese)

[9] 張紅亮，孔憲仁，劉源,等.寬頻域的內損耗因子實驗辨識方法研究[J].振動與沖擊，2013, 32(12): 179-185.

Zhang Hongliang, Kong Xianren, Liu Yuan, et al. Test identification of damping loss factor in a wider frequency range [J]. Journal of Vibration and Shock, 2013, 32(12): 179-185.(in Chinese)

[10] 方源，章桐，于蓬，等.電動車動力總成振動噪聲的試驗研究[J]. 振動、測試與診斷，2015, 35(2): 218-224.

Fang Yuan, Zhang Tong, Yu Peng, et al. Experimental study on vibration and noise of electric powertrain [J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 218-224.(in Chinese)

[11] Zhang Xiaoxuan, Wu Xingrang. Application research of statistical energy analysis on vehicle sound package [EB/OL]. ( 2012-11-07)[ 2015-08-31]． DOI:10.1007/978-3-642-33832-8_39.

[12] Cordioli J A, Triches J, Gerges S. et al, Applications of the statistic energy Analysis to vibro-acoustic modeling of vehicle [EB/OL]. (2004-11-16)[ 2015-08-31]．Doi:10.4271/2004-01-3352.

[13] 雷燁，盛美萍，肖和業.直升機艙內噪聲預估與分析[J].振動、測試與診斷，2010, 30(6): 617-620.

Lei Ye, Sheng Meiping, Xiao Heye. Prediction and analysis of helicopter cockpit noise [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 617-620.(in Chinese)

教育部創新團隊發展計劃資助項目(IRT3087)

2015-08-31；

2015-11-16

U491.9+1；TB535+.2；TH825

邢鵬，女，1984年10月生，博士生。主要研究方向為汽車車內噪聲仿真預測分析與試驗研究。曾發表《The subjective evaluation on sound quality for interior noise based on customer satisfaction》(《Computer Modeling and New Technologies》2014,Vol.18,No.12)等論文。

E-mail:xingpeng0634@126.com