Cn-內射模及其刻畫

王 茜, 王芳貴, 何 可

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

Cn-內射模及其刻畫

王 茜, 王芳貴*, 何 可

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

n-余撓模; Cn-內射模; Artin半單環; CnI-遺傳環

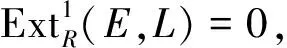
1959年,D. K. Harrison[5]為了刻畫非有限的Abelian群的結構性質,開展了余撓模的研究(如文獻[6-7]).左R-模C稱為余撓模,是指對一切平坦模F,都有

2006年,Mao L. X.等[8]引入了n-余撓模概念,左R-模C稱為n-余撓模,是指對一切平坦模F,都有

本文借助n-余撓模類引入了Cn-內射模的概念,并討論其相關性質和等價刻畫,證明了L是內射模當且僅當L是n-余撓維數不超過1的Cn-內射模.借助于Cn-內射模的概念,給出了Artin半單環和弱整體維數不超過n的環的新刻畫.證明了每個R模都是Cn-內射模的環就是Artin半單環,每個n-余撓模是Cn-內射模的環就是弱整體維數不超過n的環;從而有每個余撓模是C-內射模的環就是von Neumann正則環,1-余撓模是C1-內射模的整環就是Prüfer整環.最后用Cn-內射模的商模是Cn-內射模定義了CnI-遺傳環并得出了其等價刻畫和一些性質,即R是CnI-遺傳環當且僅當R上每個n-余撓模的投射維數不超過1.

以下恒設R是有單位元的結合環,n是非負整數,模指左模.用F、P和I分別表示平坦模類、投射模類和內射模類,Fn和Cn分別表示平坦維數不超過n的模類和n-余撓模類.另外,pdRM與idRM分別表示R-模M的投射維數和內射維數,w.gl.dim(R)表示環R的弱整體維數,其他涉及到的符號可以在文獻[14]中找到.

1 Cn-內射模定義和基本性質

注1.2下面的事實是顯然的.

1) 內射模是Cn-內射模.

2) 若m≥n≥0,則CnI?CmI,即Cn-內射模是Cm-內射模.

3) 由于I?Cn,故CnI?CPI,即Cn-內射模是余純內射模.

證明由自然同構

即得.

命題1.4設0→X→Y→Z→0是正合列.若X、Z是Cn-內射模,則Y也是Cn-內射模.

設L是一個模類.設M∈L,X是R-模,φ:M→X是同態.若對任何N∈L,以及任何同態g:N→X,恒有同態h:N→M,使下圖

完備為交換圖,則(M,φ)稱為X的L-預蓋.顯然,φ:M→X是L-預蓋當且僅當對任何N∈L,誘導同態

φ*:HomR(N,M)→HomR(N,X)

是滿同態.

定理1.5對R-模L，以下各條等價:

1)L是Cn-內射模;

2) 若ξ:0→L→C→Z→0是正合列,其中C∈Cn,則C→Z是Z的Cn-預蓋;

3)L是某個Cn-滿預蓋φ:A→B的核,其中A是內射模;

4) 若ξ:0→A→B→C→0是正合列,其中C∈Cn,則HomR(ξ,L)也是正合列;

2)?3)L能嵌入內射模E,注意E∈Cn.取A=E,B=E/L.由條件,L是Cn-滿預蓋φ:A→B的核.

設R是環,M是R-模.若M有如下形式的n-余撓分解0→M→C0→C1→…→Cm-1→Cm→0,其中C0,C1,…,Cm是n-余撓模,則稱M的n-余撓維數不超過m,記為cndRM.自然地,M的n-余撓維數cndRM就是M的n-余撓分解的最短長度.當M沒有上述形式的n-余撓分解時,則記cndRM=∞.對環R,記

Cn.D(R)=sup{cndRM|?M∈RM},

稱為R的n-余撓整體維數.關于模與環的n-余撓維數的討論,n=0的情形參見文獻[15],一般情形參見文獻[10].

定理1.6設L是R-模,則L是內射模當且僅當L是Cn-內射模,且cndRL≤1.

證明若L是內射模,顯然有L是Cn-內射模,且cndRL≤1.反之,考慮正合列0→L→E→C→0,其中E是內射模.由條件有cndRC=0,即C是n-余撓模.由文獻[16]的推論7.20,此正合列分裂,因此有L是內射模.

回顧環R稱為Cn-遺傳環,是指每個n-余撓模的商模是n-余撓模,等價于說Cn.D(R)≤1(參見文獻[10]).稱環R是完全環當且僅當所有R-模是余撓模(參見文獻[17]),由定理1.6,可得如下推論.

推論1.7設R是Cn-遺傳環,L是R-模,則L是內射模當且僅當L是Cn-內射模.

推論1.8設R是完全環,L是R-模,則L是內射模當且僅當L是C-內射模.

2 環的刻畫

下面利用Cn-內射模來刻畫環,首先討論環的半單性,即環R上每個模都是Cn-內射模時,R所具備的一些性質.

定理2.1對環R,以下各條等價:

1) 對任何n≥0,有RM=CnI,即每個R-模是Cn-內射模;

2) 對任何n≥0,有Cn?P,即每個n-余撓模是投射模;

3) 存在n≥0,使得RM=CnI,即每個R-模是Cn-內射模;

4) 存在n≥0,使得Cn?P,即每個n-余撓模是投射模;

5)R是Artin半單環;

6) 每個余撓模是投射模;

7) 對任何n≥0,有Cn=P;

8) 存在n≥0,使得Cn=P.

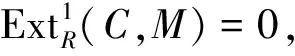
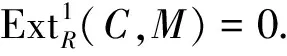
3)?4) 類似于1)?2).

1)?3) 顯然.

4)?5) 見文獻[9]的推論6.5.

5)?6) 顯然,因為半單環每個模都是投射模.

6)?2) 由對任何n≥0,n-余撓模都是余撓模即得.

1)?7)?8)?1) 顯然.

下面通過n-余撓模與Cn-內射模的關系來刻畫環的性質.

定理2.2設n是非負整數.對環R,以下各條等價:

1)w.gl.dim(R)≤n;

2) Cn?CnI,即每個n-余撓模是Cn-內射模;

4) 對任何C,M∈Cn,及任何k≥1,有

5) 若cndRX<∞,則對任何M∈Cn有

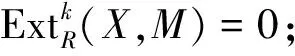
7) Cn?Fn,即n-余撓模的平坦維數不超過n.

證明1)?2) 由文獻[9]的定理6.4,w.gl.dim(R)≤n當且僅當每個n-余撓模是內射模,從而有Cn?CnI.

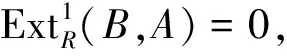
w.gl.dim(R)≤n.

2)?3)和2)?4)?3) 顯然.

4)?6) 設0→X→C0→C1→…→Cs→0是正合列,其中C0,C1,…,Cs是n-余撓模.由假設,對任何i≥0,及k>0,有

故

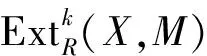
6)?5)?3) 顯然.

3)?7) 由(Fn,Cn)是余撓理論即得.

目前已有許多刻畫von Neumann正則環和Prüfer整環的方法,也得到諸多結果.借助Cn-內射模的概念,在定理2.2中的分別取n=0和n=1,得到下面關于von Neumann正則環和Prüfer整環的新刻畫.

推論2.3對環R,以下各條等價:

1)R是von Neumann正則環;

2) 余撓模是C-內射模;

3) 對任何C,M∈C,有

4) 對任何C,M∈C,及任何k≥1,有

5) 若cdRX<∞,則對任何M∈C,有

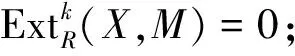
7) C?F,即余撓模是平坦模.

推論2.4對整環R,以下各條等價:

1)R是Prüfer整環;

2) 1-余撓模是C1-內射模;

4) 對任何C,M∈C1,及任何k≥1,有

5) 若cdRX<∞,則對任何M∈C1,有

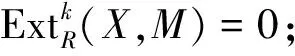
7)C1?F1,即1-余撓模的平坦維數不超過1.

對于遺傳環的研究已經很普遍,眾所周知,可以用內射模的商模是內射模來刻畫遺傳環;類似的,也可以用Cn-內射模來定義一類廣義的遺傳環.

定義2.5若Cn-內射模的商模還是Cn-內射模,則稱R為CnI-遺傳環,C0I-遺傳環簡稱CI-遺傳環.

注2.61) 若m≥n≥0,則CnI-遺傳環是CmI-遺傳環;

2) 對任何n,Artin半單環是CnI-遺傳環;

3) 由定理1.6易知R是遺傳環當且僅當R是CnI-遺傳環且R是Cn-遺傳環.

定理2.7對環R,以下各條等價:

1)R是CnI-遺傳環;

2) 內射模的商模是Cn-內射模;

3) 每個n-余撓模的投射維數不超過1.

證明1)?2) 由內射模是Cn-內射模顯然.

推論2.8若R是CnI-遺傳環且每個Cn-內射模是內射模,則R是遺傳環.

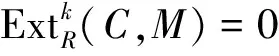
推論2.10對任意的n,Noether的CnI-遺傳環是1-Gorenstein環.

證明由定理2.7知R是CnI-遺傳環當且僅當n-余撓模的投射維數不超過1,又內射模是n-余撓模,所以內射模的投射維數不超過1,從而R是1-Gorenstein環(詳見文獻[18]的定理9.1.11).

[1] ENOCHS E E, JENDA O M G. Copure injective modules[J]. Quaestiones Math,1991,14(14):401-409.

[2] MAO L X, DING N Q. Relative copure injective and copure flat modules[J]. Pure and Applied Algebra,2007,208(2):635-646.

[3] ENOCHS E, JENDA O M G. Copure injective resolusions, flat resolvents and dimensions[J]. Comment Math Univ Carolin,1993,34(2):203-211.

[4] DING N Q, CHEN J L. On copure flat modules and flat resolvents[J]. Commun Algebra,1996,24(3):1071-1081.

[5] HARRISON D K. Infinite abelian groups and homological methods[J]. Ann Math,1959,69(2):366-391.

[6] MAO L X, DING N Q. Notes on cotorsion modules[J]. Commun Algebra,2005,33(1):349-360.

[7] MAO L X, DING N Q. Cotorsion modules and relative pure-injectivity[J]. J Australian Math Soc,2006,81(2):225-244.

[8] MAO L X, DING N Q. Relative cotorsion modules and relative flat modules[J]. Commun Algebra,2006,34(6):2303-2317.

[9] MAO L X, DING N Q. Envelopes and covers by modules of finite FP-injective and flat dimensions[J]. Commun Algebra,2007,35(3):833-849.

[10] 熊濤. 模類Fn確定的同調理論及其應用[D]. 成都:四川師范大學,2016.

[11] ENOCHS E E, HUANG Z Y. Injective envelopes and (gorenstein) flat covers[J]. Algebra Represent Theory,2012,15(6):1131-1145.

[12] 任偉,劉仲奎. 余撓模與n-余撓模[D]. 蘭州:西北師范大學,2009.

[13] 任偉. 關于cotorsion模與n-cotorsion模[J]. 甘肅科學學報,2008,20(4):33-36.

[14] 王芳貴. 交換環與星型算子理論[M]. 北京:科學出版社,2006.

[15] MAO L X, DING N Q. The cotorsion dimension of modules and rings[J]. Abelian Groups Rings Modules & Homological Algebra,2006,249:217-233.

[16] ROTMAN J J. An Introduction to Homological Algebra[M]. London:Academic Press,1979.

[17] XU J Z. Flat cover of modules[C]//Lecture Notes of Math,1634. Berlin:Springer-Verlag,1996.

[18] ENOCHS E E, JENDA O M G. Relative Homological Algebra[M]. Berlin:Walter de Gruyter,2000.

[19] 徐龍玉,王芳貴,陳翰林.P-投射模的刻畫[J]. 四川師范大學學報(自然科學版),2013,36(4):500-503.

[20] 熊濤,王芳貴,胡葵. 余純投射模與CPH環[J]. 四川師范大學學報(自然科學版),2013,36(2):198-201.

[21] 謝晉,王芳貴,熊濤. Pn-內射模及其刻畫[J]. 四川師范大學學報(自然科學版),2016,39(2):159-162.

[22] 朱占敏. 一類廣義遺傳環[J]. 純粹數學與應用數學,2003,19(1):68-71.

[23] IWANAYA Y. On rings with finite self-injective dimension[J]. Tsukuba J Math,1980,4(1):107-113.

[24] G?BEL R, TRLIFAJ J. Approximations and Endomorphism Algebras of Modules[M]. New York:Walter de Gruyter,2006.

The Characterization on Cn-injective Modules

WANG Xi, WANG Fanggui, HE Ke

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

n-cotorsion module; Cn-injective module; Artin semisimple rings; CnI-hereditary ring

2016-11-08

國家自然科學基金(11671283)和教育部博士點專項科研基金(20125134110002)

*通信作者簡介:王芳貴(1955—),男,教授,主要從事交換代數、同調代數與代數K-理論的研究,E-mail:wangfg2004@163.com

O154

A

1001-8395(2017)05-0588-05

10.3969/j.issn.1001-8395.2017.05.004

2010MSC:16D50; 16E10; 16E30

(編輯 余 毅)