一類廣義KdV方程的行波解

王小嬌, 謝瑩瑩, 汪大召, 朱世輝

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

一類廣義KdV方程的行波解

王小嬌, 謝瑩瑩, 汪大召, 朱世輝*

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

研究一類廣義KdV方程,包含了經典的KdV方程、mKdV方程和Camassa-Holm方程,并利用tanh函數方法,得到了此類廣義KdV方程的新行波解.

tanh函數方法; 廣義KdV方程; 行波解

非線性發展方程作為描述復雜物理現象的數學模型,其研究涉及數學、物理、生物、工程等現代科學中各個領域,而方程的精確解又使得物理現象得到進一步的科學解釋,因此,對數學家、物理學家、工程學家及應用科學工作者來說,尋找對應實用背景方程的精確解一直是大家關注的問題.為了尋找非線性發展方程的精確解,專家學者已發現了許多求解方法,例如painleve截尾展開法[1]、齊次平衡方法[2]、雙曲函數法[3]、sine-cosine方法[4]、Jacobi橢圓函數展開法[5],以及作為Jacobi橢圓函數展開法一般化的F-展開法[6]、改進的展開法[7],利用這些方法得到非線性發展方程中許多豐富的精確解.

本文運用tanh函數方法,研究了如下廣義非線性KdV方程

ut+(aun-bu2n)ux+λutxx+

[uk(um)xx]x=0,

(1)

其中,a、b、λ是常數.顯然,當n=1,a≠0,b=0,λ=0,k=0,m=1時,方程(1)即為著名的KdV方程,它描述了在重力的影響下,波在淺水表面單向自由傳播的過程,其中u(x,t)為傳播過程中波的高度,x為傳播方向上波的相對位置比例,t為相對時間比例.與這個方程類似,當n=1,a=0,b≠0,λ=0,k=0,m=1時,方程(1)變為mKdV方程.當λ=0,k=0,m=1時,方程(1)變為廣義KdV方程.以上這些方程具有一定的物理意義,許多學者對它們進行了深入的研究,如文獻[8]討論了KdV方程的可積性,并說明了此方程是可積的.文獻[9]指出mKdV方程是描述弱色散現象的近似模型,并研究了方程的孤波解、代數解等.

當n=1,a=3,b=0,λ=-α,k=m=1時,方程變為Camassa-Holm方程,它主要描述由于引力影響,該波在淺水表面上的單向傳播現象,其中u(x,t)表示在t≥0時,波在x方向上的傳播速度.多年來,此方程得到了廣泛關注,并對此方程的解構造進行了大量研究,獲得了很多結果.文獻[10]論述了此方程的原始起源,文獻[11-12]論述了此方程新的起源,文獻[10,13]討論了此方程的可積性,說明了此方程是完全可積的,文獻[14-15]獲得了此方程豐富的較全面的精確解,文獻[16-17]通過不同方法得到了C-H方程的顯示行波解.另外,不難發現,當n=1,a=4,b=0,λ=-1,k=m=1時,方程為Degasperis-Procesi方程.此方程的精確解問題也已經有大量的研究[18-19],其中,文獻[19]用色散方法得出了該方程的尖孤波解.

本文獲得了方程(1)在m、k取不同值時對應方程的新行波解,大大豐富了此方程的解系,為專家學者在某些問題研究上提供了幫助.

1 方法介紹

這里先描述一下tanh函數方法的一般過程,以如下偏微分方程為例

p(u,ux,ut,uxx,uxxx,…)=0,

(2)

p是關于u,ux,ut,uxx,uxxx,…的多項式.

引入變換

u(x,t)=u(ξ),ξ=x-ct.

(3)

將(3)式代入(2)式,得到一個關于u(ξ)的常微分方程

p(u,uξ,uξξ,uξξξ,…)=0.

(4)

引進一個新的變量

Y=tanh(μξ),ξ=x-ct,

(5)

得到

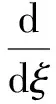
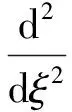
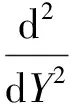
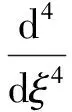
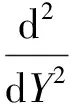
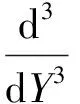
(6)

應用以下級數展開

(7)

其中,ak是待定常數(k=0,1,2,…,M),M通過平衡給定方程(4)中的最高階導數項和非線性項來確定,將(6)和(7)式代入(4)式中,那么常微分方程(4)的左邊可化為關于Y的多項式,合并Y的相同冪次,令每一項的系數為零,得到一個關于ak(k=0,1,2,…,M)和μ、c的代數方程組,利用代入消元法求解這個方程組,將這些結果代入(7)式,得到偏微分方程(2)含有多個參數的行波解的一般形式.

2 應用

引入如下行波變換

u(x,t)=u(ξ),ξ=x-ct.

(8)

將(8)式代入(1)式得到

cλuξξξ+[uk(um)ξξ]ξ=0.

(9)

積分(9)式得

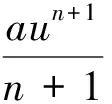
cλu″+uk(um)″=0.

(10)

平衡(10)式中的uk(um)與u2n+1得到

(2n+1)M=kM+mM+2,

(11)

所以

當方程(1)中m、k取不同值時,尋求對應方程的行波解,分以下幾種情況來討論.

情況2.1當m=k=0時,方程變為

ut+(aun-bu2n)ux+λutxx=0.

(12)

此時

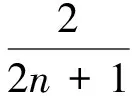
(13)

令

u=v1/n,

(14)

將(14)式及m=k=0代入(10)式得到

-cn2(2n+1)(n+1)v2+an2(2n+1)v3-

bn2(n+1)v4-cλn(n+1)(2n+1)vv″+

cλ(n2-1)(2n+1)(v′)2=0.

(15)

平衡v4、vv″得到M=1,假設(15)式具有如下形式解

v(ξ)=a0+a1Y.

(16)

將(16)式代入(15)式合并Y的相同冪次,并令每一項系數為零,得到關于a0、a1、c、μ、a、b、n的一個代數方程組:

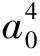
-2cn2(2n+1)(n+1)+3an2(2n+1)a0-

-cn2(2n+1)(n+1)+3an2(2n+1)a0-

2cλ(n2-1)(2n+1)μ2=0,

2cλn(2n+1)(n+1)a0μ2=0,

cλ(n2-1)(2n+1)μ2=0.

(17)

利用代入消元法求解方程組(17)得到:

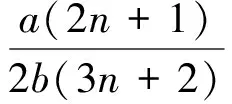
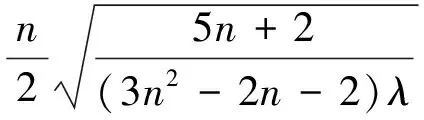
(18)

于是

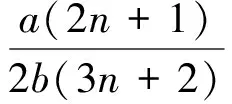
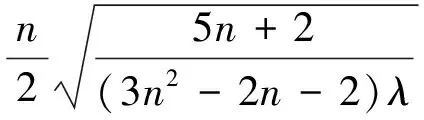
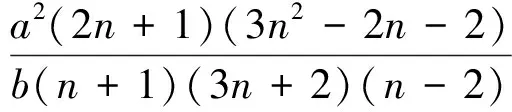
(19)

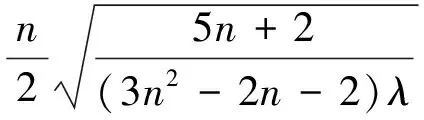
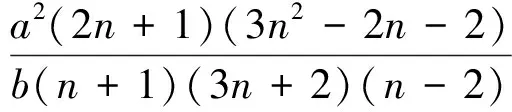
(20)

由(14)式得到廣義KdV方程精確解行波解如下:

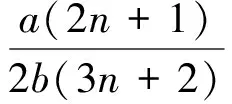
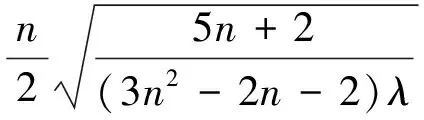
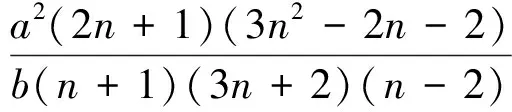
(21)

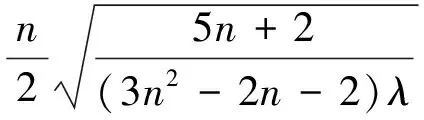
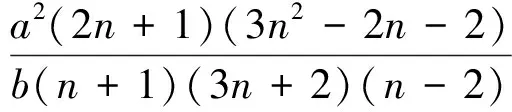
(22)

情況2.2當m=0,k=1時,方程變為

ut+(aun-bu2n)ux+λutxx=0.

(23)

此方程完全與情況2.1相同,所以對應的解為:

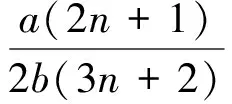
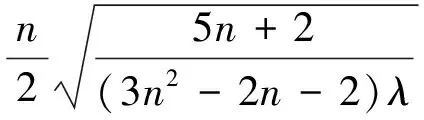
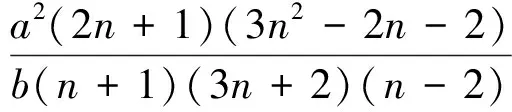
(24)

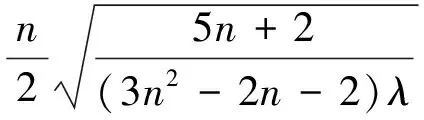
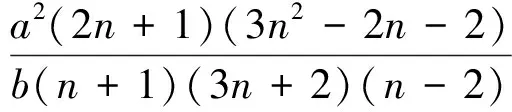
(25)

實際上,當m=0,k取任意值時,方程(1)都變為

ut+(aun-bu2n)ux+λutxx=0.

(26)

所以,當m=0,k取任意值時,方程的解都為:

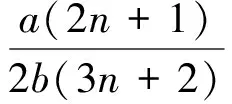
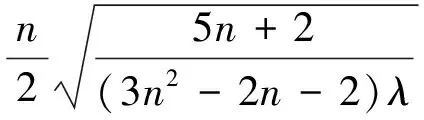
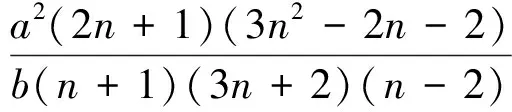
(27)

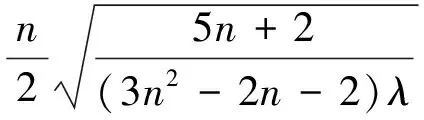
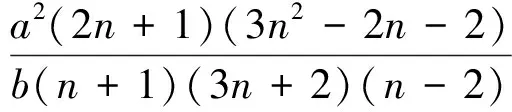
(28)

情況2.3當m=1,k=0時,方程變為

ut+(aun-bu2n)ux+λutxx+uxxx=0.

(29)

此時

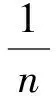
(30)

令

u=v1/n,

(31)

將(31)式及m=1,k=0代入(10)式可得

(1-c)n2(n+1)v2(2n+1)+

an2(2n+1)v3-bn2(n+1)v4+

(1-cλ)n(n+1)(2n+1)vv″+

(1-cλ)(n2-1)(2n+1)(v′)2=0.

(32)

平衡v4和vv″得到M=1,假設(32)式具有如下形式解

v(ξ)=a0+a1Y.

(33)

將(33)式代入(32)式合并Y的相同冪次,并令每一項系數為零,得到關于a0、a1、c、μ、a、b、n的一個代數方程組:

-2cn2(2n+1)(n+1)+

2(1-cλ)n(2n+1)(n+1)μ2=0,

-cn2(2n+1)(n+1)+3an2(2n+1)a0-

2(1-cλ)(n2-1)(2n+1)μ2=0,

2(1-cλ)n(2n+1)(n+1)a0μ2=0,

(1-cλ)(1-n2)(2n+1)μ2=0.

(34)

利用代入消元法求解方程組(34)得到:

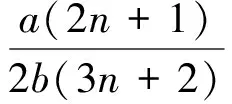
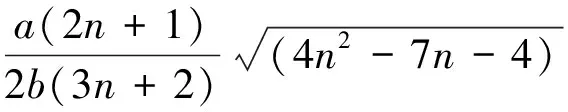
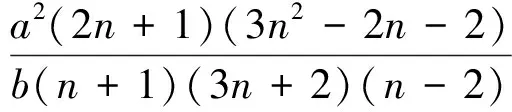
μ=±a{[2(2n+1)(3n2-2n-2)+

3n2(2n+1)2(n-2)]/[4b(n+1)×

(3n+2)2(n-2)+a(2n+1)×

(3n2-2n-2)λ]}1/2,

(35)

于是

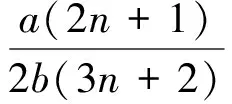
tanh(a{[2(2n+1)(3n2-2n-2)+

3n2(2n+1)2(n-2)]/[4b(n+1)×

(3n+2)2(n-2)+a(2n+1)×

(3n2-2n-2)λ]}1/2×

(36)

coth(a{[2(2n+1)(3n2-2n-2)+

3n2(2n+1)2(n-2)]/[4b(n+1)(3n+2)2×

(n-2)+a(2n+1)(3n2-2n-2)λ]}1/2×

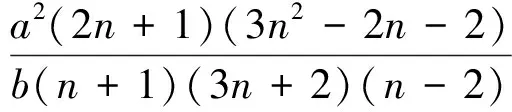
(37)

由(31)式得到廣義KdV方程精確解行波解如下:

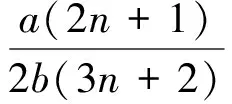
tanh(a{[2(2n+1)(3n2-2n-2)+

3n2(2n+1)2(n-2)]/[4b(n+1)(3n+2)2×

(n-2)+a(2n+1)(3n2-2n-2)λ]}1/2×

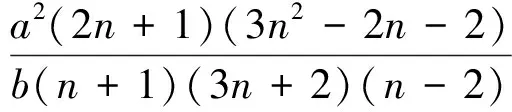
(38)

coth(a{[2(2n+1)(3n2-2n-2)+

3n2(2n+1)2(n-2)]/[4b(n+1)(3n+2)2×

(n-2)+a(2n+1)(3n2-2n-2)λ]}1/2×

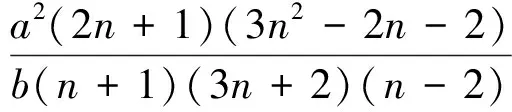
(39)

情況2.4當m=1/2,k=1/2時,方程變為

ut+(aun-bu2n)ux+

λutxx+[u1/2(u1/2)xx]x=0.

(40)

令

u=v1/n,

(41)

將(41)式及m=1/2,k=1/2代入(10)式可得

-4cn2(n+1)v2(2n+1)+

4an2(2n+1)v3-4bn2(n+1)v4+

2n(n+1)(2n+1)(1-2cλ)vv″+

(1+n)(2n+1)[(1-2n)-

4cλ(1-n)](v′)2=0.

(42)

平衡v4和vv″得到M=1,假設(42)式具有如下形式解

v(ξ)=a0+a1Y.

(43)

將(43)式代入(42)式合并Y的相同冪次,并令每一項系數為零,得到關于a0、a1、c、μ、a、b、n的一個代數方程組:

-2cn2(2n+1)(n+1)+

(n+1)(2n+1)(1-2cλ)μ2=0,

-2cn2(2n+1)(n+1)+

(1+n)(2n+1)[(1-2n)-4cλ(1-n)]μ2-

2n(n+1)(2n+1)(1-2cλ)μ2=0,

(n+1)(2n+1)(1-2cλ))a0μ2=0,

(2n+1)[(1-2n)-4cλ(1-n)]μ2+

2n(2n+1)(1-2cλ)μ2=0.

(44)

利用代入消元法求解方程組(44)得到:

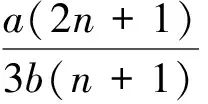
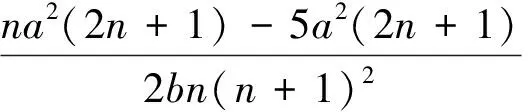
μ=±{[5bn2(n+1)+

b(1-2n)(n+1)]/[(2n+1)(n-5)-

12a2(2n+1)(1-n)λ]}1/2,

(45)

于是

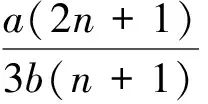
tanh({[5bn2(n+1)+

b(1-2n)(n+1)]/[(2n+1)(n-5)-

12a2(2n+1)(1-n)λ]}1/2[x-

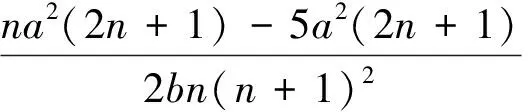
(46)

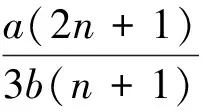
coth({[5bn2(n+1)+

b(1-2n)(n+1)]/[(2n+1)(n-5)-

12a2(2n+1)(1-n)λ]}1/2×

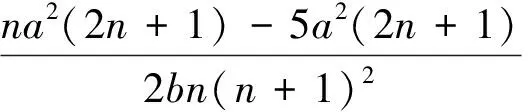
(47)

由(41)式得到廣義KdV方程精確解行波解如下:

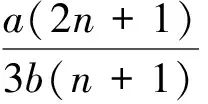
tanh({[5bn2(n+1)+

b(1-2n)(n+1)]/[(2n+1)(n-5)-

12a2(2n+1)(1-n)λ]}1/2[x-

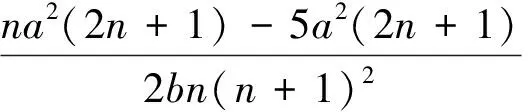
(48)

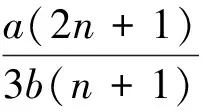
coth({[5bn2(n+1)+

b(1-2n)(n+1)]/[(2n+1)(n-5)-

12a2(2n+1)(1-n)λ]}1/2[x-

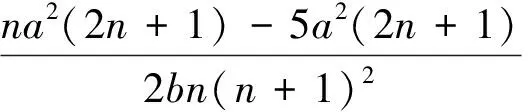
(49)

3 結束語

本文把tanh函數方法應用于廣義KdV方程,成功獲得了廣義KdV方程一系列的含多個參數的精確行波解,這些精確解豐富了廣義KdV方程精確解的解系,有助于物理上對方程的研究.

[1] 張解放,陳芳躍. 截斷展開法和廣義變系數KdV方程[J]. 物理學報,2001,50(9):1648-1650.

[2] WANG M L, ZHOU Y B, LI Z B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys Lett,1996,A216(1):67-75.

[3] 郭冠平,張解放. 關于雙曲函數方法求孤波解的注記[J]. 物理學報,2002,51(6):1159-1162.

[4] YAN C T. A simple transformation for nonlinear waves[J]. Phys Lett,1996,A224(1/2):77-84.

[5] 向以華,石義霞. (2+1)維色散長波方程的擴展橢圓函數有理展開解法[J]. 數學雜志,2009,29(2):206-210.

[6] 曹瑞. 改進的F-展開方法和耦合Klein-Gordon方程的精確解[J]. 蘭州大學學報(自然科學版),2007,43(6):112-116.

[7] 曹瑞. 一類廣義Zakharov方程的精確行波解[J]. 數學雜志,2013,33(5):837-843.

[8] MCKEAN H P. Integrable Sustems and Algebraic Curves Global Analysis Lecture Notes in Matheatics[M]. Berlin:Springer-Verlag,1979:83-200.

[9] PELINOVSKY D, GRIMSHAW R. An asymptotic approach to solitary wave inatability and critical collapse in long-wave KdV-type evolution equations[J]. Physcia,1996,D98(1):139-155.

[10] CAMASSA R, HOLM D. An integrable shallow water equation with peaked solitions[J]. Phys Rev Lett,1993,71(11):1661-1664.

[11] DULLIN H R, GOTTWALD G A, HOLM D D. An integrable shallow water equation with linear and nonlinear dispersion[J]. Phys Rev Lett,2001,87(19):4501-4504.

[12] JOHNSON R S. Camassa-Holm equation Korteweg-de Vries and related models for water waves[J]. Fluid Mech,2002,457(455):63-82.

[13] BEALS R, SATTINGER D, SZMIGIELSKI J. Acoustic scattering and the extended Korteweg-de Vries hierarchy[J]. Adv Math,1998,140(2):190-206.

[14] ANN I. Global existence of solutions and breaking wave for shallow wave equations:a geometric approath[J]. Fourier(Grenoble),2000,50(2):321-362.

[15] CONSTANTIN A, ESCHER J. Global existence and blow-up for a shallow water equation[J]. Ann Scuola Norm Sup Pisa,1988,26(2):303-328.

[16] LIU Z R, QIAN T F. Peakons and their bifurcation in a generalized Camassa-Holm equation[J]. Int J Bifurcation Chaos,2001,11(3):781-792.

[17] LIU Z R, QIAN T F. Peakons of the Camassa-Holm equation[J]. Appl Math Model,2002,26(3):473-480.

[18] VAKHNENKO V O, PARKES E J. Periodic and solitary-wave solutions of the Degasperis-Procesi equation[J]. Chaos Solitons and Fractals,2004,20(5):1059-1073.

[19] LUNDMARK H, SZMIGIELSKI J. Multi-peakon solutions of the Degasperis-Procesi equation[J]. Inverse Problems,2003,19(6):1241-1245.

[20] DOOLEY A L. More on ocean rogues[J]. Society of Maritime Arbitrators Inc,2006,38(1):13-15.

[21] OSBORNE A R. The random and deterministic dynamics of “rogue waves” in unidirectional deep-water wave trains[J]. Marine Structures,2001,14(3):275-293.

[22] OSBORNE A R, MIGUEL O, MARINA S. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains[J]. Phys Lett,2000,A275(5/6):386-393.

[23] WANG M L. Solitary wave solutions for variant Boussinesq equaions[J]. Phys Lett,1995,A199:169-172.

[24] WANG Y Y, HE J S, LI Y S. Soliton and rogue wave solution of the new nonau-tonomous nonlinear Schr?dinger equation[J]. Commun Theory Phys,2011,56(6):995-1004.

[25] YAN Z Y. Nonautonomous “rogue” in the inhomogeneous nonlinear Schr?dinger equation with variable coefficients[J]. Phys Lett,2010,A374(4):672-679.

Travelling Wave Solution of the Generalized KdV Equation

WANG Xiaojiao, XIE Yingying, WANG Dazhao, ZHU Shihui

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

In this paper, we study a class of generalized KdV equations including the classical KdV equation, mKdV equation and Camassa-Holm equation. By using tanh function method, we obtain some new travelling wave solutions of the generalized KdV equation.

generalized KdV equation; tanh function method; travelling wave solution

2016-09-02

國家自然科學基金(11501395)和四川省杰出青年基金(2014JQ0039)

*通信作者簡介：朱世輝(1983—),男,副教授,主要從事非線性方程爆破解動力學性質的研究,E-mail:shihuizhumath@163.com

O175.29

A

1001-8395(2017)05-0600-06

10.3969/j.issn.1001-8395.2017.05.006

2010MSC：35C07; 35Q40

(編輯 李德華)