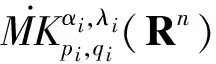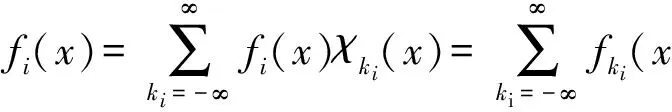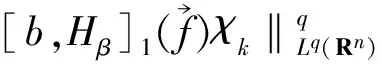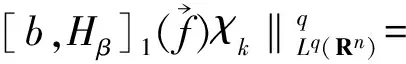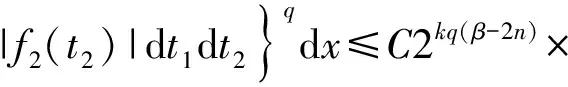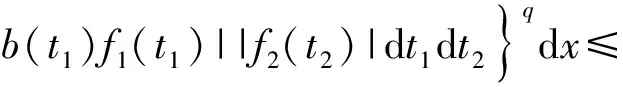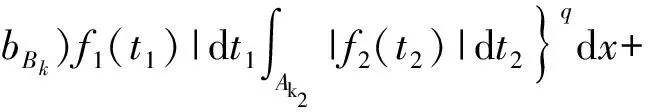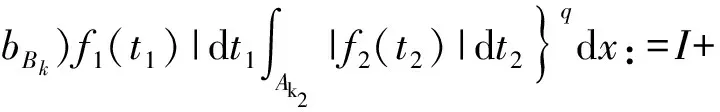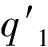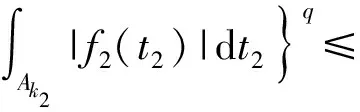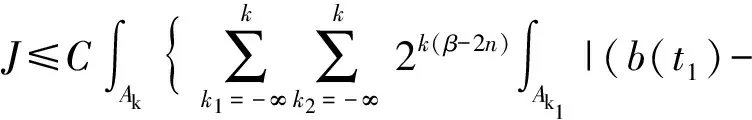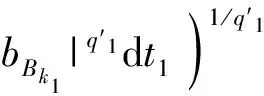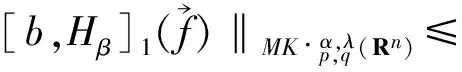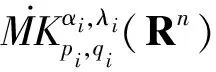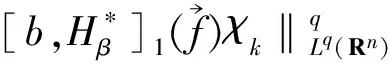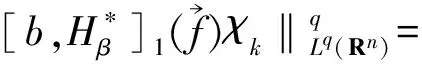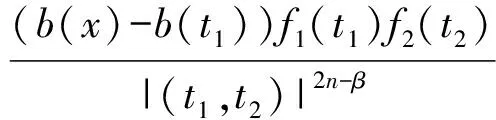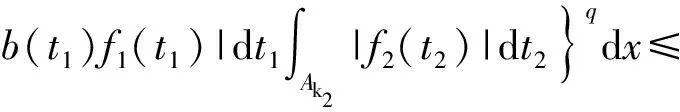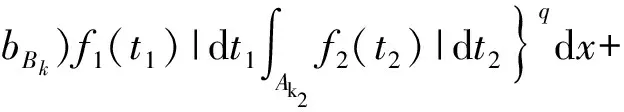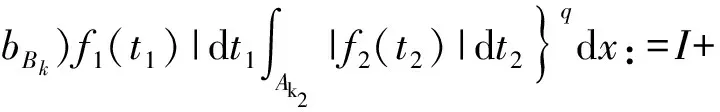雙線性分數次Hardy算子交換子在Herz-Morrey空間上的估計
劉榮輝, 周 疆
(新疆大學 數學與系統科學學院, 烏魯木齊 新疆 830046)
雙線性分數次Hardy算子交換子在Herz-Morrey空間上的估計
劉榮輝, 周 疆*
(新疆大學 數學與系統科學學院, 烏魯木齊 新疆 830046)
證明了雙線性分數次Hardy算子和雙線性分數次共軛Hardy算子分別與中心BMO函數生成的交換子在Herz-Morrey空間上的有界性,同時得到了雙線性Hardy算子交換子和雙線性共軛Hardy算子的相應結果.
1 預備知識
雙線性算子的研究起源于20世紀70年代,文獻[1-2]發現Calderón-Zygmund交換子的研究可以歸結為一類雙線性奇異積分算子的研究.隨后雙線性算子的有界性問題得到眾多研究者的關注,如文獻[3-6]等在此方面有非常出色的工作.與此同時,關于Hardy算子的研究也得到了迅速的發展,參見文獻[7-10].
1920年,Hardy在證明Hilbert雙重級數定理的過程中得到了Hardy積分不等式,此后Hardy算子的研究便引起了眾多學者的廣泛關注,他們不僅研究了Hardy積分不等式的各種不同形式的證明,而且還對其進行了推廣和應用[11-12].
1995年,M. Chirst等[13]給出了n維Hardy算子
2007年,傅尊偉等[14]首次給出了n維分數次Hardy算子
并建立了它們在Lebesgue 空間和齊次Herz 空間中的有界性,同時研究了與(中心BMO 空間) 函數所生成的交換子的有界性,其中,0≤β 首先介紹n維雙線性分數次Hardy算子的定義. 下面給出Herz-Morrey空間的定義.設Bk={x∈Rn:|x|≤2k}對于k∈Z,記Ak=BkBk-1且χk=χAk,其中χAk是Ak的特征函數. 其中 注1.2中心BMO空間被認為是BMO空間中的球心在原點時的BMO空間,但事實上,中心BMO空間不是BMO空間的一種簡單形式,比如中心BMO空間不滿足John-Nirenberg不等式,且 BMO(Rn), 在2003年,C.Pérez等[11]研究了如下定義的雙線性Calderón-Zygmund算子交換子: [T,b]1(f,g)=T(bf,g)-bT(f,g), [T,b]2(f,g)=T(f,bg)-bT(f,g), C.Pérez等[11]討論了交換子[T,b]i(i=1,2)在Lebesgue空間上的有界性,即如果b∈BMO(Rn),1 ‖[T,b]1(f,g)‖Lp(Rn),‖[T,b]2(f,g)‖Lp(Rn)≤ C‖b‖BMO(Rn)‖f‖Lp1(Rn)‖g‖Lp2(Rn), 同時也研究了當1/2 受上述工作的啟發,首先給出雙線性分數次Hardy算子交換子和雙線性分數次共軛Hardy算子交換子的定義. 本文是齊次Herz-Morrey空間上的結果,但是對于非齊次的Herz-Morrey空間同樣成立,文中的C通常表示與空間維數等有關的常數,每次出現時有可能其值并不相同,對于Rn中的可測子集E,用|E|表示E的Lebesgue測度. 定理2.1設0 定理2.2設0 令 0≤β<2n/max(q1,q2), α=α1+α2,λ=λ1+λ2, 則有: 在定理2.1中令β=0,有如下推論. 推論2.1設0 在定理2.2中令β=0,有如下推論. 引理3.1[14]設b∈CMO1(Rn)且i,k∈Z,則 |b(t)-bBk|≤|b(t)-bBi|+ C|i-k|‖b‖CMO1(Rn). 引理3.2設0<β ‖Iβf‖Lq2(Rn)≤C‖f‖Lq1(Rn). 令1/u=1/q1+1/q2,則1/q=1/u-β/n.注意到 χBj(x)≤C2-jβIβ(χBj)(x), 使用H?lder不等式得 ‖χk‖Lq(Rn)≤‖χBk‖Lq(Rn)≤C2-kβ‖Iβ(χBk)‖Lq(Rn)≤C2-kβ‖χBk‖Lu(Rn)≤C2-kβ‖χBk‖Lq1(Rn)‖χBk‖Lq2(Rn). 利用上式可得 下面估計J,由引理2.1可得 對于J1,通過H?lder不等式,類似于I的估計得 對于J2,由H?lder不等式,類似于I的估計有 J2≤C‖ 基于對I、I1和I2的估計可得 因為 定理2.1(ii)的證明與定理2.1(i)的證明類似,只是將交換子與函數f2結合,因此省略證明的細節. 現在分別估計I和J,對于I,由H?lder不等式 以及條件 可得 對于J,由引理2.1得 下面分別估計J1和J2.對于J1,由H?lder不等式類似I的估計得 對于J2,由H?lder不等式類似估計有 J2≤C‖ 結合I、J1和J2的估計可得 令1/p1+1/p2=1/γ,則1/γ-β/n=1/p,從而p>γ利用H?lder不等式和α=α1+α2,可得 S≤C‖ 所以,利用條件αi>λi+β/2-n/qi(i=1,2) 定理2.2(ii)的證明與定理2.2(i)的證明類似,因此不再贅言. [1] COIFMAN R R, MEYER Y. On commutators of singular integrals and bilinear singular integrals[J]. Trans Am Math Soc,1975,212:315-313. [2] COIFMAN R, MEYER Y Y. Au Deldes commutators d’intégrals singuliéres et opérateurs multilinéaires[J]. Ann Inst Fourier(Grenoble),1978,28(3):177-202. [3] KEIGN E, STEIN M. Multilinear estimates and fractional integration[J]. Math Res Lett,1999,6(1):1-15. [4] GRAFAKOS L,TORRES R. Multilinear Calderon-Zygmund theory[J]. Adv Math,2002,165(1):124-164. [5] LACY M, THIECE C. Estimates on the bilinear Hilbert transform for 1 [6] 張普能,李亮. 多線性分數次積分算子在Herz型Hardy空間中的有界性[J]. 四川師范大學學報(自然科學版),2013,36(5):721-725. [7] 洪勇.Lp(Rn,ω(x))上的Hardy型奇異積分算子的范數[J]. 四川師范大學學報(自然科學版),2011,34(1):47-50. [8] 林燕. 多線性算子的有界性[J]. 數學物理學報,2008,A28(4):595-602. [9] 劉嵐喆,陸善鎮. 次線性算子在Herz型Hardy空間中的有界性[J]. 數學學報,2002,45(5):933-840. [10] SI Z Y.λ-centerl BMO estimates for multilinear commutators of fractional integral[J]. Actu Math Sinica:Engl Ser,2010,26(11):2093-2108. [11] PéREZ C, TORRES R. Sharp maximal function estimates for multilinear singular ineergrals[J]. Contempt Math,2003,320:323-331. [12] LERNER A, OMBROSI S, PREZ C. New maximal functions and multiple weights for the multilinear Calder on-Zygmund theory[J]. Adv Math,2009,220(4):1222-1264. [13] CHIRST M, GRAFAKOS L. Best constants for two non-convolution inequalities[J]. Proc Am Math Soc,1995,123(6):1687-1693. [14] 傅尊偉,劉宗光,陸善鎮.N維分數次Hardy算子交換子的特征[J]. 中國科學,2007,A50(10):1418-1426. [15] LU S Z, YANG D C. The decomposition of the weighted Herz spaces onRnand its applications[J]. Sci China,1995,A38(2):147-158. [16] LU S Z, YANG D C. The central BMO spaces and Littlewood-Paley operators[J]. Approx Theory Appl,1995,11(3):72-94. Estimate of the Commutators of Bilinear Fractional Hardy Operators on Herz-Morrey Spaces LIU Ronghui, ZHOU Jiang (CollegeofMathematicsandSystemSciences,XinjiangUniversity,Urumqi830046,Xinjiang) In this paper, it is proved that the commutators of bilinear operators and conjugate operators generated by central BMO functions and bilinear fractional Hardy operators are bounded on the Herz-Morrey, respectively. The similar results for bilinear Hardy operators and bilinear conjugate Hardy operators are also obtained. 2016-11-15 國家自然科學基金(11661075) *通信作者簡介:周 疆(1968—),男,教授,主要從事調和分析的研究,E-mail:zhoujiang@xju.edu.cn O174.2 A 1001-8395(2017)05-0621-07 10.3969/j.issn.1001-8395.2017.05.010 2010MSC:42B20; 42B45 (編輯 李德華)
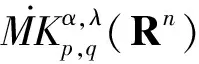
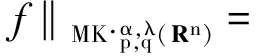
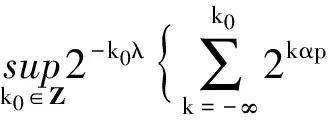
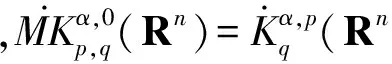
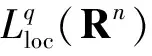
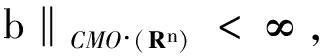
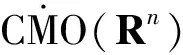
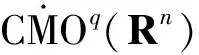
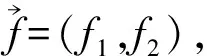
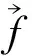
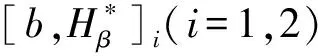
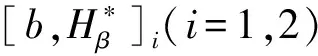
2 主要結論
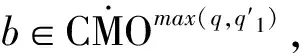
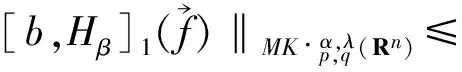
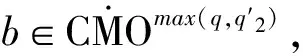
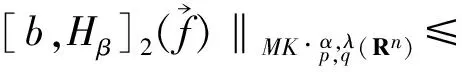
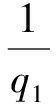
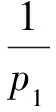
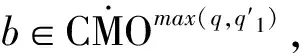
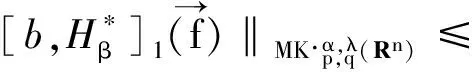
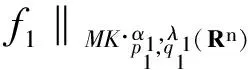
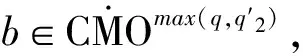
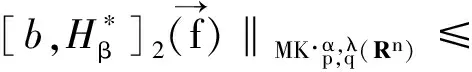
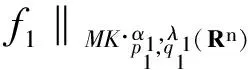
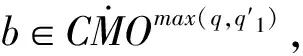
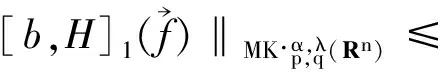
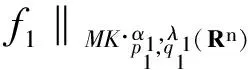
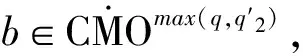
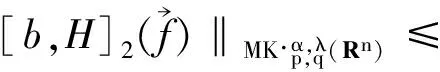
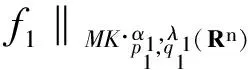
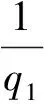
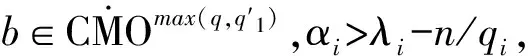
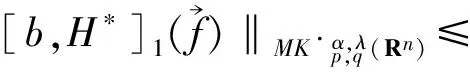
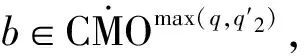
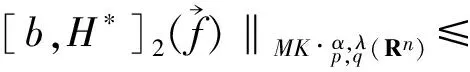
3 定理的證明