帶非局部擾動項的KdV方程的臨界正則性
王宏偉, 劉玉軍
(安陽師范學院 數學與統計學院, 河南 安陽 455000)
帶非局部擾動項的KdV方程的臨界正則性
王宏偉, 劉玉軍
(安陽師范學院 數學與統計學院, 河南 安陽 455000)

雙線性估計; Bourgain空間; 臨界正則性
本文研究如下帶非局部擾動項的KdV方程的Cauchy問題
(1)
其中,u=u(x,t)是未知函數,H表示Hilbert變換
y.
這類帶非局部擾動項的KdV方程是L. A. Ostrovsky等[1]在研究分層剪切流中非線性長波的輻射不穩定性問題時提出的數學模型.
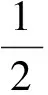



1 解空間和線性估計
A、B是2個正數,用AB表示存在c>0,使得A≤cB;如果c是一個充分小的正數,則用A?B來表示;當ABA時,記為A∽B.對u=u(x,t)∈S′(R2),Fxu或表示對空間變量x的Fourier變換或Fu表示時空Fourier變換.光滑函數η∈滿足η≥0,suppη?[-2,2],在[-1,1]上η≡1.定義φ(ξ)=η(ξ)-η(2ξ).N、L是二進制變量,即它們的取值是2n,n∈Z.定義算子PN為定義ψL(τ,ξ)=φL(τ-ξ3),即

考慮與方程(1)等價的積分方程

(2)

u(t)=η(t)[W(t)φ-
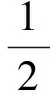

(3)

與方程(1)相聯系的一般的Bourgain空間Xs,b范數的定義是
‖u‖Xs,b=


‖u‖Xs,b,q=

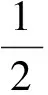

‖u‖X+Y=inf{‖u1‖X+‖u2‖Y:
u1∈X,u2∈Y,u=u1+u2}.
由空間Ss的定義,易知[7]如下引理.


(4)

(5)
利用Bourgain空間的理論,可以證明下面2個線性估計[7].


引理3定義線性算子
Lf(x,t)=



2 非線性估計


(6)
證明由空間S和N的定義,得到:


對u和v進行二進制分解有


(7)
為估計上式的右端,根據N、N1、N2的相對大小關系,需要分3種情況來計算:(a)N∽N2,N1N;(b)N∽N1,N2N;(c)N∽N1∽N2.根據對稱性,(a)和(b)的計算是相同的,因此,只須估計(a)和(c).
1) 如果N∽N2,N1N,此時(7)式右端可以改寫為

定理2轉化為證明如下不等式


(8)
對左邊進行二進制分解有
PN?x(PuPNv)=PNQL?x(PN1QL1uPNQL2v).
首先考慮最簡單的情況N11.利用空間的部分和Bernstein不等式,有





當NN11時,根據L、L1、L2的相對大小,分3種情況來討論.
(i)Lmax=L.此時,有LN2N1,由的定義和估計(4)、(5)式,可以得到





(ii)Lmax=L1.此時,有2種情況L1∽N2N1或L1∽LmedN2N1.如果L1∽N2N1,則





如果L1∽LmedN2N1,則Lmed=L2或Lmed=L,L1∽L∽Lmax∽Lmed的情況在Lmax=L時已經討論過了,因此不妨假定Lmed=L2,此時有








(iii)Lmax=L2.此時,L2∽N2N1,與前面的討論類似,可以得到








2)N?N1∽N2.此時,應用如下二進制分解
PN?N1?x(PN1uPN1v)=
由L1、L2的對稱性,不妨假定L1≥L2.低頻N1的情況容易計算





當N1時,分2種情況來證明結論.
(i)Lmax=L.此時,LN.如果對某個充分小的ε>0,有L1N1N2-ε,那么





當L2N1N2-ε時,與上面的估計相似.以下假定L1、L2N1N2-ε,此時有











最后,當L1∽L2時,得到





3 主要定理的證明

‖u‖Z=

對任何θ>0,存在μ=μ(θ)>0,使得對任何支集在[-T,T]內的光滑函數f有[7]

(9)

(10)
定義解映射

下面證明Γ(u)是壓縮的.
首先證明存在0 ‖L?x(uv)‖Z‖u‖Z‖v‖Z. (11) 把(11)式的左端分成3部分 ‖L?x(uv)‖Z‖ 由引理3和定理2可知 由(10)式可以得到 Tμ‖u2‖S 0‖v2‖S 0Tμα-2‖u‖Z‖v‖Z, Tμα-1‖u‖Z‖v‖Z. 合并以上3個估計有 ‖L?x(uv)‖Z (1+(α-2+α-1)Tμ)‖u‖Z‖v‖Z, 即當T∽α2≤1時(11)式成立. 下面把初值分解為低頻和高頻2部分,即φ=Pφ+P?Nφ.取定β>0,令N充分大,可以得到 由引理1,‖η(·)W(·)P?Nφ‖Zβ.另外,根據Z的定義有 ‖η(·)W(·)P?Nφ‖S 0 α‖Pφ‖L2‖ 適當選取充分小的β,使得α‖則Γ(u)是Z上的一個壓縮映射.定理1得到證明. 致謝安陽師范學院科研培育基金(AYNU-KP-B04)對本文給予了資助,謹致謝意. [1] OSTROVSKY L A, STEPANYAMS Y A, TSIMRING L S. Radiation instability in a stratified shear flow[J]. Int J NonLinear Mech,1984,19(4):151-161. [2] ALVAREZ B. The Cauchy problem for a nonlocal perturbation of the KdV equation[J]. Diff Integ Eqns,2003,16(10):1249-1280. [3] CARVAJALD X, SCIALOM M. On the well-posedness for the generalized Ostrovsky, Stepanyams and Tsimring equation[J]. Nonlinear Anal,2005,62(7):1277-1287. [4] ZHAO X, CUI S. Well-posedness of the Cauchy problem for Ostrovsky, Stepanyams and Tsimring equation with low regularity data[J]. J Math Anal Appl,2008,344(2):778-787. [5] MOLINET L, RIBAUD F. The Cauchy problem for dissipative Korteweg-de Vries equations in Sobolev spaces of negative order[J]. Indiana Univ Math J,2001,50(4):1745-1776. [6] MOLINET L, RIBAUD F. The global Cauchy problem in Bourgain's type spaces for a dispersive dissipative semilinear equation[J]. SIAM J Math Anal,2002,33(6):1269-1296. [7] MOLINET L, RIBAUD F. On the low regularity of the Korteweg-de Vries-Burgers equation[J]. Int Math Res Not,2002,37(6):1979-2005. [8] KENIG C E, PONCE G, VEGA L. A bilinear estimate with applications to the KdV equation[J]. J Am Math Soc,1996,9(2):573-603. [9] ZHAO X, CUI S. Local well-posedness of the Ostrovsky, Stepanyams and Tsimring equation in Sobolev spaces of negative indices[J]. Nonlinear Anal,2009,70(10):3483-3501. [10] CARVAJAL X, PANTHEE M. Panthee, well-posedness of KdV type equations[J]. Electron J Diff Eqns,2012,2012(40):1-15. [11] CARVAJAL X, PANTHEE M. Well-posedness for for some perturbations of the KdV equation with low regularity data[J]. Electron J Diff Eqns,2008,2008(2):1-18. [12] PILOD D. Sharp well-posedness results for the Kuramoto-Velarde equation[J]. Commun Pure Appl Anal,2008,7(4):867-881. [13] 林雪梅,胡勁松,劉倩. 耗散SRLW方程的一個新的守恒差分逼近[J]. 四川師范大學學報(自然科學版),2014,37(1):49-53. [14] 廖歐,舒級,曾群香. 一類混合KdV方程的精確孤立波解[J]. 四川師范大學學報(自然科學版),2015,38(4):493-496. [15] ESFAHANI A. Sharp well-posedness of the Ostrovsky, Stepanyams and Tsimring equation[J]. Math Commun,2013,18(2):323-335. On the Critical Regularity of the KdV Equation with a Nonlocal Perturbation WANG Hongwei, LIU Yujun (SchoolofMathematicalandStatistics,AnyangNormalUniversity,Anyang455000,Henan) bilinear estimate; Bourgain space; critical regularity 2016-03-03 國家自然科學基金(11401460)和河南省教育廳高等學校重點科研項目(14B110028、16A110007) 王宏偉(1977—), 男,副教授,主要從事偏微分方程和調和分析的研究,E-mail:wanghw@aynu.edu.cn O175.29 A 1001-8395(2017)05-0639-05 10.3969/j.issn.1001-8395.2017.05.013 2010MSC:35Q53; 35Q07 (編輯 陶志寧)











