雙層金屬納米板界面能密度的尺寸效應(yīng)1)
王 帥 姚 寅 楊亞政 ?,? 陳少華
?(中國(guó)科學(xué)院力學(xué)研究所非線性力學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室,北京100190)
?(北京理工大學(xué)先進(jìn)結(jié)構(gòu)技術(shù)研究院,輕量化多功能復(fù)合材料與結(jié)構(gòu)北京市重點(diǎn)實(shí)驗(yàn)室,北京100081)
??(北京理工大學(xué)北京電動(dòng)車輛協(xié)同創(chuàng)新中心,北京100081)
??(中國(guó)科學(xué)院大學(xué)工程科學(xué)學(xué)院,北京100049)
雙層金屬納米板界面能密度的尺寸效應(yīng)1)
王 帥?,??姚 寅?楊亞政?,??陳少華?,??,2)
?(中國(guó)科學(xué)院力學(xué)研究所非線性力學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室,北京100190)
?(北京理工大學(xué)先進(jìn)結(jié)構(gòu)技術(shù)研究院,輕量化多功能復(fù)合材料與結(jié)構(gòu)北京市重點(diǎn)實(shí)驗(yàn)室,北京100081)
??(北京理工大學(xué)北京電動(dòng)車輛協(xié)同創(chuàng)新中心,北京100081)
??(中國(guó)科學(xué)院大學(xué)工程科學(xué)學(xué)院,北京100049)
界面能密度是表征納米復(fù)合材料與結(jié)構(gòu)界面力學(xué)性質(zhì)的重要物理量.采用分子動(dòng)力學(xué)方法計(jì)算了不同面心立方金屬晶體構(gòu)成的雙材料納米薄板結(jié)構(gòu)的界面能密度,分析了界面晶格結(jié)構(gòu)形貌變化及界面效應(yīng)對(duì)原子勢(shì)能的影響.結(jié)果表明:雙材料納米薄板界面具有周期性褶皺狀疏密相間的晶格結(jié)構(gòu)形貌,界面上原子勢(shì)能亦呈現(xiàn)周期性分布特性,而靠近界面的兩側(cè)原子勢(shì)能與板內(nèi)原子勢(shì)能具有明顯差異.拉格朗日界面能密度和歐拉界面能密度均隨雙層薄板厚度的增加而增加,最終趨向于塊體雙材料結(jié)構(gòu)的界面能密度.
雙材料金屬界面,分子動(dòng)力學(xué),界面能密度,尺寸效應(yīng),界面形貌
引言
由于納米結(jié)構(gòu)材料具有較大的比表/界面積(表/界面積與體積之比),納尺度的表/界面性質(zhì)對(duì)納米材料與結(jié)構(gòu)整體力學(xué)性能產(chǎn)生不可忽略的影響[13],即表/界面效應(yīng).納米復(fù)合材料及雙材料納米層合板結(jié)構(gòu)作為典型的多相納米結(jié)構(gòu)材料,其內(nèi)部界面效應(yīng)導(dǎo)致材料及結(jié)構(gòu)物性表現(xiàn)出宏觀復(fù)合材料與結(jié)構(gòu)不涉及的尺寸相關(guān)性,這一特性使得在微電子制造、高效節(jié)能電池及生物醫(yī)學(xué)等新興工業(yè)領(lǐng)域中廣泛應(yīng)用的納米復(fù)合材料與結(jié)構(gòu)的性能更受關(guān)注[4].如何合理表征界面效應(yīng),對(duì)于納米復(fù)合材料與結(jié)構(gòu)的設(shè)計(jì)和應(yīng)用具有重要的意義.
現(xiàn)有納米材料與結(jié)構(gòu)界面效應(yīng)的表征理論主要基于Gurtin和Murdoch提出的表面彈性理論[56]而建立:即將納米復(fù)合材料與結(jié)構(gòu)的界面視為無厚度層,但符合線彈性本構(gòu)關(guān)系,并具有獨(dú)立的界面彈性常數(shù),建立了界面應(yīng)力與界面應(yīng)變的線彈性關(guān)系.Sharma等[7],Mogilevskaya等[8]將該理論與復(fù)合材料細(xì)觀力學(xué)相結(jié)合,給出與納米夾雜尺寸和界面彈性常數(shù)相關(guān)的艾雪比(Eshelby)張量,并揭示了界面效應(yīng)對(duì)納米復(fù)合材料等效剛度的影響.假設(shè)界面具有共格結(jié)構(gòu)(界面變形與鄰近體材料變形相同),可以建立考慮界面彈性的非均質(zhì)材料細(xì)觀力學(xué)框架[912].黃筑平等[1315]進(jìn)一步給出了有限變形框架下的界面應(yīng)力和界面能密度的拉格朗日和歐拉表述.
基于Gurtin-Murdoch模型(G-M)的界面效應(yīng)表征理論的主要特點(diǎn)是引入界面彈性常數(shù)作為表征界面特性的關(guān)鍵參數(shù).然而,在很多實(shí)際應(yīng)用中,界面彈性常數(shù)的取值無據(jù)可依,極大程度地限制了已有界面效應(yīng)彈性理論的實(shí)際應(yīng)用[16].即使在已有的多個(gè)表面效應(yīng)彈性理論中,表面彈性常數(shù)的獲得也比較困難,目前只能通過復(fù)雜的分子動(dòng)力學(xué)計(jì)算給出[1718],且理論模型的無厚度假設(shè)與分子動(dòng)力學(xué)模型的原子連續(xù)性假設(shè)亦存在不一致性,導(dǎo)致計(jì)算結(jié)果分散,甚至不確定性.為了避免表面彈性常數(shù)的引入,采用原子晶格模型,Chen等[19]提出了一種基于表面自由能密度的彈性理論,主要涉及塊體材料的表面能密度和納米材料的表面晶格弛豫系數(shù);考慮納米復(fù)合材料的共格界面,界面能密度僅與納米相和基體表面的晶格弛豫參數(shù)及失配變形相關(guān),進(jìn)一步基于界面能密度建立了一種描述共格界面的新彈性理論[20],避免了已有界面效應(yīng)彈性理論中界面彈性常數(shù)的引入.
上述理論中,界面能密度是表征納米復(fù)合材料界面效應(yīng)的關(guān)鍵物理量[2122].隨著納米復(fù)合材料特征尺寸的減小,比界面積增大,界面區(qū)域的能量狀態(tài)將發(fā)生顯著變化,界面能密度表現(xiàn)出尺寸相關(guān)性.
為了更直觀地從原子尺度理解界面能密度的尺寸相關(guān)性,本文采用分子動(dòng)力學(xué)方法對(duì)界面能密度的尺寸效應(yīng)進(jìn)行了數(shù)值研究和分析.采用相對(duì)簡(jiǎn)單的面心立方金屬晶體構(gòu)成的雙材料納米薄板系統(tǒng)作為研究對(duì)象,建立分子動(dòng)力學(xué)模型,計(jì)算不同金屬雙材料界面的拉格朗日界面能密度和歐拉界面能密度,分析界面處晶格構(gòu)型形貌及界面原子自由能的分布特征,最終揭示界面能密度和雙材料薄板厚度的尺寸相關(guān)性.本文的研究結(jié)果對(duì)含不同形式界面的納米材料界面效應(yīng)彈性理論建立,以及對(duì)納米復(fù)合材料與結(jié)構(gòu)的設(shè)計(jì)和應(yīng)用都具有一定的理論指導(dǎo)意義.
1 分子動(dòng)力學(xué)模型
1.1 雙材料納米薄板
考慮若干面心立方金屬晶體構(gòu)成的雙材料納米薄板系統(tǒng)(Ag/Cu,Ag/Ni,Au/Cu,Au/Ni和Pd/Cu),建立如圖1所示的分子動(dòng)力學(xué)模型(紅色和藍(lán)色分別代表不同的金屬材料).
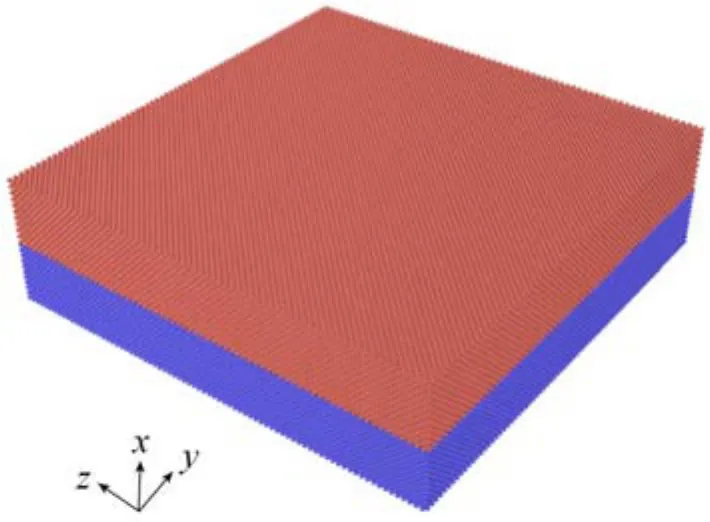
圖1 面心立方金屬雙材料薄板結(jié)構(gòu)分子動(dòng)力學(xué)模型Fig.1 Molecular dynamics model of FCC metallic bi-material nano-plates
圖1中,y軸和z軸方向?yàn)橹芷谛赃吔鐥l件,x軸方向?yàn)榉侵芷谛赃吔鐥l件(為納米厚度方向,存在結(jié)構(gòu)的上下表面).由于界面兩側(cè)金屬材料的晶格常數(shù)并不相同,需要引入界面失配應(yīng)變以滿足界面區(qū)域的幾何協(xié)調(diào)條件[17]
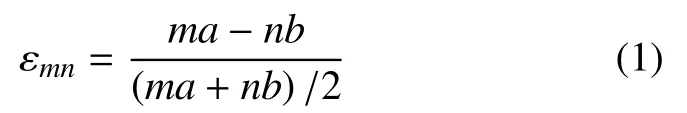
式中,a和b分別表示形成界面的兩種金屬材料的晶格常數(shù),m和n表示兩種金屬在薄板面內(nèi)方向的晶胞數(shù)目,即形成界面的兩種金屬材料邊長(zhǎng)分別是ma和nb.當(dāng)界面處殘余失配應(yīng)變足夠小時(shí)(εmn≤0.05%),該殘余應(yīng)變幾乎不會(huì)影響界面能密度的變化趨勢(shì),且有ma≈nb.由于兩種晶體的晶格長(zhǎng)度有一定的差別,界面原子不可能完全一一對(duì)應(yīng),在界面上產(chǎn)生一定的位錯(cuò),形成半共格界面.
采用EAM勢(shì)函數(shù)描述原子間的相互作用[23]
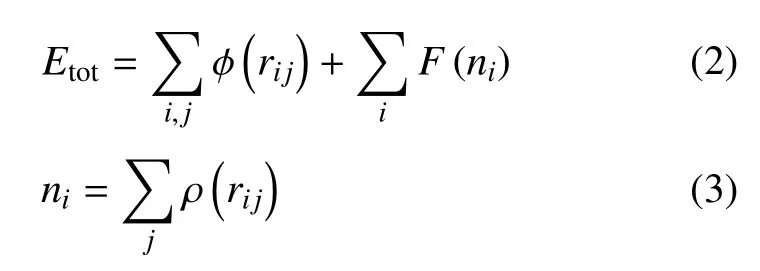
其中,i,j分別表示第i和第 j個(gè)原子,rij表示i原子和 j原子之間的距離,F(xiàn)(ni)表示i原子上的嵌入能,表示i原子和 j原子之間的二體勢(shì).
本文采用LAMMPS[24]軟件進(jìn)行分子動(dòng)力學(xué)計(jì)算.從塊體雙材料系統(tǒng)的界面附近截取納米厚度雙材料薄板,使用Nose-Hoover控溫方法令納米薄板在恒溫恒壓下充分弛豫,本文壓強(qiáng)為0,溫度為1K.弛豫計(jì)算的時(shí)間步長(zhǎng)設(shè)置為1fs,在經(jīng)歷足夠時(shí)間的充分弛豫(500ps)后,系統(tǒng)達(dá)到穩(wěn)定狀態(tài).記錄并輸出當(dāng)前狀態(tài)下各原子的勢(shì)能及原子坐標(biāo)信息.
1.2 界面能密度的計(jì)算
選取界面附近沿x軸方向一定厚度區(qū)域內(nèi)的原子計(jì)算界面能,雙材料納米薄板系統(tǒng)的界面自由能可以寫成
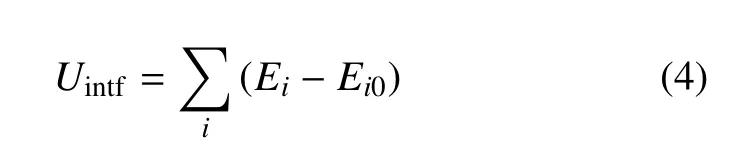
其中,Ei是界面區(qū)域內(nèi)第i個(gè)原子弛豫后的原子勢(shì)能.Ei0是第 i個(gè)原子在相應(yīng)塊體材料中的原子勢(shì)能,在數(shù)值上等于負(fù)的原子內(nèi)聚能[17,25].
假設(shè)雙材料界面弛豫前和弛豫后的面積分別是AL和 AE,則有 AL=L10L20,AE=L1L2.其中,L10和L20分別表示弛豫前構(gòu)型(初始構(gòu)型)中界面在y軸和z軸方向的初始長(zhǎng)度.L1和L2分別表示弛豫后構(gòu)型中(當(dāng)前構(gòu)型)界面在y軸和z軸方向的當(dāng)前長(zhǎng)度.拉格朗日界面能密度和歐拉界面能密度可以寫為[17,20,26]式中,γL和γE分別表示雙材料納米薄板界面能密度的拉格朗日描述和歐拉描述.
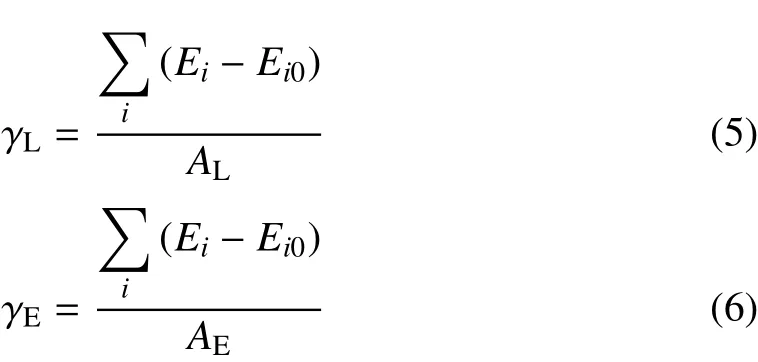
2 計(jì)算結(jié)果與討論
2.1 界面原子結(jié)構(gòu)形貌
由于界面處原子與內(nèi)部原子的鍵合狀態(tài)不同,界面原子具有大量的不飽和原子鍵,界面區(qū)域原子的能量和原子平衡狀態(tài)與內(nèi)部區(qū)域原子相比將發(fā)生明顯變化.當(dāng)兩種材料形成半共格界面時(shí),除了界面處原子的配位不飽和性,兩種材料晶格常數(shù)的不同還將導(dǎo)致界面處形成較為復(fù)雜的原子結(jié)構(gòu)形貌.下文以Ag/Cu納米薄板的分子動(dòng)力學(xué)計(jì)算為例對(duì)界面原子形貌進(jìn)行詳細(xì)分析.
圖2給出納米薄板發(fā)生弛豫后界面原子相對(duì)其平均位置的位移,?x,?y和?z分別表示在x,y和z方向的位移分量.可以看出?x,?y和?z在界面內(nèi)呈周期性分布,這主要是形成半共格界面的兩種材料晶格不匹配引起的:例如Ag表面某一個(gè)原子周圍的Ag原子排布是相同的,但是該原子周圍Cu原子的分布卻由于晶格不匹配而呈現(xiàn)周期性變化.Ag和Cu原子沿x軸的位移始終保持同方向,即同時(shí)凸起或同時(shí)凹陷;而沿y或z軸的位移則方向相反.界面原子相對(duì)其平均位置的位移最終導(dǎo)致界面形成褶皺狀疏密相間的周期性晶格結(jié)構(gòu)形貌.為了更直觀地展示界面原子的微結(jié)構(gòu)形貌,將?x,?y和?z分別擴(kuò)大為原來的5倍,得到如圖3所示的界面微觀形貌圖,可以看出雙材料金屬納米板弛豫之后,界面呈現(xiàn)出褶皺狀疏密相間的晶體結(jié)構(gòu).
2.2 原子勢(shì)能
界面處原子排布和內(nèi)部原子不同,必然導(dǎo)致界面區(qū)域的能量和原子平衡狀態(tài)與內(nèi)部相比呈現(xiàn)出明顯的不同.如圖4所示,對(duì)應(yīng)界面的周期性褶皺結(jié)構(gòu),界面原子的勢(shì)能(原子自由能)變化也呈現(xiàn)周期性分布.為進(jìn)一步了解界面原子勢(shì)能與體內(nèi)原子勢(shì)能的差異,圖5給出原子勢(shì)能沿納米薄板厚度方向的分布,圖示表明表面原子勢(shì)能明顯高于體內(nèi)原子勢(shì)能,而界面區(qū)域,即在x=0位置附近,原子勢(shì)能與體內(nèi)原子勢(shì)能亦不相同.在遠(yuǎn)離表/界面處,納米板內(nèi)部原子的原子勢(shì)能迅速趨于塊體材料中的原子勢(shì)能,這與已有的理論研究一致[2627].
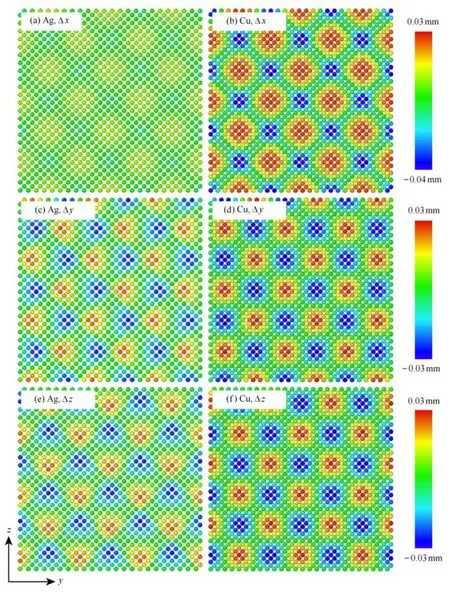
圖2 Ag/Cu雙材料納米薄板界面原子相對(duì)平均位置的位移分布云紋圖Fig.2 Contour plots of displacement of atoms from their average positions at the Ag/Cu nano-plate interface
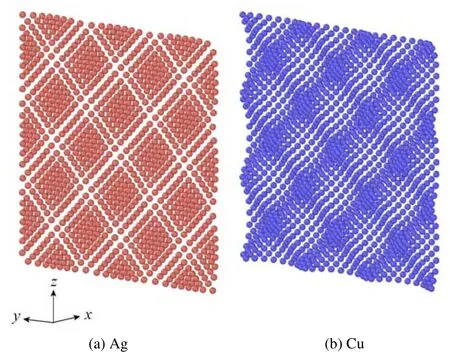
圖3 Ag/Cu雙材料納米薄板界面原子形貌圖Fig.3 The morphology of lattice structures at the Ag/Cu nano-plate interface
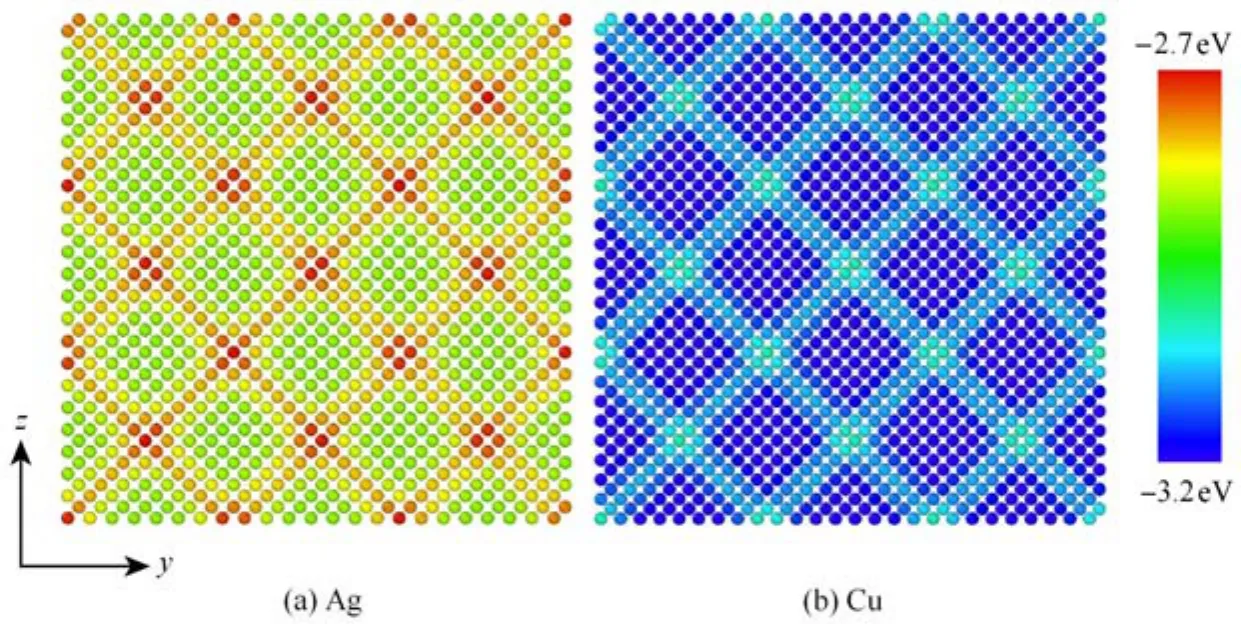
圖4 Ag/Cu雙材料納米薄板界面處原子勢(shì)能分布云紋圖Fig.4 Potential energy of atoms at the Ag/Cu interface
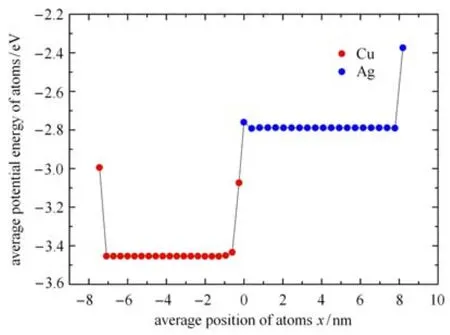
圖5 Ag/Cu雙材料納米薄板原子勢(shì)能沿厚度方向的變化Fig.5 Variation of the free energy of atoms in the thickness direction
因此,可以采用界面附近區(qū)域內(nèi)原子勢(shì)能計(jì)算界面能密度.由前述勢(shì)能分布可知,當(dāng)離開界面超過三層原子以后,其原子勢(shì)能就幾乎不再發(fā)生變化.進(jìn)一步研究表明,針對(duì)足夠厚的雙材料,在界面附近2nm厚的區(qū)域與更厚區(qū)域計(jì)算的界面能密度差別很小.在實(shí)際計(jì)算中,采用厚度為8nm的區(qū)域來計(jì)算雙材料納米結(jié)構(gòu)的界面能密度.而對(duì)于厚度較小的雙材料,界面區(qū)厚度取為整個(gè)雙材料厚度的一半(例如,厚度為5nm的雙材料納米板,則采用2.5nm厚度內(nèi)的原子來計(jì)算界面能密度),這樣可以盡可能減小表面原子對(duì)界面能密度計(jì)算的影響.而對(duì)于厚度更小的雙材料結(jié)構(gòu),由于其表面原子和界面原子距離較小,表面的存在必將對(duì)界面能密度產(chǎn)生非常明顯的影響,本文未考慮該種情況.
2.3 雙層納米薄板的界面能密度
本文計(jì)算了多種面心立方金屬晶體材料構(gòu)成的半共格界面的拉格朗日界面能密度和歐拉界面能密度.圖6給出界面能密度隨納米薄板厚度的變化趨勢(shì),可以看出拉格朗日界面能密度和歐拉界面能密度均隨薄板厚度的增大而增大,并逐漸趨于塊體雙材料系統(tǒng)中的界面能密度γ0.這說明納米復(fù)合材料中的界面效應(yīng)影響將隨材料或結(jié)構(gòu)特征尺寸的增大而逐漸減弱.
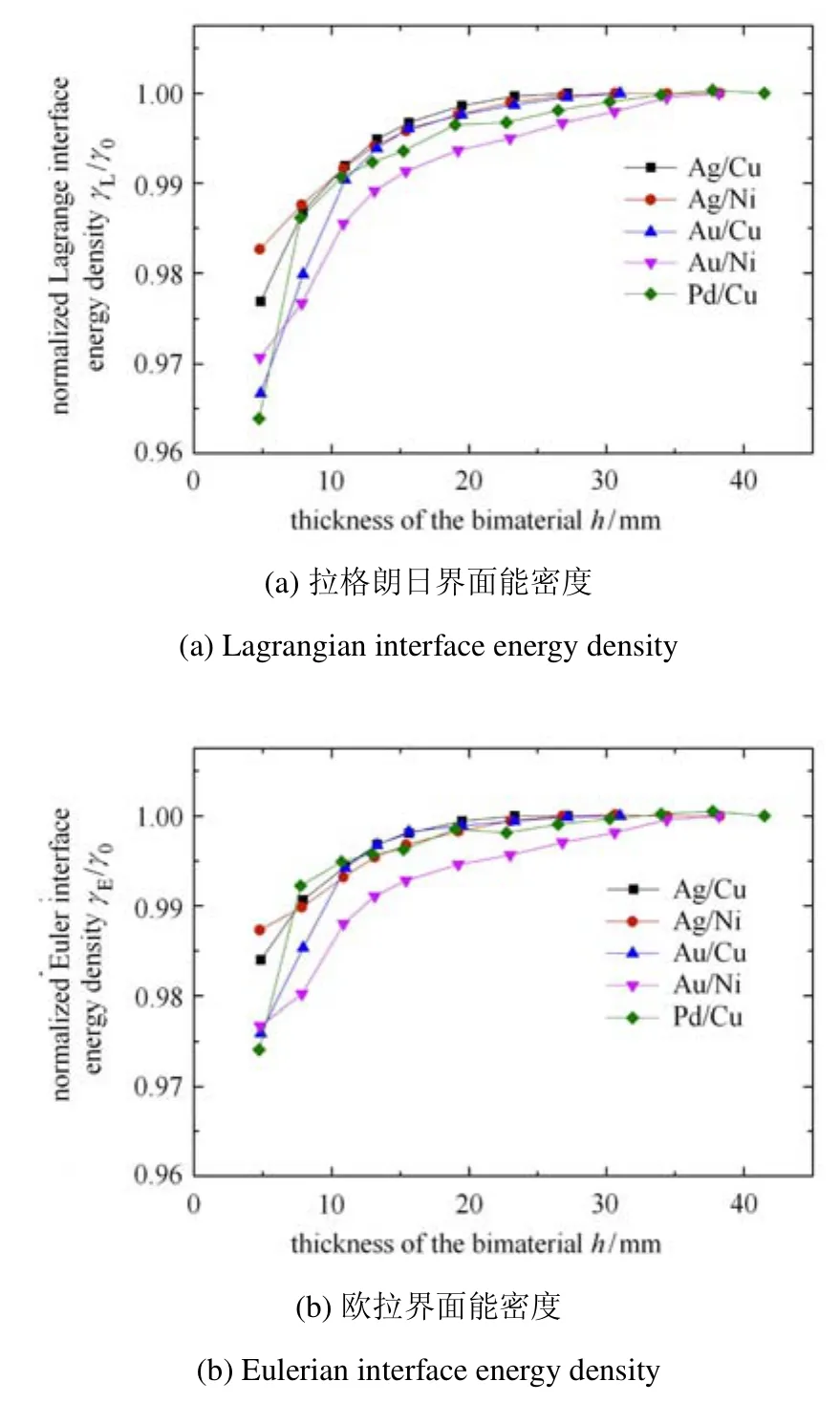
圖6 雙材料金屬納米薄板結(jié)構(gòu)的界面能密度Fig.6 Interface energy density of metallic bi-material nano-plates
理論上,納米材料界面能密度具有如下形式[28]

本文計(jì)算模型中,由于雙材料納米薄板存在上下表面,當(dāng)雙材料薄板厚度較小時(shí)(小于5nm),表面和界面較為接近,表面附近原子的配位不飽和狀態(tài)將對(duì)界面能密度產(chǎn)生一定影響;但當(dāng)板厚較大時(shí),更接近塊體雙材料板結(jié)構(gòu),表面和界面相距較遠(yuǎn),彼此之間的影響可以忽略.如圖6所示,板厚小于5nm時(shí),拉格朗日界面能密度和歐拉界面能密度的變化曲線表現(xiàn)出一定波動(dòng);而當(dāng)板厚超過10nm時(shí),拉格朗日界面能密度和歐拉界面能密度的變化曲線相對(duì)光滑.說明結(jié)構(gòu)特征尺寸較小時(shí),表面會(huì)對(duì)界面能密度產(chǎn)生一定的影響.
由上可見,雙材料納米板界面能密度隨厚度的變化趨勢(shì)與單一金屬納米薄板表面能密度的尺寸效應(yīng)有一定的差別.已有結(jié)果顯示:在金屬納米板(100)面上,拉格朗日表面能密度隨納米板厚度的增大而增大,而歐拉表面能密度則隨納米板厚的增大而減小[25].本文得到的拉格朗日界面能密度及歐拉界面能密度都隨雙層板厚的增大而逐漸增大.該現(xiàn)象可以通過分析拉格朗日界面能密度和歐拉界面能密度的關(guān)系來加以理解[17,20,26].弛豫后界面表觀面積可以寫為
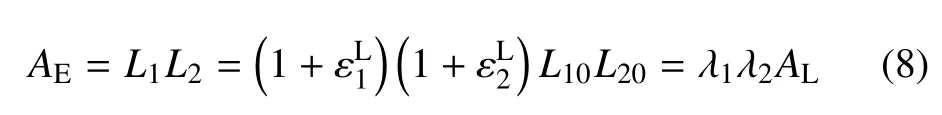

可見,歐拉界面能密度與拉格朗日界面能密度和界面弛豫參數(shù)相關(guān).圖6(a)與圖7對(duì)比發(fā)現(xiàn),隨著板厚的增大,界面弛豫參數(shù)的變化相對(duì)較小,而拉格朗日界面能密度的增大更為明顯,從而使歐拉界面能密度呈現(xiàn)隨厚度增大而增大的整體變化趨勢(shì).而在金屬納米板表面能密度的研究中,拉格朗日表面能密度和表面弛豫參數(shù)雖然也同時(shí)隨納米板厚的增大而增大,但拉格朗日表面能密度的變化相比表面弛豫參數(shù)的變化較小,從而使得歐拉表面能密度呈現(xiàn)隨厚度增大而減小的趨勢(shì)[25].這也說明雙材料間的相互約束,使得界面弛豫變形相比單一納米板表面的弛豫變形要小.

圖7 雙材料界面弛豫參數(shù)隨厚度的變化Fig.7 The interface relaxation parameter of bi-nano-plates as a function of the structure’s thickness
3 結(jié)論
本文采用分子動(dòng)力學(xué)方法,研究了多種面心立方金屬晶體構(gòu)成的雙材料納米薄板的界面微結(jié)構(gòu)、原子勢(shì)能、界面弛豫變形等界面性質(zhì),計(jì)算了拉格朗日界面能密度和歐拉界面能密度.結(jié)果表明:不同面心立方金屬晶體形成的半共格界面,其界面處原子具有周期性排布,界面呈現(xiàn)周期性褶皺狀疏密相間的形貌.界面處原子配位和分布與內(nèi)部原子的差異導(dǎo)致平衡狀態(tài)下界面原子的能量與內(nèi)部原子存在較大差異,引起納米尺度的界面效應(yīng).雙材料納米薄板的拉格朗日界面能密度和歐拉界面能密度都隨雙層板厚的增大而增大,并最終趨于宏觀雙材料結(jié)構(gòu)中的界面能密度.
1 GleiterH.Nanostructuredmaterials:Basicconceptsandmicrostructure.Acta Materialia,2000,48(1):1-29
2 M¨uller P,Sa′ul A.Elastic e ff ects on surface physics.Surface Science Reports,2004,54(5-8):157-258
3 Ibach H.The role of surface stress in reconstruction,epitaxial growth and stabilization of mesoscopic structures.Surface Science Reports,1997,29(5-6):195-263
4張玉龍.納米復(fù)合材料手冊(cè).北京:中國(guó)石化出版社,2005(Zhang Yulong.Handbook of Nano-composites.Beijing:China Petrochemical Press,2005(in Chinese))
5 Gurtin ME,Murdoch AI.Surface stress in solids.International Journal of Solids and Structures,1978,14(6):431-440
6 Gurtin ME,Murdoch AI.A continuum theory of elastic material surfaces.Archive for Rational Mechanics and Analysis,1975,57(4):291-323
7 Sharma P,Ganti S.Size-dependent Eshelby’s tensor for embedded nano-inclusions incorporating surface/interface energies.Journal of Applied Mechanics,2004,71(5):663-671
8 Mogilevskaya SG,Crouch SL,La Grotta A,et al.The e ff ects of surface elasticity and surface tension on the transverse overall elastic behavior of unidirectional nano-composites.Composites Science and Technology,2010,70(3):427-434
9 Duan H,Wang J,Huang Z,et al.Size-dependent e ff ective elastic constants of solids containing nano-inhomogeneities with interface stress.Journal of the Mechanics and Physics of Solids,2005,53(7):1574-1596
10 Li Z,Lim C,He L.Stress concentration around a nano-scale spherical cavity in elastic media:E ff ect of surface stress.European Journal of Mechanics-A/Solids,2006,25(2):260-270
11 Li P,Wang Q,Shi S.Di ff erential scheme for the e ff ective elastic properties of nano-particle composites with interface e ff ect.Computational Materials Science,2011,50(11):3230-3237
12 Dai M,Gao C-F.Non-circular nano-inclusions with interface e ff ects that achieve uniform internal strain fi elds in an elastic plane under anti-plane shear.Archive of Applied Mechanics,2016,86(7):1295-1309
13 Huang Z,Wang J.A theory of hyperelasticity of multi-phase media with surface/interface energy e ff ect.Acta Mechanica,2006,182(3-4):195-210
14 Wang Z-Q,Zhao Y-P,Huang Z-P.The e ff ects of surface tension on the elastic properties of nano structures.International Journal of Engineering Science,2010,48(2):140-150
15 Gao X,Huang Z,Qu J,et al.A curvature-dependent interfacial energy-based interface stress theory and its applications to nanostructured materials:(I)General theory.Journal of the Mechanics and Physics of Solids,2014,66:59-77
16 Miller RE,Shenoy VB.Size-dependent elastic properties of nanosized structural elements.Nanotechnology,2000,11(3):139
17 Mi C,Jun S,Kouris DA,et al.Atomistic calculations of interface elastic properties in noncoherent metallic bilayers.Physical Review B,2008,77(7):075425
18 Paliwal B,Cherkaoui M.Atomistic–continuum interphase model for e ff ective properties of composite materials containing nanoinhomogeneities.Philosophical Magazine,2011,91(30):3905-3930
19 Chen S,Yao Y.Elastic theory of nanomaterials based on surfaceenergy density. Journal of Applied Mechanics,2014,81(12):121002
20 Yao Y,Chen S,Fang D.An interface energy density-based theory considering the coherent interface e ff ect in nanomaterials.Journal of the Mechanics and Physics of Solids,2017,99:321-337
21 Shuttleworth R.The surface tension of solids.Proceedings of the Physical Society.Section A,1950,63(5):444
22 Cammarata R.Surface and interface stress e ff ects on interfacial and nanostructured materials.Materials Science and Engineering:A,1997,237(2):180-184
23 Johnson R.Alloy models with the embedded-atom method.Physical Review B,1989,39(17):12554
24 Plimpton S.Fast parallel algorithms for short-range molecular dynamics.Journal of Computational Physics,1995,117(1):1-19
25 Zhang C,Yao Y,Chen S.Size-dependent surface energy density of typically fcc metallic nanomaterials.Computational Materials Science,2014,82(3):372-377
26 Dingreville R,Qu J.Interfacial excess energy,excess stress and excess strain in elastic solids:planar interfaces.Journal of the Mechanics and Physics of Solids,2008,56(5):1944-1954
27 Spearot D,Capolungo L,Qu J,et al.On the elastic tensile deformation of〈100〉bicrystal interfaces in copper.Computational Materials Science,2008,42(1):57-67
28 Ouyang G,Liang L,Wang C,et al.Size-dependent interface energy.Applied Physics Letters,2006,88(9):091914
29 Jiang Q,Li J,Chi B.Size-dependent cohesive energy of nanocrystals.Chemical Physics Letters,2002,366(5):551-554
SIZE EFFECT OF THE INTERFACE ENERGY DENSITY IN BI-NANO-SCALED-METALLIC PLATES1)
Wang Shuai?,??Yao Yin?Yang Yazheng?,??Chen Shaohua?,??,2)?(LNM,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China)?(Institute of Advanced Structure Technology,Beijing Key Laboratory of Lightweight Multi-functional Composite Materials and Structures,Beijing
Institute of Technology,Beijing 100081,China)
??(Collaborative Innovation Center of Electric Vehicles in Beijing,Beijing Institute of Technology,Beijing 100081,China)??(School of Engineering Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)
The interface free energy density is an important quantity characterizing the mechanical property of interface in nanocomposite systems.In this paper,molecular dynamics simulation method is adopted to investigate the interface energy density of di ff erent FCC metallic bi-nano-scaled plates.The morphology of the interface crystal structure and the interface e ff ect on the atomic potential are analyzed.It is found that interface atoms have periodically wrinkled rare fi ed or serried con fi gurations,and the potential energy of interface atoms is also periodically distributed.The potential energy of atoms near the interface is obviously di ff erent from that of atoms inside the nano-plates.Both the Lagrange interface energy and the Eulerian one increase with the increase of the thickness of the bi-material,which approach the interface energy of a bulk bi-material fi nally.
metallicbi-materialinterface,moleculardynamics,interfaceenergydensity,sizee ff ect,interfacemorphology
O485
A
10.6052/0459-1879-17-142
2017–04–28收稿,2017–06–30 錄用,2017–06–30 網(wǎng)絡(luò)版發(fā)表.
1)國(guó)家自然科學(xué)基金(11372317,11532013,11402270)和北京理工大學(xué)科研創(chuàng)新計(jì)劃資助項(xiàng)目.
2)陳少華,教授,主要研究方向:微納米力學(xué),表面/界面力學(xué),仿生材料力學(xué)及功能化表面研制.E-mail:shchen@bit.edu.cn
王帥,姚寅,楊亞政,陳少華.雙層金屬納米板界面能密度的尺寸效應(yīng).力學(xué)學(xué)報(bào),2017,49(5):978-984
Wang Shuai,Yao Yin,Yang Yazheng,Chen Shaohua.Size e ff ect of the interface energy density in bi-nano-scaled-metallic plates.
Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):978-984

