深溝球軸承運轉過程顯式動力學數值仿真研究

陳曙光 張洪偉 蔡曉君

(北京石油化工學院機械工程學院)

深溝球軸承運轉過程顯式動力學數值仿真研究

陳曙光 張洪偉 蔡曉君

(北京石油化工學院機械工程學院)

基于顯式動力學有限元理論，應用ANSYS/LS-DYNA軟件建立了6014深溝球軸承的多體接觸力學模型。考慮轉速和徑向載荷的作用，在一定工況條件下進行了動力學仿真研究，分析了軸承運轉過程中動態響應與接觸應力的變化規律。結果表明：仿真結果與理論計算結果相吻合。

深溝球軸承 顯式動力學 接觸碰撞 有限元模型

滾動軸承是傳遞運動和承受載荷的重要支撐轉動部件[1,2]。隨著旋轉機械朝著高轉速、高穩定性、低噪聲和低振動的方向發展，滾動軸承的動態性能問題日益突出[3～5]。因此，對軸承進行動力學分析，掌握其接觸應力分布規律具有重要意義。

滾動軸承的力學模型經歷了4個發展過程：靜力學分析、擬靜力學分析、擬動力學分析和動力學分析[5]。近年來，有限元方法、接觸算法等的不斷發展，促進了滾動軸承三維數值仿真的發展[6～11]。Stone B J利用計算機仿真模擬分析了球軸承中鋼球運動與摩擦特性的關系，結果表明，軸承工作時由于滾動體滾動而產生的離心力對軸承疲勞壽命會產生很大影響，限制了軸承最高轉速[6]。Wang J等采用全數值分析法，分別在純滾動、滑移-滾動、純滑動3種條件下進行了研究[7]。文獻[8,11]利用ANSYS/LS-DYNA對滾動軸承的運動過程進行了仿真分析。唐云冰等利用ANSYS研究了滾動軸承的載荷分布[10]。SKF、NSK及FAG等公司逐步采用有限元仿真軟件對滾動軸承的應力分布、多場耦合特性進行仿真計算，用于指導滾動軸承的設計、制造等，以提高軸承性能。

由于滾動軸承接觸區域的位置、大小、形狀及摩擦力分布等在分析前未知，而且會隨著外載荷的變化而改變，因此軸承接觸的動力學分析至關重要[11]。筆者以顯式動力學為基礎，以深溝球軸承6014為例，應用ANSYS/LS-DYNA建立了深溝球三維有限元模型，對軸承在一定速度和載荷下的運轉過程進行了動力學分析，為滾動軸承的工程設計與仿真提供一定參考。

1 顯式動力學分析的基本理論

LS-DYNA中顯式動力學分析采用中心差分方法。將位移函數按泰勒級數展開，得到前后差分公式為：

(1)

(2)

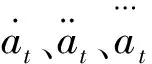
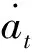
(3)

(4)

軸承系統的動力學求解方程為：

(5)

其中，M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；Qt為節點載荷向量。

將式(3)、(4)代入式(5)，得遞推公式為：

(6)

其中：

(7)

(8)

中心差分法中，只有在時間步長比臨界時間步長小的情況下，顯式分析求解才是穩定的，即：

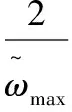
(9)

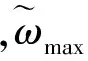
2 滾動軸承有限元模型的建立

2.1 滾動軸承結構尺寸

滾動軸承的結構參數如下[12]：

軸承外徑D110mm

軸承內徑d70mm

軸承寬度B20mm

內圈外徑d282mm

滾球數目 13個

球徑Dw13mm

外圈內徑D298mm

筆者對建模過程進行了適當簡化，如軸承的倒角和邊棱對內部應力影響很小，可以忽略不計。在ANSYS中完成深溝球軸承三維模型的建立。

2.2 單元類型與網格劃分

選用SOLID164單元進行網格劃分，滾動體和內外圈采用六面體單元，保持架由于其結構不規則，采用四面體劃分。由于SOLID164單元不具有旋轉自由度，為了模擬軸承轉動效應，將軸承內圈內表面設定為剛性面，利用SHELL163單元進行劃分，以便施加轉速和載荷。軸承有限元網格劃分如圖1所示，共75 282個節點，91 074個單元。

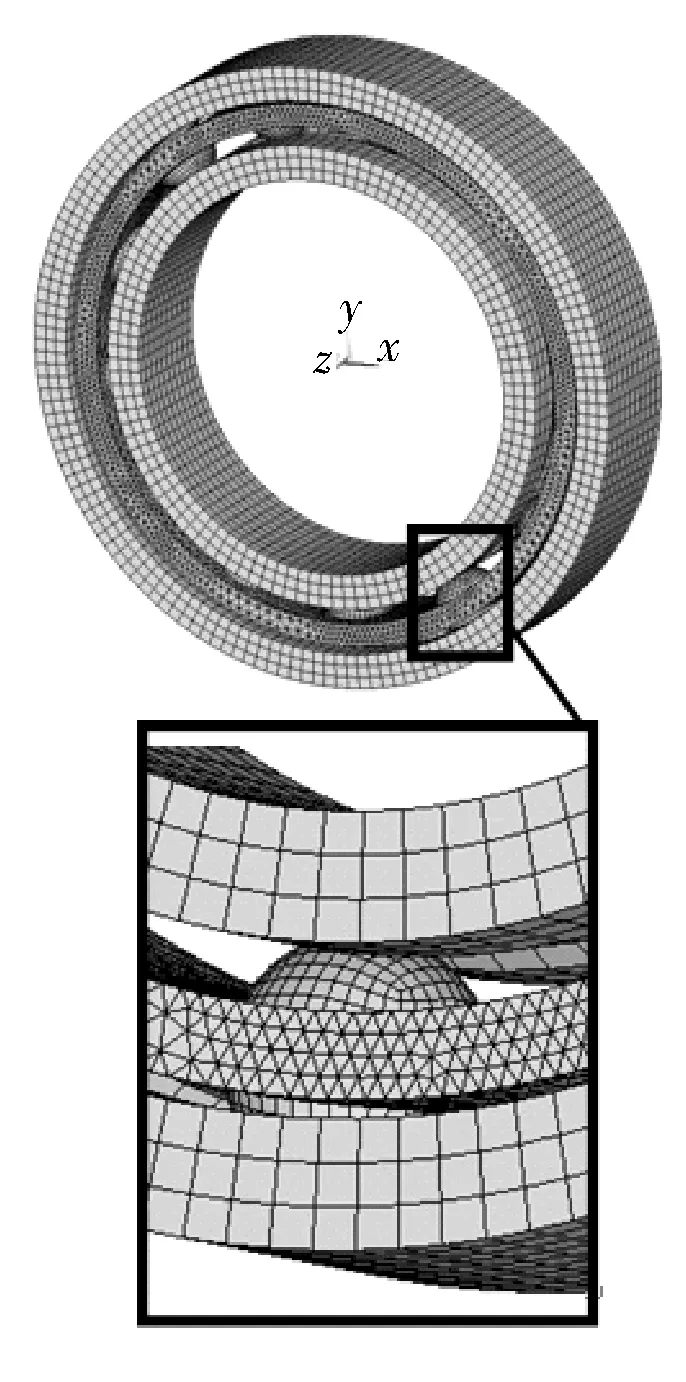
圖1 軸承有限元網格劃分

2.3 材料模型

由于筆者關注的是滾動體和內外圈的受力與變形情況，因此將保持架定義為剛體，計算過程中，剛體內的所有節點的自由度都耦合到其質心上，僅有6個自由度，可以提高計算效率。將滾動體和內外圈定義為彈塑性體，其中內外圈和滾動體的材料均用GCr15鋼，保持架為冷軋鋼板，材料參數為：密度ρ=7830kg/m3，彈性模量E=206GPa，泊松比v=0.3。

2.4 接觸控制與邊界條件

根據實際軸承工作環境，外圈與軸承座緊固，將軸承外圈固定，約束所有自由度，內圈施加徑向載荷和轉速。由于在有保持架的軸承中，滾動體與保持架的短期碰撞會使兩者保持高度動態相互作用，為避免瞬時加速帶來的影響，將轉速在0～5ms內勻速加載。

接觸設置是處理軸承接觸關系的關鍵。由于運動過程中接觸區域具有不確定性，因此，采用自動面面接觸類型。將滾動體與內外圈和保持架分別建立接觸對，假定靜摩擦系數分別為0.35、0.35和0.20，動摩擦系數分別為0.16、0.16和0.10[8,11]。

3 軸承動力接觸仿真分析

3.1 軸承運轉過程動態響應分析

在深溝球軸承運轉時，假定徑向載荷Fr=2kN，轉速為3 850r/min，分析該情況下的動態響應。

根據理論分析，假設溝道接觸處沒有嚴重打滑，則保持架的線速度vm是內圈溝道線速度vi和外圈溝道線速度vo的平均值，滾動體的公轉速度與保持架一致[1]：

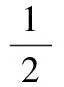
(10)

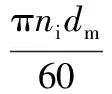
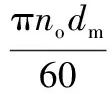
(11)

其中，ni為內圈轉速；dm為節圓直徑；γ為無量綱系數，γ=Dcosa/dm，Dw為球直徑，a為接觸角；no為外圈轉速。

當外圈固定、內圈有轉速時，保持架轉速nm為：

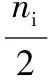
(12)

對于滾動體，除了公轉之外還有自轉。假定內圈溝道和球接觸處沒有嚴重滑動，接觸點上球的線速度與溝道線速度相同，所以：

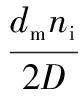
(13)

分別選擇軸承滾動體、內圈和保持架上的某一節點，繪制沿x方向的位移曲線如圖2所示，其中A為滾動體，節點號11 189；B為內圈，節點號5 673；C為保持架，節點號71 968。可以看出，內圈、保持架和滾動體的節點運動都具有周期性的變化規律，內圈做勻速轉動，滾動體公轉的同時自身還有自轉，位移曲線的波峰表示與滾動體外圈接觸的位置。內圈節點位移曲線的一個公轉周期約15.58ms。保持架節點的位移公轉周期為36.80ms。滾動體節點的位移公轉周期為36.20ms，其自轉周期為4.30ms。由式(9)～(13)可以計算得出，保持架的理論周期為36.30ms，滾動體自轉的周期為4.34ms。仿真結果和理論結果是相吻合的。由于保持架存在兜孔間隙，軸承運轉過程中會出現滾動體和保持架打滑的現象，導致滾動體和保持架旋轉周期并不完全相同，這會導致兩者之間發生接觸碰撞。

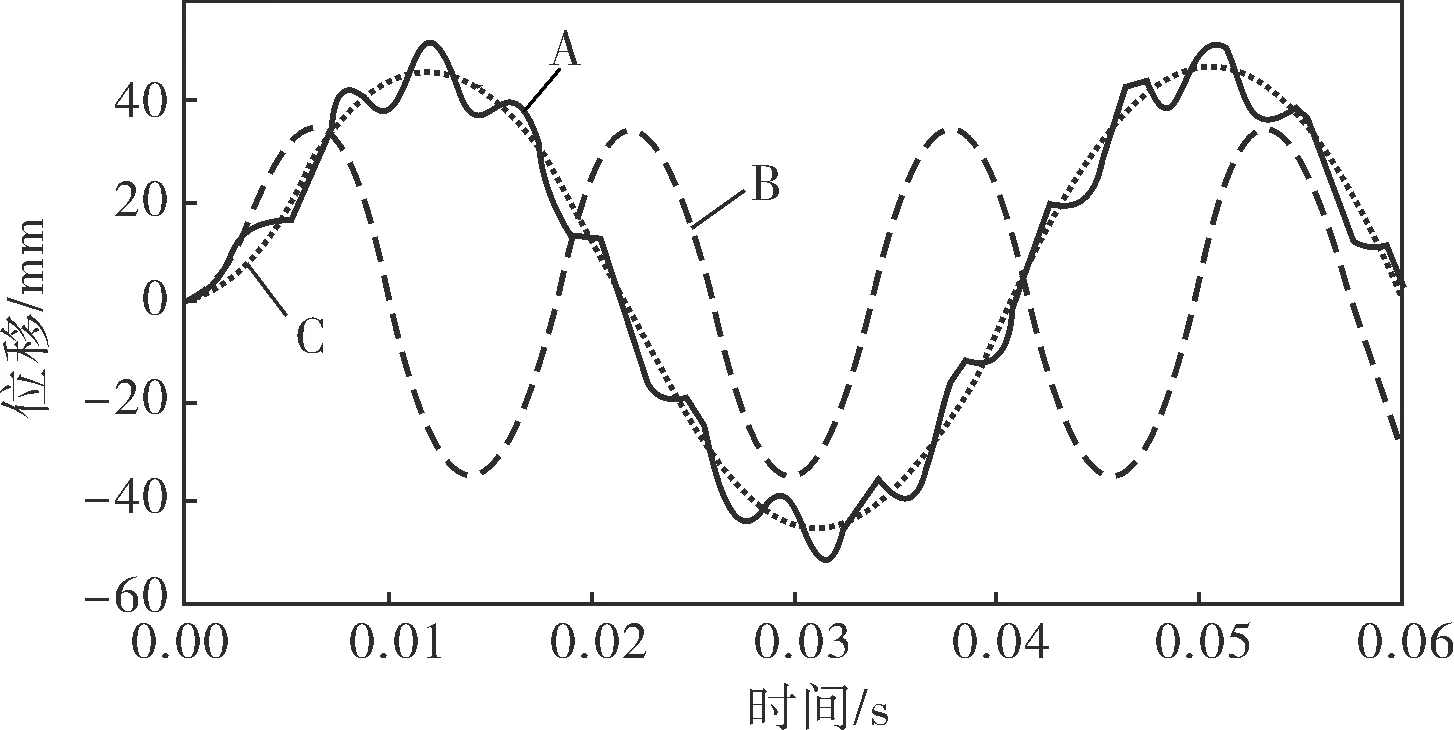
圖2 滾動體、內圈、保持架上某一節點的位移曲線

圖3為滾動體、內圈、保持架節點的速度曲線。可以看出，內圈在0.005s內做加速運動，保持架隨著內圈的加速而加速，在加速過程中，曲線有波動現象，這是由保持架和滾動體的碰撞所導致。加速完成后，保持架和內圈的速度并不是保持不變，而是有微弱變化，這表明即使軸承在正常運轉情況下，也是有振動的。滾動體節點的速度呈現出強烈的變化性，這和圖2中滾動體節點位移曲線的周期性保持一致。

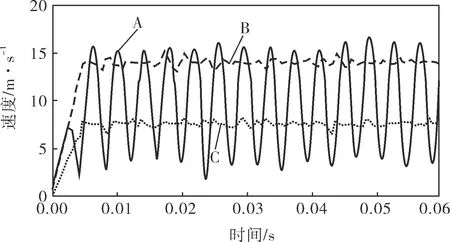
圖3 滾動體、內圈、保持架上某一節點的速度曲線

圖4(D為外圈，節點號3 993)反映了軸承各部分的速度變化有較強的非線性。由于軸承在運轉過程中具有非線性變形，不可避免地會發生振動現象。滾動體的振動最為劇烈，內圈振動較小，保持架次之，外圈振動最小。

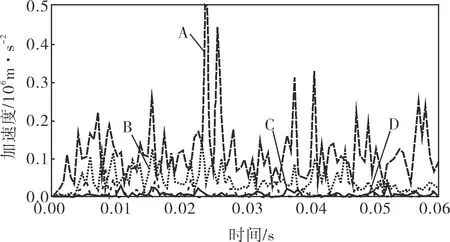
圖4 滾動體、內圈、保持架上某一

3.2 軸承的動態應力分布規律

圖5為軸承在不同時刻的等效應力云圖。滾動體的最大應力出現在滾動體與內外圈的接觸區域。滾動體受力位置和應力最大值在軸承運轉過程中會發生變化。

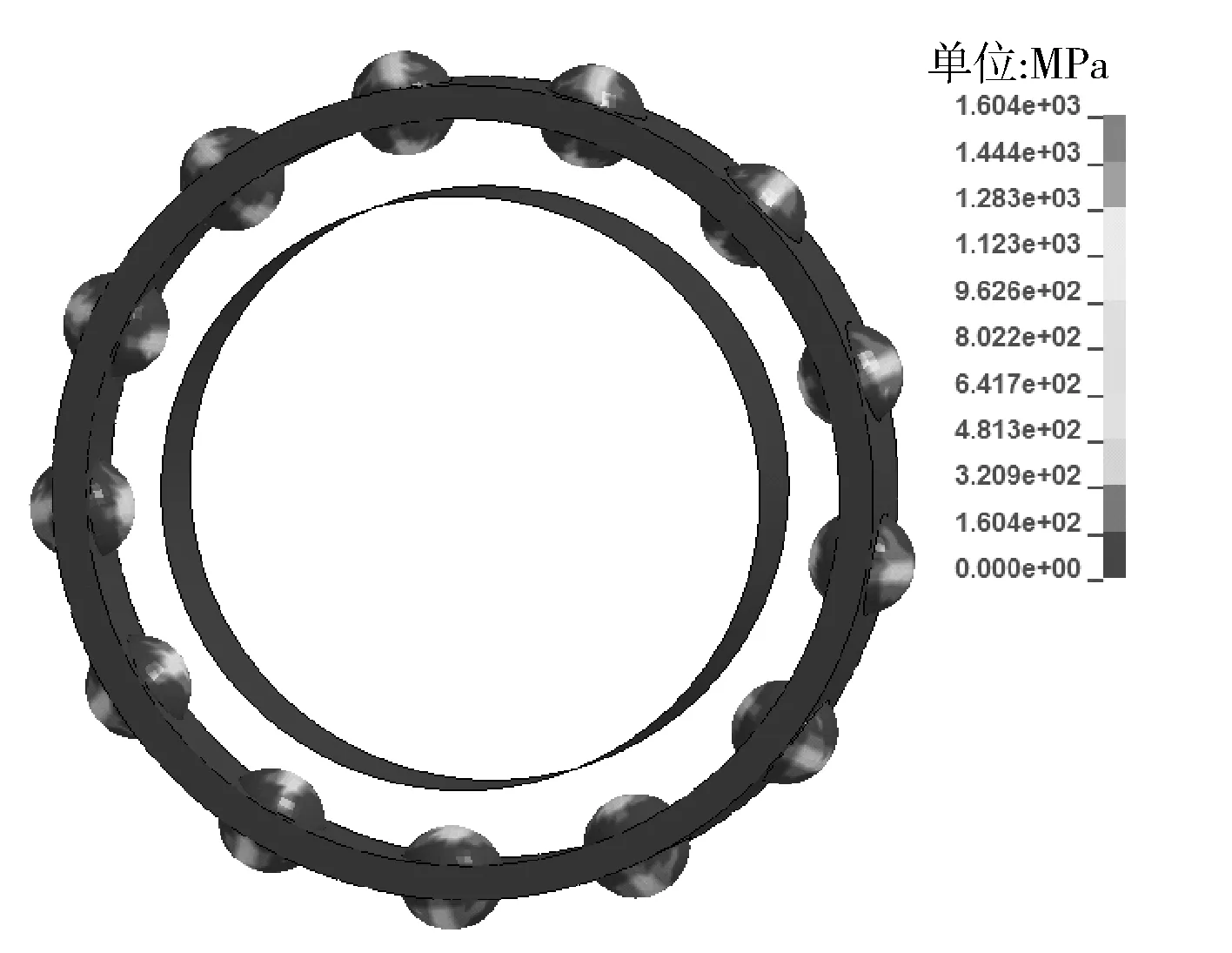
a. t=10.2ms

b. t=20.4ms

圖6為滾動體節點7 552的等效應力曲線。可以看出，由于滾動體在運轉過程中與保持架會有碰撞現象發生，導致滾動體應力波動變化。突然變化的曲線表示單元進入與內外圈接觸的區域。

圖6 滾動體節點7 552的等效應力曲線

圖7為滾動體節點7 552在不同轉速下的等效應力曲線，與圖6對比可以發現，在一定范圍內，轉速的增加會使滾動體最大應力峰值出現的時間提前，但不會使滾動體單元的最大應力值發生顯著變化。

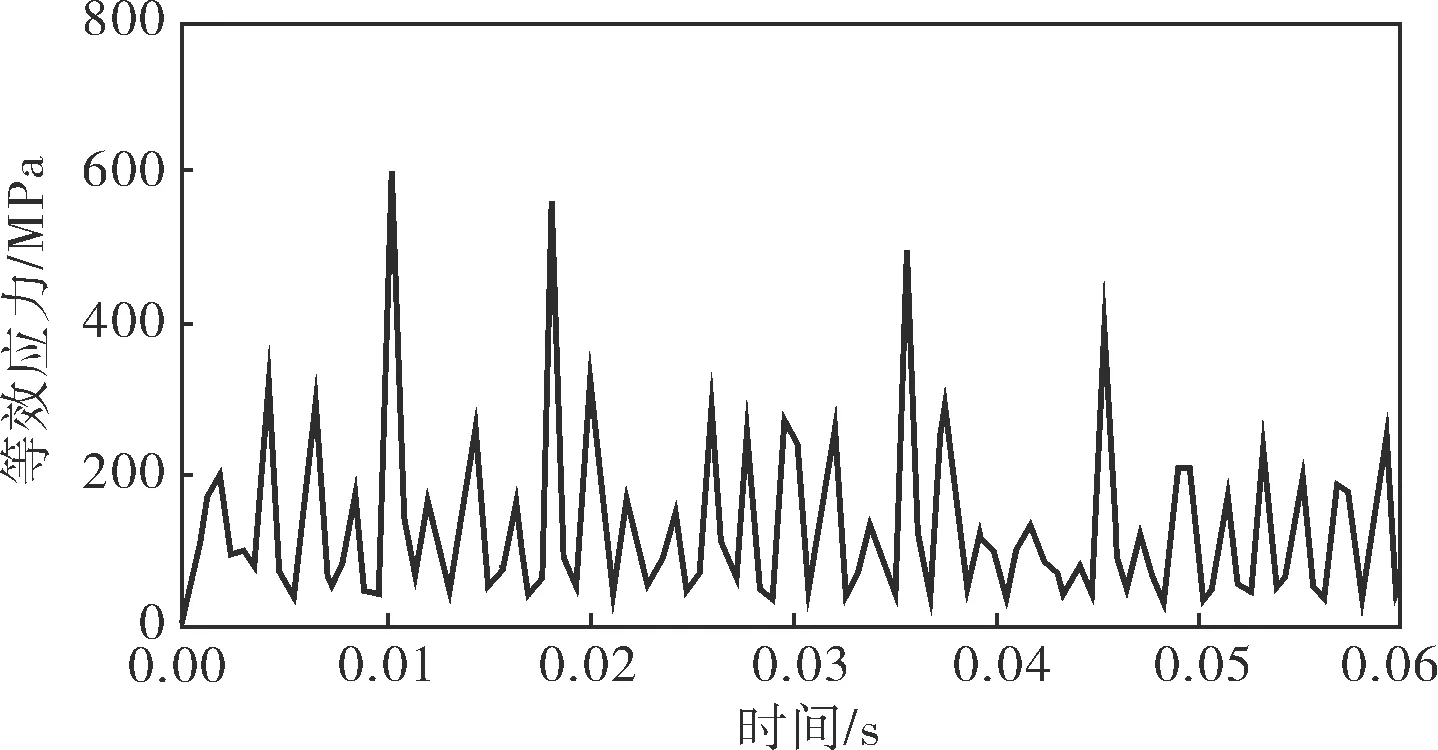
a. 4 500r/min

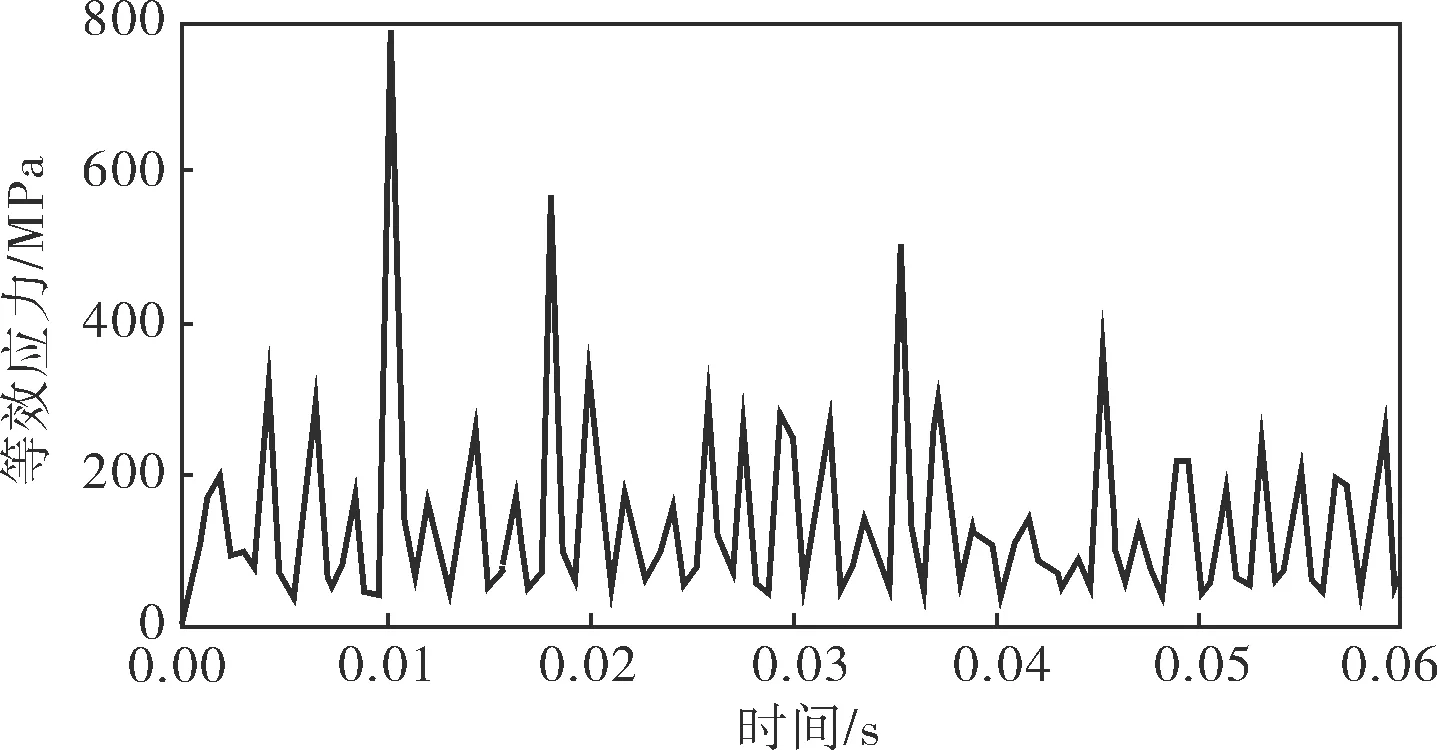
b. 5 800r/min

4 結論

4.1 基于顯式動力學，建立了深溝球軸承有限元力學模型，在轉速和徑向載荷作用下進行了動力學分析。結果表明：滾動體的運動呈周期性變化規律，在每個周期內，滾動體與內外圈的接觸位置有所變化。由于滾動體和保持架旋轉周期并不完全相同，這會引起兩者之間的接觸碰撞。

4.2 軸承在運轉過程中，速度、加速度曲線具有強烈的非線性，不可避免地會發生振動，其中滾動體的振動最為劇烈，內圈、保持架次之，外圈振動最小。

4.3 滾動體的最大應力出現在滾動體與內外圈的接觸區域，軸承運轉過程中，滾動體受力位置發生變化，應力最大值也隨之發生變化。

4.4 在一定轉速范圍內，轉速提高會使滾動體最大應力峰值出現的時間提前，但并不會使滾動體單元的最大應力值發生顯著變化。

[1] Harris T A,Kotzalas M N,著,羅繼偉,譯.滾動軸承分析第2卷:軸承技術的高等概念[M].北京:機械工業出版社,2015:1～10.

[2] 王曉升,屈梁生,趙勃,等.軸承穩定性對懸臂式煙氣輪機振動影響的研究[J].化工機械,1997,24(5):45～49.

[3] 曹瑩,段玉波,劉繼承.基于多尺度的形態濾波降噪方法[J].化工自動化及儀表,2015,42(11):1202～1205.

[4] Lundberg G,Palmgren A.Dynamic Capacity of Rolling Bearings[J].ActaPolytechnica Mechanical Engineering Series,1952,2(4):96～127.

[5] 吳云鵬,張文平,孫立紅.滾動軸承力學模型的研究及其發展趨勢[J].軸承,2004,(7):44～46.

[6] Stone B J.The State of the Art in the Measurement of the Stiffness and Damping of Rolling Element Bearings[J]. CIRP Annals-Manufacturing Technology,1982,31(2):529～538.

[7] Wang J,Kaneta M,Yang P.Numerical Analysis of TEHL Line Contact Problem under Reciprocating Motion[J].Tribology International,2005,38(2):165～178.

[8] 樊莉,譚南林,沈棟平.基于顯式動力學的滾動軸承接觸應力有限元分析[J].北京交通大學學報,2006,30(4):109～112.

[9] 劉旺玉,李靜.基于Hertz理論的深溝球軸承動態接觸分析[J].機械設計與制造,2011,(8):224～226.

[10] 唐云冰,高德平,羅貴火.航空發動機高速滾珠軸承力學特性分析與研究[J].航空動力學報,2006,21(2):354～360.

[11] 林騰蛟,榮崎,李潤方,等.深溝球軸承運轉過程動態特性有限元分析[J].振動與沖擊,2009,28(1):118～122.

[12] Hallquist J O.LS-dyna Keyword User’s Manual Version 970[M].California:Livermore Software Technology Corporation, 2003:818.

MotionProcessNumericalSimulationforDeep-grooveBallBearingsBasedonExplicitDynamics

CHEN Shu-guang, ZHANG Hong-wei, CAI Xiao-jun
(CollegeofMechanicalEngineering,BeijingInstituteofPetrochemicalTechnology)

Basing on explicit dynamics theory and having ANSYS/LS-DYNA adopted, the multi-body contact mechanic model of a 6014 deep-groove ball bearing was established; considering the effects of the speed and load conditions, the dynamic response and contact stress variation of the bearings in motion were analyzed to show that, the simulation result coincides with the result theoretically calculated.

deep-groove ball bearing, explicit dynamics, multi-body contact, finite element model

北京石油化工學院優秀人才培育計劃項目(14031821003-37)；北京石油化工學院科技創新資助項目(15031862005/047)。

陳曙光(1991-)，碩士研究生，從事機械產品現代設計和制造技術的研究。

聯系人張洪偉(1978-)，講師，從事數字化設計與仿真、先進制造技術、機械系統動力學的研究，zhanghw@bipt.edu.cn。

TQ055

A

0254-6094(2017)02-0208-05

2016-02-29，

2016-05-23)