多室魚腹式箱梁剪滯效應分析*

張 海， 金玉佳(沈陽建筑大學 交通工程學院， 沈陽 110168)

多室魚腹式箱梁剪滯效應分析*

張 海， 金玉佳
(沈陽建筑大學 交通工程學院， 沈陽 110168)

針對魚腹式箱梁應力及剪滯效應分布狀態與傳統箱梁不同的問題，通過使用有限元軟件進行模擬分析，研究了魚腹式箱梁在自重荷載作用下的真實受力狀態，分析了引起魚腹式箱梁剪滯系數非常規分布的原因，并為此類箱梁的設計、建設提供了經驗和參考.結果表明，在自重荷載作用下，魚腹式箱梁剪滯效應明顯；腹板的變形平衡條件不同、剪力分配不均、各腹板中性軸變化速率不等是魚腹式箱梁剪滯系數非常規分布的主要原因.

魚腹式箱梁； 有限元； 剪滯系數； 翼板應力； 腹板應力； 腹板撓度； 剪力分配； 中性軸

近些年來，擁有較大抗扭慣性矩、整體性能好以及美觀等眾多優點的魚腹形截面箱梁越來越多地進入了群眾的視野，特別在城市橋梁和快速路高架橋中得到越來越廣泛的應用.曾經備受矚目的箱梁剪力滯后問題在魚腹形箱梁的身上再一次引起人們的關注，特別是魚腹形箱梁的截面端腹板傾斜，橫斷面的端部受力形式類似懸臂，受力復雜不清晰等問題都對剪力滯后效應產生很大的影響.

剪力滯后這一力學現象在結構工程中比較常見[1].翼板上及不同腹板之間的正應力都是通過剪應力來傳遞的，在剪力流作用下，翼板產生剪切變形，從而致使腹板附近的正應力與遠離腹板位置處正應力產生差異，有時這種差異很大，如果忽略會產生嚴重安全后果.由圣維南原理[2]可知，荷載的具體形式只影響荷載作用區域附近的應力分布，隨著荷載作用區域的遠離，這種局部效應影響將變得很小，因而在剪力流的傳遞過程中，隨著腹板的遠離，剪力作用產生的剪切變形將呈現非均勻性，正是這種非均勻性造成結構在彎曲時產生的正應力曲線沿橫向呈現非均勻分布.這種由于剪力流在傳遞過程中存在滯后導致結構的正應力在橫向呈不均勻分布的現象，稱為“剪滯效應”[3-5].在腹板附近考慮剪滯效應時的正應力大于初等梁理論正應力時，稱之為“正剪滯效應”，反之稱為“負剪滯效應”.剪滯系數公式為λ=考慮剪滯效應時的正應力σ/初等梁理論正應力σ′.正剪滯效應時剪滯系數大于1，負剪滯效應時剪滯系數小于1[6-8].

直腹板箱梁剪滯系數在橫向分布與傳統計算方法如能量變分法所得結果相近，然而魚腹式箱梁由于其截面形狀和空間受力等原因將與直腹板箱梁呈現不同的剪滯分布.本文通過使用有限元模擬軟件對魚腹形截面箱梁進行了剪滯效應分析，并對其剪滯系數的具體橫向分布及引起以上分布問題的原因做進一步分析[9-10].

1 模型建立

本文以沈陽市某高架橋為背景，使用通用有限元軟件進行模擬分析.著重探討自重荷載作用下魚腹式箱梁剪滯系數分布問題，箱梁截面尺寸如圖1所示(單位：m).

圖1 截面尺寸Fig.1 Section dimension

橋梁跨徑30 m，橋面寬23.5 m，箱型截面為單箱五室魚腹形截面，C50混凝土彈性模量E=3.45×1010N/m2，泊松比為0.2，容重為2 450 N/m3，模型兩側端部實心截面部分長1 m.為了便于模型計算，簡支邊界條件直接作用于端部底板直線段，網格劃分采用八節點實體單元，全梁總共劃分單元個數為71 164個，有限元網格如圖2所示.

圖2 有限元網格圖Fig.2 Finite element mesh

2 魚腹式箱梁剪滯效應

2.1 剪滯系數分布

通過對上述模型進行計算，得到全橋模型的應力云圖如圖3、4所示.由于該橋的寬跨比較大，結構的受力形式更趨近于板，加之邊腹板傾斜懸臂的結構形式，使結構受力不清晰，模型經過計算后所得結果可以看出該箱梁應力分布并不均勻，上翼板的受力變形形式與板相似，剪滯效應在圖中表現十分明顯.

圖3 頂板正應力云圖Fig.3 Normal stress nephogram of top flange

圖4 底板正應力云圖Fig.4 Normal stress nephogram of bottom flange

使用梁單元建模計算可以得到以平截面假定為基礎的初等梁理論的正應力，按照剪滯系數公式進行計算可得到不同位置截面的剪滯系數分布.為了解上下翼板的剪滯系數分布規律，取距端部2、3、5、7.5和15 m截面作為分析截面，并以橫截面邊緣為參考零點分別取各腹板、翼板中點位參考點對其與初等梁理論計算結果進行對比分析.經計算整理得到該箱梁頂、底板正應力表格及相應的剪滯系數分布曲線，如表1、2和圖5所示.

圖5中，剪滯系數沿橫向分布并不均勻，同一橫斷面不同位置呈現不同的剪滯效應，例如，距離端部2 m處橫截面上出現在2號腹板的剪滯系數已達到1.47，與邊腹板的0.9相差較大.邊腹板(3號腹板)及其懸臂端翼板一直處于負剪滯效應區，腹板之間區域除部分節段的邊腹板與次邊腹板(3號和2號腹板)之間部分區域處于負剪滯效應區外，其余大部分腹板間區域處于正剪滯效應區.距離支座較近時，正剪滯系數最大值出現在次邊腹板與中腹板間翼板上(1號和2號腹板之間)，其最大剪滯系數值為1.47.當所選截面遠離支撐端向跨中靠近時，正剪滯系數值逐漸減小且最大值有向橫斷面中心線靠攏的趨勢，距離端部5 m時最大正剪滯系數值已出現在中腹板(1號腹板)上，此時的剪滯系數最大值已減小為1.19.繼續向跨中靠近過程中，剪滯系數值仍不斷變小，直到跨中位置截面最大剪滯系數減小到其最小值1.08，與此同時，中腹板間翼板上剪滯系數值減小速率明顯小于其他部分，且越遠離橫斷面中心線系數的減小速率越大.在上述變化過程的同時，負剪滯效應也不斷變小，且變化速率逐漸變慢.隨著所選截面遠離支撐端部靠近跨中時，剪滯系數值逐漸趨近于1，在0～L/4附近剪滯系數曲線變化較大，其中，L為計算跨徑，L/4后變化趨同且相對平緩，越靠近跨中位置，截面應力越趨向近似初等梁理論的平截面假定時的應力，但剪滯效應仍很明顯.

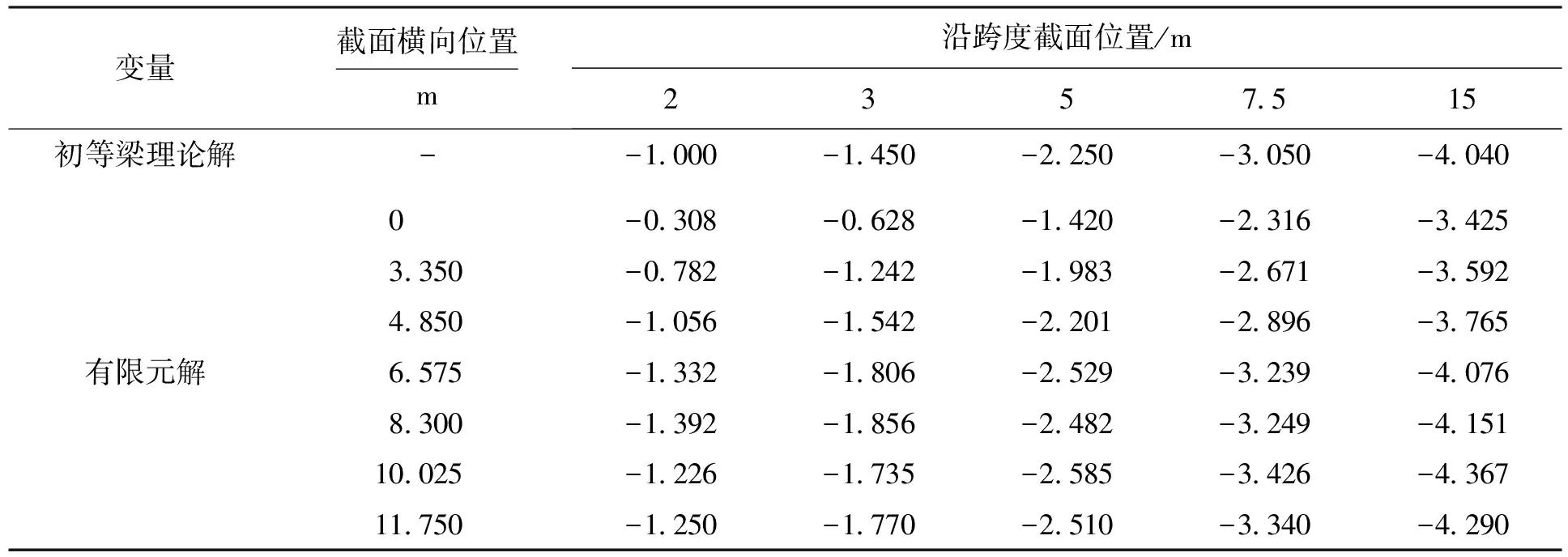
表1 橫截面頂板應力Tab.1 Stress of top flange on cross section MPa

表2 橫截面底板應力Tab.2 Stress of bottom flange on cross section MPa

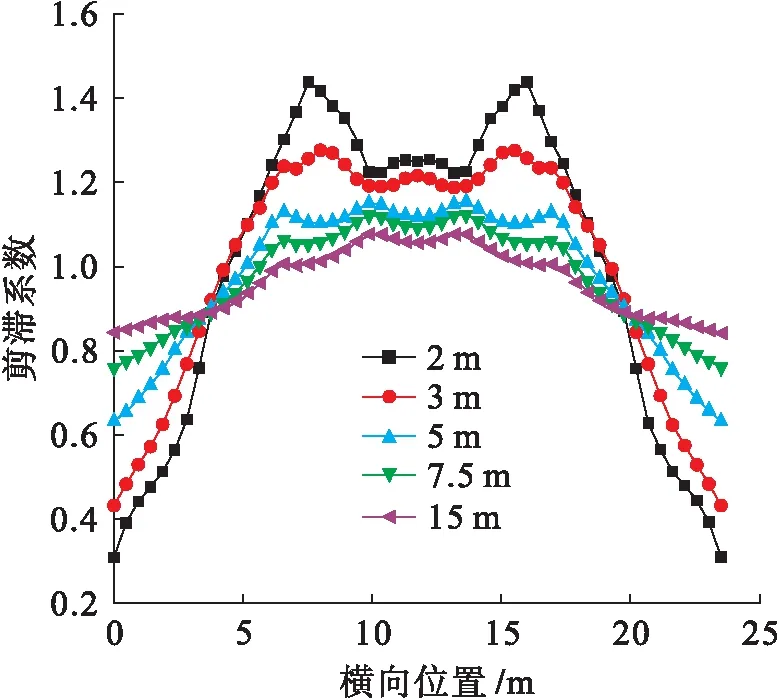
圖5 頂板剪滯系數分布Fig.5 Shear lag coefficient of top flange

圖6為底板剪滯系數分布.底板同樣存在正負剪滯效應分布不均現象，由于邊腹板為魚腹形而且腹板與底板交界不清晰等原因，圖6中各曲線兩端約0.5 m長度不做討論.從圖6可以看出，底板在距離端部支撐附近時，中腹板(1號腹板)間翼板剪滯系數最大且為正剪滯效應，其最大值為1.35.沿中腹板次邊腹板橫向變化，正剪滯效應逐漸減小，負剪滯效應逐漸加大.在0～L/4節段曲線變化較大，L/4至跨中節段橫截面上剪滯系數曲線變化較緩，同時底板完全由負剪滯效應支配，但剪滯系數值與1接近，因此，此時的計算結果與初等梁理論計算結果相差不是很大.

圖6 底板剪滯系數分布Fig.6 Shear lag coefficient of bottom flange

由圖5、6可知，在0～L/4節段最大剪滯系數出現在翼板中部，而L/4至跨中節段剪滯系數的最大值出現在腹板與翼板交接處.因此，在設計計算過程中應注意0～L/4節段的上、下翼板厚度合理過渡及合理布置鋼筋等問題.

2.2 魚腹式箱梁橫向剪滯系數分配

2.2.1 腹板豎向位移及應力

圖7為箱梁豎向位移云圖.根據圣維南原理，距離端部支撐截面較近處截面應力準確值難以正確計算，本文對端部1 m范圍內截面并未加以研究探討.圖8為腹板沿跨度的撓度圖，圖9為腹板沿跨度的正應力圖.由圖8、9可知，魚腹式箱梁整個梁段均存在橫向彎曲，橫向彎曲撓度從支撐端部截面到跨中截面逐漸加大，跨中截面的橫向撓度最大，此時1號與3號腹板在縱向的撓度差值已經達到0.25 mm，而其應力差值已經達到1.4 MPa.魚腹式箱梁上翼板受力變形與帶有加勁肋的板相似，各腹板的作用相當于板上的加勁肋，由于加勁肋的剛度和附加約束作用，板的橫向及豎向變形均有一定影響，同時板的附加約束和附加荷載作用也對腹板的變形產生很大的影響，此時魚腹式箱梁上翼板的變形情況類似板的跨中兩外側邊緣加以集中力的作用.由于該箱梁為整體結構，翼板與腹板無清晰分界，它們之間相互制約，腹板對翼板的板效應有削弱作用，翼板由于橫向位置不同，相應位置處腹板不同的邊界條件(其中包括位移邊界條件和應力邊界條件)致使各腹板的撓度及應力產生很大區別，由圖8、9可以得到不同截面位置處各腹板頂部的位移及正應力的邊界條件.

2.2.2 腹板剪力

圖10為不同位置截面各腹板的剪力曲線圖，可以發現整個箱梁的各個截面一直存在剪力分配不均現象.靠近支撐端部時次邊腹板(2號腹板)的剪力值最大，隨著所選截面在縱向向跨中靠近時，各截面在橫向的最大剪力值不斷向中腹板(1號腹板)靠近，當所選截面在跨中(15 m)時，可以看到中腹板承擔了大部分剪力.魚腹形的邊腹板(3號腹板)在整個過程中所分配到的剪力相對直腹式的次邊腹板和中腹板(2號和1號腹板)要小很多.薄壁結構在對稱荷載作用下彎曲時，不同腹板及翼緣板主要通過剪切變形來傳遞截面的法向正應力，因此，截面上剪力流的分布對該截面的法向應力影響至關重要.圖5、6中截面的剪滯系數沿橫向分布，并非均勻的三次拋物線、正弦曲線等常見剪滯效應分布形式，其最主要原因是由于魚腹形截面剪力分布不均導致同一位置橫截面的不同橫向位置翼板剪切變形不同，且剪切作用使各腹板的中性軸與形心軸發生偏移，各腹板的剪力流分布不同致使各腹板中性軸發生不同程度的偏移，使各腹板的應力產生較大差異，上述原因引起箱梁截面的縱向正應力分布曲線呈現出非均勻的高次拋物線形式.

圖7 箱梁豎向位移云圖Fig.7 Vertical displacement nephogram of box beam

圖8 腹板沿跨度撓度圖Fig.8 Deflection of different webs along span

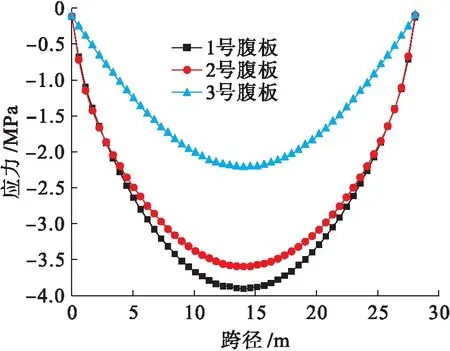
圖9 腹板沿跨度正應力圖Fig.9 Normal stress of different webs along span

圖10 腹板與頂板交接處剪應力Fig.10 Shear stress at junction betweenweb and top flange

2.2.3 中性軸位置

沿箱梁跨度方向位置截面對腹板截面上的應力進行插值計算，可得到各腹板應力零點位置(即中性軸位置)，邊腹板由于其特殊性暫不討論，只對1號腹板、2號腹板進行對比分析.各腹板中應力零點位置如圖11所示.

圖11 腹板應力零點圖Fig.11 Stress zero point curves of webs

由圖11可以看出，1號和2號腹板在端部位置截面和跨中截面的應力零點(中性軸)在豎向并未在同一高度.通過將1(2)和1(15)差值與2(2)和2(15)差值進一步對比分析可以看出，1號腹板的中性軸變化率較2號腹板大.上述分析說明初等梁理論中平截面假定理論不再適用于此類箱梁的設計計算.

3 結 論

此類箱梁截面邊腹板部分的受力形式類似懸臂結構，對主梁的橫向彎曲影響很大，加之邊腹板傾斜，使剪力的分配及傳遞變得復雜，由于此類箱梁截面寬度較寬，截面受力變形趨近于板.綜上在對此類箱梁特別是寬跨比較大的梁橋做設計計算時，已不再適合繼續使用平截面假定為基礎的初等梁理論計算，而應對其進行實體分析計算，應對剪滯效應多加重視.引起橫向彎曲的面內橫向應力及變形、端部至L/4附近截面抗剪強度驗算等問題亦多加考慮不應忽略.

[1] 王繼兵，周德源，秦榮.箱梁剪滯效應分析樣條有限點法 [J].沈陽工業大學學報，2010，32(5)：596-600.

(WANG Ji-bing，ZHOU De-yuan，QIN Rong.Spline finite point method for shear lag analysis of box girder [J].Journal of Shenyang University of Technology，2010，32(5)：596-600.)

[2] Timoshenko S P，Goodier J N.彈性理論 [M].北京：高等教育出版社，2013.

(Timoshenko S P，Goodier J N.Theory of elasticity [M].Beijing：Higher Education Press，2013.)

[3] Zhang Y H.Improved finite-segment method for analyzing shear lag effect in thin-walled box girders [J].Journal of Structural Engineering，2012，138(10)：1279-1284.

[4] 藺鵬臻，劉鳳奎，楊軍，等.箱梁剪滯翹曲位移函數的定義及其應用 [J].計算力學學報，2012，29(5)：789-794.

(LIN Peng-zhen，LIU Feng-kui，YANG Jun，et al.Definition and application of shear-lag warping displacement functions for box girders [J].Chinese Journal of Computational Mechanics，2012，29(5)：789-794.)

[5] 周世軍.箱梁的剪力滯效應分析 [J].工程力學，2008，25(2)：204-208.

(ZHOU Shi-jun.Shear lag analysis of box girders [J].Engineering Mechanics，2008，25(2)：204-208.)

[6] 雒敏，藺鵬臻，孫理想.單箱雙室箱梁的剪力滯效應分析 [J].力學與實踐，2013，35(6)：70-74.

(LUO Min，LIN Peng-zhen，SUN Li-xiang.Analysis of shear lag effect of twin-cell box girders [J].Mechanics in Engineering，2013，35(6)：70-74.)

[7] 張元海.箱形梁橋剪力滯效應及溫度效應理論研究及其應用 [D].成都：西南交通大學，2008.

(ZHANG Yuan-hai.Theory study and application of shear-lag and temperature effect in box-girder bridges [D].Chengdu：Southwest Jiaotong University，2008.)

[8] 郭金瓊，房貞政，鄭振.箱形梁設計理論 [M].北京：人民交通出版社，2008.

(GUO Jin-qiong，FANG Zhen-zheng，ZHENG Zhen.Design theory of box girder [M].Beijing：China Communications Press，2008.)

[9] Song Q，Scordelis A C.Formulas for shear-lag effect of T-，I-，and box beams [J].Journal of Structural Engineering，1990，116(5)：1306-1318.

[10]Luo Q Z，Li Q S，Tang J.Shear lag in box girder bridges [J].Journal of Bridge Engineering，2002，7(5)：308-313.

Shearlageffectanalysisformulti-cellfish-belliedboxbeam

ZHANG Hai, JIN Yu-jia
(School of Traffic Engineering, Shenyang Jianzhu University, Shenyang 110168, China)

In order to solve the problem that the distribution states of stress and shear lag effect of multi-cell fish-bellied box beam are different with those of traditional box beam, the simulation analysis was carried out with finite element software, and the real stress states under the self-weight load effect of fish-bellied box beam were investigated. In addition, the reasons for the un-normal distribution of shear lag coefficient of fish-bellied box beam were analyzed, which could provide the experience and references for the design and construction of the box beams. The results show that under the self-weight load effect, the shear lag effect of fish-bellied box beam is obvious, and the main reasons for the un-normal distribute of shear lag coefficient of fish-bellied box beam are the different deformation balance conditions of webs, different shear distribution and unequal change rate of neutral axis of various webs.

fish-bellied box beam; finite element; shear lag coefficient; flange stress; web stress; web deflection; shear distribution; neutral axis

2016-08-31.

住房和城鄉建設部軟科學研究計劃項目(K42016146).

張 海(1972-)，男，遼寧沈陽人，副教授，博士，主要從事橋梁美學和橋梁振動等方面的研究.

* 本文已于2017-01-19 17∶56在中國知網優先數字出版. 網絡出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20170119.1756.018.html

10.7688/j.issn.1000-1646.2017.06.20

TU 997

A

1000-1646(2017)06-0710-06

(責任編輯：鐘 媛 英文審校：尹淑英)