給定速度需求的移動機器人路徑跟蹤控制與實驗

顧萬里 胡云峰,2 宮 洵 蔡 碩 陳 虹,2

(1.吉林大學通信工程學院，長春 130025； 2.吉林大學汽車仿真與控制國家重點實驗室，長春 130025；3.密歇根大學航空航天工程系，安娜堡 48105)

給定速度需求的移動機器人路徑跟蹤控制與實驗

顧萬里1胡云峰1,2宮 洵3蔡 碩1陳 虹1,2

(1.吉林大學通信工程學院，長春 130025； 2.吉林大學汽車仿真與控制國家重點實驗室，長春 130025；3.密歇根大學航空航天工程系，安娜堡 48105)

針對輪式移動機器人給定速度需求的非連續路徑跟蹤控制問題，將其轉換為滿足速度約束的軌跡規劃和軌跡跟蹤控制。首先，針對給定速度需求的路徑跟蹤問題，以運行時間和能量為優化目標，給定的路徑和速度為約束條件，采用五次Bezier樣條方法優化得到了滿足需求的連續光滑軌跡。其次，利用輪式移動人系統的微分平坦特性，采用微分平坦方法設計前饋控制器；然后，將輪式移動機器人運動學模型在前饋控制的平衡點處進行一階泰勒展開，得到了線性時變的誤差模型，并通過定義新的狀態變量，設計了具有Lyapunov穩定性的誤差反饋控制器。結合前饋控制和反饋控制得到了二自由度軌跡跟蹤控制器。同時將泰勒展開的高階項考慮為有界的擾動輸入，在輸入到狀態穩定性框架下證明了控制系統的魯棒穩定性；最后，通過Pioneer 3-dx輪式移動機器人進行了實驗驗證，實驗結果表明，提出的算法能夠滿足給定速度需求的非連續路徑的跟蹤控制需求。

輪式移動機器人； 路徑跟蹤控制； Bezier樣條； 微分平坦方法； Lyapunov方法

引言

隨著移動機器人在航天[1]、工業[2]、農業[3-5]中的廣泛應用，其軌跡跟蹤問題受到越來越多人的關注。在實際應用中，移動機器人需準確、快速地跟蹤上期望軌跡。但由于輪式移動機器人是一種典型的非完整約束系統，其高精度軌跡跟蹤控制具有一定的難度[6]。

目前，針對非完整移動機器人的路徑跟蹤問題已有很多研究。文獻[7-8]針對連續的期望路徑，設計了基于非線性模型預測控制的路徑跟蹤控制器，該方法能夠有效處理系統的約束，但是上述路徑跟蹤控制方法無法用于離散路徑點跟蹤控制問題；針對路徑點的跟蹤控制問題，主要是將其轉換為軌跡規劃和軌跡跟蹤控制兩部分。對于軌跡規劃問題，早期的研究采用簡單的直線、圓弧及回旋線來生成軌跡曲線，該方法簡單、直觀，但無法保證速度和加速度的連續性[9]。為此，文獻[10-12]采用樣條函數研究軌跡規劃方法，克服了速度和加速度不連續的缺點。但是上述成果中均沒有考慮給定的速度需求。對于軌跡跟蹤控制問題，研究方法主要分成兩方面，一方面是采用非線性控制方法設計控制器，比如滑模控制方法[13-14]、反步法[15]及反饋線性化方法[16]。但該類控制器結構復雜且設計過程繁瑣，由此限制了上述方法的實際應用；另一方面是基于智能控制的軌跡跟蹤控制器設計方法，比如神經網絡方法[17]和迭代學習方法[18]等。該類方法可以在不知精確的機器人系統模型情況下，取得較好的控制效果，但是該算法對控制系統的計算能力要求極高，所以多數停留在仿真階段。

綜上，現有的輪式移動機器人路徑跟蹤控制方法僅是針對路徑需求進行了研究，但是隨著輪式移動機器人應用場景的不斷擴大，不僅對路徑點有要求，也對通過路徑點的速度提出了要求[19]，但目前還鮮有這方面的研究成果。本文針對包含給定速度和位置需求的離散路徑點的輪式移動機器人跟蹤控制問題，設計基于五次Bezier樣條的軌跡規劃方法，以及前饋和反饋相結合的二自由度軌跡跟蹤控制器，并采用Lyapunov方法分析閉環誤差系統的穩定性及魯棒性。

1 問題描述

輪式移動機器人模型如圖1所示。后輪為2個差動驅動輪，前輪為1個起支撐作用的萬向隨動輪。其中，驅動中心和質心重合在P點，(x,y)為機器人的位置坐標，后輪直徑為2r，間距為2b，θ為機器人的位姿角，ω為以垂直軸Z為轉動中心的轉動角速度，v為機器人運動過程中的瞬時線速度。

圖1 輪式移動機器人模型Fig.1 Model of wheeled mobile robot

輪式移動機器人系統為典型的非完整約束系統，其非完整約束包含2個含義：①機器人不能夠側向滑移。②機器人前進時，輪子與地面之間滿足純滾動無滑動的約束條件。輪式移動機器人運動學方程為

(1)

輪式移動機器人給定速度需求的路徑規劃及跟蹤控制問題可以描述為：對于如圖2所示的給定速度需求的路徑點W(x*,y*,v*)，設計路徑跟蹤控制方法使式(1)的實際軌跡能夠通過期望的路徑點(x*,y*)，并且通過該路徑點的速度為v*。為此，本文設計了如圖3所示的控制方案。首先，設計了軌跡規劃算法，根據期望的給定速度需求的路徑點W(x*,y*,v*)生成與時間相關的連續光滑的期望軌跡(xd(t),yd(t))；然后，設計前饋和反饋相結合的二自由度軌跡跟蹤控制器，實現對期望的給定速度需求的路徑點的精確跟蹤控制。

圖2 給定速度需求的期望路徑點Fig.2 Discontinuous path with given velocity requirement

圖3 控制方案Fig.3 Control strategy

2 基于Bezier樣條的軌跡規劃

基于離散的給定速度需求的路徑點P(x*,y*,v*)，生成與時間相關的光滑的軌跡(xd(t),yd(t))。為了讓移動機器人能夠精確跟蹤參考軌跡，生成的軌跡須滿足曲率連續。因此采用五次Bezier樣條曲線對軌跡進行參數化。

假設給定路徑點的個數為n+1，由W{(xi,yi,vi),i=0,1,2,…,n}所示。將任意的相鄰路徑點(Wi,Wi+1)之間的時間歸一化為1 s，則相鄰路徑點(Wi,Wi+1)之間的曲線fi(t)的表達式為

fi(t)=(1-t)5Pi,0+5(1-t)4tPi,1+10(1-t)3t2Pi,2+
10(1-t)2t3Pi,3+5(1-t)t4Pi,4+t5Pi,5

(2)

式中Pi,0、Pi,5——控制軌跡形狀參數

Pi,1、Pi,4——控制軌跡速度參數

Pi,2、Pi,3——控制軌跡加速度參數

針對該參數化軌跡，可以將路徑規劃問題轉換為非線性優化問題，即

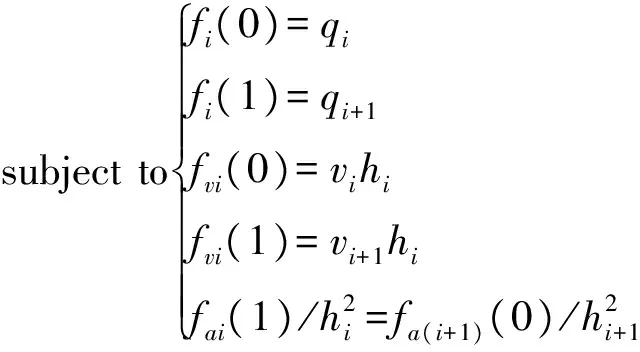
其中

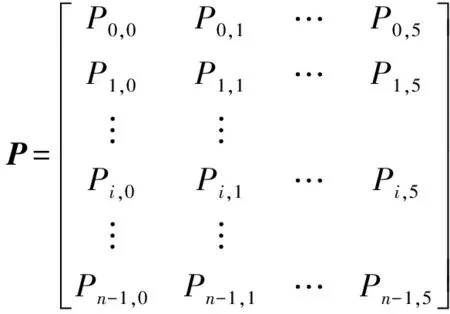
式中f(P,H)——優化目標函數，可以選擇為時間、能量或者沖擊量

P——優化參數H——優化參數

hi——相鄰路徑點間的實際運行時間

fvi(t)——根據軌跡表達式fi(t)求得的速度

fai(t)——根據軌跡表達式fi(t)求得的加速度

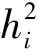
最后，對該非線性優化問題進行求解就可以得到滿足需求的軌跡。該軌跡規劃過程共分為3步：

(1)選擇5次Bezier樣條曲線對軌跡進行參數化，參數分為：控制軌跡形狀的參數P和調節各路徑點之間時間的參數H。

(2)將軌跡規劃問題轉換為非線性優化問題，優化目標函數可以選擇為時間、能量或者沖擊量。約束條件為對應路徑點的位置和速度，且滿足加速度連續條件。

(3)求解該非線性優化問題(如Matlab自帶的fmincon函數)。

3 二自由度軌跡跟蹤控制器設計

3.1 前饋控制器設計

基于微分平坦技術設計了前饋控制器。但在實際過程中，由于系統數學模型不可能完全精確，總會存在不確定性和內外部擾動，在參考軌跡附近，對模型進行線性化，針對得到的誤差模型，設計了反饋控制器，并在Lyapunov穩定性框架下證明了閉環誤差系統的穩定性。

由于輪式移動機器人系統是微分平坦系統[21]，因此，可以通過選取合適的平坦輸出將系統所有的狀態變量和輸入變量用平坦輸出及其有限階導數表示。這里選取平坦輸出

z=(x,y)

(3)

結合輪式移動機器人的運動學模型(1)經簡單推導得

(4)

由于輪式移動機器人系統的狀態和輸入可由平坦輸出及其有限階導數表示，進而可以由期望軌跡(xd(t),yd(t))得到前饋控制率為

(5)

3.2 反饋控制器設計

首先將輪式移動機器人模型在前饋控制的平衡點處進行一階泰勒展開，得到跟蹤誤差系統，進而設計了誤差反饋控制器，并在Lyapunov穩定性框架下證明了閉環系統的穩定性。

定義反饋控制輸入為Δv=v-vf,Δω=ω-ωf，以及系統控制偏差為xe=x-xd,ye=y-yd,θe=θ-θy。將系統(1)在(xd,yd,vf,θf,ωf)點處進行一階泰勒展開得

(6)

式中dx、dy——泰勒展開的高階項，將其考慮成建模誤差

設計控制器的過程中先不考慮建模誤差項，結合式(1)和式(6)，進一步整理可得

(7)

(-vfsinθfxe+vfcosθfye)θe

(8)

由式(8)可知，如果能證明E收斂于0，即可證明xe、ye收斂于0，因此，通過上述變量，將xe、ye2個變量的收斂性問題轉換為一個變量E的收斂性問題。

為了證明誤差系統(7)的穩定性，定義Lyapunov函數

(9)

對式(9)兩端進行求導，并將式(7)、(8)代入可得

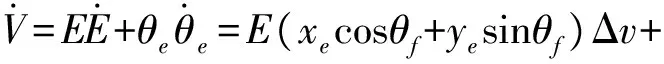
(10)

為了證明誤差系統的穩定性，取

(11)

將式(11)代入式(10)整理可得

(12)

式中k1、k2——控制器參數

由式(12)可知，當選擇k1>0,k2>0時，有

(13)

并且式(13)只在原點處等于零，因此，可以得到E、θe可以漸進收斂于0，即可得到xe、ye、θe收斂于0。

上述過程證明了在忽略系統建模誤差時，閉環誤差系統具有漸進穩定性，但是系統中存在泰勒展開的高階項等建模誤差，因此，需要進一步證明，閉環系統存在擾動情況下的魯棒穩定性。

3.3 魯棒穩定性分析

在以上控制器設計過程中，由于未考慮建模誤差，本節將建模誤差考慮成幅值有界的擾動，在輸入到狀態穩定性理論框架下，證明了閉環誤差系統的魯棒性。

包含建模誤差的誤差動力學方程為

(14)

為了證明其閉環系統的魯棒性，本文將包含建模誤差的式(14)代入到式(9)定義的Lyapunov函數導數方程中，得到

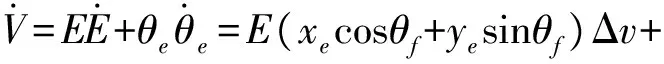
(15)

將控制輸入式(11)代入到式(15)，得到

(16)

為此，對式(16)右端使用Young’s不等式可得

因此，由輸入到狀態穩定性理論可知，系統從擾動輸入dx、dy到狀態E、θe具有穩定性，即具有魯棒穩定性。

4 實驗與分析

圖4 Pioneer 3-dx實物圖Fig.4 Photo of Pioneer 3-dx

為了驗證本文所提出的算法有效性，在Mobilerobots公司開發的Pioneer 3-dx實驗平臺上對該算法進行了實驗驗證。該平臺實物如圖4所示。Pioneer 3-dx機器人以客戶端—服務器模式運行。客戶端采用PC實現，用于運行Windows程序和基于C++編寫的用戶應用程序。服務器端基于DSP實現，用于執行移動機器人底層控制，包括速度控制及采集傳感器信息。客戶端和服務器端采用串口進行通訊。該移動機器人主要參數如表1所示。

表1 Pioneer 3-dx機器人參數Tab.1 Parameters of Pioneer 3-dx

在實驗過程中，首先基于Pioneer 3-dx機器人PC客戶端運行的Matlab軟件編寫了軌跡規劃程序，對于步驟3中的優化函數選擇為fmincon函數，由此得到了期望的運行軌跡。然后，基于Mobilerobots公司開發的ARIA控制接口庫，在VS2010編譯器下采用C++編寫了軌跡跟蹤控制程序。

針對本文所設計算法，給出以下兩種路徑用于進行實驗驗證。

(1) 路徑點的跟蹤控制

以路徑點W0=[(0,0,0.18);(0.6,0.1,0.30); (1.8,0.6,0.50); (3.0,0.9,0.60); (5.0,1.0,0.30); (5.8,0.6,0.10)]和W1=[(0,0,0.18); (0.6,0.1,0.30); (1.5,0.5,0.50); (2.6,1.5,0.60); (3.9,3.5,0.50); (5.0,6.0,0.10)]為例，來驗證本文算法的有效性。

對于路徑點的跟蹤控制，首先需要進行軌跡規劃，采用前文基于Bezier樣條的軌跡規劃方法進行軌跡規劃，對于得到的期望軌跡，其Bezier樣條參數如下：

針對路徑點W0規劃得到的軌跡，對應的五次Bezier樣條曲線的參數為

針對路徑點W1規劃得到的軌跡，對應的五次Bezier樣條曲線的參數為

由此得到規劃的參考軌跡和期望的路徑及速度對比曲線如圖5～8所示。

圖5 路徑點W0規劃得到的x和y方向軌跡Fig.5 Generated reference trajectories for waypoints W0 in x and y directions

圖6 路徑點W0規劃路徑和速度與參考值對比Fig.6 Comparison of generated reference trajectory and reference value for waypoints W0

由圖5～8可看出，采用該方法規劃得到的軌跡能夠精確經過期望的路徑點。

以圖5和圖7中的軌跡作為跟蹤實驗的參考軌跡，采用推導的軌跡跟蹤算法進行軌跡跟蹤實驗，對于路徑點W0初對應的始偏差分別選擇為(0,0,0)和(0.6,0.3,0)。對于路徑點W1初對應的始偏差分別選擇為(0,0,0)和(1.0,1.0,0)。其實驗結果如圖9～12所示。

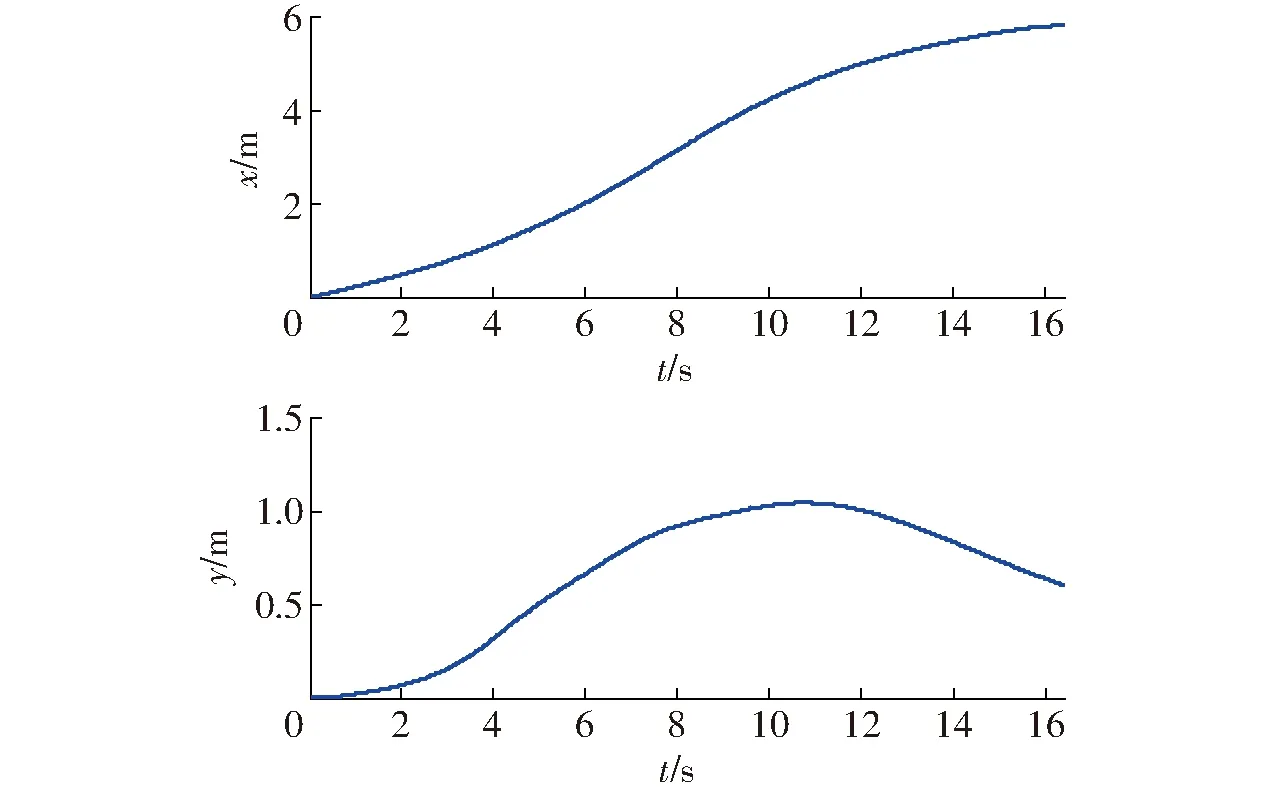
圖7 路徑點W1規劃得到的x和y方向軌跡Fig.7 Generated reference trajectories for waypoints W1 in x and y directions

圖8 路徑點W1規劃路徑和速度與參考值對比Fig.8 Comparison of generated reference trajectory and reference value for waypoints W1

圖9 路徑點W0跟蹤誤差Fig.9 Tracking errors for waypoints W0

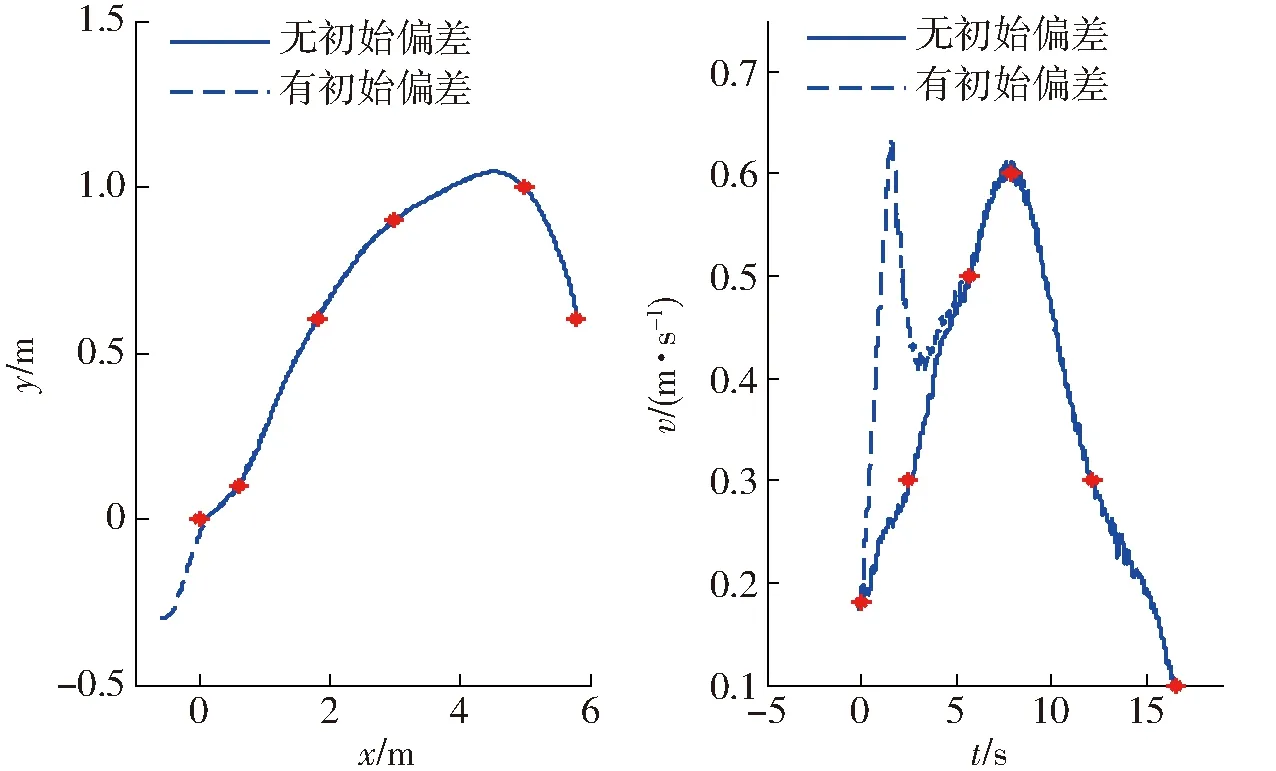
圖10 路徑點W0實際路徑和速度與參考值對比Fig.10 Comparison of real path and velocity with reference value for waypoints W0

由圖9～12可得，在沒有初始偏差情況下，該控制器能夠很好跟蹤上期望軌跡。在有初始偏差情況下，該控制器能夠很快收斂到期望軌跡。

圖11 路徑點W1跟蹤誤差Fig.11 Tracking errors for waypoints W1

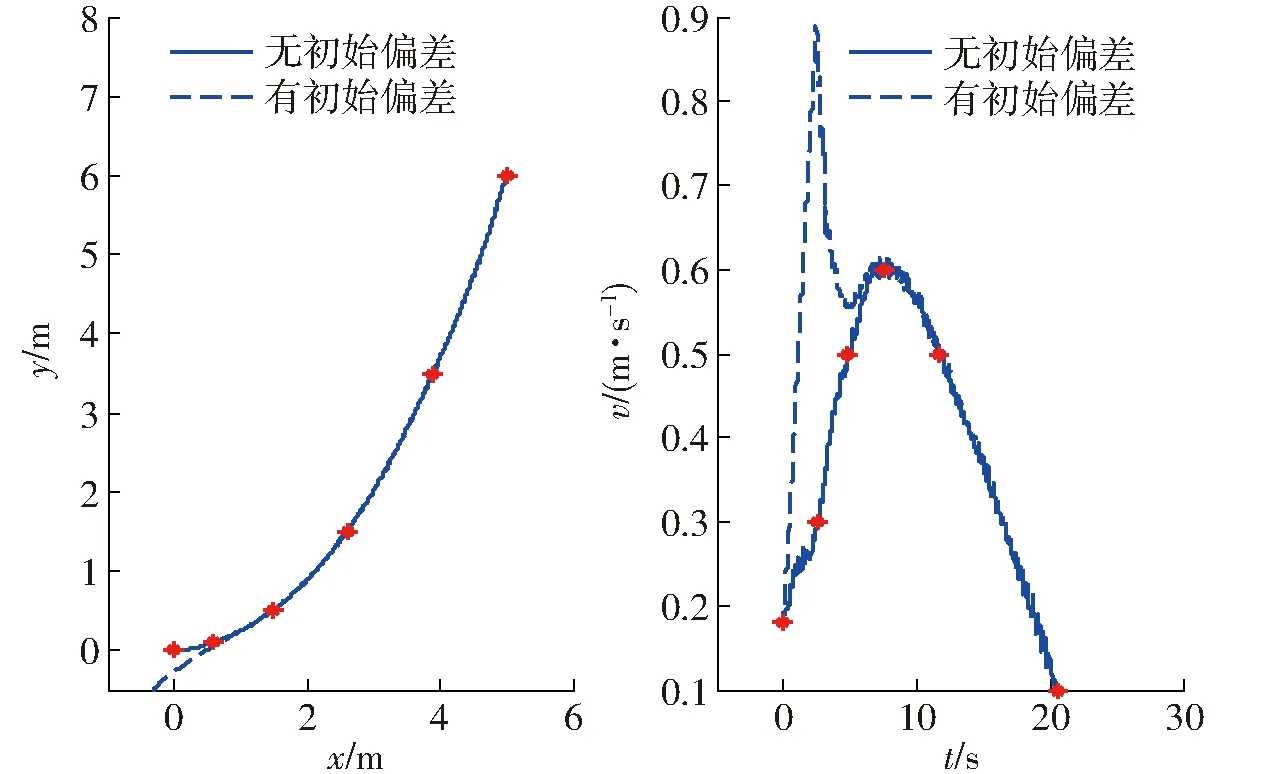
圖12 路徑點W1實際路徑和速度與參考值對比Fig.12 Comparison of real path and velocity with reference value for waypoints W1

(2) 圓軌跡跟蹤控制

其參考軌跡為

采用推導的軌跡跟蹤算法進行軌跡跟蹤實驗，初始偏差分別選擇為(0,0,0)和(0.6,0.6,0)。其實驗結果如圖13、圖14所示。

圖13 跟蹤誤差Fig.13 Tracking errors

由圖13、圖14可以得到，在沒有初始偏差情況下，該控制器能夠很好跟蹤上期望的軌跡。在有初始偏差情況下，該控制器能夠很快收斂到期望的軌跡。

5 結束語

研究了給定速度需求的路徑點跟蹤控制問題。首先,設計了能夠滿足速度需求的基于Bezier樣條優化的軌跡規劃方法。針對規劃得到的軌跡，設計了具有前饋和反饋結構的軌跡跟蹤控制器，對其進行跟蹤控制。結果表明，本文設計的軌跡規劃方法能夠滿足精確的速度需求，且設計的軌跡跟蹤控制器可以使系統跟蹤上該軌跡，從而完成了整個運動控制。

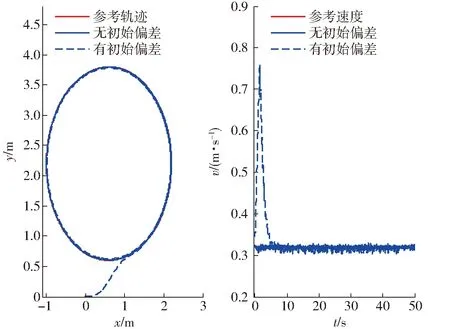
圖14 實際路徑和速度與參考值對比Fig.14 Comparison of real path and velocity with reference value

1 SUTOH M, OTSUKI M, WAKABAYASHI S, et al.The right path: comprehensive path planning for lunar exploration rovers [J].IEEE Robotics & Automation Magazine, 2015, 22(1): 22-33.

2 CEN Y, SONG C, XIE N, et al.Path planning method for mobile robot based on ant colony optimization algorithm[C]∥3rd IEEE Conference on Industrial Electronics and Applications.ICIEA, Iciea, 2008: 298-301.

3 趙源深, 貢亮, 周斌,等.番茄采摘機器人非顏色編碼化目標識別算法研究[J/OL].農業機械學報, 2016, 47(7):1-7.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160701&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.07.001.

ZHAO Yuanshen, GONG Liang, ZHOU Bin, et al.Object recognition algorithm of tomato harvesting robot using non-color coding approach [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7):1-7.(in Chinese)

4 錢曉明, 張浩, 王曉勇,等.基于激光掃描匹配的移動機器人相對定位技術研究[J/OL].農業機械學報, 2016, 47(3):14-21.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160303&journal_id=jcsam.DOI:10.6041/ j.issn.1000-1298.2016.03.003.

QIAN Xiaoming, ZHANG Hao, WANG Xiaoyong, et al.Relative localization technology for mobile robot based on laser scan matching [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3):14-21.(in Chinese)

5 褚佳, 張立博, 張鐵中,等.葫蘆科穴盤苗單人操作嫁接機器人設計與試驗[J/OL].農業機械學報, 2017,48(1):7-13.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170102&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2017.01.002.

CHU Jia, ZHANG Libo, ZHANG Tiezhong, et al.Design and experiment of grafting robot operated by one person for cucurbitaceous seedlings cultivated in plug trays[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2017,48(1):7-13.(in Chinese)

6 BOMG S P, SUNG J Y, JIN B P, et al.A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots [J].IEEE Transactions on Control Systems Technology, 2010, 18(5): 1199-1206.

7 YU S, LI X, CHEN H.Nonlinear model predictive control for path following problems [J].International Journal of Robust and Nonlinear Control, 2015, 25(8): 1168-1182.

8 劉洋.基于模型預測控制的移動機器人路徑跟蹤控制[D].長春：吉林大學,2016.

LIU Yang.Nonlinear model predictive control for path-following problems of wheeled mobile robots [D].Changchun:Jilin University, 2016.(in Chinese)

9 KOMORIYA K, TANIE K.Trajectory design and control of a wheel-type mobile robot using B-spline curve[C]∥Intelligent Robots and Systems’89.The Autonomous Mobile Robots and Its Applications.IROS’89.Proceedings, IEEE/RSJ International Workshop on IEEE, 1989: 398-405.

10 GASPARETTO A, ZANOTTO V.Optimal trajectory planning for industrial robots[J].Advances in Engineering Software, 2010, 41(4): 548-556.

11 KUCUK S.Maximal dexterous trajectory generation and cubic spline optimization for fully planar parallel manipulators[J].Computers & Electrical Engineering, 2016, 56: 634-647.

12 BHARATHI A, DONG J.Feedrate optimization for smooth minimum-time trajectory generation with higher order constraints[J].The International Journal of Advanced Manufacturing Technology, 2016, 82(5-8): 1029-1040.

13 QIAN D, TONG S, LI C.Leader-following formation control of multiple robots with uncertainties through sliding mode and nonlinear disturbance observer[J].ETRI Journal, 2016, 38(5): 1008-1018.

14 QIAN D, LI C, TONG S, et al.Integral sliding mode-based formation control of multiple unertain robots via nonlinear disturbane observer[J].International Journal of Advanced Robotic Systems, 2016, 13(6): 1-11.

15 CHWA D.Robust distance-based tracking control of wheeled mobile robots using vision sensors in the presence of kinematic disturbances[J].IEEE Transactions on Industrial Electronics, 2016, 63(10):6172-6183.

16 LUVIANO-JUREZ A, CORTS-ROMERO J, SIRA-RAMREZ H.Trajectory tracking control of a mobile robot through a flatness-based exact feedforward linearization scheme[J].Journal of Dynamic Systems, Measurement, 2015, 137(5): 051001.

17 YE J.Tracking control of a non-holonomic wheeled mobile robots using improved compound cosine function neural networks [J].International Journal of Control, 2015, 88(2): 364-373.

18 LU X, FEI J.Velocity tracking control of wheeled mobile robots by iterative learning control [J].International Journal of Advanced Robotic Systems, 2016, DOI: 10.5772/63813.

19 孫施浩,趙林,賈英民.空間合作目標運動再現的相似設計方法研究[J].宇航學報, 2014, 35(7): 802-810.

SUN Shihao, ZHAO Lin, JIA Yingmin.Similitude design method for motion reconstruction of space cooperative vehicles [J].Journal of Astronautics, 2014, 35(7): 802-810.(in Chinese)

20 余伶俐, 龍子威, 周開軍.基于貝塞爾曲線的機器人非時間軌跡跟蹤方法[J].儀器儀表學報, 2016, 37(7): 1564-1572.

YU Lingli, LONG Ziwei, ZHOU Kaijun.Non-time trajectory tracking method based on Bezier curve for robot[J].Chinese Journal of Scientific Instrument, 2016,37(7):1564-1572.(in Chinese)

21 WALSH G, TILBURY D, SASTRY S, et al.Stabilization of trajectories for systems with nonholonomic constraints [J].IEEE Transactions on Automatic Control, 1994, 39 (1): 216-222.

PathTrackingControlandExperimentsforWheeledMobileRobotswithGivenVelocityRequirement

GU Wanli1HU Yunfeng1,2GONG Xun3CAI Shuo1CHEN Hong1,2

(1.CollegeofControlScienceandEngineering,JilinUniversity,Changchun130025,China2.StateKeyLaboratoryofAutomotiveSimulationandControl,JilinUniversity,Changchun130025,China3.DepartmentofAerospaceEngineering,MichiganUniversity,AnnArborMI48105,USA)

For the discontinuous path tracking problem of wheeled mobile robots with given velocity requirement, it was transformed into the trajectory planning and trajectory tracking problems.Firstly, for the given position and velocity requirements, quintic Bezier curve was used to parameterize the trajectory.Then the trajectory planning problem was transformed into the nonlinear optimization problem, for which the energy and interval times were selected as the optimization objective to optimize the parameterized trajectory.By solving the nonlinear optimization problems, a continuous and smooth trajectory was generated, which satisfied the given position and velocity requirements.Secondly, by exploiting the differential flatness properties of the wheeled mobile robots system, a feedforward controller was designed by using the differential-flatness approach.Thirdly, the kinematic model of the wheeled mobile robots was linearized at its equilibrium point of the feedforward control by using the first order Taylor expansion.Then, an linear time-varying error model was deduced.By defining a new error variable, a feedback controller was designed and the stability of closed loop error system was proved in the Lyapunov framework.Therefore, a two degree of freedom trajectory tracking controller was given.This method had the advantages of simple structure and clear engineering significance.In addition, the higher order terms of the Taylor series were considered as a bounded disturbance input, and the robustness of the system was discussed in the framework of input to state stability theory.Finally, the effectiveness of the proposed trajectory planning and trajectory tracking methods was validated on the Pioneer 3-dx wheeled mobile robot experiment platform.It can be seen from the experimental results that the proposed methods can track the discontinuous path with the given velocity requirement precisely.

wheeled mobile robot; path tracking control; Bezier curve; differential-flatness approach; Lyapunov method

10.6041/j.issn.1000-1298.2017.10.003

TP273

A

1000-1298(2017)10-0025-07

2017-05-18

2017-07-21

國家自然科學基金重點項目(61520106008、61374046)

顧萬里(1988—)，男，博士生，主要從事非線性控制系統設計研究,E-mail: guwl13@mails.jlu.edu.cn

胡云峰(1983—)，男，副教授，主要從事非線性控制應用及汽車電子控制研究,E-mail: huyf@jlu.edu.cn