考慮組合分散化效應的股票質押定價分析

（上海交通大學安泰經濟與管理學院, 上海 200030）

引言

股票質押業務目前在我國迅速發展，據Wind統計，2016年滬深兩市共有53%的上市公司進行股票質押，股數達3067.64億，涉及市值4.15萬億元，分別較2015年高出94.65%和46.13%。隨股票質押業務迅猛發展，股票質押率定價的重要性開始凸顯，它直接影響質權人的收益能否與風險合理匹配：若質押率過高，雖可提高對質押人的吸引力，從而助力業務規模擴張，但質權人融出的資金也往往會超出合理范圍，致使其收益難以覆蓋風險；若質押率過低，雖然風險很低，但這往往會削弱質權人的市場吸引力，導致業務規模被壓縮。

關于股票質押率定價，在股票質押業務實踐中，雖然業務框架已具備，但實踐中的股票質押率定價方法嚴重落后于理論，而現有的理論定價方法也存在諸多缺陷。目前，理論界多是簡單依據波動率風險來對單一股票標的進行定價，VaR(Value at Risk，在險值)方法被廣泛用于股票質押率定價，其基本思想為：質權人參考一段時期的股票價格變化，在特定置信水平下估算質押期內股票的最大損失，進而轉化為質押率以覆蓋股票的價格風險。例如，王志誠等(2002)[17]基于滬深兩市所有A股股票1995～2000年的數據，利用VaR風險測度方法來給出股票質押率；再如于輝等(2010)[20]、何娟等(2012)[10]，均是利用VaR方法確定質押率。但VaR只是度量在一定置信水平下的最大損失，它無法估計超出最大損失之外的超額損失，即它忽視了質押標的尾部損失，據其算得的折算率往往高估。因此，學界對基于VaR的質押率定價方法進行了改進：一是用CVaR(Conditional VaR，條件在限制)、ES(Expected Shortfall，預期不足)等測度代替VaR，以彌補VaR測度無法描述分位數之外損失的缺陷，如何娟等(2015)[11]在CVaR框架下，引入改進的均值方差優化技術，對質押率進行研究；二是VaR測度與GARCH模型結合，通過GARCH模型刻畫的波動聚集來估計質押標的的尾部損失，如董珊珊(2012)[9]、李虹等(2016)[14]均提出利用GARCH模型測算股票質押率。

上述研究為本文提供了寶貴的理論借鑒，但精確度和實用性還明顯不足，體現在以下兩方面：

第一、現有股票質押率定價忽視了組合視角下的研究方法，即忽視了組合分散化效應對質押率定價的影響。在實際股票質押業務中，質權人更可能持有的是多只質押股票的組合(即一個質權人事實上會對應多位質押人，而質押人所質押的股票又不一樣)。在傳統股票質押率定價中(即質權人并非基于組合視角進行質押率定價)，質權人只是單獨對每只股票進行質押率定價，而不考慮質押股票之間的相互關系。然而，根據Markowitz(1952)[8]或者說組合風險分散效應，質權人所持的質押股票組合的風險并不是單一股票風險的簡單相加，此時，質權人整體質押業務風險不應是各質押股票所含風險的加權平均。因此，為實現質權人整體質押業務的風險--收益平衡，質權人必須基于組合視角進行質押率定價，即根據質押股票對質權人的風險貢獻進行質押率定價。只有對組合風險進行分解，使之能夠描述各質押股票對質權人總體風險的貢獻大小，才能在此基礎上得到合理的質押率。

第二、當以組合視角分析質押業務時，傳統VaR方法并非理想的質押率定價方法。一方面，股票之間往往呈現非線性相關關系，基于線性相關系數的VaR方法難以準確地得到組合風險價值；另一方面，股票收益率多呈現尖峰厚尾、波動聚集等特征，組合收益率并不服從常見的多元正態分布。要準確計算組合VaR，必須準確地刻畫各股票的邊緣分布以及股票之間的相依結構。解決這一問題的方法之一就是Copula方法，Copula函數可將標的股票的邊際分布與它們之間的相依結構分開研究，且股票的邊緣分布選擇不受限制，此時即可用GARCH模型刻畫股票收益率的尖峰厚尾、波動聚集特征，其實用性和效率更高。但是多元Copula在刻畫多資產相依結構及度量組合VaR等問題上存在缺陷：多元Copula函數假定金融資產間的相依結構必須用同一類Copula刻畫，不允許組合中不同資產之間存在不同的相依結構，而在真實的金融市場中，金融資產間的相依結構并非完全一致(即組合中不同資產之間可能存在不同的相依結構)。為解決這一問題，Joe(1996)[7]提出了基于Pair Copula構造多維Copula模型的方法，Bedford and Cooke(2001,2002)[1][2]在Joe(1996)[7]基礎上，進一步引入了稱之為藤(Vine) Copula的相依結構。Vine Copula理論利用Pair Copula作為基礎模塊來建立多維Copula模型，它允許不同隨機變量之間存在不同的Copula相依結構，較多元Copula，Vine Copula在刻畫多維隨機變量間的相依結構上具有更強的靈活性和實用性。目前，Vine Copula已廣泛應用于多元數據建模，例如Heinen and Valdesogo(2009)[6]運用C-vine建立了多只股票收益率之間的動態相依結構模型；李磊等(2013)[15]基于C-vine Copula估計了相應投資組合的CVaR；居姍等(2013)[13]基于D-vine Copula給出了多資產投資組合的VaR估計方法。但值得強調的是，Bedford and Cooke(2001, 2002)[1][2]提出Regular Vine Copula(簡記為R-vine Copula)，較C-vine和D-vine(C-vine和D-vine僅是R-vine的特殊結構，C-vine呈星型結構，D-vine呈平行結構)更適于有效預測組合VaR，如吳海龍等(2013)[18]、馬鋒等(2015)[16]的實證研究均表明R-vine Copula對投資組合VaR的預測效果最好。

基于上述認識，本文開展以下研究工作：首先將單一股票質押問題擴展至組合質押視角，利用AR(1)-GARCH(1, 1)模型分析各股票收益率的邊緣分布，以刻畫收益率分布的尖峰厚尾、波動聚集等典型分布特性；其次，在刻畫邊緣分布的基礎上，采用R-vine Copula模型對多元數據進行建模，得到任意n只股票收益率的聯合分布和相依結構；最后結合Monte Carlo模擬方法，利用Copula-GARCH的組合VaR分解技術得到各質押股票對應的成分VaR以反映其風險貢獻，進一步得到其相應的質押率，并與基于傳統VaR情形的質押率定價進行對比驗證。

基于R-vine Copula-GARCH的質押率定價模型

本文把單一股票質押問題擴展至組合質押視角，以考慮質權人組合分散化效應對質押率定價的影響，目的在于提高質押業務整體風險--收益平衡性。傳統上，即使質權人持有多只質押股票，質權人也只是單獨對每只股票進行質押率定價，而不考慮質押標的之間的相依結構；而在基于質權人視角的質押問題中，質權人會將其所有質押股票看作一個投資組合來考慮風險，然后根據質押股票的風險貢獻進行質押率定價。

質押率反映的是質押標的的預期損失被覆蓋后，質權人融出資金占質押標的期初價值之比。基于傳統VaR方法的質押率β可表示如下：

其中，VaR表示一定顯著性水平下的VaR值；顯著性水平通常等于0.01，即質權人據此設定質押率后，面臨損失的概率為1%。

在傳統定價方法中，質權人一般根據式(1)計算每只股票的VaR，進一步得到每只股票的質押率。它的問題在于各股票的VaR并不等價于其風險貢獻，這是因為質權人持有的是質押股票的組合，由于組合分散化效應，組合內各股票的加權VaR之和一般不等價于組合VaR，即各股票的加權風險之和并不等價于質權人的組合風險。事實上，根據成分VaR的定義(若某只股票被剔除出組合后，組合VaR的近似變化量即使成分VaR)可知，成分VaR反映了組合內各股票對組合的風險貢獻大小，各股票的成分VaR之和等于組合VaR。對應地，此時質押股票i的質押率βi為

本文利用R-vine Copula-GARCH模型刻畫多股票的聯合分布，在此基礎上計算組合VaR，并基于VaR分解技術得到各質押股票的成分VaR，進一步基于式(2)得到各股票的質押率。具體實現步驟如下：①基于AR(1)-GARCH(1, 1)估計各質押標的收益率的邊緣分布；②通過R-vine Copula函數估計多個質押標的間的多元相依結構；③利用Monte Carlo模擬法，計算基于R-vine Copula-GARCH的組合VaR；④根據組合VaR分解技術，得到各質押標的成分VaR，并據此得到其相應的質押率。

一、質押股票收益率分布模型

實證研究表明，股票收益率序列具有自相關性和異方差性。因此，本文利用AR-GARCH模型分析各股票收益率的邊緣分布，以刻畫其尖峰厚尾、波動聚集等典型分布特性。Bollerslev(1986)[3]研究表明AR(1)-GARCH(1,1)即可描述股票收益率的波動情況，模型如下：對t時刻的對數收益率序列進行一階自回歸AR(1)擬合，再對擬合后的殘差序列進行GARCH(1, 1)建模。考慮n只股票的組合，記股票i在t時刻的對數收益率為Ri,t，其中i=1, 2, …,n。基于AR(1)-GARCH(1, 1)的收益率建模方法如下

其中，Ri,t為對數收益率，μi為收益率均值，σi,t為收益率波動率，Zi,t為新息項，滿足E(Zi,t)=0、VAR(Zi,t)=1。μi，αi，ai,0，ai，bi為模型待估參數。

二、通過Copula函數估計n只股票間的多元相關結構

在實際中，股票間往往存在復雜相關結構(如尾部相關、非線性相關等)，基于線性相關關系的傳統VaR分析容易導致錯誤結果。而Copula函數不僅可用于度量股票之間的非線性相關關系，而且可將其邊緣分布與它們之間的相依結構分開研究，邊緣分布選擇也不受限制，它已成為構建多維隨機變量聯合分布和分析隨機變量間相依結構的重要工具。因此，本文選擇Copula函數描述多只股票間的相依結構。Copula函數定義如下：F為n維隨機變量X1,X2, …,Xn的聯合分布函數，其中Xi～Fi(i=1, 2,…,n)，即Fi為Xi的邊際分布函數，則F為邊際分布F1,F2,…,Fn的Copula函數C(.)，即

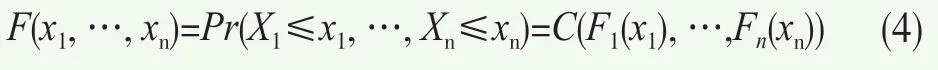
根據式(4)，多維聯合密度函數可以劃分成兩部分：邊緣密度函數和變量間的相依結構—Copula密度函數。不同的Copula描述了不同的相關模式，如Gumbel Copula函數對分布的上尾相關更加敏感(下尾相關系數為0)；Clayton Copula函數對分布的下尾相關更加敏感(上尾相關系數為0)；而t-Copula函數、Gaussian Copula函數、Frank Copula函數可用于描述對稱相關模式，其中Gaussian Copula函數和Frank Copula函數的上下尾相關系數均為0。然而，傳統Copula在描述多元相依結構時，只能選擇一種類型(例如，多元Clayton Copula則意味著資產之間均下尾相關)，它不能充分反映資產組合內兩兩資產間的相關性，從而導致對多維相依結構的估計存在偏差。而基于R-vine Copula理論構建的多維Copula模型，允許不同隨機變量之間存在不同的相依結構，即不同隨機變量之間可以存在不同形式的Copula相依結構，所以它在刻畫多維隨機變量間的相依結構上具有明顯優勢。吳海龍等(2013)[18]，馬鋒等(2015)[16]的實證研究均表明R-Vine Copula對投資組合VaR的預測效果最好。因此，本文采用R-vine Copula描述質押股票間的相依結構，R-vine Copula的密度函數如下

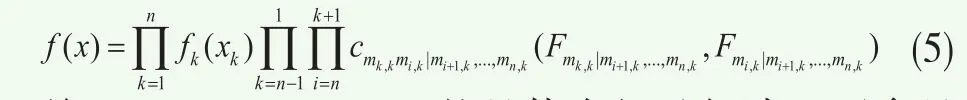
關于R-vine Copula的具體介紹及解讀，可參見Dissmann et al.(2013)[5]、Brechmann and Schepsmeier(2013)[4]。

三、基于R-vine Copula模型的組合VaR分析

基于步驟(一)和步驟(二)，R-vine Copula-GARCH構建了n只股票間的聯合概率分布函數。在得到任意n只股票的聯合分布和相依結構的基礎上，結合Monte Carlo模擬法，即可得到質權人資產組合的在險值VaR。

投資組合的VaR指的是：給定某個置信水平α∈(0,1)，VaR是使該組合損失L超過l(L≥l)的概率不大于1-α的最小l，即

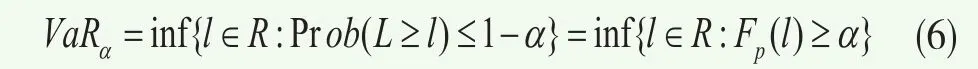
其中，Fp表示該投資組合收益率的概率分布函數。考慮包含n只股票的組合P，記第i個標的資產所占的權重為wi，那么質權人資產組合P收益率Rp,t為

基于R-vine Copula-GARCH模型的VaR并不存在解析解，此時，需采用Monte Carlo模擬法計算組合VaR。對步驟(二)確定的R-vine Copula進行抽樣，以模擬資產組合的收益率。需要注意的是，本文是對經過AR(1)-GARCH(1,1)模型濾波之后的標準化殘差收益序列{Zi,t}進行建模，因而R-vine Copula抽樣得到的是Zi,t的仿真序列。在模擬過程中，將t-1日的波動率σi,t-1代入GARCH模型中即可得到t日的波動率估計值，再將模擬得到的Zi,t和帶入AR模型中，便能計算出該股票t日收益率Ri,t的估計值則基于式(7)即可得到組合t日收益率的估計值，重復抽樣N次，即可計算出該質押標的組合當天的VaR值。另外，實踐中，通常根據金融資產1天的VaR1來估計金融資產T天的VaRT，方法如下：

四、組合VaR分解及質押率確定

一般來說，單純的組合VaR值對質權人了解風險的主要來源不能提供有意義的參考價值，質權人也無法據此得到質押率定價。因此，只有對組合VaR進行分解，使之能夠描述各股票對組合總體風險的貢獻大小，進而才能在此基礎上得到質押率。

設ri*表示組合在置信水平為α的條件下取最小值W*時資產i的收益率，此時

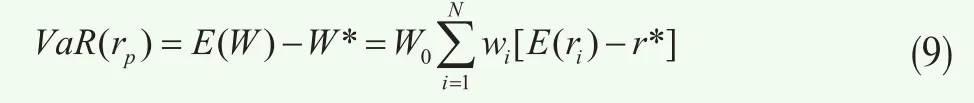
即組合VaR是資產權重{wi}，i∈p的齊次線性函數，由歐拉分配定理可知

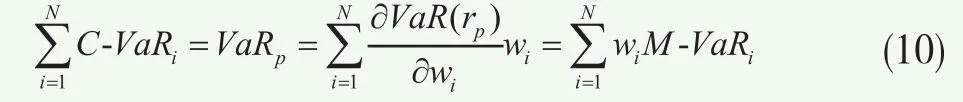
其中，M-VaRi為資產i的邊際VaR，此時可得到，

因此，只要知道組合中各股票的邊際VaR，即可根據式(11)可得到其成分VaR。估計邊際VaR的方法已經相對成熟，參見胡海鵬等(2003)[12]、吳緒權等(2006)[19]。本文不贅述。在估計得到邊際VaR之后即可得到各股票的質押率，即

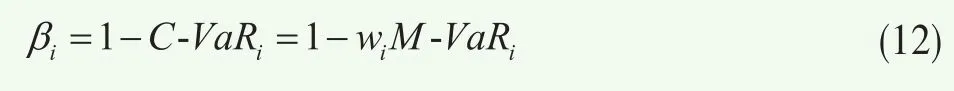
數值算例

一、數據描述

假設質權人持有6只質押標的，它們分別是“浦發銀行(600000)”、“恒瑞醫藥(600276)”、“深圳能源(000027)”、“東方雨虹(002271)”、“長海股份(300196)”和“朗科科技(300042)”，編號依次為1至6。事實上，在實際的股票質押業務中，雖然不同的質權人持有的股票組合是不同的，但是對任一質權人而言，質權人持有的質押股票組合是確定的，此時，即可進一步確定組合中各股票的波動率、各股票在組合中所占的權重以及質押股票之間的相依結構。一旦質權人根據實際質押股票組合確定了上述關鍵參數，即可使用本文提出的模型，根據質押股票的風險貢獻確定質押率的合理定價，本文模型具有通用性。

質權人基于組合質押視角，對這六只股票的收益率進行R-vine Copula-GARCH建模，并在得到每只股票風險貢獻的基礎上進一步確定其質押率。本文選取的樣本區間為2016年1月4日～2016年12月31日，質權人在2017年1月4日進行質押率定價。假設質權人持有的這6只股票的質押數量均為1億股，根據2016年12月31日的收盤價數據，這6只質押標的在質權人所持組合中的權重分為10%、29%、4%、14%、24%和20%(注：在實際質押業務中，質權人可根據其所持的實際質押股票數量得到質押標的的權重)。上述6只股票收益率(收益率指的是日對數收益率)序列的統計特征見表1。

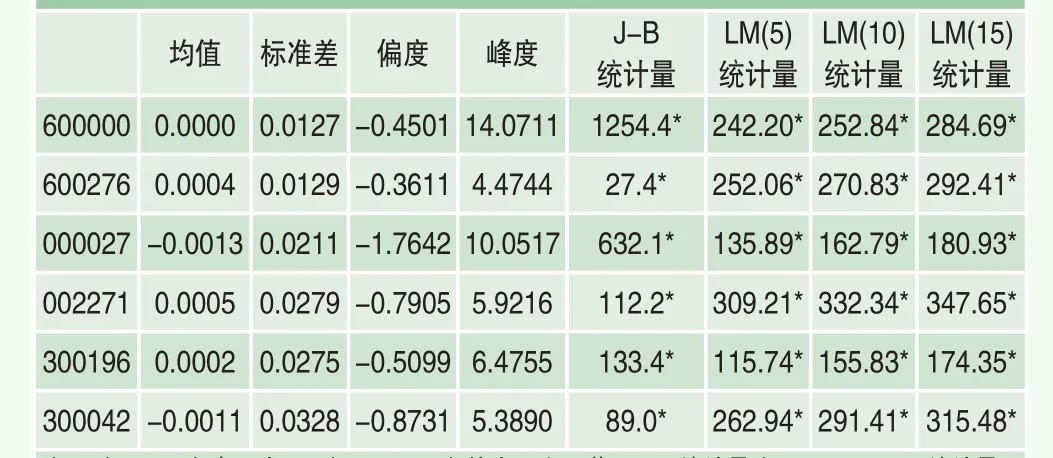
表1 樣本區間內質押標的收益率的統計特征

根據表1可知，6只質押標的收益率的偏度系數均小于0，說明質押標的收益率序列存在一定的左偏；6只質押標的收益率的峰度系數均大于3，說明質押標的收益率均呈現尖峰厚尾特征；另外，根據J-B統計量檢驗可知，收益率序列服從正態分布的假設被拒絕；而Engle’s ARCH Test統計量表明，在1%顯著性水平上，收益率序列具有明顯的ARCH效應。為消除單只質押股票收益率序列的自相關性和異方差性，本文采用AR-GARCH模型對質押股票收益率進行建模，以刻畫其尖峰厚尾、波動聚集的特征。

二、股票收益率的邊際分布估計

利用AR(1)-GARCH(1, 1)模型對這6只股票的收益率序列進行擬合，參數估計結果見表2。

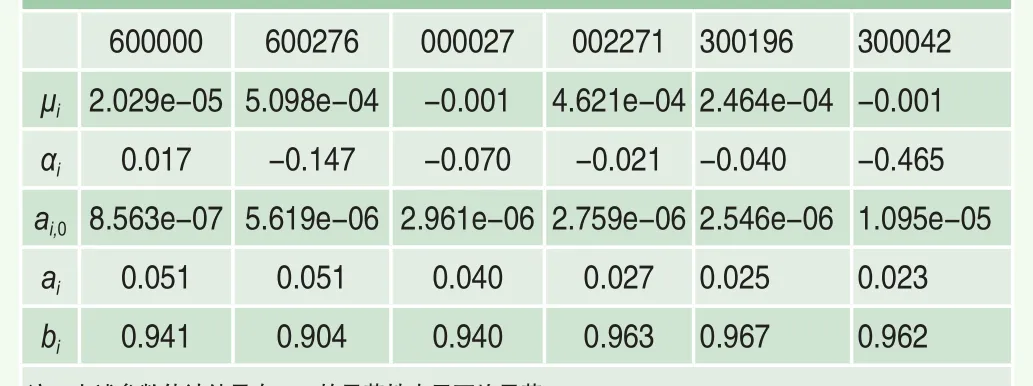
表2 AR(1)-GARCH(1,1)模型的參數估計結果

三、基于R-vine Copula的聯合分布估計

本節估計這6只股票的R-vine Copula結構，R-vine Copula模型的輸入變量是“經過AR-GARCH模型濾波之后的標準化殘差收益序列{Zi,t}”，利用Python的pyvine0.4.2模塊直接得到R-vine Copula模型的參數估計結果，見表3。

表3中，節點i表示股票i的概率密度分布，例如節點1表示股票1(即浦發銀行)的概率密度分布，節點23表示股票2和股票3(即恒瑞醫藥和深圳能源)的聯合概率密度，節點46|5表示的則是條件概率密度。根據表3可知，質押股票之間存在復雜的相依結構(例如，節點1和節點2之間的相依結構是Student Copula，而節點5和節點6之間的相依結構是Clayton Copula)，單純利用多元Copula很難刻畫資產之間的相依結構，因為多元Copula假定所有資產之間僅存在一種Copula相依結構。這意味著R-vine Copula模型在對多維資產收益率數據進行建模時更加具有靈活性，在對兩兩資產之間的Copula的選擇上更為準確。

四、組合VaR分解及其相應的質押率

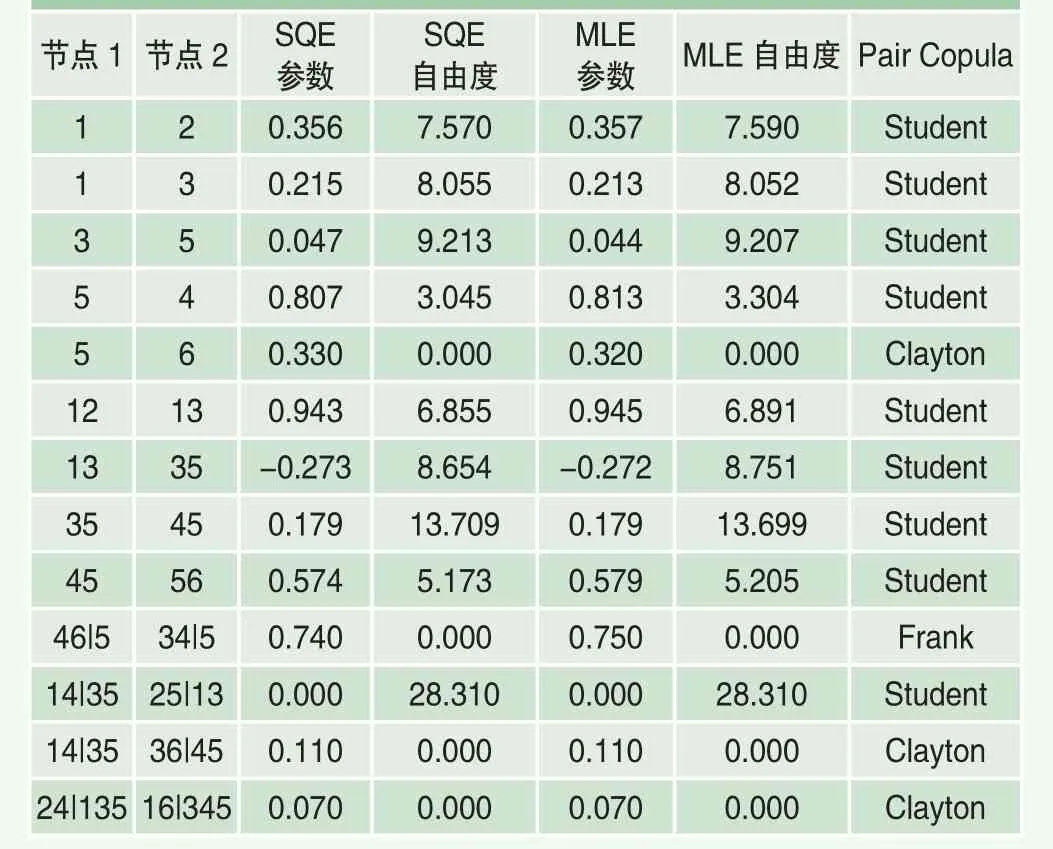
表3 R-vine Copula模型的參數估計結果

在得到R-vine Copula模型之后，利用Python模塊pyvine得到基于R-vine Copula抽樣的仿真序列。值得注意的是，R-vine Copula抽樣得到的是Zi,t的仿真序列，即R-vine Copula抽樣得到的是Zi,t的仿真序列，即R-vine Copula抽樣得到的是經AR-GARCH模型濾波之后的標準化殘差收益序列{Zi,t}。股票i在t日收益率Ri,t的估計值的計算方法如下：

將t-1日的波動率σi,t-1代入GARCH模型中計算質押標的在t日的波動率的估計量σi,t-1，再將模擬得到的Zi,t和帶入AR模型中，便能得到該股票t日收益率Ri,t的估計值結合其權重向量，利用式(7)即可得到質權人所持組合在t的收益率的估計值重復上述步驟N次，便可得到基于R-vine Copula-GARCH模型的組合VaR值。在此基礎上，利用組合VaR分解技術，并結合式(13)即可得到各股票的質押率，見表4。為便于闡述模型效果，本文還列示了獨立VaR情形和傳統組合VaR分解情形下的質押率定價結果。

通過對比表4可得如下結論：

第一、質權人是否基于組合視角將對股票質押率定價產生重要影響。單純對比獨立VaR情形和傳統組合VaR分解情形，二者的區別在于是否考慮組合的分散化效應，組合的風險并不是單一股票風險的簡單相加，即質權人的整體質押業務風險不應是各股票所含風險的加權平均。傳統組合VaR分解考慮了組合分散化效應，它對應的質押率要高于不考慮分散化效應的獨立VaR情形，即質權人不基于組合視角將低估質押率。

第二、基于R-vine Copula-GARCH VaR分解情形的質押率低于傳統組合VaR分解情形，即忽視收益率尖峰厚尾特征和收益率之間的復雜相關結構，將高估質押率。傳統組合VaR模型假定股票收益率之間服從多元正態分布，即質押標的收益率之間均是線性相關，且不存在尖峰厚尾特征。但正如前文實證結果所示，股票收益率均存在尖峰厚尾、波動聚集現象(見表3)，而且股票之間存在復雜相依結構(見表4)，在考慮這些因素之后，質押率應有所降低。

對比這三種定價情形，質權人不基于組合視角定價將低估質押率；進一步來比較前兩種定價方法，同是基于組合視角，當充分質押標的收益率尖峰厚尾和復雜相關時，質押率變會稍低。這就意味著本文結合R-vine Copula模型和AR(1)-GARCH(1, 1)模型給出的質押率定價方法，既有利于提高質權人風險防范度，又可避免質權人過度防范風險，在三種方法中，最能實現風險-收益的平衡。

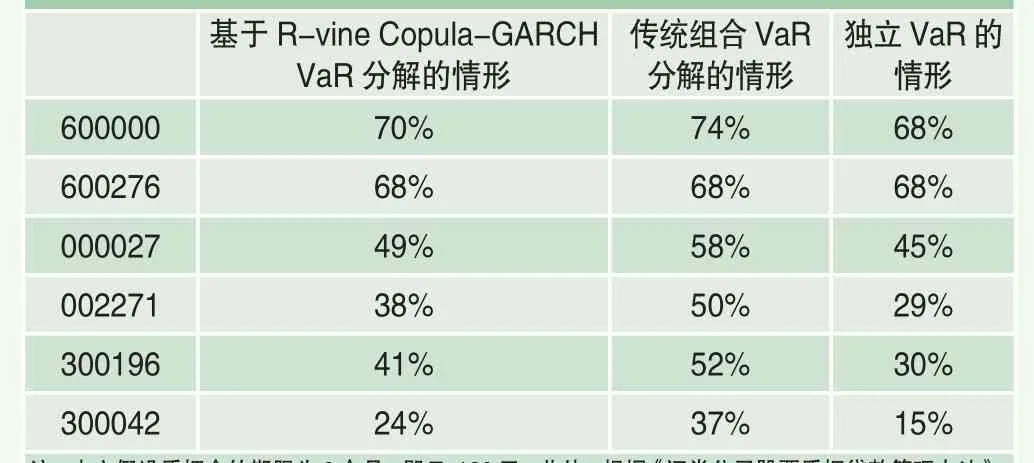
表4 不同模型下的質押率定價對比

本文不僅具有理論意義，而且也具有現實指導意義。目前，實踐中的股票質押率定價方法嚴重落后于理論，證券公司一般根據所謂的“五四三”標準來設定不同個股的質押率，即令波動率最小的主板股票質押率為50%，中小板為40%，而波動率最大的創業板股票質押率為30%。但是這類定價方法精確度明顯不夠，進而導致質權人風險--收益難以平衡。而本文提出的考慮組合分散化效應的質押率定價方法，為國內證券公司在質押率定價、風險控制等微觀層面的設計提供了明確的指引。

結論

為促進股票質押業務健康發展，合理匹配質權人的收益與風險，優化質押率定價顯得頗為重要。而理論界對質押率做定價基本都針對單一股票標的，這事實上忽略了質權人的組合分散化效應對質押率定價的影響。此外，實踐中廣泛使用的VaR定價方法，也忽視了質押標的收益率尖峰厚尾、波動聚集等特征對質押率定價的影響。鑒于此，本文將研究視角由單一股票質押率定價擴展至考慮分散化效應的組合質押問題，首先利用AR(1)-GARCH(1, 1)估計各質押標的收益率的邊緣分布函數，然后通過R-vine Copula 函數估計多個質押標的間的多元相關結構，最后結合Monte Carlo模擬和組合VaR分解技術得到質押率定價模型，并通過數值算例驗證上述定價方法的優勢。

概括而言，本文貢獻主要包括：第一，把單一股票質押問題擴展至考慮分散化效應的組合質押問題，更切實際；第二，充分考慮了質押標的收益率的尖峰厚尾特征及其復雜相關結構，結合AR-GARCH模型及R-vine Copula模型，根據質押標的的風險貢獻進行質押率定價，有助于提高實際質押業務的整體風險——收益平衡性。