關于熱力學空間概念的探討

張啟南

北京航空航天大學 航空科學與工程學院， 北京 100083

概念探討

關于熱力學空間概念的探討

張啟南*

北京航空航天大學 航空科學與工程學院， 北京 100083

在氣體力學研究中，不可避免地將引用熱力學的基本定律，過去在不少工科著者所用的論述中常將傳熱量Q和氣體所做的功W的微增量寫為dQ和dW。但從嚴格的數學理論而言，這是不正確的表達式。筆者在參與《航空空氣動力手冊》的編審中曾經提出過此問題，在手冊的再版時已經改正為δQ和δW。但此后一些氣體力學的著作未能引起注意，仍然習慣地寫成dQ和dW。為此，在本文中作一個嚴格的證明，并提出了熱力學空間的概念，以澄清以往的混淆。

熱力學空間； 幾何空間； 狀況參數； 積分型全微分條件； 微分型全微分條件

1 全微分存在的條件

數學中專門研究全微分的理論說明：

若P、Q、R為x、y、z3個自變量在單連通域中的連續函數，而且都存在連續的偏導數。和式Pdx+Qdy+Rdz是某函數F(x，y，z)的全微分的必要充分條件為

1) 積分型條件

∮Pdx+Qdy+Rdz=0

(1)

2) 微分型條件

(2)

注意此兩條件是等價的，即只有滿足此條件，全微分式dF=Pdx+Qdy+Rdz才成立。

2 熱力學第一定律

氣體的物理性質由p、v、T3個狀況參數唯一確定。其中：p為壓強，v為比容，T為絕對溫度。氣體微分體的能量守恒定律為

δQ=dE(T)+pdv

(3)

此即熱力學第一定律。式中：E為氣體的內能，是T的單自變量函數。因此

dE(T)=cdT

(4)

式中：c為氣體的定容比熱。

氣體所作的功就是pdv，可表示為δW。注意Q和W前面的符號暫時寫為δ。

將式(3)寫為

δQ=cdT+0dp+pdv

(5)

與和式Pdx+Qdy+Rdz對比可見

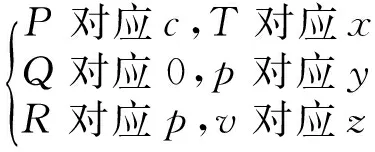
代入微分型的全微分條件：

可見

(6)

顯然不滿足全微分的條件。因此δQ不是全微分，不能寫成dQ。

類似地將氣體作的功表達為

δW=pdv=0+0dp+pdv

(7)

也可以證明δW不是全微分，不能寫成dW。很明顯Q和W不是代表氣體狀況的變量，而是氣體運動和變化過程中出現的物理量。

3 焓和熵的概念

對于完全氣體(Perfect Gas)，它服從克拉貝隆方程

pv=kT

(8)

式中：k為氣體常數，選用的是氣體動力學中最常用的形式。

將熱力學第一定律δQ=cdT+pdv兩邊均除以T，可得

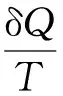
cd(lnT)+kd(lnv)

(9)

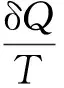
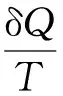
(10)

式中：S為熵。

再看

δQ+vdp=cdT+pdv+vdp=cdT+d(pv)

(11)

顯然，這是全微分，可定義為

dH=cdT+d(pv)

(12)

式中：H為焓。熵S及焓H表達的是氣體的物理性質，和p、v、T一樣，是氣體的狀況參數。

焓的物理意義是氣體的內能與壓力勢能之和，熵的物理意義在熱力學第二定律中說明。

4 熱力學第二定律

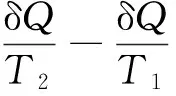
因為微體1失去的熱量δQ就是微體2得到的同樣熱量，得到的熱量為正，失去的熱量則為負,因此dS>0。若考慮全閉合系統則∑dS>0。因此有限空間的閉合系統中，熱傳輸過程的熵總是增加的。

狀況參數的增量由全微分d表達;非狀況參數的增量則用δ表達，以示區別。這種數學表達方式與物理意義的對應是數學物理結合的完美范例。

5 結 論

以上從全微分存在的微分條件出發，證明了dH、dS為全微分；δQ、δW為非全微分。可見當氣體的微體經過某物理變化的閉合循環時，

(13)

即焓與熵回到原值，與積分過程無關,與物理變化過程無關。而

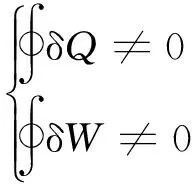
(14)

即氣體微體經過閉合循環過程，將會吸熱和放熱，將會對外做功或外面對它做功。熱和功之增減量依賴于物理變化過程。

至此可以提出一個更為綜合的概念：將氣體的熱力學狀況參數p、v、T定義為“熱力學空間”。實際上數學理論中的空間概念已經超越了幾何空間的概念，有的作者常常不自覺地將“空間”之概念約束在幾何范圍中。其實自變量x、y、z不一定是幾何量，可以是任何的物理量，例如在相對論中所用的自變量是x、y、z、t(四維)即“時空空間”的概念。相應的在氣體力學中p、v、T作為自變量來描述熱力學的物理量及定律，這就是“熱力學空間”的概念。

總之幾何空間的概念是3個自變量x、y、z唯一地描述了一點在三維空間的幾何位置。熱力學空間的概念是3個自變量p、v、T唯一地描述了氣體微分體的熱力學性質(狀況參數)。這樣的綜合與推廣非常自然，完全符合辯證唯物論的認識規律。

6 后 記

筆者于1990年在北京航空航天大學出版社出版了《工程物理中的張量場論》一書，討論的“場”即是物理量在幾何空間中的分布和變化，這和本文中的“空間”概念是完全相通的。因此若能將兩者融合起來，更能反應大自然的客觀規律。現在已經到了各基本學科綜合起來發展的時代，這是值得一提的。

(責任編輯： 蔡斐)

URL：www.cnki.net/kcms/detail/11.1929.V.20170512.1549.010.html

*Correspondingauthor.E-mail:qal@buaa.edu.cn

Ontheconceptofthermodynamicspace

ZHANGQi’nan*

SchoolofAeronauticalScienceandEngineering,BeihangUniversity,Beijing100083,China

Inthestudyofpneumatics,itisinevitabletorefertothebasiclawsofthermodynamics.Inthepast,anumberofengineeringauthorsoftenwroteheatQandthemicro-incrementsoftheworkdonebythegasWasdQanddW,whichare,however,notcorrectexpressionsasfarasastrictmathematicaltheoryisconcerned.WhenparticipatingintheeditingoftheAviationAirForceManual,theauthorraisedthisissue.Inthesecondeditionofthemanual,dQanddWwerecorrectedtoδWandδQ.Butsomepneumaticworksstillfailtopayattentiontotheproblem,andarestillusedtousingdQanddW.Inthisarticle,arigorousproofisconductedandtheconceptofthethermodynamicspaceisproposedtoclarifytheconfusioninthepast.

thermodynamicspace;geometricspace;statusparameter;integral-totaldifferentialcondition;differential-totaldifferentialcondition

2016-10-18；Revised2017-04-26；Accepted2017-05-05；Publishedonline2017-05-121549

2016-10-18；退修日期2017-04-26；錄用日期2017-05-05； < class="emphasis_bold">網絡出版時間

時間：2017-05-121549

www.cnki.net/kcms/detail/11.1929.V.20170512.1549.010.html

.E-mailqal@buaa.edu.cn

張啟南. 關于熱力學空間概念的探討J. 航空學報，2017，38(8)：721356.ZHANGQN.OntheconceptofthermodynamicspaceJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):721356.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.721356

V211

A

1000-6893(2017)08-721356-03