基于分層優化的異步電動機多目標優化設計

莊石榴, 王愛元, 宋林峰， 陳 哲， 王明星

(上海電機學院 電氣學院， 上海 201306)

基于分層優化的異步電動機多目標優化設計

莊石榴, 王愛元, 宋林峰， 陳 哲， 王明星

(上海電機學院 電氣學院， 上海 201306)

引入分層優化的方法對電動機進行多目標優化設計。先從局部進行優化設計，將傳統異步電動機中的單層繞組改造成單、雙層繞組，并分析其對氣隙磁場的影響；然后，選取電動機的定子內、外徑之比、每槽導體數、定子和轉子槽寬為變量，結合正交試驗法和Ansys Maxwell有限元軟件對三相異步電動機整體進行多目標優化設計。仿真結果表明，與優化前相比，優化后電動機的效率和功率因數都得到了一定提升。

三相異步電動機； 分層優化； 繞組形式； 正交試驗法； 多目標優化

異步電動機作為主要的用電設備，其用電總量占世界工業用電量的60%[1]，因此,若其效率和功率因數能夠進一步提升，將會產生很大的經濟和社會效益。

效率和功率因數是異步電動機的兩項重要性能指標，它們之間有一定的聯系，也有很大區別。從運行角度來講，電動機的效率隨負載的增大先增大、后下降，存在一個最高效率；考慮負載的變化，設計最高效率約為負載的75%。異步電動機屬于感性負載，通常從空載開始，功率因數隨負載的增大先快速增大，到一定程度后再緩慢增加，但功率因數始終是滯后的。

對異步電動機的優化設計通常是從提高效率開始的，文獻[2-4]中將電動機的定子繞組設計成單、雙層繞組，以達到節省銅用量和提升效率的目的。文獻[5-6]中通過對電動機槽型尺寸的研究，得出槽口寬度、槽寬和槽底半徑對損耗影響較大。文獻[7]中通過優化電動機的每槽導體數、鐵芯長度等參數來提升其效率。文獻[8-10]中分別利用免疫克隆算法、蟻群算法、粒子群算法對電動機結構進行優化設計，由于算法都是全局優化方法，故建立目標函數時非常復雜。文獻[11-13]中引入田口法來優化永磁同步電動機，通過改變電動機的結構參數尺寸來優化其性能，該方法避免了電動機結構的復雜化，簡化了計算，比較簡便有效。

本文對異步電動機的效率和功率因數兩項指標進行優化，采用分層優化的方法，先對繞組進行結構形式優化，使得電動機性能獲得一定提升；然后，對電動機進行多目標、多變量的整體優化設計。以11 kW的4極三相異步電動機為例，采用正交試驗和Ansys Maxwell軟件相結合的方法對其進行優化設計，最后采用方差分析法選取優化變量。結果表明，優化后電動機的效率和功率因數都得到了提升。

1 繞組形式的改造

11 kW的4極三相異步電動機的主要參數如表1所示。

表1 電動機的主要參數

電動機原來采用單層交叉繞組，該繞組的線圈兩邊可以同時嵌入到槽內，嵌線容易，便于實現機械化。而雙層疊繞組通常用于功率較大的感應電動機，選擇短節距，如5/6可以消除5、7次諧波，可改善電動機的性能[14]。

當電動機采用雙層短距繞組時，某些槽內的上、下層導體同屬一相，且電流方向相同；而某些槽內的上、下層導體不同相。若將屬于同相的上、下層導體結合起來用單層繞組代替，而槽內不同相的上、下層導體仍保持原有的雙層繞組，按照同心式繞組端部形狀布線連接，就形成了既有單層繞組又有雙層繞組的單、雙層繞組連接方式，其繞組連接方式如圖1所示。

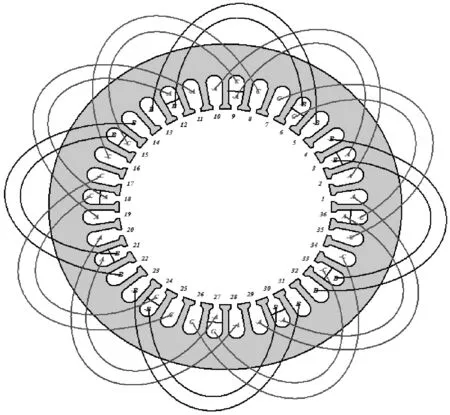
圖1 單、雙層繞組接線圖

對本文選取的三相異步電動機，先在Ansys Maxwell有限元軟件中構建電動機模型；然后，改變繞組形式分別對其進行仿真，得到該異步電動機在單層繞組和單、雙層繞組下的徑向氣隙磁密波形圖，再對其進行傅里葉分解得到如圖2所示的傅里葉分解圖。由圖可見，將電動機的單層繞組改為單、雙層繞組后，徑向氣隙磁密的基波幅值由0.76 T提升到0.80 T，氣隙磁密波形得到改善。

使用Ansys Maxwell分別對單層繞組和單、雙層繞組形式下的電動機進行仿真實驗，得出電動機的各種損耗及功率因數cosφ，并計算得到它們的效率η，表2給出了不同繞組下電動機的性能參數。由表可見，將單層繞組改成單、雙層繞組后，電動機的效率η和功率因數cosφ都得到了一定提高。

綜上所述，與單層繞組相比較，單、雙層繞組具有雙層繞組的優點，即具有較好的氣隙磁場波形，且具有較好的起動性能和較低的附加損耗。

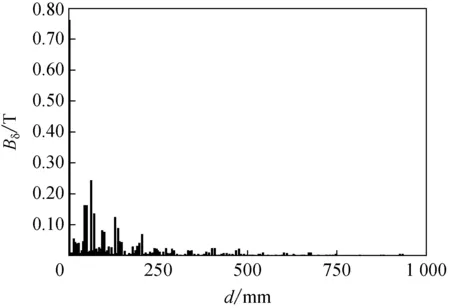
(a) 單層繞組

(b) 單、雙層繞組

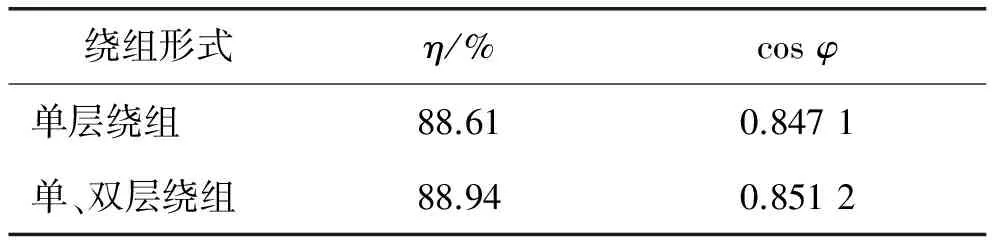
表2 不同繞組下的電動機性能參數

2 基于正交試驗法的優化設計

2.1正交試驗設計

正交試驗法是由日本統計學家田口玄一首先提出的[15]，是一種應用于工程的局部優化算法。與一些全局優化的算法相比，它可以使用最少的試驗數據、試驗次數來得到最優的設計參數組合，更加直觀、簡捷，可節省大量的時間和成本，提高效率。本文基于正交試驗的異步電動機多目標優化設計的步驟如下：

(1) 根據優化的目標，合理選擇所需的優化參數；

(2) 依據實際情況，對所選取的每個優化參數給定一個合理的取值范圍，根據前期的仿真結果以及優化參數經驗值，進行電動機優化參數及影響因子取值，如表3所示；

(3) 建立正交試驗表；

(4) 利用有限元軟件求解正交試驗矩陣；

(5) 對比分析實驗數據，找到參數最優值 ，然后與優化前相比較。

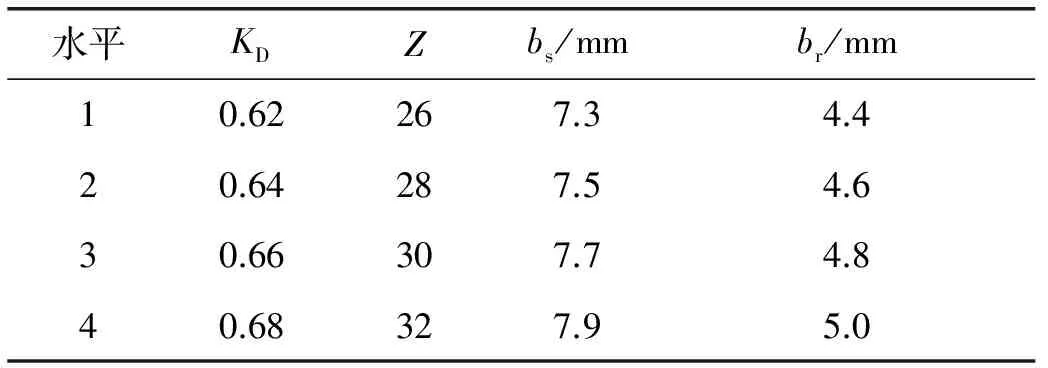
表3 電動機優化參數及影響因子取值

注：KD為定子內、外徑比；bs為定子槽寬；br為轉子槽寬

本文所選取的電動機優化參數有4個，水平數也為4，故正交矩陣為L16(44)。若按照傳統的電動機優化方法需進行256次有限元計算，而采取正交試驗只需進行16次有限元計算，大大縮短了時間，提升了效率。

確定正交試驗矩陣后，在Ansys Maxwell中對不同參數分別構建異步電動機仿真模型，利用瞬態場求解器對每組實驗進行有限元分析計算。表4所示為正交試驗表及有限元分析結果。

2.2試驗結果分析

本文采用數據統計的方法，先進行平均值分析，包括實驗結果平均值分析和每個參數各水平下對應的η或cosφ計算結果的平均值分析；然后方差分析，最終得出最優的結果。

表4所示為正交試驗表及有限元分析結果。先分別對表中16次實驗結果的η和cosφ計算平均值，得到η的平均值為89.215%，cosφ的平均值為0.853 6。然后，分別計算得到優化參數在各水平下η和cosφ的平均值，如表5所示。

最后，利用方差分析的數學方法計算各參數的變化對η或cosφ的影響為

(3)

表4 正交試驗表及有限元分析結果

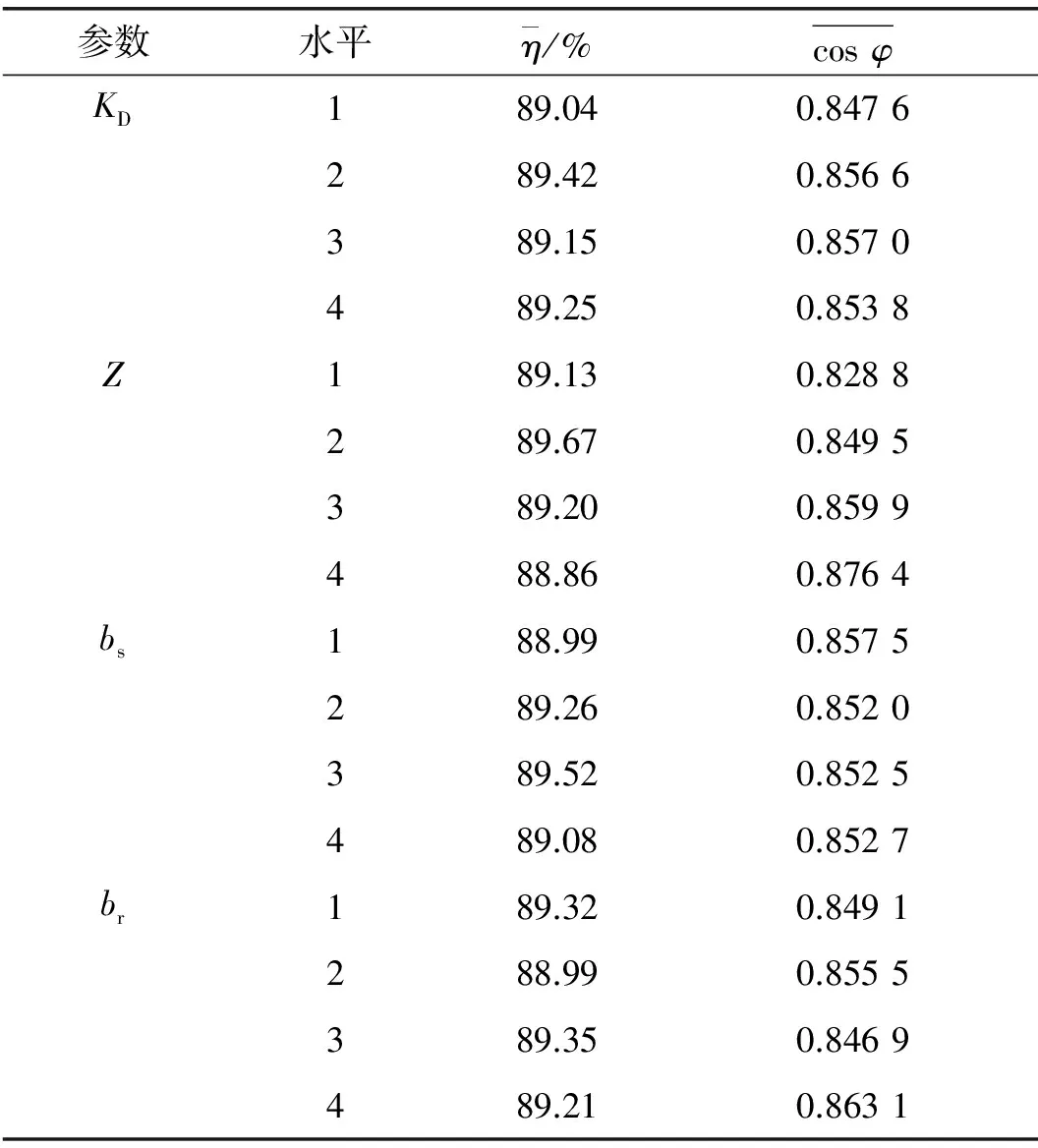
表5 各性能指標平均值

計算得到選取的KD、Z、bs、br4個優化參數變化對η和cosφ的影響，以及其在所有參數中所占比例如表6所示。

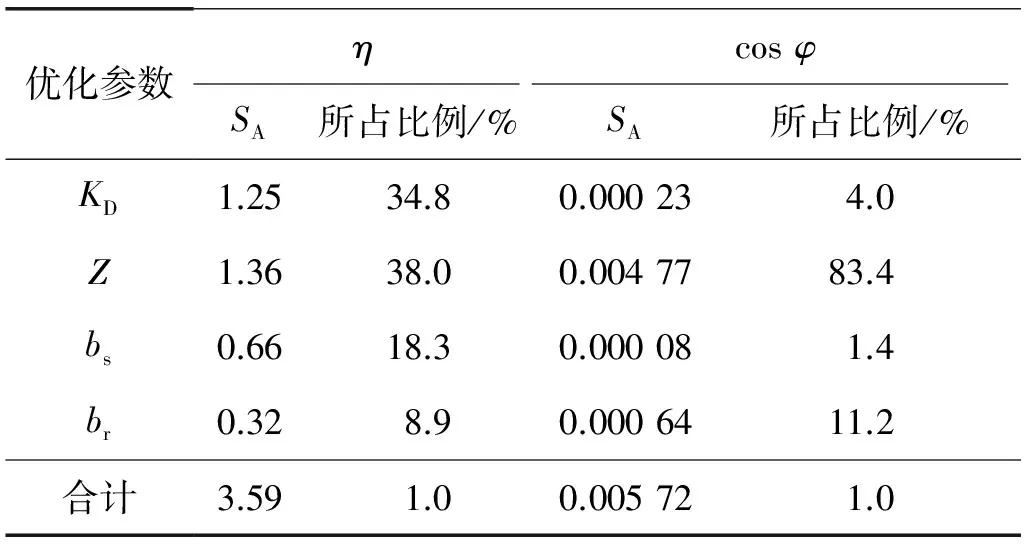
表6 優化變量對電動機性能影響所占的比重

由表可見，Z在所有參數中對cosφ的影響最大，占83.4%，而對η的影響占38.0%，因此，對于Z，主要考慮其對cosφ的影響；KD和bs對η的影響較大；而相比較而言，br對cosφ的影響較大，對η的影響較小；因此，參考表5，選取KD在水平2、Z在水平4、bs在水平3、br在水平4的數值，即KD=0.64，Z=32，bs=7.7 mm,br=5.0 mm為最終優化結果。

根據得到的優化參數在Ansys Maxwell中建立有限元模型，仿真得到優化后的η=89.562%，cosφ=0.856 4。與表2的數據相比較可見，經過分層優化后的電動機與優化前相比較性能有一定的提升。

3 結 語

本文采用分層優化的方法對電動機進行多目標多變量的優化設計，先將三相異步電動機原有的單層繞組改為單、雙層繞組，再進行整體多變量、多目標的優化設計。采用正交試驗選取KD、Z、bs、br作為優化參數，以電動機的η和cosφ作為優化的目標，在有限元軟件中建模仿真，最終確定最優的參數組合，將優化后的結果和優化前相比較，η和cosφ都得到一定提高，這對實際的應用具有一定參考價值。

[1] 黃國治，傅豐禮. 中小旋轉電機設計手冊 [M].2版.北京：中國電力出版社，2014：1.

[2] 易曉榮，馬德鑫. 單雙層繞組應用于Y2-200L-2提高電機效率 [J]. 電動機技術，2008(5)：13-14.

[3] 張亮，李瑞東. 電動機單雙層繞組的設計 [J].防爆電機，2016,51(5)：15-17.

[4] 馬德鑫. 單雙層繞組的組成及其計算方法 [J]. 中小型電機技術情報,1979,6(4):7-11.

[5] KIM J W, KIM B T, KWON B I. Optimal stator slot design of inverter-fed induction motor in consideration of harmonic losses [J].IEEE Transactions on Magnetics,2005,41(5):2012-2015.

[6] 趙海森,劉曉芳,楊亞秋，等. 基于時步有限元分析的超高效電機定子槽形優化設計 [J]. 中國電機工程學報,2011,31(33):115-122.

[7] AGAMLOHH E B, BOGLIETTI A,CAVAGNINO A. The incremental design efficiency improvement of commercially manufacture induction motors [J].IEEE Transactions on Industry Applications,2013,49(6):2496-2504.

[8] 鄭云卿. 基于多目標免疫克隆算法的三相異步電機優化設計 [D].合肥：安徽大學，2012.

[9] 陳慶峰. 基于多目標蟻群算法的三相異步電機優化設計 [D].杭州：浙江工業大學，2011.

[10] 孟大偉，張羽，趙成. 粒子群算法在電機優化設計中的應用 [J].防爆電機，2011，46(5):1-3.

[11] KIM S I, LEE J Y, KIM Y K, et al. Optimization for reduction of torque ripple in interior permanent magnet motor by using the Taguchi method [J].IEEE Transactions on Magnetics, 2005, 41(5):1796-1799.

[12] 王曉遠，張力，許衛剛. 基于田口算法的內置式永磁同步電機多目標優化設計 [J].微電動機，2016,49(5):1-5.

[13] 王艾萌，溫云. 田口法在內置式永磁同步電機優化設計中的應用 [J]. 華北電力大學學報(自然科學學報)，2016,43(3):39-44.

[14] 陳世坤. 電機設計 [M].2版.北京：機械工業出版社，2000:235.

[15] 曾鳳章，趙霞.田口方法及其標準化設計 [J].機械工業標準與質量，2003(11)：7-9.

Optimization Design of Multi-Object Hierarchical Optimization of Asynchronous Motor

ZHUANGShiliu,WANGAiyuan,SONGLinfeng,CHENZhe,WANGMingxing

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

A method of hierarchical optimization is used to optimize the motor. From the local optimization design, single layer winding of a traditional three-phase asynchronous motor is converted into single double-layer winding. Its effect on the air-gap magnetic field is analyzed. The ratio between the inner and outer diameters of the motor stator, the number of each slot conductor, and widths of the stator and therotor slot are selected as variables. Combining with an orthogonal test method and the Ansys Maxwell finite element software, optimization design of the three-phaseasynchronous motor is carried out. Simulation results show that efficiency and the power factor of the motor are improved as compared with the pre-optimized motor.

three-phase asynchronous motor; hierarchical optimization; winding form;orthogonal experimental method; multi-object optimization

2017 -07 -28

莊石榴(1993-)，男，碩士生，主要研究方向為電機設計與優化 ，E-mail:1224680899@qq.com

2095-0020(2017)05 -0281-05

TM 343.2

A