改進的GNSS信號快速捕獲檢測算法

張超逸，曾丹丹，李金海，孫金海，閻躍鵬

(中國科學院 微電子研究所，北京 100029)

改進的GNSS信號快速捕獲檢測算法

張超逸，曾丹丹，李金海，孫金海，閻躍鵬

(中國科學院 微電子研究所，北京 100029)

為了滿足衛星導航接收機在高動態應用場景中對衛星信號快速捕獲的需求，本文針對全球導航衛星系統(global navigation satellite system，GNSS)信號的捕獲檢測問題提出了一種改進的檢測算法。該算法結合了N中取M檢測算法和唐檢測算法的優點，考慮信號存在和不存在時的兩種情況，通過設置多級門限檢測機制，加快了信號存在時的檢測確認速度和信號不存在時的剔除速度。實際數據測試表明，改進算法在檢測概率沒有任何損失的情況下，捕獲檢測速度相對于N中取M算法提高3倍，相對于唐檢測算法提高1/3。

衛星導航接收機； 高動態； 快速捕獲； 全球導航衛星系統；N中取M檢測算法； 唐檢測算法； 多門限檢測； 捕獲檢測速度

全球衛星導航系統在各行各業中的應用日益廣泛。導航接收機設計中首次定位時長是一個重要指標，捕獲檢測算法的性能對這一指標至關重要[1]。在高動態應用場景中，GNSS信號強度較高，但載體運動時間非常短，因此對接收機的首次定位時間，特別是有星歷注入模式下的熱啟動時間要求非常高。而接收機準確快速地完成GNSS信號的捕獲及后續檢測是獲得快速啟動的關鍵因素。在實際接收機設計中，完成捕獲搜索后，需要對捕獲結果進行檢測確認。由于單次檢測結果的檢測概率低且虛警概率高[2]，無法滿足系統對衛星信號的捕獲要求，因此需要進行多次檢測以提高整體的信號檢測概率，降低虛警概率。常見的捕獲檢測算法有N中取M檢測算法和唐檢測算法[2]。本文首先對這兩種檢測算法進行了分析說明；接著提出了一種改進的檢測算法，結合N中取M檢測算法和唐檢測算法的優點，采用多門限判決機制，提高了檢測速度。該檢測算法在強信號條件下捕獲檢測速度快、性能好，適用于實時性要求較高，信號無遮擋且需要有較快捕獲檢測速度的高動態場景。

1 捕獲檢測算法分析

1.1N中取M檢測算法

N中取M檢測算法將信號與門限比較，大于門限則計數器J加1，小于門限J不變，每次比較計數器K減1。當K等于0時進行判決，若此時J不小于M則檢測成功，否則檢測失敗。這里J初始值取0，K初始值取N。其算法流程如圖1所示。

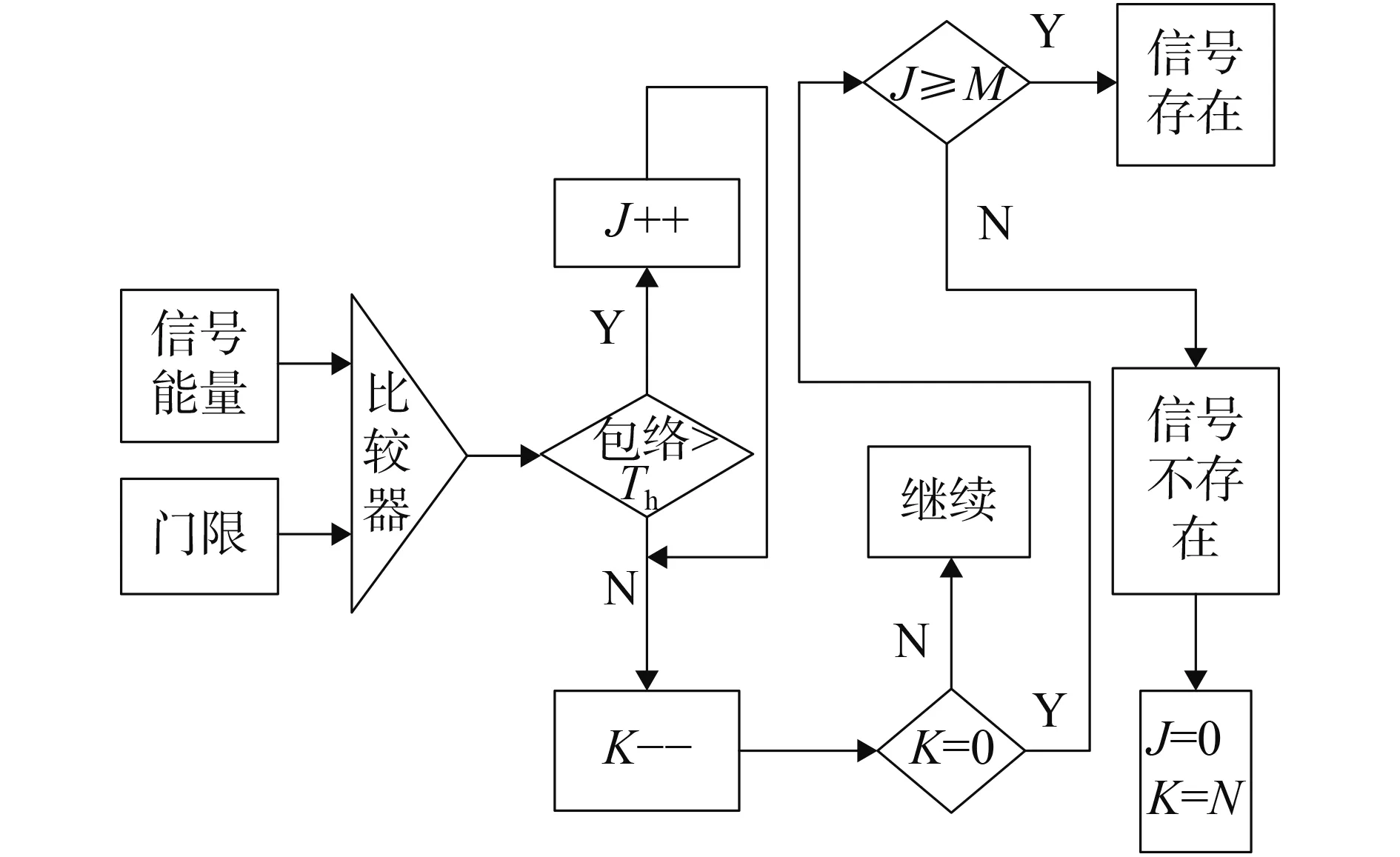
圖1 N中取M檢測算法流程Fig.1 M-of-N detection algorithm flow

圖中Th為單次比較的門限值。可以看出N中取M檢測算法是一種固定檢測次數的檢測器，其檢測過程滿足Bernoulli隨機過程，超過門限的信號數目n具有二項式分布。N次試驗的系統虛警概率[3]為

1-B(M-1,N,Pfa)

(1)

式中：Pfa為捕獲檢測的單次虛警概率，B是Bernoulli積分。N次試驗的系統檢測概率[3]為

1-B(M-1,N,Pd)

(2)

式中：Pd為單次檢測概率。不同信噪比、N中取M檢測算法的仿真結果如圖2,算法性能如表1所示。

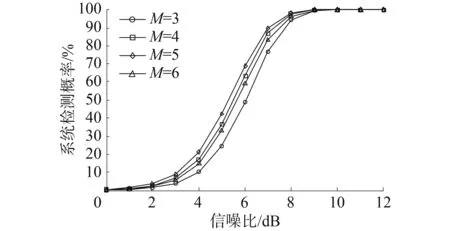
圖2 N中取M檢測算法仿真結果(N=8)Fig.2 Simulation results of M-of-N detection algorithm(N=8)

檢測次數M(N=8)單次虛警概率/%信噪比/dB駐留平均數N30.267.6841.107.2852.867865.847.28

從圖2和表1中可以看出M=5是最佳值,此時檢測概率最高。該算法在系統檢測概率達到90%，系統虛警概率等于10-6條件下，信號檢測門限信噪比為7～8 dB。N中取M檢測算法的缺點是不論信號強弱，檢測駐留次數均為N次，導致檢測速度非常慢。

1.2唐檢測算法

唐檢測算法將信號與門限比較，大于門限檢測計數器K加1，小于門限檢測計數器K減1；當K大于等于檢測次數門限A時，認為信號存在；當K=0時認為信號不存在。這里K的初始值取B。其算法流程如圖3所示。

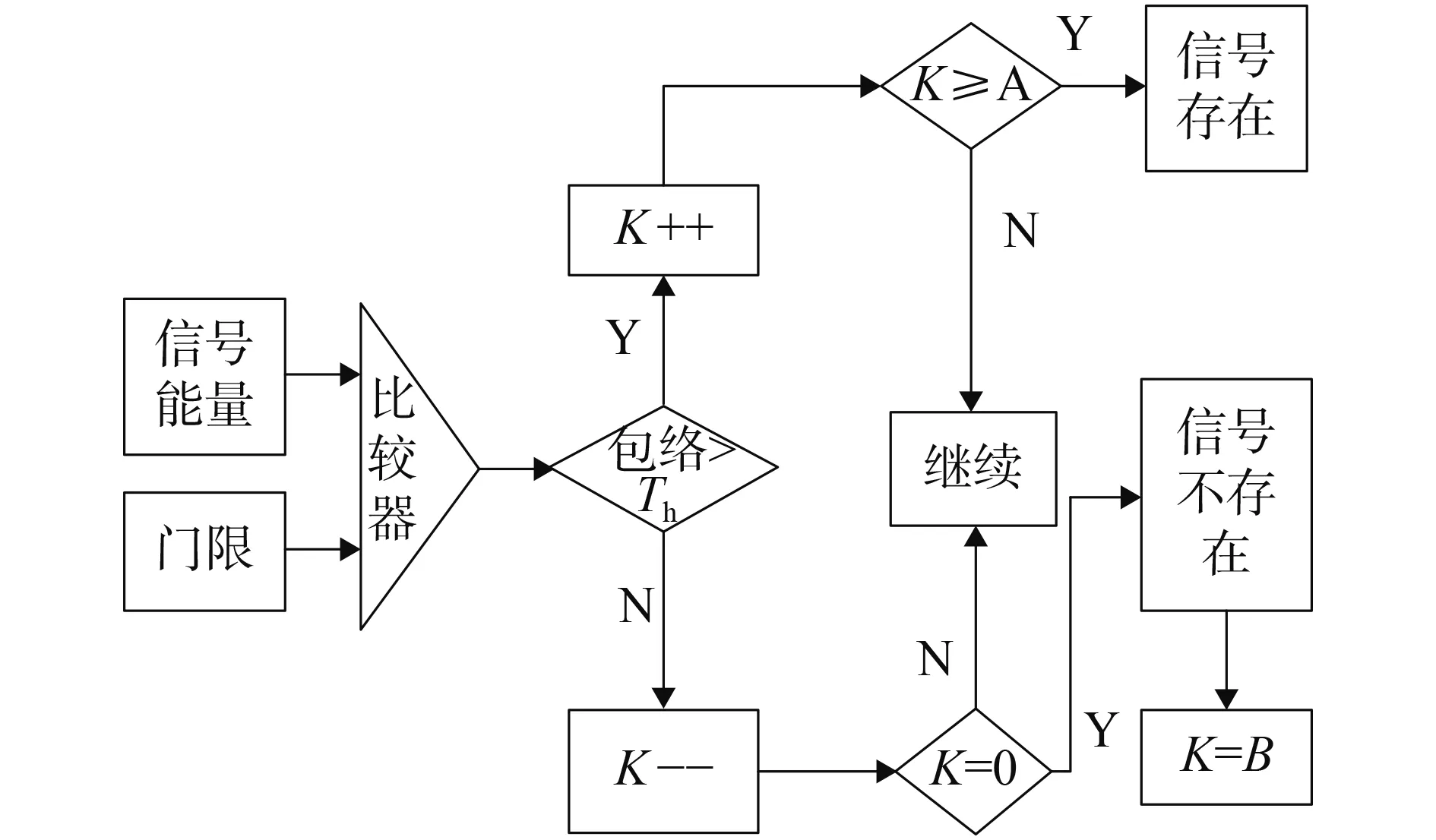
圖3 唐檢測器檢測算法流程Fig.3 Tong detection algorithm flow

圖中Th為單次比較的門限值。可以看出唐檢測算法是一種可變檢測次數的檢測器，其檢測滿足兩個吸收壁的隨機游動過程，系統虛警概率[4-5]為

(3)

系統檢測概率[6-7]為

(4)

駐留次數的平均數目為[8]

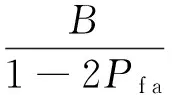
(5)

唐檢測算法的仿真結果如圖4和表2所示。

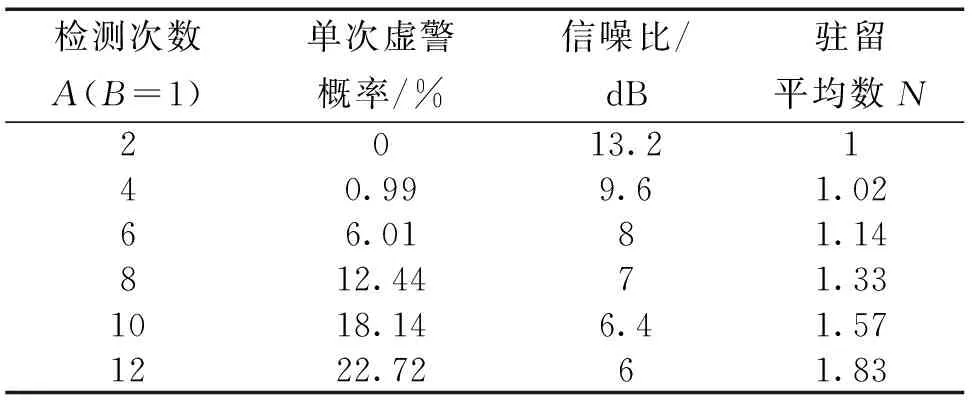
表2 唐檢測器檢測性能

圖4 唐檢測器檢測算法仿真結果Fig.4 Simulation results of Tong detection algorithm

從圖4和表2中可以看出，A的增大提高了系統檢測概率，降低了對信號信噪比的要求，但付出的代價是降低了搜索速度。因而A的選擇是在搜索速度和檢測概率之間的折中。唐檢測算法的缺點是在特定的弱信號條件下，檢測器會長時間滯留在某個捕獲結果的檢測確認過程中。

1.3改進的檢測算法

基于上述兩種算法，本文提出了一種改進算法，使得強信號盡早確認成功，不存在的衛星信號也能很快得到剔除。

首先根據不同的單次虛警概率，針對信號存在和不存在兩種情況，設定相應的多個門限。一種實施方法如表3所示。在信號存在時設置5個門限用于確認，在信號不存在時設置2個門限用于剔除。

表3不同虛警概率對應的預設定門限示例

Table3Pre-setthresholdscorrespondingtothedifferentfalsealarmprobability

門限類型虛警概率/%門限信號存在時的檢測門限信號不存在時的剔除門限1TH-E10.1TH-E20.01TH-E30.001TH-E40.0001TH-E51TH-NE110TH-NE2

然后將信號與各個門限依次進行比較，比較結果每大于信號存在時的5個門限中的1個，計數器J加1，當J不小于N時檢測成功。比較結果每小于信號不存在時的2個門限中的1個，計數器K減1，當K=0時檢測失敗。其中J初始值取0，K初始值取L，算法流程如圖5所示。

在強信號存在條件下，信號有極大概率可一次性大于所有的5個確認門限，滿足J=N，實現單次駐留即檢測成功，避免了N中取M算法中強信號依然需要檢測N次的缺點。在弱信號存在條件下，信號僅大于少數較小的門限時，需要經過多次駐留檢測后滿足J不小于N時才檢測成功，避免了唐檢測算法中弱信號會導致計數器反復加減，長時間滯留的情況。在信號不存在的條件下，信號小于剔除門限時，會很快被剔除。綜合上述3種情況，改進算法的檢測速度會得到有效提升。

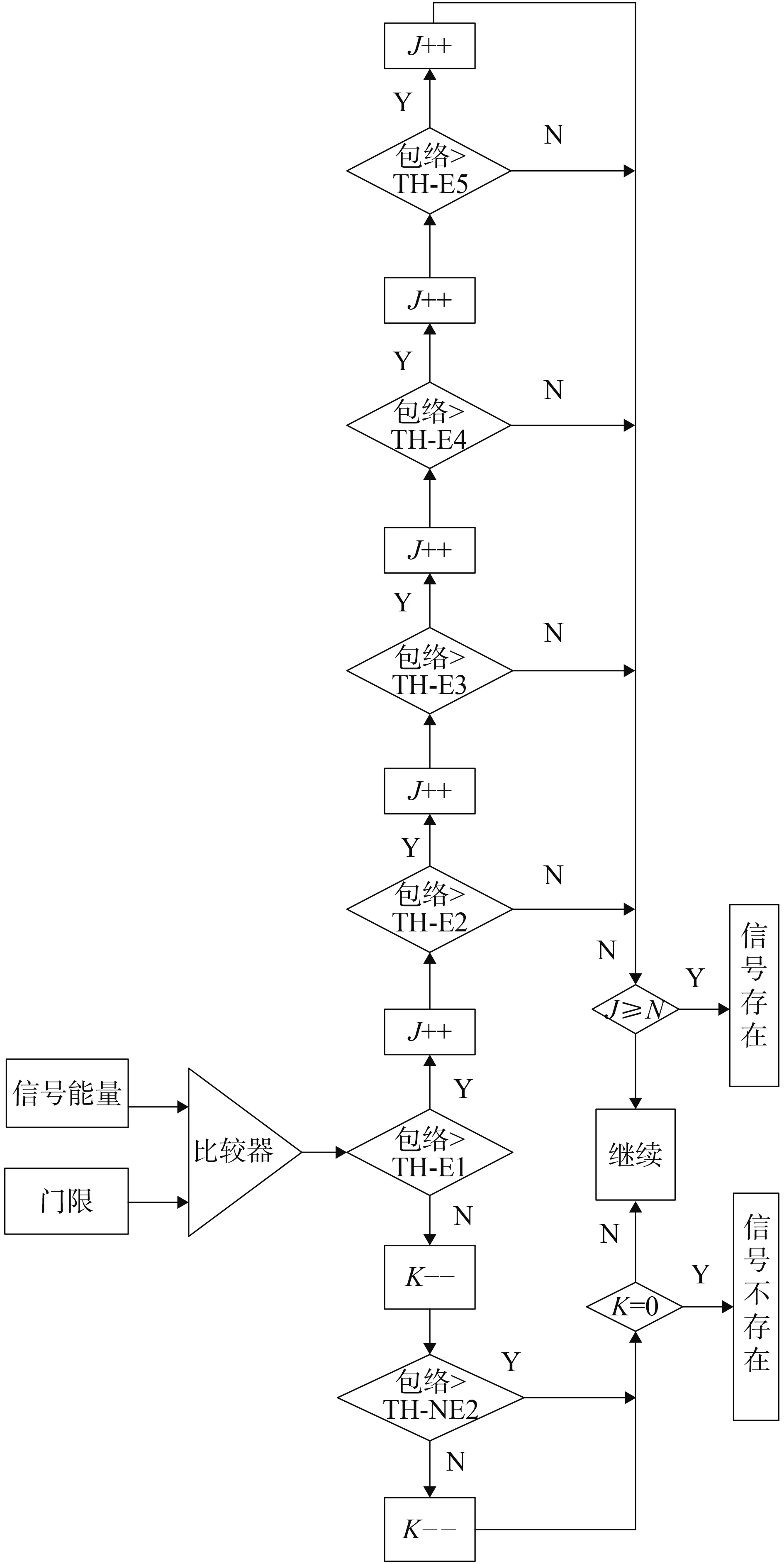
圖5 改進檢測算法流程圖Fig.5 Improved detection algorithm flow

接收機天線接收到的衛星信號經過相關器解調、解擴和積分清零之后的I、Q兩路1ms相干積分結果為

I=Asinc(ΔfmT)R(τ)Dcos(ΔΦ)+ni

(6)

Q=Asinc(ΔfmT)R(τ)Dsin(ΔΦ)+nq

(7)

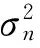
單次非相干積分包絡為

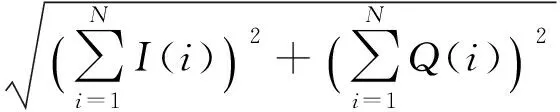
(8)

當信號不存在時，I與Q服從均值為0，方差為σ02的高斯分布。此時x為噪聲的積分，服從Rayleigh分布[9]；x的均值與方差為

(9)

(10)

當信號存在時，x服從Rice分布[9]，其非中心參量為

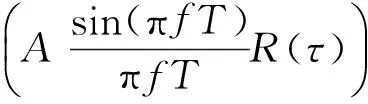
(11)

此時x的均值與方差為

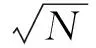
(12)

D(x/H1)=N(2σ02+s2)-[E(x/H1)]2

(13)

式中：H0、H1分別表示信號不存在和存在兩種情況；I0、I1分別為零階和一階貝塞爾函數；γ1=s2/(2Nσ02)。

經過M次非相干積分之后可以得到檢測量y：

(14)

由中心極限定理可知，當非相干積分時間很大時，非相干積分累加值服從高斯分布，可以用高斯分布進行近似求解[9]。

y的均值與方差分別為

E(y)=M·E(x)

(15)

D(y)=M·D(x)

(16)

根據高斯分布積分函數可以求出虛警概率為

(17)

式中：erfc(x)表示互補誤差函數。根據已知的虛警概率，可以求得相應的門限值：

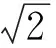
(18)

式中：erfc-1(x)表示互補誤差函數的逆函數。根據高斯分布積分函數可以求出檢測概率為

(19)

由于設置了多個判決門限，導致系統虛警概率和檢測概率難以獲得解析解，因此在下一節將采用蒙特卡洛方法分析算法的性能。

2 檢測算法測試結果

2.1測試數據與方法

測試數據由思博倫GSS 9000信號模擬器產生，使用思博倫GSS 6425記錄回放系統采集所需不同信號強度的中頻數據。

使用測試數據對上文提到的3種檢測確認算法進行測試。考慮不同算法參數、碼相位初始偏差和多普勒頻率初始偏差對檢測算法測試結果的影響。本文采用的捕獲引擎其捕獲結果碼相位偏差最大為半個碼片，多普勒頻率偏差最大為200 Hz。

對同一中頻數據進行分析，具體的測試方法為：首先考慮不同碼相位偏差對測試結果的影響，通過采樣點偏移來模擬碼相位偏差，即每次略過不同的起始采樣點進行多次測試。本文中頻采樣率取16.368 MHz，半碼片速率2.046 MHz，即8個采樣點對應1.5碼片偏差。在測試時，采用從起始偏移1個采樣點直到偏移8個采樣點來進行測試，這樣可以完全覆蓋一個半碼片的偏差。然后考慮多普勒偏差的影響，在獲取該中頻信號某顆衛星的真實多普勒值后，在該值上增加或減少某個固定頻率值來模擬不同多普勒偏差對測試造成的影響。最后，每次仿真的數據量需要滿足蒙特卡洛的測試要求，如要達到0.01的準確率，仿真的個數至少需要104量級。

測試捕獲檢測性能時，為了體現檢測算法的性能，這里將捕獲檢測分為二級檢測，第一級采用最大值檢測[10]：對碼相位和頻率進行二維捕獲，得到的捕獲結果取最大值與門限比較進行一級檢測。捕獲第二級檢測則采用檢測算法進行判斷，這里主要對本文提到的三種檢測算法進行比較分析。從檢測算法的參數、初始多普勒偏差的影響、信號存在和信號不存在時的檢測概率、虛警概率和捕獲速度，不同信號強度和不同積分時間的影響這幾方面進行測試和驗證。

2.2不同檢測算法參數的選擇

表4給出了一組不同參數下的測試結果，用于測試不同參數下的檢測算法性能。測試條件為：數據信號強度-126 dBm，捕獲積分策略為2 ms相干積分，1次非相干積分。

表4 不同算法參數下的檢測結果

由表4可以看出：

1)唐檢測器B=2時的檢測性能要優于B=1時的性能，這是因為B=1時，很容易產生漏警。

2)唐檢測器B=2時，A越小，對應的檢測速度越快，且與A較大時的檢測概率基本一致。從性能上來看B=2，A=5性能最優且檢測速度最快。

3)改進算法中L=3要優于L=1，檢測概率較高。

4)由測試結果可看出，改進檢測算法性能最優，一方面檢測概率高，另一方面檢測速度快。

此外，采用了不同信號強度的數據進行了對比驗證，結果與-126 dB·m信號結果的一致性良好。

充灌程序采用自下至上的充灌方法，模袋在充灌進混凝土后，模袋布會出現膨脹拉緊，此時需調整上口邊固定槽鋼的拉緊葫蘆，做好張力放松工作，以防模袋灌注不飽滿。整塊袋布灌注結束后，取出固定鋼管，清洗泵車及管道。

為了使3種檢測算法有可比性，在上述結果中挑選各個算法性能最佳的參數：N中取M檢測算法取N=8，M=5；唐檢測算法取A=5，B=2；改進檢測算法取N=5，L=3。

2.3信號存在時多普勒頻偏對檢測性能的影響

采用信號強度為-126 dB·m的信號，捕獲積分策略采用2 ms相干積分，1次非相干積分進行檢測，捕獲最大值初級檢測的檢測概率為81.8%，測試結果如表5所示。

表5信號存在條件下不同多普勒偏差的測試結果

Table5TestresultsindifferentDopplerdeviationwhensignalsexist

檢測算法多普勒偏差/Hz0125-70-200檢測概率/%平均檢測次數檢測概率/%平均檢測次數檢測概率/%平均檢測次數檢測概率/%平均檢測次數8中取599.888.0099.198.0099.828.0095.378.00唐檢測算法99.922.8899.573.0099.832.9097.43.36改進算法99.942.0699.622.1399.882.1397.912.82

由表5可以看出：

1)二級檢測中的3種檢測算法，在不同多普勒偏差下，檢測概率均達到95%以上，表明這幾種檢測算法均能滿足捕獲檢測概率達到90%以上的要求。

2)隨著多普勒偏差為0～-200 Hz，3種檢測算法對應的檢測概率均有下降，平均檢測次數均有增加。

2.4信號不存在時的剔除速度

下面分析當信號不存在時，3種檢測算法對應的性能。

當信號不存在時，對-128 dB·m數據采用2 ms相干積分，1次非相干積分策略，捕獲不存在的衛星，得到的結果如表6所示。

表6 信號不存在條件下測試結果

從表6可以看到3種算法的虛警概率都為0，滿足了系統虛警概率10-6的要求。在檢測速度方面，改進算法在N=5，L=3條件下的剔除速度略優于唐檢測，在L=2時明顯更快。因此改進算法不僅可以應用到信號存在時的確認過程，同時也可以應用到信號不存在時的剔除過程，既能保證信號的檢測概率和虛警概率，也能保證檢測速度。

2.5不同信號強度下的算法性能測試

分兩方面對檢測算法性能進行測試，信號存在時的檢測概率和信號不存在時的剔除概率。

首先分析信號存在時的檢測結果，對應不同衛星信號強度，采用不同的積分策略，只捕獲存在的衛星，測試結果如表7所示。其中檢測條件一為：-131 dB·m,2×3積分策略，最大值檢測概率為88.73%；條件二為：-131 dB·m,2×3積分策略，最大值檢測概率為68.53%；條件三為：-133 dB·m,2×7積分策略，最大值檢測概率為89.31%；條件四為：-134 dB·m,2×7積分策略，最大值檢測概率為83.41%。從表7可以看出：

1)當捕獲最大值檢測一級檢測的檢測概率達到80%以上時，捕獲檢測確認二級檢測的這幾種檢測算法對應的檢測概率均達到99%；當最大值檢測一級檢測的檢測概率下降到70%時，捕獲檢測確認二級檢測的檢測概率仍能達到97%的性能。3種檢測算法均滿足需求。

2)從檢測概率，漏檢概率和虛警概率的性能來看，這幾個檢測算法基本一致，相差不大。但是改進算法平均檢測次數最少，速度相對于N中取M能提高3倍，相對于唐檢測算法能提高1/3。

接著分析不同信號強度下，信號不存在時的檢測性能。測試時選擇不存在的2號衛星進行捕獲，結果如表8所示。從表8可以看到信號不存在時，針對不同信號強度，這幾種檢測算法都能準確的剔除。但改進算法的剔除速度最快，性能最優。

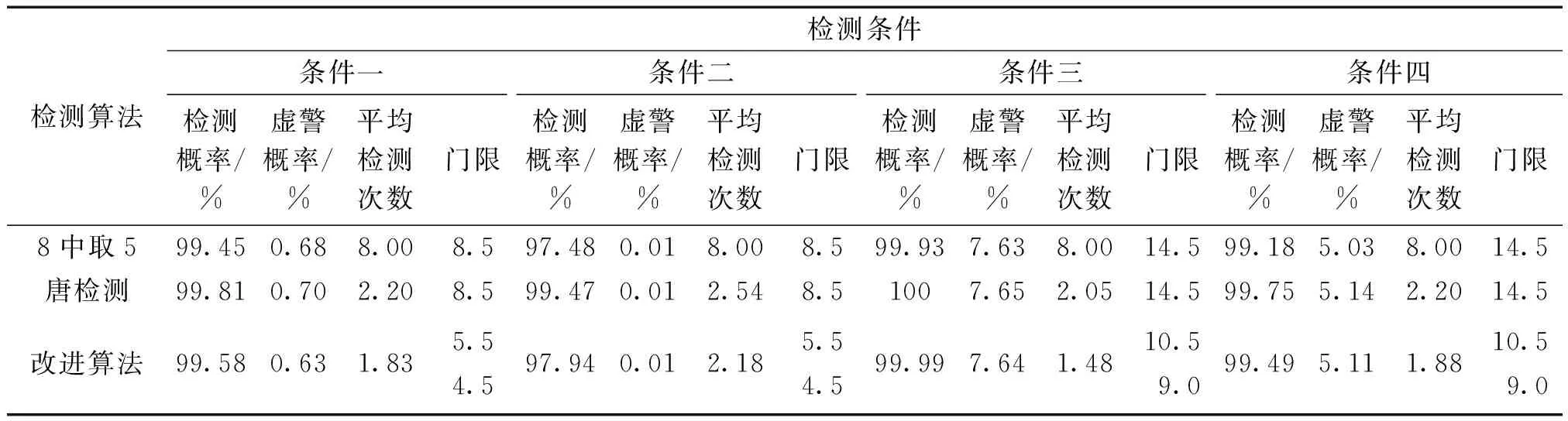
表7 不同信號強度下信號存在時的檢測結果

表8 不同信號強度下信號不存在時的檢測結果

3 結論

1)檢測確認算法的二級檢測受初始多普勒偏差影響，隨著多普勒偏差的加大，對應檢測算法的檢測概率變小，平均檢測次數增加。

2)不同信號強度下，當信號存在時，3種算法的檢測概率基本相同且都滿足系統要求，但是從平均檢測次數來看，改進算法最優，速度相對于N中取M能提高3倍，相對于唐檢測算法能提高1/3。當信號不存在時，3種算法的虛警概率都接近0,，滿足系統要求，但改進算法的剔除速度略優于其他兩種方法。說明改進的多門限檢測判決不僅可應用到信號檢測確認部分，同時也可應用到信號不存在時的剔除過程。

3)檢測算法比較結論：在不同多普勒初始偏差和不同信號強度條件下，3種不同檢測算法仿真結果說明，改進算法在檢測概率虛警概率沒有任何損失的情況下檢測速度具有明顯優勢。

[1] 謝鋼. GPS原理與接收機設計[M]. 北京：電子工業出版社, 2009: 358-362.

XIE Gang. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2009: 358-362.

[2] KAPLAN E D, HEGARTY C J.GPS原理與應用[M]. 2版. 寇艷紅譯. 北京: 電子工業出版社, 2007: 223-227.

KAPLAN E D, HEGARTY C J. Understanding GPS principles and applications[M]. 2nd Ed. Beijing: Publishing House of Electronics Industry, 2007: 223-227.

[3] WARD P W. GPS receiver search techniques[C]//Proceedings of the IEEE 1996 Position, Location, and Navigation Symposium. Chicago, USA, 1996: 604-611.

[4] TONG P S. A suboptimum synchronization procedure for pseudo noise communication systems[C]//National Telecommunications Conference. Atlanta, USA, 1973: 26D-1-26D-5.

[5] 馬琳, 崔嵬, 吳嗣亮. 極低信噪比環境下含近鄰約束的改進唐檢測判決算法[J]. 系統工程與電子技術, 2011, 33(8): 1745-1749.

MA Lin, CUI Wei, WU Siliang. Improved Tong multiple trial algorithm with near neighbor constraint in extremely low SNR condition[J]. Systems engineering and electronics, 2011, 33(8): 1745-1749.

[6] 馬琳, 崔嵬, 田靜,等. 基于馬爾可夫鏈的含有檢測次數約束條件的唐檢測器[J]. 宇航學報, 2011, 32(8): 1799-1804.

MA Lin, CUI Wei, TIAN Jing, et al. Study on Tong detector with number of detection times constraint based on Markov chain[J]. Journal of astronautics, 2011, 32(8): 1799-1804.

[7] 朱云龍, 丑武勝, 楊東凱. Tong檢測算法性能分析及參數設置[J]. 北京航空航天大學學報, 2015, 41(3): 418-423.

ZHU Yunlong, CHOU Wusheng, YANG Dongkai. Performance analysis and parameter setting for Tong detection algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 418-423.

[8] 李思超，葉甜春，徐建華. 唐檢測器的駐留時間及檢測性能分析[J]. 電子測量技術, 2009, 34(3): 53-55.

LI Sichao, YE Tianchun, XU Jianhua. Analysis on resident time and detection performance of tong detector[J]. Electronic measurement technology, 2009, 34(3): 53-55.

[9] PROAKIS J G.數字通信[M]. 4版. 張力軍譯. 北京: 電子工業出版社, 2003: 29-31.

PROAKIS J G. Digital communications[M]. 4th Ed. Beijing: Publishing House of Electronics Industry, 2003: 29-31.

[10] 歐松林，李金海.GNSS系統中檢測與判決的研究[J]. 計算機工程與設計, 2014, 35(3): 741-745.

OU Songlin, LI Jinhai. Study on detection and decision of GNSS system[J]. Computer engineering and design, 2014, 35(3): 741-745.

本文引用格式：張超逸，曾丹丹，李金海，等. 一種改進的GNSS信號快速捕獲檢測算法[J]. 哈爾濱工程大學學報， 2017， 38(10): 1609-1615.

ZHANG Chaoyi, ZENG Dandan, LI Jinhai, et al. An improved algorithm for rapid detection in acquisition of GNSS signal[J]. Journal of Harbin Engineering University， 2017， 38(10): 1609-1615.

ImprovedalgorithmforrapiddetectioninGNSSsignalacquisition

ZHANG Chaoyi, ZENG Dandan, LI Jinhai, SUN Jinhai, YAN Yuepeng

(Institute of Microelectronics， Chinese Academy of Sciences, Beijing 100029, China)

To ensure fast acquisition of satellite signals in high dynamic applications, an improved algorithm was proposed for signal detection during acquisition by global navigation satellite system. The algorithm combined the advantages of theM-of-Nand Tong detection algorithms. Through the multi-threshold detection mechanism, the detection and rejection speed accelerated whether the signals exist or not. Numerous real data tests show that the improved algorithm is three times faster than theM-of-Ndetection algorithm and one-third times faster than the Tong detection algorithm without any performance deterioration.

satellite navigation receiver; high dynamic; fast acquisition; GNSS;M-of-Ndetection algorithm; Tong detection algorithm; multi-threshold detection; detection speed in acquisition

10.11990/jheu.201605079

http://www.cnki.net/kcms/detail/23.1390.U.20170816.1445.010.html

TN911.23

A

1006-7043(2017)10-1609-07

2016-05-23. < class="emphasis_bold">網絡出版日期

日期：2017-08-16.

國家自然科學基金項目(61271423).

張超逸(1990-), 男,博士研究生;閻躍鵬(1964-), 男,研究員,博士生導師.

張超逸，E-mail: zhangchaoyi@ime.ac.cn.