串聯冗余自由度機構關節角位置的規劃算法

吳鵬，洪娟，陳廣，徐博

(1.哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001； 2.北京航天控制儀器研究所，北京 100854)

串聯冗余自由度機構關節角位置的規劃算法

吳鵬1，洪娟2，陳廣1，徐博1

(1.哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001； 2.北京航天控制儀器研究所，北京 100854)

為了建立一種實時求解串聯冗余自由度機構關節角位置的方法，解決串聯冗余自由度機構逆運動學求解中角位置的求解問題，給出了逆運動學的數值解。根據加權偽逆理論，采用瞬時最優速度表達關節空間角增量的方法，研究了關節空間角位置數值解法，給出了冗余自由度機構連續跟蹤期望空間姿態時的關節空間角位置計算方法。在典型運動輸入條件下，分別恒定速比關節位置算法和加權逆速度積分方法獲得的關節位置和姿態誤差進行仿真。為驗證算法有效性，以衛星天線姿態穩定系統為研究對象，仿真結果表明，恒定速比關節位置算法在運動學逆解過程中能夠保證天線姿態誤差Frobenius(弗羅貝尼烏斯)范數小于10-4。仿真結果表明：本文提出的方法能夠連續給出冗余自由度機構運動過程中的關節空間角位置的希望值，實現了逆運動學角位置層面的數值解和理想的控制精度。

冗余自由度機構； 衛星天線； 加權偽逆； 逆運動學； 運動規劃； 恒定轉速比； 關節角位置； 姿態穩定； 姿態誤差； Frobenius范數

船舶在海上航行或無人飛行器執行遠距離任務時，與陸地或指揮中心的通信都需要依靠地球同步通信衛星。上下行信號的傳送，需要天線接收主瓣指向衛星，同時天線的極化方向與衛星發射信號的極化方向需要保持一致[1]。因此天線姿態穩定系統被廣泛使用，實現衛星天線與地球同步衛星之間的相對穩定。接收天線主瓣方向與極化方向之間是垂直的，利用這兩個方向構成了一個來描述天線姿態的坐標系。理論上，坐標系在空間的定點轉動有3個自由度，具有3個正交自由度的運動機構就可以實現天線姿態的伺服。現實中，為了克服運動機構奇異點問題，增加系統靈活性，采用具有4個正交運動軸的框架結構，本文研究對象是一個冗余自由度的天線姿態穩定系統。

聯接天線與運載器的穩定系統將實現了天線相對于運載器的姿態運動，同時也建立了天線姿態與穩定系統關節空間的約束。對與任務空間而言使用n維向量X，X∈Rn描述規劃的任務；對于關節空間，使用m維向量Θ，Θ∈Cm描述關節變量。當m>n時系統即為冗余自由度系統，可以實現關節的避障、克服奇異點、完成第二任務等要求，例如實現機器人更好的靈活性[2-3]，躲避障礙[4-7]、防止關節運動超界[8-11]、避免奇異性[12-15]、減小關節運動速度及優化動力學性能等[16-17]。對于本文中的姿態隨動系統，當系統自由度為m=4時，形成姿態冗余自由度系統。對于冗余自由度機器人而言，運動學逆解有無窮多組。從無窮多組解中選擇合適解的過程，也就是冗余自由度問題的求解過程。成果包括：幾何求解方法[18-19]；Pieper證明了對于連續3個軸交于一點的冗余自由度機構，一定具有解析解[20]；Liegeois及梯度投影法把冗余自由度問題的逆解分為了特解和齊次解，利用關節的自運動實現冗余自由度機器人的次任務[21-23]；Whitney最早采用了這種廣義逆形式來求取一般機器人的逆運動學及軌跡規劃問題，獲得了關節角速度向量的模最小解，也成為基于速度層面求解冗余自由度問題的基礎[24]；Wampler最早提出了加權最小二乘法實現主任務與自運動的同步完成[25]；Lee和Badler提出了可以選擇合適的關節角度作為參數，表示其余的角度，進行解析解的求解方法[26-27]。

以上方法中，除幾何方法和文獻外，主要集中在對關節空間的速度求解，對于關節空間的位置求解研究較少，在對于機構末端軌跡有高精度要求的應用場合，并不適用[19]。

本文提出了一種建立在加權偽逆速度解基礎上的恒定速比關節位置算法，使用該方法直接計算得到關節空間中的角位置值，計算誤差不累計，能夠保證天線姿態在運動過程中達到期望精度。

1 姿態穩定系統的描述

運載器、天線、穩定系統和衛星之間相互姿態關系與各坐標系的定義如圖1所示。圖1中，建立當地地理坐標系為東北天坐標系XeYeZe；運載器坐標系為與其固聯的前右上坐標系XbYbZb；與天線固連的坐標系為XaYaZa，其中Za為天線接收主波瓣方向，Ya為天線極化方向；建立與衛星固聯的坐標系XsYsZs，其中Zs為衛星發射信號主瓣的相反方向，Ys為衛星發射天線極化方向。

天線姿態穩定問題等效于將天線本體坐標系XaYaZa穩定在地理坐標系XeYeZe中，當運載器坐標系XbYbZb發生變化時，通過穩定系統的伺服運動，保證坐標系XaYaZa與衛星固聯坐標系XsYsZs的一致。

圖1 運載器、天線及衛星坐標系相互關系描述圖Fig.1 Description of the relationship between carrier, antenna and satellite coordinate system

設每次一轉動的姿態轉移矩陣分別為T1、T2、T3和T4，而每一個姿態轉移矩陣又僅與一個對應的關節角度有關，得到運載器坐標系與天線本體坐標系之間的姿態轉移矩陣為

bTa=T1·T2·T3·T4=f(θ1,θ2,θ3,θ4)

(1)

式中：θ1～θ4為姿態穩定系統的4個運動軸角度值。嘗試建立圖1中各坐標系之間的轉換關系，這里用姿態轉移矩陣eTb表示坐標系XbYbZb在坐標系XeYeZe中的表達。同理利用姿態轉移矩陣寫出各坐標系之間轉換關系為

bTs=bTe·eTs=bTa

(2)

式中：eTs為衛星在地理坐標系下的表示，對于給定的地球同步衛星目標，在地球上某一點觀察衛星，可以認為eTs保持不變；eTb為運載器在地理坐標系下的表示；bTa為天線在運載器坐標系下的表示；運載器運動，eTb發生變化，系統完成的功能就是調整θ1～θ4，更新bTa使得(2)式保持成立[1]

bTa=bTe·eTs=N(t)

(3)

式中：將衛星在運載器坐標系下的連續運動用矩陣序列N(t)表示。則本文問題轉化為如何在如式(4)的約束條件下，進行冗余自由度機構逆運動學求解。

f(θ1,θ2,θ3,θ4)=N(t)

(4)

矩陣N(t)的值則可通過姿態的運動和衛星參數求得：

這里假設衛星方位角度為Ae，俯仰角度為Ee，極化角約定為繞衛星姿態矩陣Zs軸經過σe的轉動后，使得Ys軸與地面平行，此時的σe為極化角，并約定極化角正方向為逆時針方向，且確定極化角時以坐標系的Ys軸正方向為準。ψ為運載器航向角，φ為運載器的縱搖角，γ為運載器的橫搖角。

2 加權意義下的速度最優解

2.1雅克比矩陣的建立

天線姿態穩定是一個姿態跟蹤控制過程。將初始條件位置時刻定義為t0時刻，此時的天線姿態矩陣為N(t0)。隨著運載器運動，在t1時刻運載器坐標系下的天線姿態應更新至N(t1)，在任意時刻姿態矩陣為N(tn)。根據機構的約束關系有：

f(Θn)=N(tn)

(5)

Θn=f-1(N(tn))

(6)

對于式(6)所描述的冗余自由度運動學逆解，f-1(·)代表函數f(·)的反函數。利用系統的Moore-Penrose的廣義逆[24](簡稱M-P逆)可求得速度層面的最優解，本文中提出的恒定速比關節位置算法也是從偽逆速度的角度出發的。首先建立由雅克比矩陣J描述的關節運動與天線姿態運動的關系為

(7)

2.2天線坐標系的轉動速度

在前節中已經獲得了衛星姿態的描述矩陣eTs，且通過慣性測量單元得到了t時刻的運載器姿態的歐拉角，求得了eTb。利用式(2)直接得到連續變化的矩陣序列N(t)。對于任意相連時刻的N(tn)和N(tn+1)=N(tn+Δt)有：

N(tn+Δt)=Rot(q,dθ)N(tn)

(8)

式中：

Rot(q,dθ)=Rot(x,δx)Rot(y,δy)Rot(z,δz)

(9)

Rot(q,dθ)代表坐標系繞某一個軸q轉動了dθ角度，Δt為兩次測量測量之間的時間間隔；Rot(x,δx)為繞當前坐標系的x軸轉動δx的微分運動，相應地Rot(y,δy)和Rot(z,δz)為繞另外兩個軸的微分運動。當δx、δy和δz較小時，忽略二階小量可得

(10)

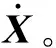
2.3瞬時關節最優速度求解

許多文獻針對冗余自由度機構在速度層面的解進行了深入的探討，其中具有加權M-P逆解具有各關節同步運動，無關節自運動的特點，本文選用此方法作為關節速度的逆解方法[25]。對于四軸穩定系統，第1～4軸所消耗的能量逐漸減小，按照權值系數逐步降低的原則為轉動關節分配轉動權值，建立權值向量

(11)

此時的關節速度可表示為

(12)

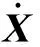
3 恒定速比位置更新方法

3.1姿態跟蹤系統的特點

姿態跟蹤系統處在另外一種情況，一方面對于末端姿態精度有較高要求；另一方面，在給定一個期望姿態的情況下，希望系統夠以最快的速度實現姿態更新，實現對目標位置。

對于姿態跟蹤系統，姿態測量單元每秒更新20～50次姿態信息，每個更新的姿態信息對應姿態矩陣序列N(t)中的一個矩陣。每當新的姿態矩陣出現，要求跟蹤系統能夠盡可能快速地實現天線姿態與期望姿態N(t)的一致。對于兩個姿態矩陣之間的姿態轉移過程則不關注，不需要對兩個姿態之間的軌跡做精確規劃，而是將關注的重點放在對應每一個期望姿態所對應的關節角上，即對式(6)快速求解的方法，獲得運動學逆解。

3.2現有方法的不足

2)姿態跟蹤系統的控制不同于離線規劃或示教方式規劃的機器人系統，后者可以根據精度要求詳細地規劃軌跡上的每一個點。姿態跟蹤系統關注的是期望姿態的快速建立和姿態建立精度，而對于給定的期望姿態如何直接求解關節的角位置尚沒有成熟的方法。雖然可以建立姿態誤差的反饋，多次計算偽逆，直至末端位姿滿足精度要求。但計算量大，收斂速度慢，不適合進行在線規劃。

3.3恒定速比位置算法

本文提出了一種基于關節最優速度比恒定和姿態約束方程的關節位置算法，簡稱為恒定速比(CRR)位置算法。

對于給定末端坐標系運動速度，基于式(12)可獲得關節瞬時最優速度。冗余自由度最優速度意義本質上是將末端姿態運動合理地分解到各運動關節。角位移是有角速率和運動時間決定的，在相同的采樣時間間隔上，如果角速率保持不變，那么關節空間角位移將正比于角速率。各軸的瞬時速率值，也代表了各軸瞬時角度運動量的大小。各關節瞬時速度之比，即瞬時關節運動量之比。將姿態轉移過程中關節運動速度比設定為恒定，即恒定速比，是本文算法的核心思想。將每一個關節的運動速度通過某一個關節運動速度和關節之間速度的比值關系表示，并設定這一速比關系在每一次姿態轉移過程中保持恒定。通過這樣的表達，可以將采樣周期內關節角位置增量表達出來，將這個待求角度增量的表達式直接帶入姿態約束方程，求得每個關節角的增量值，進而獲得關節角位置。

將此方法應用于天線姿態穩定系統，求解關節角位置的步驟為：

1)根據衛星的參數，計算矩陣eTs；

2)與運載器固連的姿態測量單元檢測到運載器的運動姿態，利用歐拉角ψ、φ和γ描述航向角、縱搖角和橫搖角，計算得到bTe，結合eTs求得此時衛星在運載器坐標系下的姿態矩陣記為N(tn+1)，相應的前一時刻的姿態矩陣記為N(tn);

3)在工作空間中進行運動微分的提取。計算連續兩個位姿轉動之間的差值，即兩位姿之間的姿態轉移矩陣為

N(tn+1)=Rot(q,dθ)N(tn)

(13)

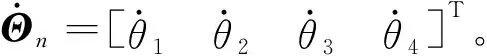
(14)

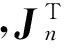
5)根據建立的關節空間變量與工作空間之間的關系，在第n次姿態測量的時刻，有：

f(Θn)=N(tn)

(15)

那么對于tn+1有：

f(Θn+1)=f(Θn+ΔΘ)=

f(Θn+Φ·Δt)=N(tn+1)

(16)

6)建立恒等速比的關系式為

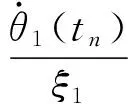
(17)

利用第一軸表示其余軸的速度，有：

(18)

式中:k2、k3、k4為關節速度比例系數，在單次關節位置計算過程中保持不變，即保持恒定速比。關節增量表達式可寫為

(19)

7)將式(18)的增量表達式代入式(15)的方程中，將Θ作為初始，利用牛頓迭代方法即可獲得ξ1。將ξ1代入式(19)，求得ΔΘ。

將算法總結為流程圖，如圖2所示。

圖2 恒定速比位置更新算法流程圖Fig.2 Flow chart of CRR position update algorithm

4 姿態穩定系統運動仿真結果

4.1仿真條件

本文為了驗證算法在運載器大動態特性下的結果，設定了一個跟蹤目標，并仿真運載器的運動規律，觀察關節空間的運動情況及末端位姿的誤差。仿真時間間隔為ΔT=0.01 s。

對跟蹤目標做如下假設：目標方位角度：223.49°，俯仰角：60°，極化角度：-28.8°。按照本文中建模規則，初始位置下目標對應的關節角度為

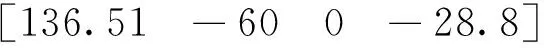
(20)

運載器的航向角、縱橫搖角運動組照如下的描述為

ψ=40sin[(2π/30 000)t]+0.01t

φ=40sin[(2π/800)t]

γ=45sin[(2π/1 000)t]

(21)

4.2偽逆方法仿真結果

按照仿真條件，分別使用恒等速比方法和加權M-P逆方法進行了穩定系統關節角、關節角速度和姿態誤差的計算。

直接利用關節角速度積分或的關節角位置，如圖4所示。

將計算得到的各關節角度帶入運動學方程計算，獲得末端的姿態矩陣，將此姿態矩陣與期望姿態矩陣進行做差，計算差矩陣的Frobenius范數值，如圖5所示。

可以看到單純利用偽逆速度積分獲得的末端姿態矩陣誤差會快速發散。

使用恒定速比方法進行計算，計算結果為每一步的關節角更新位置，直接獲得關節角位置變化曲線如圖6所示。

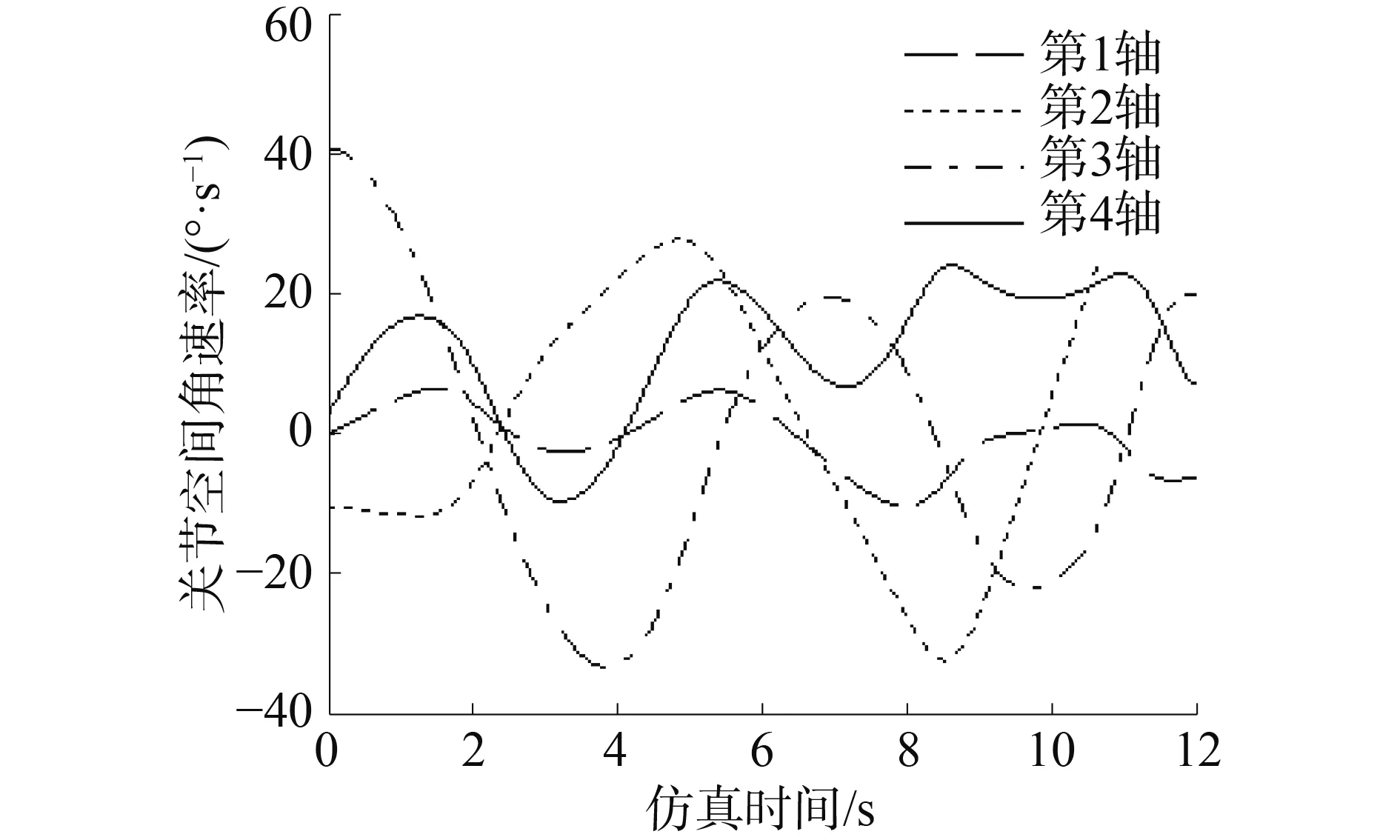
圖3 根據M-P逆求得的各軸速度值Fig.3 The solution of joints velocity based on the M-P inverse

圖4 對M-P逆生成速度進行積分得到的角度值Fig.4 The joints values obtained by using M-P inverse velocity integral

圖5 姿態誤差矩陣Frobenius范數值Fig.5 Frobenius norm values of attitude error matrix

本文解決的重點在關節空間角位置的計算，暫時不考慮關節的限位問題。在恒定速比方法求解過程中每一步計算得到的M-P逆速度如圖7所示。

同樣地根據各關節角度值進行運動學正計算，將獲得姿態與期望姿態進行做差，求得誤差矩陣的Frobenius范數曲線如圖8所示。由于是利用恒速比方法直接求得的位置值，關節角的速度值是通過位置差分得到的平均速度值，差分結果如圖9所示。

圖6 利用本文的恒速比方法獲得角度值Fig.6 The joints values obtained by using RCC approach

圖7 恒速比方法中的各關節的M-P逆轉速值Fig.7 The M-P inverse velocity of joints in RCC approach

圖8 姿態誤差矩陣Frobenius范數值Fig.8 Frobenius normal values of attitude error matrix

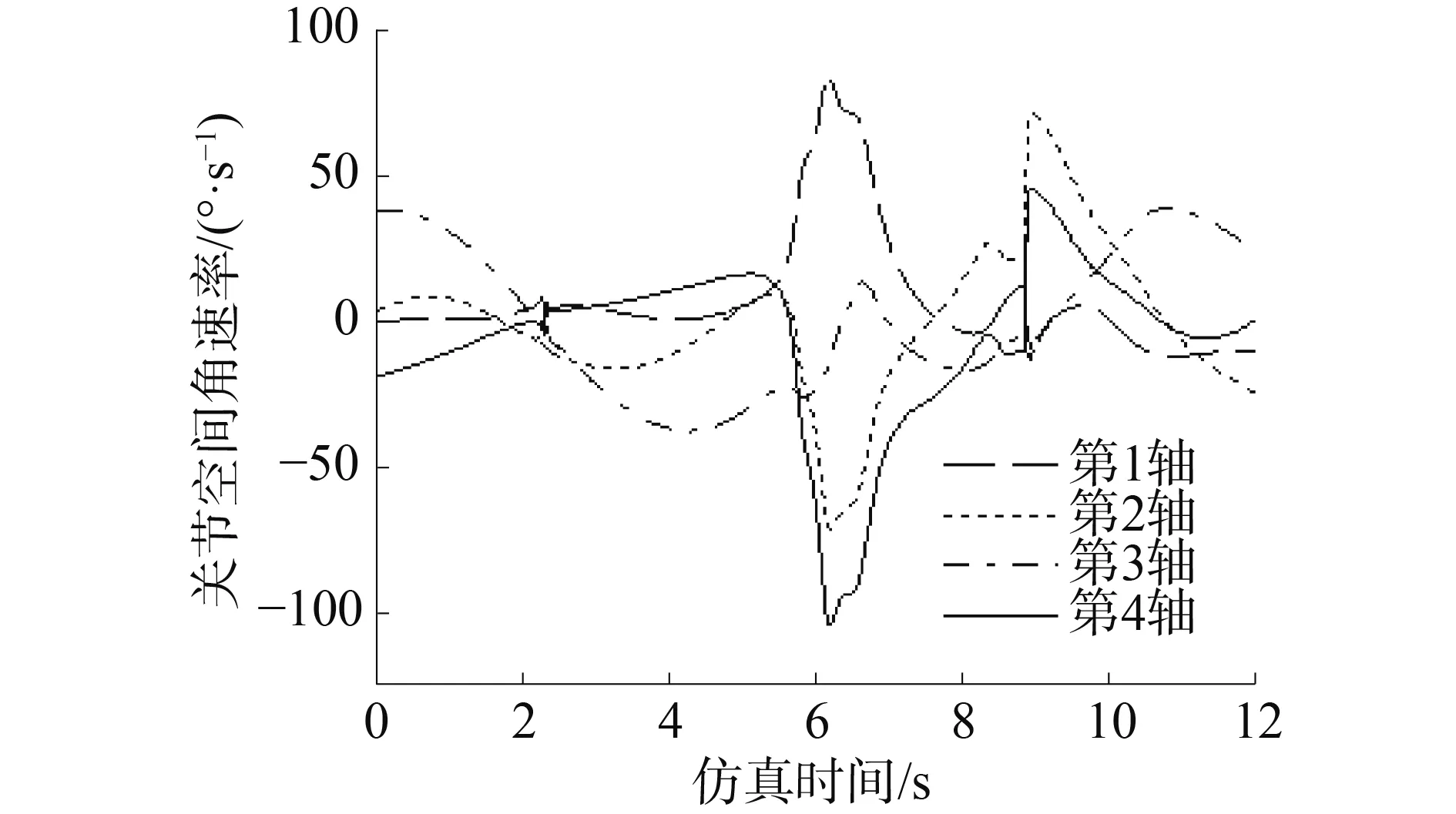
圖9 恒定速比方法中位置差分得到的速度值Fig.9 The velocity of joints obtained by positiondifference in RCC approach

從圖9誤差結果可以看出，利用恒定速比方法計算關節角位置，機構的末端姿態誤差不累加。雖然在某些位置出現誤差增加點，但整體末端姿態始終保持較高精度。同時，姿態精度取決于算法中牛頓迭代的精度，換而言之，根據末端姿態精度要求的不同，可以靈活選擇牛頓迭代法的精度。

5 結論

1)建立了具有4個運動自由度的天線穩定系統運動模型，給出了天線運動、運載器運動及目標衛星之間的關系；給出了天線姿態矩陣序列的計算方法。

2)分析了現有的冗余自由度運動學逆解方法在軌跡跟蹤方面的不足。提出了一種基于關節恒定速比的關節位置算法，給出了算法的流程圖。

3)對基于M-P逆的速度求解方法和本文提出的方法進行了仿真驗證，仿真結果表明恒定速比方法得到的關節角，保證了系統末端姿態在運動過程中具有足夠的精度。

[1] 吳鵬. 船用衛星天線姿態穩定系統關鍵技術研究[D].哈爾濱：哈爾濱工程大學, 2012： 17-23.

WU Peng. Key technologies of marine satellite antenna attitude stabilization system[D]. Harbin: Harbin Engineering University, 2012: 17-23.

[2] GUO Dongsheng, ZHANG Yunong. Acceleration-level inequality-based MAN scheme for obstacle avoidance of redundant robot manipulators[J]. IEEE transactions on industrial electronics, 2014, 61(12): 6903-6914.

[3] ZHANG Y, LI W, LIAO B,et al. Analysis and verification of repetitive motion planning and feedback control for omnidirectional mobile manipulator robotic systems[J]. Journal of intelligent & robotic systems, 2014,75 (3-4): 393-411.

[4] CAPISANI L M, FERRARA A. Trajectory planning and second-order sliding mode motion/interaction control for robot manipulators in unknown environments[J]. IEEE trans ind electron, 2012, 59(8): 3189-3198.

[5] XIAO L, ZHANG Y. A new performance index for the repetitive motion of mobile manipulators[J]. IEEE trans cybern, 2014,44(2)： 280-292.

[6] FLACCO F, DE LUCA A, KHATIB O. Control of redundant robots under hard joint constraints: saturation in the null space[J]. IEEE transactions on robotics, 2015, 31(3): 637-654.

[7] CHEN Dechao, ZHANG Yunong. A hybrid multi-objective scheme applied to redundant robot manipulators[J]. IEEE transactions on automation science and engineering, 2017，14(3)：1337-1350.

[8] FLACCO F, DE LUCA A. Optimal redundancy resolution with task scaling under hard bounds in the robot joint space[C]//Proc IEEE Int Conf Robot Seoul Korea, 2013: 3969-3975.

[9] ZHANG Dongsheng, XU Yundou , YAO Jiantao,et al. Kinematics, dynamics and stiffness analysis of a novel 3-DOF kinematically/actuation redundant planar parallel mechanism [J]. Mechanism and machine theory, 2017, 116:203-219.

[10] KUMAR A, KUMAR V. Evolving an interval type-2 fuzzy PID controller for the redundant robotic manipulator [J]. Expert systems with applications , 2017,73:161-177.

[11] KIM J, MARANI G, CHUNG W K, et al. A general singularity avoidance framework for robot manipulators: task reconstruction method[C]//IEEE International Conference on Robotics and Automation, New Orleas, 2004, 5: 4809-4814.

[12] MARANI G, KIM J, YUH J, et al. A real-time approach for singularity avoidance in resolved motion rate control of robotic manipulators[C]//IEEE International Conference on Robotics and Automation, Washington DC, 2002, 2: 1973-1978.

[13] ZORJAN M, HUGEL V. Generalized humanoid leg inverse kinematics to deal with singularities[C]∥IEEE International Conference on Robotics and Automation Karlsruhe Germany, 2013: 4791-4796.

[14] JAKUBIAK J, RATAJCZAK A. Kinematics and motion planning of the multi-bar system[J]. Journal of intelligent and robotic systems, 2014, 75(1): 5-15.

[15] RANDY C H, RODNEY G R, ANTHONY A M, et al. Designing a failure-tolerant workspace for kinematically redundant robots[J]. IEEE transactions on automation science and engineering, 2015, 12(4): 1421-1432.

[16] ZHANG Yunong, ZHANG Yinyan, CHEN Dechao, et al. From davidenko method to zhang dynamics for nonlinear equation systems solving[C]∥IEEE Transactions on Systems, Man, and Cybernetics: Systems. Budapest Hungary, 2016.

[17] LI S, LI Y. Nonlinearly activated neural network for solving timevarying complex Sylvester equation[J]. IEEE trans. cybern, 2014, 44(8): 1397-1407.

[18] ASFOUR T, DILLMANN R. Human-like motion of a humanoid robot arm based on a closed-form solution of the inverse kinematics problem[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas Nevada, 2003, 2: 1407-1412.

[19] 王英石.冗余機器人的運動學及軌跡規劃的研究[D].天津：南開大學, 2014.

WANG Yingshi. Research on the kinematics and trajectory planning of redundant robots[D].Tianjin: Nankai University, 2014.

[20] PEIPER D L. The kinematics of manipulators under computer control[R]. Stanford Univ Calif Dept of Computer Science, 1968: 32-66.

[21] LIEGEOIS A. Automatic supervisory control of the configuration and behavior of mutibody mechanisms[J]. IEEE trans sys man cyber,1977, SMC-7(12): 868-871.

[22] JIN Hongzhe, ZHANG Hui, LIU Zhangxing,et al. A synthetic algorithm for tracking a moving object in a multiple-dynamic obstacles environment based on kinematically planar redundant manipulators [J]. Mathematical problems in engineering, 2017(2): 1-15.

[23] DUBEY R V, EULER J A, BABCOCK S M. An efficient gradient projection optimization scheme for a seven-degree-of-freedom redundant robot with spherical wrist[C]∥IEEE international conference on robotics and automation, philadelphia, PA, USA, 1988: 28-36.

[24] WHITNEY D E. The mathematics of coordinated control of prosthetic arms and manipulators[J]. ASME journal of dynamic systems, measurement, and control, 1972, 94(4): 303-309.

[25] WAMPLER C W. Manipulator inverse kinematic solutions based on formulations and damped least-squares methods[J]. IEEE transactions on systems man and cybernetics, 1986, 16(1): 93-101.

[26] CHEN Yujen, JU Mingyi, HWANG Kaoshing. A Virtual torque-based approach to kinematic control of redundant manipulators[J]. IEEE Transactions on industrial electronics, 2017, 64(2): 1728-1736.

[27] BADLER N I, TOLANI D. Real-time inverse kinematics of the human arm[J]. Center for human modeling and simulation, 1996, 73: 392-401.

本文引用格式：吳鵬，洪娟，陳廣，等. 串聯冗余自由度機構關節角位置的規劃算法[J]. 哈爾濱工程大學學報， 2017， 38(10): 1623 -1629，1641.

WU Peng, HONG Juan, CHEN Guang, et al. Joints position planning approach for series redundant DOF mechanisms[J]. Journal of Harbin Engineering University， 2017， 38(10): 1623 -1629，1641.

JointanglepositionplanningapproachforseriesredundantDOFmechanisms

WU Peng1, HONG Juan2, CHEN Guang1, XU Bo1

(1.College of Automation, Harbin Engineering University, Harbin 150001, China; 2.Beijing Institute of Aerospace Control Device, Beijing 100854, China)

This paper proposes a method that can solve the joint angle position of a mechanism with series redundant DOFs in real time, solve the problem of attaining angular position in the inverse kinematics of the mechanism with series redundancy, and provide the numerical solution of inverse kinematics. According to weighted pseudo-inverse theory, this paper adopted the instantaneous optimum speed to represent the angle increment of joint space, studied the numerical solution of the joint space position, and presented the computing method for the joint space's angle position as the redundant DOF mechanism tracks the desired space attitude continuously. Under typical motion input conditions, the joint position and attitude errors obtained by constant speed ratio joint position algorithm and weighted inverse velocity integral method were simulated. To verify the effectiveness of the algorithm, the satellite antenna attitude stabilization system was taken as the research target. Simulation results show that the constant speed ratio joint position algorithm can ensure that the attitude error of the antenna Fresenius norm is less than 10-4in the process of inverse kinematic solution. Simulation results show that the proposed method can give the desired value of joint space position continuously in the movement process of a mechanism with redundant DOFs. The numerical solution of the position of the inverse kinematics can be realized, and control precision is ideal.

redundant manipulators; satellite antenna; weighted pseudo inverse; inverse kinematics; motion planning; constant rotation ratio (CRR); joint position; attitude stabilization; attitude error; Frobenius norm

10.11990/jheu.201607014

http://www.cnki.net/kcms/detail/23.1390.U.20170816.1550.042.html

TP241.3

A

1006-7043(2017)10-1623-08

2016-07-05. < class="emphasis_bold">網絡出版日期

日期：2016-08-16.

國家自然科學基金項目(61203225，61633008)；黑龍江省自然科學基金項目(QC2014C0669)；中央高校專項基金項目(HEUCF041702)；海洋工程國家重點實驗室開放課題項目(1616).

吳鵬(1978-)，男，講師，博士；徐博(1984-)，男，副教授，研究生.

徐博，E-mail:xubocarter@sina.com.