注射成型中聚合物剪切誘導(dǎo)結(jié)晶行為的三維模擬

趙朋，趙耀，嚴(yán)波，汪曉蔓，盧圣坤，傅建中

（1浙江大學(xué)機(jī)械工程學(xué)院，浙江省三維打印工藝與裝備重點(diǎn)實(shí)驗(yàn)室，浙江 杭州 310027；2上海交通大學(xué)材料科學(xué)與工程學(xué)院，上海 200030）

注射成型中聚合物剪切誘導(dǎo)結(jié)晶行為的三維模擬

趙朋1，趙耀1，嚴(yán)波2，汪曉蔓1，盧圣坤1，傅建中1

（1浙江大學(xué)機(jī)械工程學(xué)院，浙江省三維打印工藝與裝備重點(diǎn)實(shí)驗(yàn)室，浙江 杭州 310027；2上海交通大學(xué)材料科學(xué)與工程學(xué)院，上海 200030）

在考慮剪切導(dǎo)致分子鏈取向并升高其平衡熔點(diǎn)的基礎(chǔ)上，建立了基于 Nakamura方程的剪切誘導(dǎo)結(jié)晶動(dòng)力學(xué)模型。在WLF-Cross黏度模型中引入結(jié)晶對(duì)黏度系數(shù)的影響，構(gòu)建了考慮結(jié)晶的注射成型過程模型。采用改進(jìn)的有限體積法對(duì)聚合物剪切誘導(dǎo)結(jié)晶行為進(jìn)行了三維數(shù)值模擬，模擬中耦合了流動(dòng)場(chǎng)、熔體壓力、溫度、誘導(dǎo)時(shí)間與結(jié)晶度。結(jié)果表明，本方法可清晰模擬出注射成型過程中聚合物的三維“噴泉”流動(dòng)行為以及3層“皮-芯”結(jié)晶結(jié)構(gòu)，同時(shí)，誘導(dǎo)結(jié)晶時(shí)間指數(shù)與相對(duì)結(jié)晶度的模擬結(jié)果與理論及實(shí)驗(yàn)結(jié)果吻合。

注射成型；流動(dòng)；結(jié)晶；計(jì)算機(jī)模擬；有限體積法

引 言

在注射成型過程中，結(jié)晶型聚合物熔體被注射進(jìn)封閉的模具型腔中并經(jīng)冷卻固化成形，熔體在不同位置經(jīng)歷不同熱、力歷史，形成復(fù)雜的結(jié)晶形態(tài)，這種在加工過程中形成并最終凍結(jié)在制品中的結(jié)晶形態(tài)直接影響制品的使用性能[1-4]。然而，注射條件下聚合物結(jié)晶形態(tài)的控制理論還停留在粗略的定性階段[5]。研究聚合物在注射過程中的剪切誘導(dǎo)結(jié)晶行為，實(shí)現(xiàn)其結(jié)晶行為的“可視化”，及基于此的“定構(gòu)”調(diào)控，具有十分重要的科學(xué)意義和廣闊的應(yīng)用前景[6]。

近年來，國(guó)內(nèi)外學(xué)者圍繞聚合物的結(jié)晶形態(tài)、結(jié)晶動(dòng)力學(xué)及結(jié)晶過程模擬等領(lǐng)域開展了較多研究[7-10]。聚合物注射成型中結(jié)晶演化行為的模擬一般是基于修正的Nakamura方程進(jìn)行建模[11]，即以Nakamura方程為基礎(chǔ)，通過引入系數(shù)方程（如應(yīng)力[12]、應(yīng)變[13-14]、剪切速率[15-16]、溫度[17]等)來提高結(jié)晶動(dòng)力學(xué)模型的準(zhǔn)確性，如申長(zhǎng)雨等[18]基于Hele-Shaw假設(shè)，從熱力學(xué)能量角度對(duì) Nakamura方程的結(jié)晶速率常數(shù)進(jìn)行了修正。目前，注射成型中聚合物結(jié)晶過程的數(shù)值模擬還主要是結(jié)晶動(dòng)力學(xué)研究或基于 Hele-Shaw 薄壁流動(dòng)假設(shè)的表面流模擬[19]，注射條件下聚合物剪切誘導(dǎo)結(jié)晶行為的全三維模擬還很欠缺[20-21]。

有限體積法具有局部守恒和全局守恒的特點(diǎn)，能兼容有限元非結(jié)構(gòu)網(wǎng)格，同有限差分法一樣有利于處理對(duì)流項(xiàng)問題，廣泛用于流體計(jì)算領(lǐng)域[22-24]。然而，傳統(tǒng)有限體積法在求解擴(kuò)散問題中，當(dāng)擴(kuò)散系數(shù)在有限控制體界面兩側(cè)差異較大時(shí)，擴(kuò)散通量在界面附近會(huì)出現(xiàn)數(shù)值振蕩現(xiàn)象[25]。基于此，本文建立剪切誘導(dǎo)結(jié)晶動(dòng)力學(xué)模型，在黏度模型中引入結(jié)晶的影響，并采用改進(jìn)的有限體積法對(duì)注射成型中聚合物剪切誘導(dǎo)結(jié)晶行為進(jìn)行了三維數(shù)值模擬。

1 模型與算法

1.1 剪切誘導(dǎo)結(jié)晶模型

在注射成型工藝的熔體充模過程中，剪切應(yīng)變速率大，壓力場(chǎng)和溫度場(chǎng)分布復(fù)雜，是典型的非等溫非平衡流動(dòng)過程[26]，因此將非等溫過程看作無數(shù)微小時(shí)間段內(nèi)的等溫過程組成時(shí)，可得相對(duì)結(jié)晶度與誘導(dǎo)時(shí)間指數(shù)的微分方程分別為[21]

式中，uj為第j個(gè)速度分量，j=1,2,3，θ為相對(duì)結(jié)晶度；為誘導(dǎo)時(shí)間指數(shù)，即產(chǎn)生結(jié)晶行為的起始時(shí)間，ti為誘導(dǎo)時(shí)間，T為結(jié)晶溫度；下角標(biāo)“，”表示求偏導(dǎo)數(shù)；t為時(shí)間。ti與T關(guān)系見式（3）

式中，α為材料常數(shù)；Tm為平衡熔點(diǎn)；ti,T為溫度T時(shí)的結(jié)晶誘導(dǎo)時(shí)間；dt/ti,T為在溫度T時(shí)微小時(shí)間段對(duì)誘導(dǎo)結(jié)晶的貢獻(xiàn)，當(dāng)達(dá)到1時(shí)，誘導(dǎo)期結(jié)束，晶核形成并開始生長(zhǎng)。根據(jù) Nakamura方程，相對(duì)結(jié)晶度θ為時(shí)間t的函數(shù)

式中，n為 Avrami指數(shù)；t1/2為半結(jié)晶時(shí)間。結(jié)晶速率與溫度之間的關(guān)系如式（7）所示

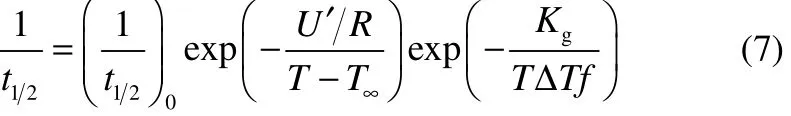
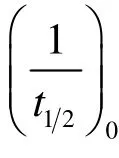
在剪切作用下聚合物熔體分子鏈被拉伸，減少了熔體構(gòu)象的種類，降低了熔體的熵，因此提高了平衡熔點(diǎn)溫度和過冷度。當(dāng)剪切應(yīng)力較小時(shí)，不足以拉伸熔體分子鏈以改變分子取向，但是剪切應(yīng)力過大，聚合物分子已經(jīng)得到足夠拉伸，繼續(xù)增加剪切應(yīng)力不再改變分子取向[27]，剪切應(yīng)力τ與等效熔點(diǎn)Tm之間的關(guān)系式為

式中，為零剪切應(yīng)力時(shí)的平衡熔點(diǎn)；C1、C2為材料參數(shù)。

1.2 注射成型過程建模

假設(shè)聚合物熔體為不可壓縮流體，慣性力和質(zhì)量力忽略不計(jì)，則由Navier-Stokes方程可簡(jiǎn)化得到聚合物熔體流動(dòng)的質(zhì)量守恒、動(dòng)量守恒以及能量守恒方程為[23]

式中，“，”表示求偏導(dǎo)；ui、p、T分別為第i個(gè)速度分量、壓力和溫度；η、ρ、cV、λ分別為熔體的動(dòng)力學(xué)黏度、密度、比熱容、傳熱系數(shù)；i, j= 1,2, 3為空間坐標(biāo)分量；為剪切應(yīng)變速率；δij為 Kronecker函數(shù)；φ為黏度剪切耗散功；為單位時(shí)間內(nèi)由于結(jié)晶釋放的熱量；Hc為單位質(zhì)量結(jié)晶的潛熱；˙為相對(duì)結(jié)晶速率。在充模階段，聚合物黏度模型采用7參數(shù)WLF-Cross模型，并且采用Titomanlio等[28]提出的經(jīng)驗(yàn)?zāi)Ｐ停陴ざ饶Ｐ椭幸虢Y(jié)晶對(duì)黏度系數(shù)的影響

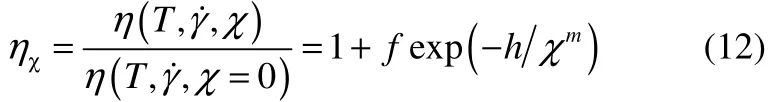
式中，ηχ為黏度變化因子；η(T,γ˙,χ=0)為不考慮結(jié)晶時(shí)由 WLF-Cross模型得到的聚合物熔體黏度；f、h、m為材料參數(shù)。

可是林師父自己畫風(fēng)，卻要我們畫水！他說：“平遠(yuǎn)細(xì)皺，起起伏伏，這是畫匠們的畫法，你們要學(xué)水奔湍巨浪，隨石曲折，隨物賦形，畫出水的神氣。畫好了水，才畫得出風(fēng)，畫得出光。”

充模結(jié)束后，聚合物熔體流動(dòng)停止。熔體在冷卻固化過程中繼續(xù)結(jié)晶，冷卻過程中的能量守恒方程為式(11)，此時(shí)熔體速度為0。

1.3 修正的有限體積法計(jì)算模型

傳統(tǒng)的有限體積法求解擴(kuò)散問題中，變量在有限體積中心連線上采用線性插值，當(dāng)擴(kuò)散系數(shù)在有限體積界面兩側(cè)差異較大時(shí)，擴(kuò)散通量則在界面兩側(cè)附近出現(xiàn)虛假數(shù)值振蕩。聚合物熔體為廣義非牛頓流體，熔體黏度隨溫度、壓力和剪切速率而劇烈變化，具有很強(qiáng)的非線性[29]，為提高模擬充模過程中熔體流動(dòng)速度的精度和穩(wěn)定性，需改進(jìn)傳統(tǒng)的有限體積法擴(kuò)散項(xiàng)離散格式[23,25]：速度變量沿有限體積中心連線需采用分段線性分布。

如圖1所示，P0、Pk為相鄰有限體積的中心，設(shè)χk=ηP0/ηPk為界面兩側(cè)相鄰有限體積中心的黏度比。假設(shè)速度在各有限體積內(nèi)呈線性變化，根據(jù)界面兩側(cè)相鄰有限體積的流動(dòng)剪切應(yīng)力相等原則可得相鄰有限體積的界面中心的速度梯度和速度的計(jì)算式為[23]

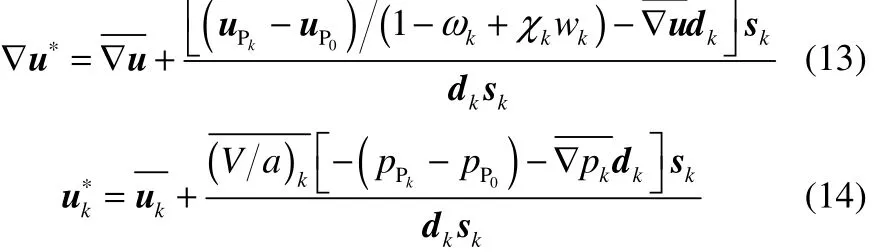
式中，u*為界面中心速度矢量；為有限體積中心位置矢量，Sk為P0有限體積界面的面積外法矢量，為加權(quán)系數(shù)，V為有限體積的體積，a為有限體積中心速度分量對(duì)應(yīng)方程組矩陣的主對(duì)角線上的值，分別為相鄰有限體積的值加權(quán)平均。

圖1 有限體積法單元Fig.1 Schematic diagram of finite volume

根據(jù)有限體積法建立每個(gè)有限體積上的離散的能量守恒方程

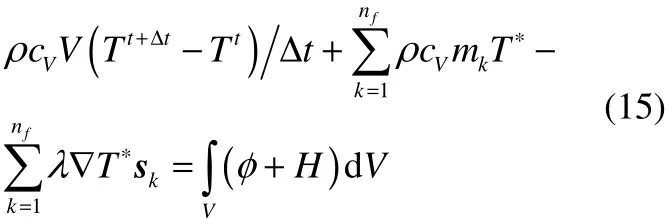
式中，Tt+Δt為 t+Δt時(shí)刻的溫度；Tt為 t時(shí)刻的溫度；Δt為時(shí)間步長(zhǎng)。為提高計(jì)算精度和穩(wěn)定性，對(duì)流項(xiàng)采用“延遲”算法。mk=u*sk為相鄰有限體積的界面上的流量。誘導(dǎo)時(shí)間指數(shù)與相對(duì)結(jié)晶度的有限體積法離散格式為

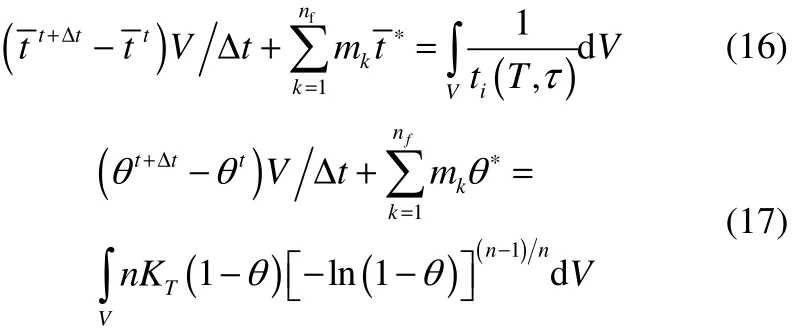
式中，為提高計(jì)算精度和穩(wěn)定性，對(duì)流項(xiàng)也采用“延遲”算法。

在充模過程中，在每個(gè)時(shí)間步長(zhǎng)內(nèi)，耦合求解速度和壓力方程直到速度、壓力和黏度的變化都很小：滿足設(shè)定的計(jì)算精度要求，然后求解能量方程，再求解誘導(dǎo)時(shí)間指數(shù)方程、相對(duì)結(jié)晶度方程。在冷卻過程中，假設(shè)熔體停止流動(dòng)，結(jié)晶繼續(xù)進(jìn)行，在每個(gè)時(shí)間步長(zhǎng)內(nèi)，順序求解能量方程、誘導(dǎo)時(shí)間指數(shù)方程、相對(duì)結(jié)晶度方程。注射成型過程中的結(jié)晶模擬流程如圖2所示。

2 結(jié)果與結(jié)論

2.1 算例分析

以ASTM-I型標(biāo)準(zhǔn)拉伸樣條為例，采用上述方法分析模擬注射條件下聚合物的剪切誘導(dǎo)結(jié)晶行為。拉伸樣條尺寸及其XYZ坐標(biāo)系位置如圖3所示，坐標(biāo)原點(diǎn)位于樣條的幾何中心。采用點(diǎn)澆口，澆口位于樣條端部側(cè)面的中心。聚合物材料選擇聚丙烯(PP)，其結(jié)晶物性參數(shù)如表1所示。

圖2 注射成型結(jié)晶過程模擬流程Fig.2 Flow chart of crystalline simulation during plastic injection molding

表1 聚合物PP的結(jié)晶參數(shù)Table 1 Crystallization parameters of polymers PP

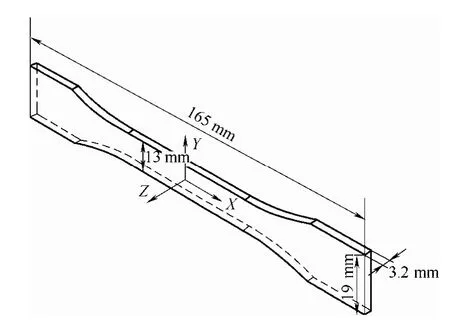
圖3 ASTM-I拉伸樣條及其坐標(biāo)系Fig.3 ASTM-I stretch bar and its coordinate system

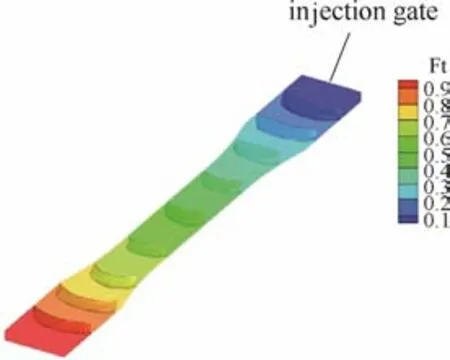
圖4 注射溫度240℃、模具溫度30℃、注射時(shí)間1 s時(shí)的熔體前沿流動(dòng)模擬Fig.4 Flow front results under process parameters of injection temperature 240℃, mold temperature 30℃ and injection time 1 s

注射溫度240℃，模具溫度30℃，注射時(shí)間1 s時(shí)的熔體前沿如圖4所示，色標(biāo)中Ft代表注射時(shí)刻。聚合物熔體由澆口（右上方端面中心）進(jìn)入型腔后，因型腔中心處的熔體溫度比靠近模具處的高，黏度更低，從而導(dǎo)致中心處的熔體前沿位置較腔壁處的熔體位置更突出，即“噴泉效應(yīng)”。由圖4可知，本文的方法可清晰地模擬出聚合物注射成型過程中的三維“噴泉”流動(dòng)行為。

不同時(shí)刻的誘導(dǎo)時(shí)間指數(shù)結(jié)果如圖5所示，注射溫度240℃，模具溫度30℃，注射時(shí)間1 s。色標(biāo)中I表示誘導(dǎo)時(shí)間，數(shù)據(jù)顯示為Z=0剖面上的結(jié)果。由圖可知，在10 s時(shí)整個(gè)型腔的誘導(dǎo)時(shí)間指數(shù)相對(duì)較低，只有靠近模壁的部分區(qū)域誘導(dǎo)時(shí)間指數(shù)相對(duì)較高。在20 s時(shí)模壁附近區(qū)域的誘導(dǎo)時(shí)間指數(shù)持續(xù)升高并達(dá)到1，但中心區(qū)域的誘導(dǎo)時(shí)間指數(shù)仍較低。這是因?yàn)槟＞邷囟容^低，在靠近模壁的位置剪切作用較強(qiáng)，所以在靠近模壁附近很容易產(chǎn)生較大的誘導(dǎo)時(shí)間指數(shù)。而型腔內(nèi)其他區(qū)域，雖然有剪切作用，結(jié)晶的等效熔點(diǎn)有所提高，但是熔體溫度較高，不易發(fā)生誘導(dǎo)形核。到30 s時(shí)，熔體溫度下降，整個(gè)型腔的誘導(dǎo)時(shí)間指數(shù)都達(dá)到了 1，即誘導(dǎo)期結(jié)束，晶核形成并開始生長(zhǎng)。圖6為模具溫度在20和40℃下冷卻到20 s時(shí)Z=0剖面上的誘導(dǎo)時(shí)間指數(shù)結(jié)果。如圖所示，隨著模具溫度升高，誘導(dǎo)時(shí)間指數(shù)達(dá)到1結(jié)束誘導(dǎo)期并開始形核結(jié)晶的時(shí)間越晚。這是因?yàn)槟卦礁撸垠w溫度下降速度越慢，從而導(dǎo)致達(dá)到結(jié)晶溫度范圍的時(shí)間越長(zhǎng)，結(jié)晶開始的時(shí)間也越晚。

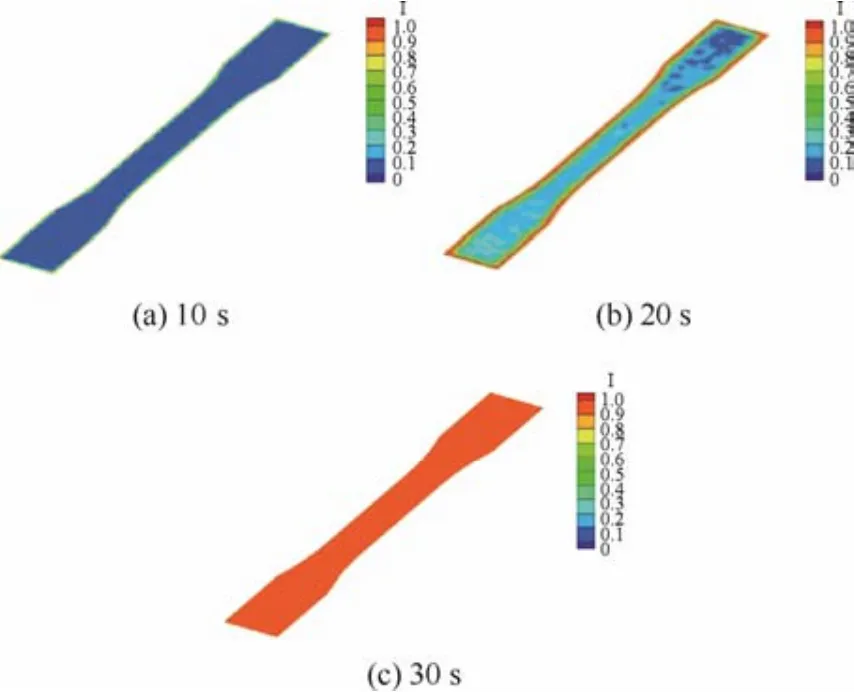
圖5 注射溫度240℃、模具溫度30℃、注射時(shí)間1 s下不同冷卻時(shí)刻的誘導(dǎo)時(shí)間指數(shù)結(jié)果Fig.5 Induction time index results at different cooling times under process parameters of injection temperature 240℃, mold temperature 30℃ and injection time 1 s

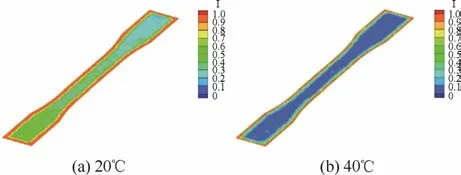
圖6 模具溫度為20℃和40℃、冷卻時(shí)間20 s的誘導(dǎo)時(shí)間指數(shù)結(jié)果Fig.6 Induction time index results at cooling time of 20 s under process parameters of mold temperature 20℃ and 40℃

不同時(shí)刻的相對(duì)結(jié)晶度結(jié)果如圖7所示，注射溫度240℃，模具溫度30℃，注射時(shí)間1 s。色標(biāo)中C代表相對(duì)結(jié)晶度，數(shù)據(jù)顯示為Z=0或X=0剖面上的結(jié)果。如圖所示，隨著冷卻時(shí)間的延長(zhǎng)，制品的相對(duì)結(jié)晶度不斷增大，同時(shí)，制品的相對(duì)結(jié)晶度分布呈現(xiàn)出復(fù)雜的3層“皮-芯”結(jié)構(gòu)。在模腔邊緣區(qū)域，因模具溫度低，聚合物熔體冷卻速度快，不易結(jié)晶，而在模腔中心區(qū)域，因聚合物傳熱系數(shù)較低，熔體溫度高也不易結(jié)晶，但在模腔邊緣與模腔中心之間，因剪切應(yīng)力較高且熔體溫度適中，其結(jié)晶度最高。

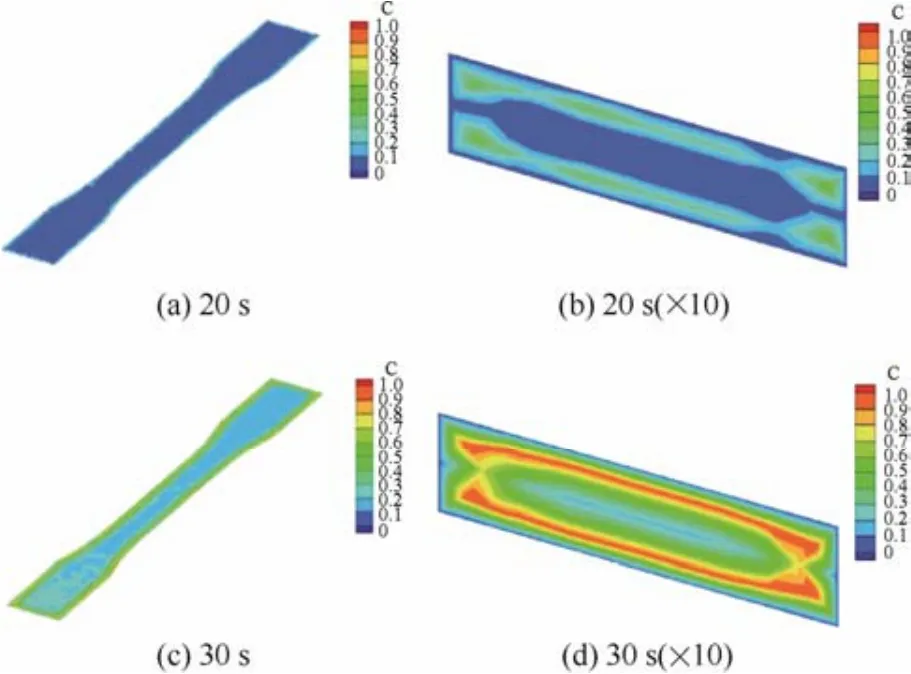
圖7 注射溫度240℃、模具溫度30℃、注射時(shí)間1 s下不同冷卻時(shí)刻相對(duì)結(jié)晶度結(jié)果Fig.7 Crystallinity results at different cooling times under process parameters of injection temperature 240℃, mold temperature 30℃ and injection time 1 s

下面將討論注射成型工藝參數(shù)（注射時(shí)間、模具溫度和熔體溫度）對(duì)聚合物結(jié)晶行為的影響。

注射時(shí)間分別為0.5和2.5 s下制品冷卻到30 s時(shí)Z=0剖面上的相對(duì)結(jié)晶度分布結(jié)果如圖8所示，其注射溫度為240℃，模具溫度為30℃。如圖所示，當(dāng)注射時(shí)間從0.5 s增大到2.5 s時(shí)，制品的結(jié)晶度出現(xiàn)上升趨勢(shì)。從剪切應(yīng)力角度看，短注射時(shí)間導(dǎo)致高剪切應(yīng)力，從而引起平衡熔點(diǎn)升高，誘導(dǎo)結(jié)晶更快進(jìn)行。從熔體溫度角度講，短注射時(shí)間引起熔體溫度升高，導(dǎo)致制品溫度高難以結(jié)晶且剪切應(yīng)力松弛更快。綜合兩方面影響因素，在本實(shí)驗(yàn)材料與注射條件下，注射時(shí)間的延長(zhǎng)可增加制品的相對(duì)結(jié)晶度分布，該結(jié)果與Guo等[27]的結(jié)論一致。

圖8 不同注射時(shí)間下冷卻30 s后的相對(duì)結(jié)晶度結(jié)果Fig.8 Crystallinity results at cooling time of 30 s under different injection times

模具溫度分別在20和40℃下冷卻30 s時(shí)制品X=0剖面上的相對(duì)結(jié)晶度分布結(jié)果如圖9所示，其注射溫度為240℃，注射時(shí)間為1 s。PP材料的結(jié)晶溫度范圍為20～120℃[30]。由圖可知，隨著模具溫度升高，制品“芯層”結(jié)晶度降低。這是因?yàn)槟＞邷囟雀邔?dǎo)致熔體熱量損失減少，從而引起制品中心熔體溫度高，結(jié)晶困難。同時(shí)，制品“皮層”的相對(duì)結(jié)晶度提高，且“皮層”與“芯層”之間的“中間層”向“皮層”移動(dòng)。隨著模具溫度的升高，使“皮層”附近的聚合物熔體冷卻速度下降，在 PP結(jié)晶溫度區(qū)間停留更長(zhǎng)時(shí)間，從而使該區(qū)域的相對(duì)結(jié)晶度升高。上述結(jié)論與文獻(xiàn)[30-31]的結(jié)論相吻合。

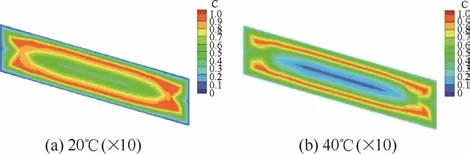
圖9 不同模具溫度下冷卻30 s后的相對(duì)結(jié)晶度結(jié)果Fig.9 Crystallinity results at cooling time of 30 s under different mold temperatures

注射溫度分別在220℃和260℃下冷卻30 s時(shí)X=0剖面上的相對(duì)結(jié)晶度分布結(jié)果如圖10所示，其模具溫度為30℃，注射時(shí)間為1 s。由圖可知，提高注射溫度可降低制品“芯層”的相對(duì)結(jié)晶度，其影響規(guī)律與提高模具溫度的影響類似，然而，因?yàn)槟＞邷囟染^低(30℃)，“皮層”的相對(duì)結(jié)晶度都很小。因此，可通過調(diào)整注射成型工藝參數(shù)可獲得具有不同結(jié)晶度分布的制品。

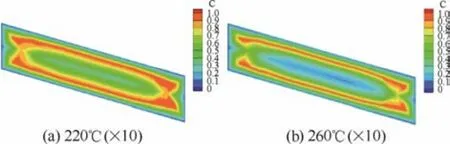
圖10 不同注射溫度下冷卻30 s后的相對(duì)結(jié)晶度結(jié)果Fig.10 Crystallinity results at cooling time of 30 s under different injection temperatures

2.2 實(shí)驗(yàn)驗(yàn)證

為進(jìn)一步驗(yàn)證本文所提方法的正確性，選取實(shí)際產(chǎn)品——非球面透鏡進(jìn)行實(shí)驗(yàn)驗(yàn)證，模具及產(chǎn)品CAD圖如圖11所示，透鏡中心厚5.2 mm。聚合物也選用PP，其結(jié)晶物性參數(shù)如表1所示。注塑機(jī)型號(hào)為HTL68/JD。注射溫度210℃，注射速度30%，模具溫度40℃，冷卻時(shí)間35 s，不設(shè)置保壓參數(shù)。

圖11 模具實(shí)物及產(chǎn)品CAD圖Fig.11 Aspheric lens mold photograph and lens CAD model

開模后，將透鏡置入液氮中淬火 3 min，以凍結(jié)其結(jié)晶結(jié)構(gòu)，然后采用差示掃描量熱儀(TA Q20 DSC)測(cè)量非球面透鏡“芯層”中心位置的結(jié)晶度，并將其與本文的模擬結(jié)果進(jìn)行對(duì)比分析。取 5～7 mg的試樣放入標(biāo)準(zhǔn)鋁盤并制樣，然后置入差示掃描量熱儀，以10℃·min-1的速率將試樣從40℃加熱至190℃，并記錄升溫過程中試樣的吸熱放熱曲線。根據(jù)曲線計(jì)算試樣的熔融熱焓ΔHf和冷結(jié)晶熱焓ΔHcc，試樣的絕對(duì)結(jié)晶度Xc可利用式(18)計(jì)算，為保證結(jié)果的準(zhǔn)確性和一致性，每種試樣重復(fù)測(cè)試3組。

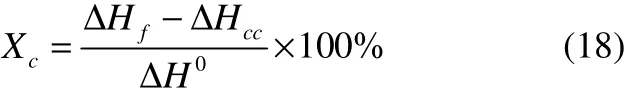
式中，ΔH0為100%結(jié)晶時(shí)(即完全結(jié)晶)每克的熔融熱焓，其值為207.0 J·g-1。

不同模具溫度下制品絕對(duì)結(jié)晶度的模擬結(jié)果與實(shí)驗(yàn)結(jié)果如圖12所示。DSC測(cè)量結(jié)果為絕對(duì)結(jié)晶度，而數(shù)值模擬結(jié)果為相對(duì)結(jié)晶度θt，如式（5）所示。為方便兩者比較，本文將模擬結(jié)果轉(zhuǎn)化為絕對(duì)結(jié)晶度χt，即χt=θt χ∞，其中χ∞=0.5。由圖可知，模擬結(jié)果與物理實(shí)驗(yàn)結(jié)果的結(jié)晶度變化趨勢(shì)相同，都是隨著模具溫度的增大，制品“芯層”中心的結(jié)晶度呈現(xiàn)減小的趨勢(shì)。如2.1節(jié)所述，模具溫度越高，熔體溫度下降速度越慢，從而導(dǎo)致達(dá)到結(jié)晶溫度范圍的時(shí)間越長(zhǎng)，結(jié)晶開始的時(shí)間越晚，同時(shí)，模溫高導(dǎo)致熔體熱量損失減少，從而引起熔體溫度高，制品結(jié)晶也更困難。但圖12中模擬結(jié)果與DSC結(jié)果存在一定誤差，主要是因?yàn)榻Y(jié)晶過程復(fù)雜多變，材料內(nèi)部包含結(jié)晶區(qū)域和無定形區(qū)域，本文數(shù)值模擬所采用的 Nakamura方程計(jì)算結(jié)晶度具有一定程度的近似[32]。此外，與密度不同，結(jié)晶度是相對(duì)概念，不同的結(jié)晶度表征方法，因?yàn)闇y(cè)量原理的不同，其結(jié)果也不一樣[33]。鑒于此，聚合物結(jié)晶度的數(shù)值模擬結(jié)果一般只與實(shí)驗(yàn)結(jié)果進(jìn)行演化趨勢(shì)對(duì)比[7-8,18]。

圖13是不同注射溫度下制品結(jié)晶度的對(duì)比，由圖可以看出，模擬結(jié)果與物理實(shí)驗(yàn)結(jié)果的結(jié)晶度變化趨勢(shì)也相同，都是隨著注射溫度的升高，制品“芯層”中心的結(jié)晶度呈現(xiàn)減小的趨勢(shì)。其影響機(jī)理與模具溫度的影響機(jī)理類似，注射溫度高，PP熔體將需要更多的時(shí)間冷卻至結(jié)晶溫度范圍，從而延緩了制品的結(jié)晶起始時(shí)間，同時(shí)，熔體溫度越高導(dǎo)致制品結(jié)晶越困難。

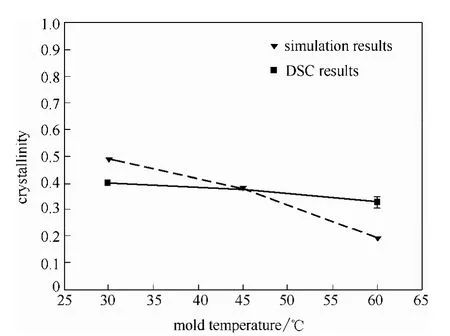
圖12 不同模具溫度下的絕對(duì)結(jié)晶度結(jié)果對(duì)比Fig.12 Results comparison of crystallinity under different mold temperatures

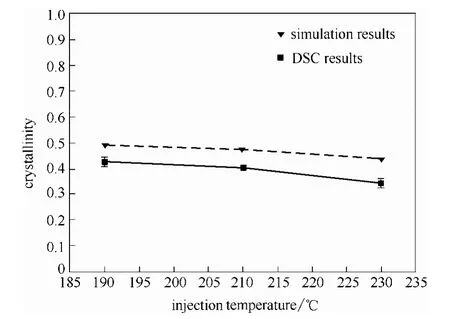
圖13 不同注射溫度下的絕對(duì)結(jié)晶度結(jié)果對(duì)比Fig.13 Results comparison of crystallinity under different injection temperatures

3 結(jié) 論

基于剪切誘導(dǎo)結(jié)晶模型、考慮結(jié)晶的注射成型過程建模和改進(jìn)的有限體積法，本文對(duì)注射成型過程中聚合物剪切誘導(dǎo)結(jié)晶行為進(jìn)行了三維數(shù)值模擬，研究了不同注射條件下聚合物誘導(dǎo)時(shí)間指數(shù)和相對(duì)結(jié)晶度分布的演化過程。數(shù)值結(jié)果表明，該方法可清晰模擬出注射成型過程中聚合物的三維“噴泉”流動(dòng)行為以及3層“皮-芯”結(jié)晶結(jié)構(gòu)，同時(shí)，誘導(dǎo)結(jié)晶時(shí)間指數(shù)與相對(duì)結(jié)晶度的模擬結(jié)果與理論結(jié)果吻合。模具溫度和注射溫度對(duì)制品最終結(jié)晶度分布影響較大，通過調(diào)整注射溫度與模具溫度可獲得所需要的結(jié)晶度分布。此外，以實(shí)際制品非球面透鏡為例，進(jìn)一步驗(yàn)證了本文所提出的方法的正確性，模擬結(jié)果與DSC測(cè)量結(jié)果的趨勢(shì)一致。

本文開發(fā)的結(jié)晶模擬軟件以及研究成果可用于分析注射成型過程中聚合物結(jié)晶形態(tài)的演變規(guī)律以及成型工藝對(duì)制品結(jié)構(gòu)與性能的影響機(jī)制，對(duì)聚合物結(jié)晶形態(tài)控制的實(shí)施和材料的高性能化研究具有重要意義，同時(shí)，在實(shí)際生產(chǎn)方面，可用于解決成型過程中的工藝分析、評(píng)價(jià)與優(yōu)化等問題，在聚合物制品性能的優(yōu)化控制方面具有廣闊的應(yīng)用前景。

[1] ZHAO P, PENG Y, YANG W,et al. Crystallization measurementsviaultrasonic velocity: study of poly(lactic acid) parts[J]. Journal of Polymer Science Part B: Polymer Physics, 2015, 53(10): 700-708.

[2] 嚴(yán)大東, 張興華. 聚合物結(jié)晶理論進(jìn)展[J]. 物理學(xué)報(bào), 2016, 65(18):101-111.YAN D D, ZHANG X H. Recent development on the theory of polymer crystallization[J]. Acta Physica Sinica, 2016, 65(18):101-111.

[3] TROISI E M, CARLERS H J M, PETERS G W M. Full characterization of multiphase, multimorphological kinetics in flow-induced crystallization of IPP at elevated pressure[J].Macromolecules, 2017, 50(10): 3868.

[4] SANTIS F D, VOLPE V, PANTANI R. Effect of molding conditions on crystallization kinetics and mechanical properties of poly(lactic acid)[J]. Polymer Engineering & Science, 2017, DOI:10.1002/pen.24414.

[5] 王柯, 張琴, 傅強(qiáng). 高分子加工制品的多層次結(jié)構(gòu)控制——從傳統(tǒng)加工到定構(gòu)加工[J]. 高分子學(xué)報(bào), 2013, (5): 583-588.WANG K, ZHANG Q, FU Q. Multi-level structure control of polymeric processed products—from traditional processing to structured machining[J]. Acta Polymerica Sinica, 2013, (5): 583-588.

[6] PANTANI R, COCCORULLO I, SPERANZA V,et al. Modeling of morphology evolution in the injection molding process of thermoplastic polymers[J]. Progress in Polymer Science, 2005,30(12): 1185-222.

[7] 阮春蕾, 劉春太. 剪切流場(chǎng)中聚乙烯結(jié)晶過程的建模與模擬[J].化工學(xué)報(bào), 2016, 67(5): 2144-2151.RUAN C L, LIU C T. Modeling and Simulation of polyethylene crystallization in shear flow field[J]. CIESC Journal, 2016, 67(5):2144-2151.

[8] 王錦燕, 陳靜波, 劉春太, 等. 聚合物流動(dòng)誘導(dǎo)結(jié)晶數(shù)值模擬[J].化工學(xué)報(bào), 2011, 62(4): 1150-1156.WANG J Y, CHEN J B, LIU C T,et al. Numerical simulation of polymer flow induced crystallization[J]. CIESC Journal, 2011, 62(4):1150-1156.

[9] 周應(yīng)國(guó), 申長(zhǎng)雨, 陳靜波. 半結(jié)晶性聚合物熔體冷卻過程雙尺度模擬[J]. 工程科學(xué)學(xué)報(bào), 2007, 29(2): 186-192.ZHOU Y G, SHEN C Y, CHEN J B. Two-scale simulation of melt-cooling process of semi-crystalline polymer[J]. Chinese Journal of Engineering, 2007, 29(2): 186-192.

[10] KOWALSKA B. Study on crystallization of polymers during the injection molding[J]. Polimery -Warsaw-, 2007, 52(2): 83-87.

[11] ZHOU H. Computer Modeling for Injection Molding: Simulation,Optimization, and Control[M]. Hoboken, New Jersey: John Wiley &Sons, 2013: 200-201.

[12] DOUFAS A K, MCHUGH A J. Simulation of melt spinning including flow-induced crystallization(Ⅲ): Quantitative comparisons with PET spinline data[J]. Journal of Non-Newtonian Fluid Mechanics, 2001,92(1): 81-103.

[13] TANNER R I. On the flow of crystallizing polymers(Ⅰ): Linear regime[J]. Journal of Non-Newtonian Fluid Mechanics, 2003,112(2/3): 251-268.

[14] JABBRAZADEH A, TANNER RI. Flow-induced crystallization:unravelling the effects of shear rate and strain[J]. Macromolecules,2010, 43(19): 8136-8142.

[15] TANNER R I. A suspension model for low shear rate polymer solidification[J]. Journal of Non-Newtonian Fluid Mechanics, 2002,102(2): 397-408.

[16] BOUTAOUS M, BOURGIN P, ZINET M. Thermally and flow induced crystallization of polymers at low shear rate[J]. Journal of Non-Newtonian Fluid Mechanics, 2010, 165(5/6): 227-237.

[17] ZINET M, OTMANI RE, BOUTAOUS M,et al. Numerical modeling of nonisothermal polymer crystallization kinetics: flow and thermal effects[J]. Polymer Engineering & Science, 2010,50(10): 2044-2059.

[18] 申長(zhǎng)雨, 周應(yīng)國(guó), 陳靜波. 半結(jié)晶聚合物注射成型中結(jié)晶動(dòng)力學(xué)的數(shù)值模擬[J]. 高分子學(xué)報(bào), 2008, (8): 771-777.SHEN C Y, ZHOU Y G, CHEN J B. Numerical simulation of crystallization kinetics during injection molding for semi-crystalline polymers[J]. Acta Polymerica Sinica, 2008, (8): 771-777.

[19] WANG X, KLAASEN B, DEGREVE J,et al. Volume-of-fluid simulations of bubble dynamics in a vertical Hele-Shaw cell[J].Physics of Fluids, 2016, 28(5): 243-258.

[20] 曹偉, 王蕊, 申長(zhǎng)雨. 塑料熔體在注塑模中的三維流動(dòng)模擬[J]. 化工學(xué)報(bào), 2004, 55(9): 1493-1498.CAO W, WANG R, SHEN C Y. Three dimensional flow simulation of plastic melt in injection mold[J]. Journal of Chemical Industry and Engineering(China), 2004, 55(9): 1493-1498.

[21] 嚴(yán)波, 李陽(yáng), 孔嘯, 等. 塑料注射成型結(jié)晶過程三維數(shù)值模擬[J].高分子學(xué)報(bào), 2011, (2): 173-179.YAN B, LI Y, KONG X,et al. Three dimensional numerical simulation of plastic injection molding process[J]. Acta Polymerica Sinica, 2011, (2): 173-179.

[22] DEMIRDZIC I, MUZAFERIJA S. Numerical method for coupled fluid flow, heat transfer and stress analysis using unstructured moving meshes with cells of arbitrary topology[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 125: 235-255.

[23] 嚴(yán)波, 李陽(yáng), 趙朋, 等. 基于改進(jìn)有限體積法的三維注塑成型充模過程數(shù)值模擬[J]. 機(jī)械工程學(xué)報(bào), 2015, 51(10): 25-32.YAN B, LI Y, ZHAO P,et al. Numerical simulation of mold filling process based on improved finite volume method[J]. Journal of Mechanical Engineering, 2015, 51(10): 25-32.

[24] 周文, 歐陽(yáng)潔, 楊斌鑫, 等. 三維非等溫非牛頓流體充模過程的建模與模擬[J]. 化工學(xué)報(bào), 2011, 62(3):618-627.ZHOU W, OUYANG J, YANG B X,et al. Modeling and simulation of 3D non-isothermal non-Newtonian fluid filling process[J]. CIESC Journal, 2011, 62(3): 618-627.

[25] 嚴(yán)波, 韓先洪, 孔嘯, 等. 改進(jìn)的有限體積法擴(kuò)散項(xiàng)離散格式[J].華中科技大學(xué)學(xué)報(bào)(自然科學(xué)版), 2012, 40(5): 20-23.YAN B, HAN X H, KONG X,et al. Improved finite volume method for diffusion term discretization[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(5):20-23.

[26] CHEN Y, ZOU H, LIANG M,et al. Melting and crystallization behavior of partially miscible high density polyethylene/ethylene vinyl acetate copolymer(HDPE/EVA) blends[J]. Thermochimica Acta,2014, 586(8): 1-8.

[27] GUO J, NARH K A. Simplified model of stress-induced crystallization kinetics of polymers[J]. Advances in Polymer Technology, 2002, 21(3): 214-222.

[28] TITOMANLIO G, SPERANZA V, BRUCAO V. On the simulation of thermoplastic injection process(Ⅱ): Relevance of interaction between flow and crystallization[J]. International Polymer Processing, 1997,12(1): 45-53.

[29] 李陽(yáng), 嚴(yán)波, 趙朋, 等. GLS/GGLS/SUPG 在三維注射成形充填模擬中的應(yīng)用[J]. 化工學(xué)報(bào), 2010, 61(2): 510-515.LI Y, YAN B, ZHAO P,et al.Application of GLS/GGLS/ SUPG in three dimensional injection molding filling simulation[J]. CIESC Journal, 2010, 61(2): 510-515.

[30] GUO J, NARH K A. Computer simulation of stress-induced crystallization in injection molded thermoplastics[J]. Polymer Engineering & Science, 2001, 41(11): 1996-2012.

[31] WANG L X, LI Q, SHEN C Y. The numerical simulation of the crystallization morphology evolution of semi-crystalline polymers in injection molding[J]. Polymer-Plastics Technology and Engineering,2010, 49(10): 1036-1048.

[32] GUO X, ISAVEV A I, DEMIRAY M. Crystallinity and microstructure in injection moldings of isotactic polypropylenes(Ⅱ): Simulation and experiment[J]. Polymer Engineering & Science, 1999, 39(11):2132-2149.

[33] LIMA M F S, VASCONCELLOS M A Z, SAMIOS D. Crystallinity changes in plastically deformed isotactic polypropylene evaluated by X-ray diffraction and differential scanning calorimetry methods[J].Journal of Polymer Science Part B: Polymer Physics, 2002, 40(9):896-903.

date:2017-05-04.

Prof. YAN Bo, chutian_yan@sina.com

supported by the National Natural Science Foundation of China (51475420, 51635006) and the Fundamental Research Funds for the Central Universities (2017QNA4003).

Three-dimensional simulation of shear-induced crystallization for polymers during injection molding process

ZHAO Peng1, ZHAO Yao1, YAN Bo2, WANG Xiaoman1, LU Shengkun1, FU Jianzhong1
(1Key Laboratory of3D Printing Process and Equipment of Zhejiang Province,College of Mechanical Engineering,Zhejiang University,Hangzhou310027,Zhejiang,China;2School of Materials Science and Engineering,Shanghai Jiao Tong University,Shanghai200030,China)

Based on shear induces polymer orientation and increases its equilibrium melting temperature, a Nakamura equation based shear-induced crystallization kinetics model was presented. A model for injection molding simulation was also established, in which the influence of crystallization was considered into WLF-Cross viscosity coefficient. Three-dimensional shear-induced crystallization behavior was simulated by an improved finite volume method, which coupled flow field, melt pressure, temperature, induction time index and crystallinity.Experimental results show that the proposed method can clearly simulate the three-dimensional “fountain” flow behavior and the three-layer “skin-core” crystallization structure during injection molding process. The simulated shear-induction time index results and crystallinity results agree well with the theoretical and experimental results.

injection molding; flow; crystallization; computer simulation; finite volume method

TQ 320

A

0438—1157（2017）11—4359—08

10.11949/j.issn.0438-1157.20170552

2017-05-04收到初稿，2017-07-20收到修改稿。

聯(lián)系人：嚴(yán)波。

趙朋（1983—），男，博士，副教授。

國(guó)家自然科學(xué)基金面上項(xiàng)目(51475420)；國(guó)家自然科學(xué)基金重點(diǎn)項(xiàng)目(51635006)；中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金資助項(xiàng)目（2017QNA4003）。