密閉容器內失控反應超壓的數學建模及其在壓力泄放中的應用

董澤，陳利平，陳網樺，馬瑩瑩

(1南京理工大學化工學院，江蘇 南京 210094；2索爾維投資有限公司（中國），上海 201108)

密閉容器內失控反應超壓的數學建模及其在壓力泄放中的應用

董澤1，陳利平1，陳網樺1，馬瑩瑩2

(1南京理工大學化工學院，江蘇 南京 210094；2索爾維投資有限公司（中國），上海 201108)

安全泄放是在失控條件下降低反應體系風險最為經濟有效的技術措施之一。研究壓力的數學模型既可以為泄放計算提供必要的參數，又可以讓工程師深入了解樣品在容器內的壓力變化情況，設計出更可靠的泄放系統，并且在減少實驗量的同時，還可以計算不同裝載率下的泄放面積。以20%DTBP（過氧化二叔丁基）的ARC（加速度量熱儀）測試為標準，結合理論推導得到了絕熱條件下密閉容器中失控反應超壓的數學模型，并將絕熱修正后的壓力測試曲線與模型模擬的壓力曲線對比，驗證了模型的正確性。最后，將模型的壓力模擬數據應用于20%DTBP的泄放計算中，結合Leung方法，得到了不同裝載率下的泄放面積，發現在裝載率為20%時，泄放面積達到最大為0.0035 m2。研究結果表明建立的壓力數學模型是正確可靠的，并且該模型能較好地應用于壓力泄放的計算中。

泄放計算；數學模型；加速度量熱儀；過氧化二叔丁基；模擬壓力

引 言

安全泄放是在失控條件下降低反應體系風險最為經濟有效的技術措施之一[1]。關于泄放方面的研究，20世紀70年代，美國緊急泄放系統設計協會[2-4]（DIERS）就對實際工廠中的化學超壓問題展開了研究，并取得了一系列的成果[5-7]。

Véchot等[8]利用了一個 0.1 L的容器研究了30%過氧化氫異丙苯在火災狀況下的泄放問題，發現其泄放過程中產生的壓力體系屬于調節混合體系，討論了不同泄放面積與反應釜體積比對于泄放過程的影響；Moncalvo等[9]以聚乙烯吡咯烷酮的水溶液為介質，研究了單相流泄放和兩相流泄放；Gustin[10]研究了苯酚和甲醛的反應在實際生產過程中發生冷卻失效時所需要的泄放面積。國內目前對這方面的研究還很少，對泄放口的設計大多基于國外早期的半經驗半理論公式，缺乏實驗依據。現有的一些研究，如 Jiang等[11]利用加速度量熱儀研究了過氧化二叔丁基的安全泄放問題，發現其熱分解時所產生的壓力體系為調節混合體系，并計算了其泄放面積；Deng等[12]利用Phi-TEC Ⅱ研究了過氧化二異丙苯的壓力泄放問題，發現其屬于混合體系；Jiang等[13]利用VSP2研究了醋酸乙烯聚合過程的壓力泄放問題，并計算了泄放所需面積。從國內外研究成果中可以發現，壓力泄放的研究都是以實驗為前提，即針對具體的反應做相應的實驗進行計算。有針對不同體系提出相應的計算方法，卻沒有嘗試過用模型模擬數據代替實驗進行計算。而泄放實驗往往需要的經濟成本和時間成本比較大，如果有適當的模型能代替實驗，既可以減少實驗量，又可以模擬一些危險性較大的反應情況。因此，對于化學超壓模型的研究是比較有意義的。

為了深入研究化學超壓模型，選擇 20%DTBP的甲苯溶液（簡稱 20%DTBP）為實驗對象（可調節混合體系[11]），一方面是 DTBP的分解動力學已被研究得到，可以直接用于泄放計算，并且甲苯是比較穩定的溶劑，不參與分解；另一方面，該樣品是一個混合體系，是壓力情況最復雜的一種體系，值得對其壓力組成進行研究。結合理論推導得到了絕熱條件下密閉容器中失控反應超壓的數學模型，并將絕熱修正后的壓力測試曲線與模型模擬的壓力曲線對比，驗證了模型的正確性。最后，將該模型模擬的壓力數據應用于泄放計算中，結合英國HSE泄放設計手冊中混合體系的泄放計算方法[14-16]，計算出了20%DTBP泄放時所需的面積。通過這個計算發現該模型不僅可以預測未知裝載率下的壓力情況，減少實驗量，還能為泄放計算提供必要的參數，計算出不同裝載率下的泄放面積，為設計更安全可靠的泄放系統提供幫助。

1 實驗測試與結果分析

1.1 試劑與測試條件

選用的測試樣品是20%DTBP溶液，是由過氧化二叔丁基與甲苯以質量比1:4混合制得，其常溫下密度為0.832 g·ml-1。其中甲苯作為溶劑既不參與反應也不參與分解。具體信息見表1。

測試所用加速度量熱儀[17]（accelerating rate calorimeter，ARC）是由英國THT公司開發生產，采用厚壁鈦球為測試球，實驗所用測試球的容積為10 ml（包括管道），溫度范圍 30～250℃。升溫程序為：30～90℃，10%功率線性升溫；90～250℃用加熱-等待-搜索模式測量樣品放熱情況，其中單個臺階的溫升為3℃，搜索的靈敏度為0.02 K·min-1。具體測試條件見表2。

表1 測試樣品的相關信息Table 1 Test sample information

表2 20%DTBP的ARC測試條件Table 2 ARC experimental conditions of 20%DTBP

1.2 結果與分析

從圖1和圖2中可以直接得到樣品的起始分解溫度、結束溫度、溫升等數據。從圖中發現，樣品的壓力變化趨勢與溫度變化趨勢較為接近，都是先緩慢升高再有一段爆發期。具體實驗結果見表3。

假設：

樣品中的DTBP完全分解，且純甲苯的密度表達式為[18]

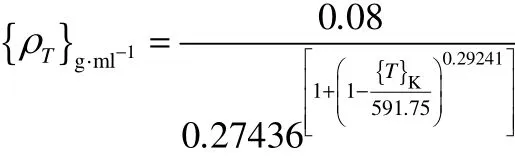
分別測定了20、40、60、80℃下混合樣品的密度為 0.832、0.818、0.799、0.778 g·ml-1，又計算了相應溫度下純甲苯的密度為0.841、0.823、0.805、0.786 g·ml-1，發現兩者密度與密度變化趨勢都很接近，又因為無法測量分解過程中的密度，且分解過程中樣品在高溫下會越來越接近純甲苯，因此用甲苯的密度表達式代替樣品分解過程中的密度是比較合適的。

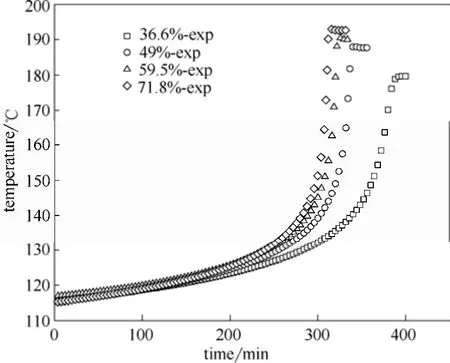
圖1 ARC溫度測試結果Fig.1 Temperature result in ARC

那么分解后容器內的空余體積（Vv,end）可以表示為容器總體積與樣品分解剩余體積的差

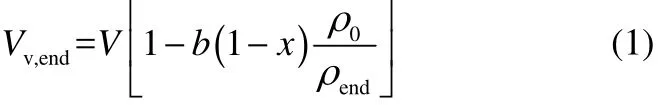
式中，b為裝載率；V為測試球總容積；x為樣品的質量分數，即20%；ρ0為裝樣時的樣品密度；ρend為分解完成時樣品的密度。求得分解完成時的空余體積結果，見表4。

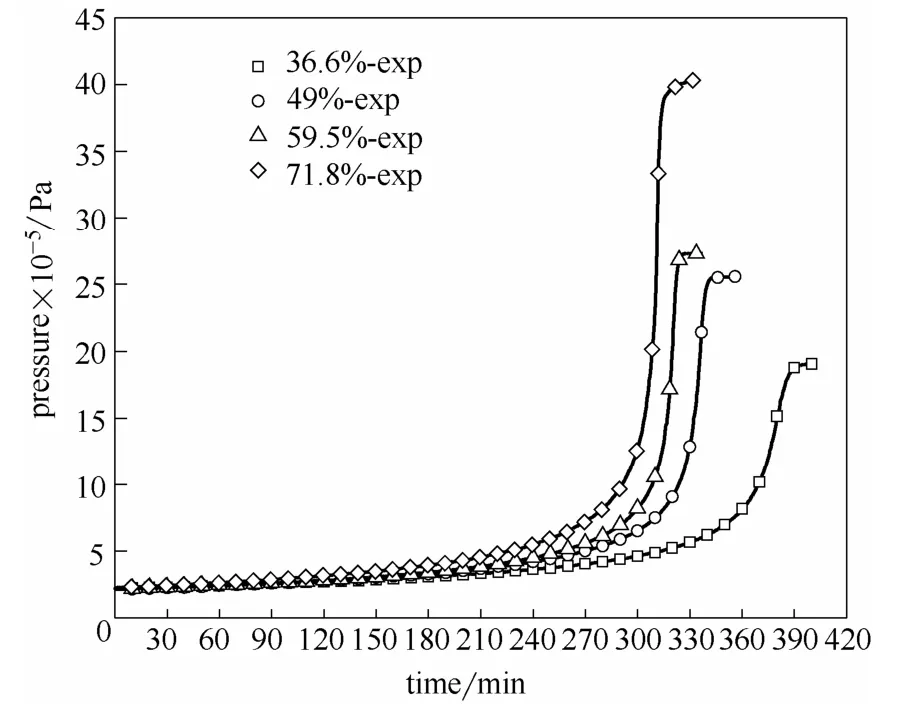
圖2 ARC壓力測試結果Fig.2 Pressure result in ARC

表3 20%DTBP的ARC測試結果Table 3 ARC experimental results of 20%DTBP

表4 20%DTBP的產氣量計算結果Table 4 Calculation result of gas generation of 20%DTBP

DTBP分解主要產物是丙酮和乙烷，還有少量異丁烯、叔丁醇和丁酮[19]，考慮到產物有可凝性氣體丙酮，用分解結束時的實際壓力來計算產氣量是比較合理的，即產氣量中包含了所有不可凝氣體和部分可凝氣體，是實驗數據換算得到的真實產氣量。根據4次測試得到了4種裝載率下樣品分解結束時的壓力（表4），該壓力值可以計算單位質量產氣量（v）。

分析分解完成時的壓力組成，包括3個部分：蒸氣壓（pV由未分解的溶液提供），背壓（pP由初始大氣壓力提供）和產生氣體的壓力（pG由DTBP分解提供），見式(2)

首先計算蒸氣壓pV。在ARC測試中，認為樣品分解前的壓力只與蒸氣壓和背壓有關，因此截取了測試中分解前的升溫段壓力數據，在經過背壓修正后用 Clapeyron方程對這部分蒸氣壓進行了非線性擬合，得到了蒸氣壓曲線方程，具體結果見圖3，用圖3中的蒸氣壓方程計算分解結束時的蒸氣壓，具體結果見表4。從表4的結果中發現，4種裝載率下的蒸氣壓都超過了總壓的10%，說明體系是一個可調節的混合體系[20]。

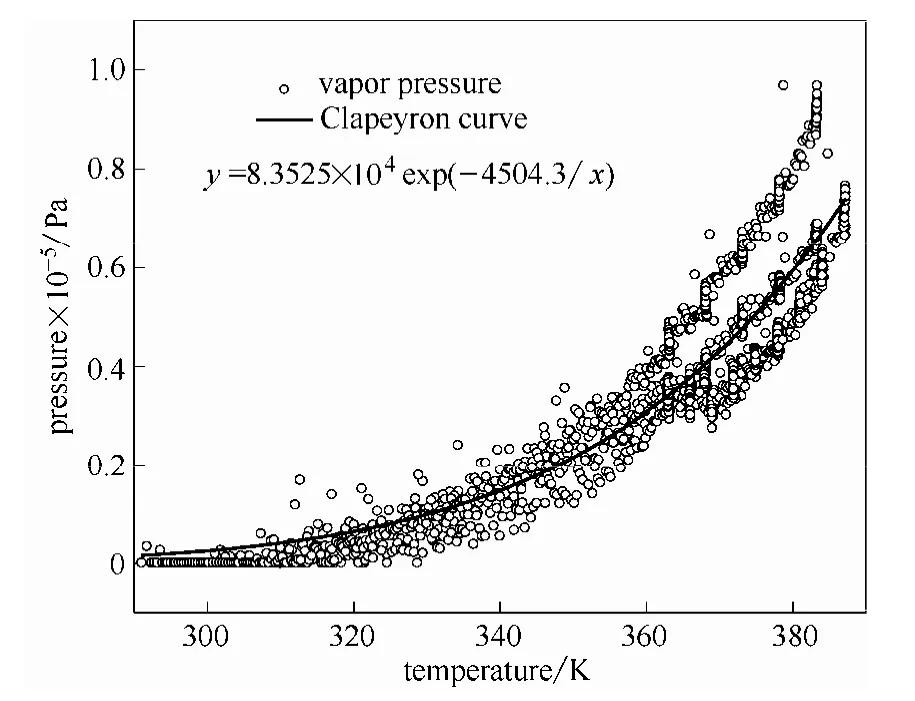
圖3 20%DTBP的蒸氣壓擬合曲線Fig.3 20%DTBP vapor pressure simulation curve

其次是背壓的計算。將產生背壓的氣體當作理想氣體，那么分解完成時的背壓即可表示為式(3)，計算結果見表4。

式中，初始背壓 p0為 1個大氣壓（1.013×105Pa）；初始溫度T0為20℃；V0為初始空余體積（表3）；Tend為分解結束溫度。

根據式(2)，產生氣體的壓力（pG）即為總壓與蒸氣壓和背壓的差。

將產生的氣體當作理想氣體處理即可計算出分解完成時產氣的物質的量，見式(4)

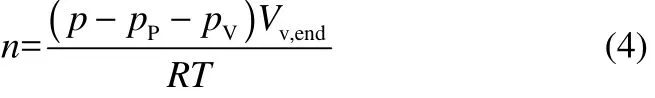
根據物質的量和測試的樣品量即可求算出單位質量的產氣量（v）

經計算求得4次測試的單位質量產氣量分別是0.000821、0.000715、0.000511 和 0.000474 mol·g-1。發現產氣量隨著裝載率增大而遞減，分析原因是由于 DTBP分解產生了部分可凝性氣體（丙酮），隨著樣品量增大，單位質量產生的丙酮是相同的，但由于溶劑量的增大，導致更多的丙酮溶解在了溶劑中，從而計算的產氣量在減小。根據產氣量和裝載率，在Origin中用不同數學模型進行擬合，發現二次函數模型的擬合結果相關系數最大為0.9435，因此選用該模型來擬合產氣量變化過程。具體模擬結果見圖4。

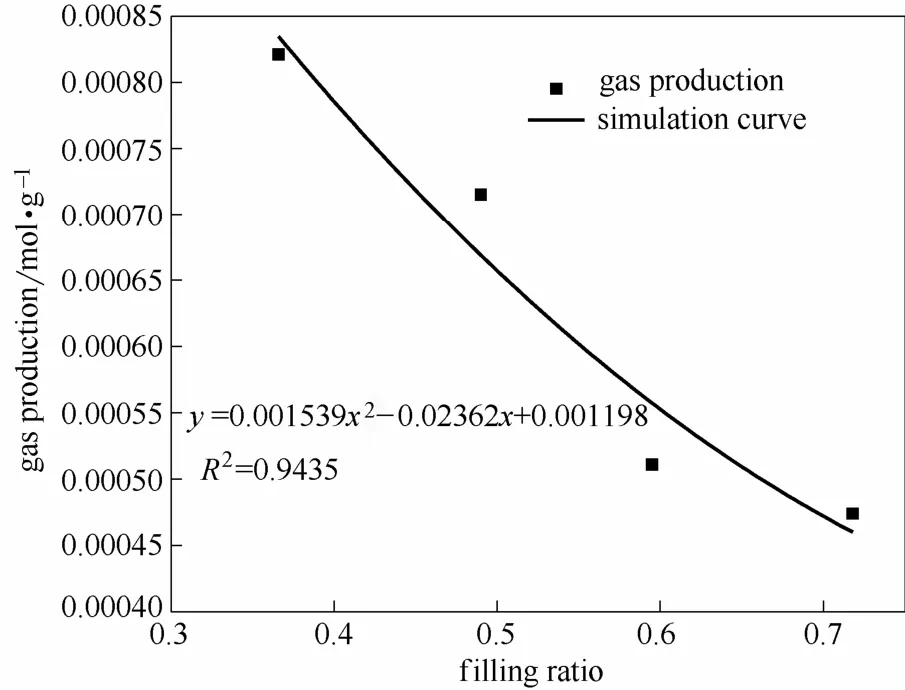
圖4 產氣量與裝載率關系曲線Fig.4 Simulation curve of gas production and filling ratio

2 數學模型與模擬結果

2.1 壓力隨轉化率與裝載率變化的數學模型

在工業生產中，反應釜內的壓力一般由背壓、產氣導致的壓力及蒸氣壓組成，背壓由溫度決定，蒸氣壓由物料組分比例及溫度決定，而產氣導致的壓力由樣品本身的性質決定，一方面可能是目標反應本身會產氣，另一方面可能是反應失控導致的物料分解產氣。工業上成熟的目標反應其壓力一般都是可控的，而相對不可控或者最危險的是失控反應，且往往導致非常嚴重的后果。因此，在設計壓力泄放系統時，需要按最危險情況來設計。

本文第 1節分析了壓力情況較為復雜的樣品（20%DTBP的甲苯溶液），將分析結果推廣到別的樣品中可以得到一個較為普適的壓力模型。該模型包含3個部分，背壓、產氣導致的壓力及蒸氣壓（有可能不涉及蒸氣壓，例如一些溶劑沸點特別高的樣品，或者不熔化直接分解的固體樣品等）。

在計算背壓和產氣導致的壓力時，空余體積的求算是最關鍵的一步，可表示為容器總容積與樣品所占體積的差，考慮到樣品分解與樣品密度隨溫度的變化都會導致樣品體積的變化，那么空余體積可以表示為

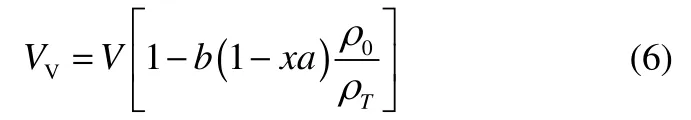
結合密度與溫度的關系式，且溫度（Tt）又等于起始分解溫度（Ton）與該時間下絕熱溫升（ΔTada）的和，以20%DTBP為例，那么空余體積可寫成

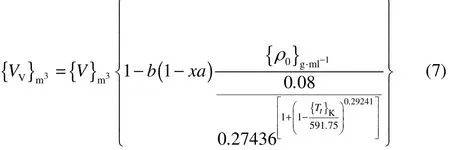
式中，b為裝載率；x為樣品質量分數；a為樣品轉化率；V為容器體積；R為氣體常數；ρ0為裝樣時的樣品密度；ρT為樣品密度函數。通過轉化率這個過程量，將溫度與空余體積聯系在一個公式中，充分描述了分解過程中空余體積的變化情況。

將產生背壓的氣體當作理想氣體，可以計算不同溫度下背壓的值，見式(8)

其中，初始背壓p0為 1個大氣壓（1.013×105Pa），初始溫度T0為20℃，V0為初始空余體積（表3），Tt為樣品任意時刻溫度。結合式(6)得到背壓的具體表達式

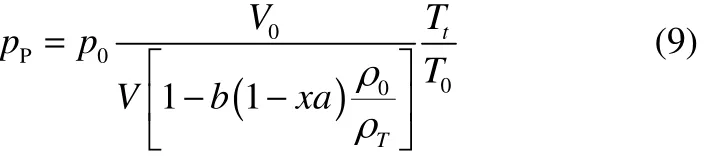
其次，根據單位質量產氣量v，可以計算出總產氣量ntotal（即為樣品質量與單位質量產氣量的乘積），見式(10)

其中單位質量產氣量對不同的樣品有不同的情況，若樣品分解只產生不可凝氣體，其值應為定值，若樣品分解有可凝性氣體，則其值會隨裝載率變化，求取方法可參考1.2節。

將產生的氣體當作理想氣體，結合轉化率（a）與理性氣體狀態方程，其壓力的表達式可寫成

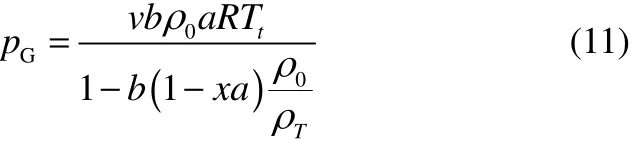
最后，根據1.2節中的蒸氣壓擬合方法，得到蒸氣壓方程，將其與產氣壓力、背壓相加即可得到分解過程中樣品壓力的變化方程，見式(12)

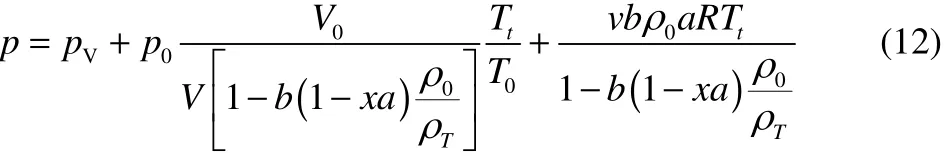
此模型中的溫度是模擬絕熱條件下的溫度，即樣品放熱完全用于加熱自身，phi值為1。

2.2 模擬測試結果的曲線

在上述數學模型中代入 ARC測試的相關參數（絕熱溫度Tt，裝載率b，密度函數ρT，單位產氣量v等），得到壓力與轉化率和裝載率的關系，結果見圖5。

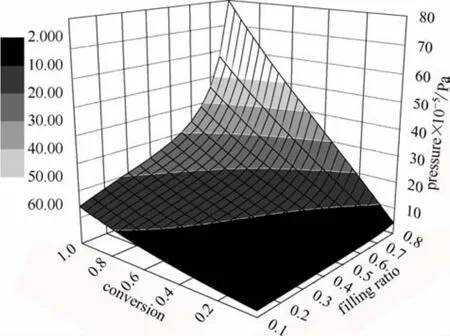
圖5 數學模型模擬得到的壓力隨轉化率與裝載率的變化Fig.5 Pressure vs conversion and filling ratio simulated by mathematic model

由于該模型模擬的是絕熱情況下的壓力變化（即phi值為1），在驗證結果的正確性時，需要將ARC數據進行絕熱修正，所用到的修正方法是Enhanced Fisher方法[21]，其修正結果見圖6，其中黑色實線為修正后的壓力與溫度曲線（從樣品分解開始到分解結束）。由于修正了被容器吸收的熱量，使得溫度比修正前更高，而更高的溫度反饋給樣品導致溫升也增大，且壓力是根據修正后的溫度來修正的，所以修正后的壓力也相應變大。

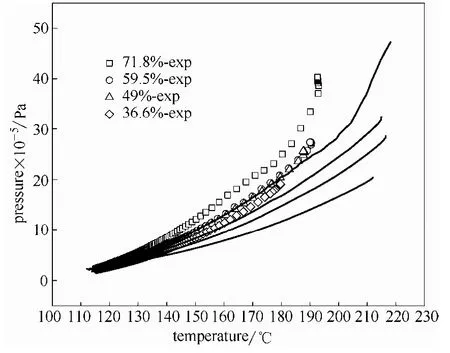
圖6 絕熱修正后的壓力曲線Fig.6 Pressure curves after adiabatic correction

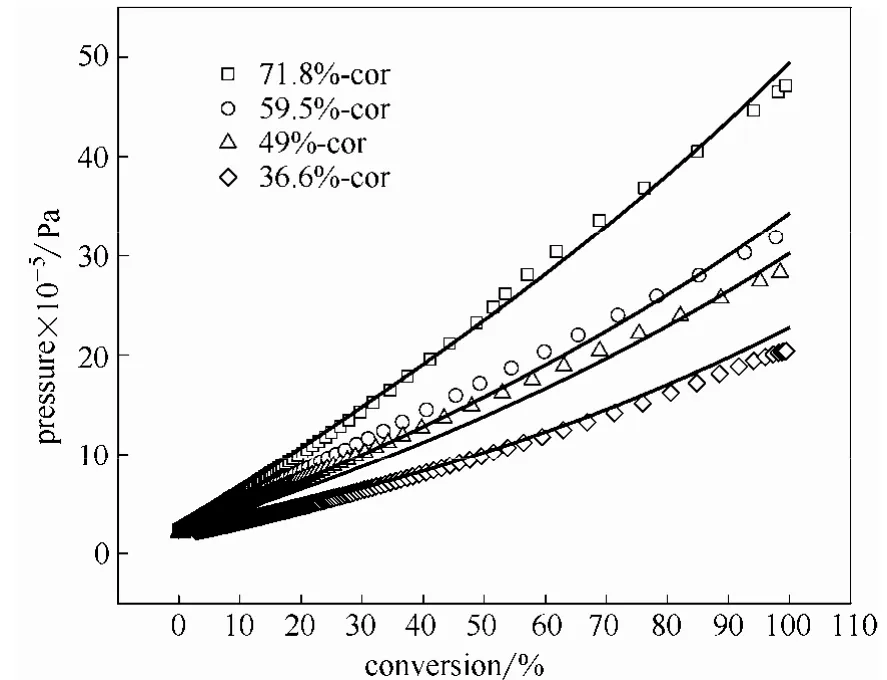
圖7 模型模擬結果與實驗絕熱修正結果的對比Fig.7 Pressure comparison between corrected and simulated curve

將修正結果中的溫度轉換成轉化率，與圖5中模擬結果對比得到圖7，發現兩者曲線幾乎重合。計算兩者的相關系數為0.9728，至此，該模型的正確性得到了驗證。

3 泄放面積的計算

化學反應失控所帶來的超壓危險是導致反應釜和儲罐爆炸的重要原因，運用緊急泄放技術對反應器或儲罐的泄放口進行設計，具有重要的應用價值。由于20%DTBP的超壓來源于甲苯的蒸氣壓和DTBP分解產生的小分子氣體，且甲苯蒸氣的泄放能帶走大量熱量，使反應釜內物料體系溫度保持恒定，因此確定反應過程中產生的壓力體系為可調節混合體系[11]。

根據第2節中的數學模型，任意裝載率和設定壓力下樣品的轉化率都可以得到。其中，轉化率可以計算出設定壓力下體系的溫度（當作絕熱計算），而溫度可以與反應動力學結合計算出設定壓力下的溫升速率，同理對于最大累積壓力下的相關參數也可如此得到。基于此，結合物質的特性參數，可以計算泄放所需的質量流量W。而單位面積質量流量G與物質本身性質、裝載率和反應釜相關，可以直接用Omega方法[22-24]計算得到。最終泄放面積就可以用公式A=W/G計算得到。

以20%DTBP為例，假設某工廠有容積為1 m3的 20%DTBP儲罐，其裝載率為 X，設定壓力為10×105Pa，在模型中找到對應的轉化率Y。在絕熱情況下，其對應的設定溫度 TR可表示為(115+101.5×Y)℃。同理設定最大累積壓力為12×105Pa，找到對應的轉化率為Xm，相應的最高允許累積溫度Tm表示為(115+101.5×Ym)℃，找到相應的轉化率Ym。根據文獻資料[25]，20%DTBP的分解動力學可以用方程描述為

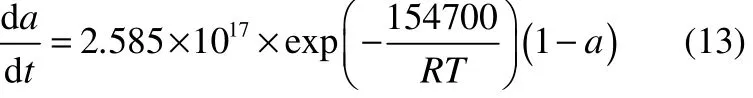
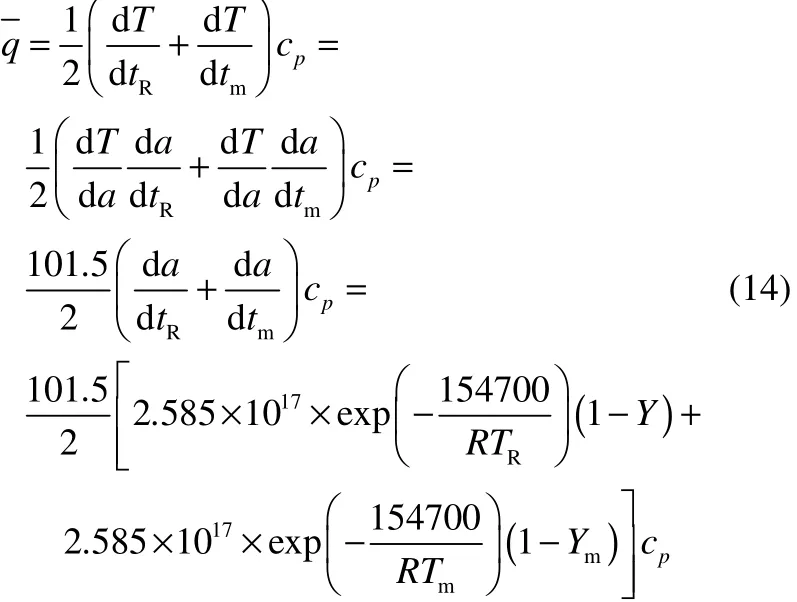
代入動力學方程即可得到平均放熱速率。由于20%DTBP是混合體系，W的計算公式如下

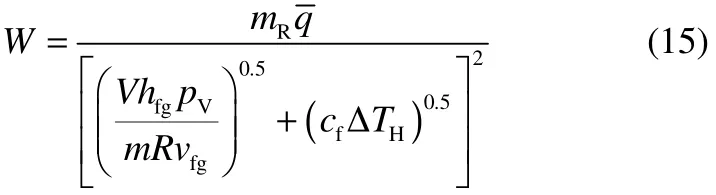
式中，mR為反應釜中物料質量，kg；為物料放熱速率，J·g-1；V為反應釜的容積，m3；hfg為物料的蒸發焓，J·g-1；vfg為蒸氣的比容，m3·kg-1；pV為設定壓力下的蒸氣壓，Pa；p為設定壓力，Pa；cf為物料的比熱容，J·g-1·K-1；ΔTH為設定壓力到最大允許壓力間的溫升，K。、hfg、vfg、cf均是設定壓力與最大允許壓力下的平均值。

根據Omega方法計算單位面積質量流量G，由于樣品屬于混合體系，需要同時對氣體部分和蒸氣部分進行G的計算。

第1步是Omega的確定：

氣體部分

蒸氣部分

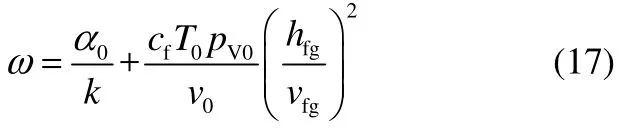
第2步是摩擦因子與背壓因子的修正，氣體與蒸氣的修正公式相同，如下

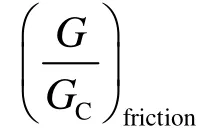
第3步是混合體系GR的確定

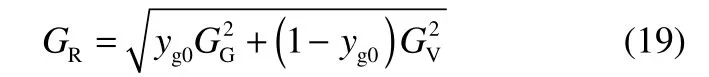
式中，yg0是氣體在氣相部分中的占比，GG與GV分別是氣體與蒸氣部分的G值。

最后一步是泄放面積的求取

基于對實際裝載量的參考，計算了10%～80%裝載率下的泄放面積與相關泄放參數。具體結果見圖8、圖9。

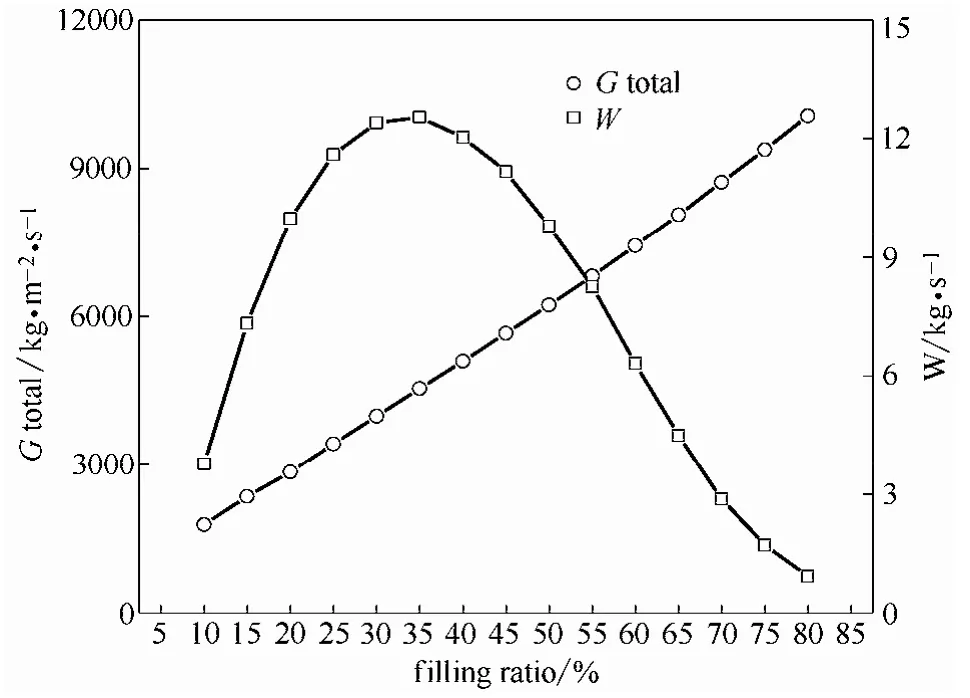
圖8 G與W隨裝載率的變化Fig.8 Curves of G and W vs filling ratio

從圖8、圖9中發現，20%DTBP所需的泄放面積與裝載率相關，質量流量W與泄放面積A都出現了先增后減的現象。從W的計算公式上分析原因，W的變化受到溫度和轉化率的雙重影響，溫度升高W變大，轉化率增大W變小，而溫度又是隨著轉化率變大而變大的，因此，在W的結果中會出現先增后減的趨勢。而泄放面積又與W正相關，因此也出現這種趨勢。根據計算結果，在1 m3的儲罐中，當設定壓力為10×105Pa時，20%DTBP泄放時所需的泄放面積在裝載率為 20%時達到最大，為 0.0035 m2。

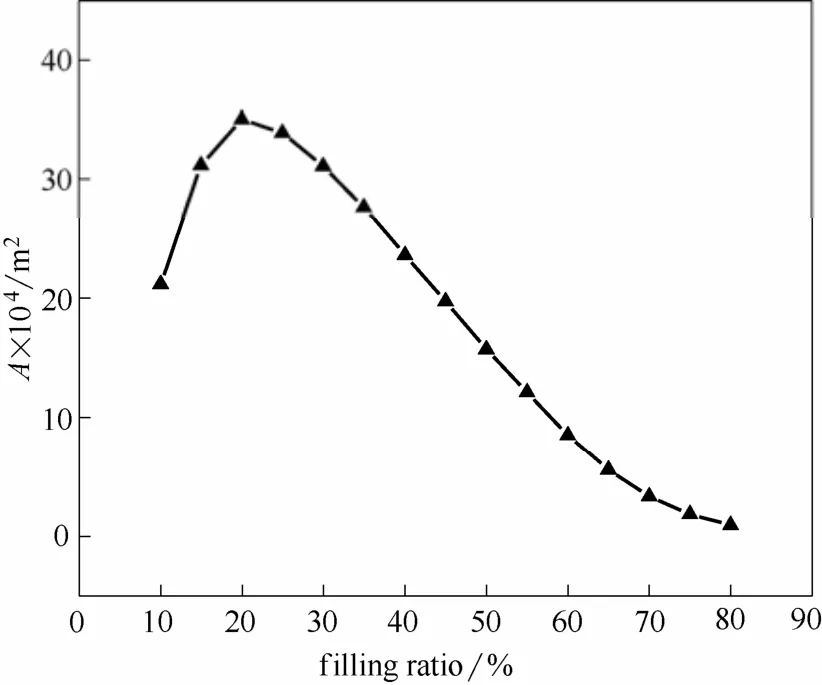
圖9 泄放面積A隨裝載率的變化Fig.9 Curve of relief area vs filling ratio

通過20%DTBP泄放計算的案例，發現壓力的數學模型可以為泄放計算提供必要的參數，在幫助計算泄放面積中起到較大的作用。

4 結 論

建立了絕熱情況下密閉容器中失控反應超壓的數學模型，模型方程如下

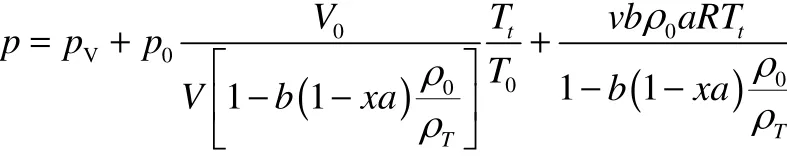
通過20%DTBP的ARC實驗驗證了數學模型的正確性，說明該模型適用于混合體系的壓力模擬，而混合體系是3種體系中壓力情況最復雜的一種，因此，理論上該模型也適用于另外兩種體系，即氣體體系和蒸氣體系。但實際該模型是否真的適用，還需要相關實驗的驗證。

通過分析20%DTBP的實驗結果，計算得到了該樣品蒸氣壓與單位質量產氣量的函數。

采用Leung方法，結合20%DTBP的壓力模擬圖，對20%DTBP的泄放進行了計算，求得1 m3儲罐中設定壓力為10×105Pa時泄放面積與裝載率的關系，并發現裝載率為20%時泄放面積達到最大為0.0035 m2。

該數學模型可以幫助計算任意裝載率下化學超壓泄放所需的面積，幫助設計安全可靠的泄放系統，為工廠的安全生產提供保障。

[1] 弗朗西斯·施特塞爾. 化工工藝的熱安全: 風險評估與工藝設計[M]. 陳網樺, 彭金華, 陳利平, 譯. 北京: 科學出版社, 2009:241-278.STOESSEL F. Thermal Safety of Chemical Process: Risk Assessment and Process Design [M]. CHEN W H, PENG J H, CHEN L P, trans.Beijing: Science Press, 2009: 241-278.

[2] FISHER H G, FOREST H S, GROSSEL S S,et al. Emergency Relief System Design Using DIERS Technology: The Design Institute For Emergency Relief Systems (DIERS) Project Manual [M]. New York:AIChE/DIERS, 1992: 285-393.

[3] FAUSKE H K. Emergency relief system design for reactive and non-reactive systems: extension of the DIERS methodology[J].Plant/Operations Progress, 1988, 7(3): 153-158.

[4] HUFF J E. Emergency venting requirements for gassy reactions from closed system tests[J]. Plant/Operations Progress, 1984, 3(1): 50-59.

[5] FISHER H G. An overview of emergency relief system design practice[J]. Plant/Operations Progress, 1991, 10(1): 1-12.

[6] 周建東. 化學反應失控緊急泄放研究[D]. 大連: 大連理工大學,2000.ZHOU J D. Emergency relief of runaway reaction [D]. Dalian: Dalian University of Technology, 2000.

[7] FAUSKE H K. Revisiting DIERS two-phase methodology for reactive systems twenty years later[J]. Process Safety Progress, 2006,25(3): 180-188.

[8] VéCHOT L, MINKO W, BIGOT J P,et al. Vent sizing: analysis of the blowdown of a hybrid non tempered system[J]. Journal of Hazardous Materials, 2011, 191(1): 8-18.

[9] MONCALVO D, FRIEDEL L. Single and two-phase flows of shear-thinning media in safety valves[J]. Journal of Hazardous Materials, 2009, 168(2): 1521-1526.

[10] GUSTIN J L. Vent sizing for the phenol + formaldehyde reaction[J].Organic Process Research & Development, 2006, 10(6): 1263-1274.

[11] WEI T T, JIANG H L. Venting design for di-tert-butyl peroxide runaway reaction based on accelerating rate calorimeter test[J].Chinese Journal of Chemical Engineering, 2012, 20(4): 710-714.

[12] DENG J P, SUN X, CHEN W H,et al. Thermal runaway risk and vent sizing of dicumyl peroxide[J]. China Safety Science Journal,2013, 23(9): 90-95.

[13] JIANG J, ZHANG C, CHAI X W,et al. Thermal runaway and safety relief of vinyl acetate polymerization reactors[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(5): 1119-1126.

[14] ETCHELLS J, WILDAY J. Workbook for Chemical Reactor Relief System Sizing [M]. Norwich, UK: HSE Books, 1998: 205-221.

[15] LEUNG J C. Venting of runaway reactions with gas generation[J].AIChE Journal, 1992, 38(5): 723-732.

[16] LEUNG J C, FAUSKE H K. Runaway system characterization and vent sizing based on DIERS methodology[J]. Plant/Operations Progress. 1987, 6(2): 77-83.

[17] TOWNSEND D I. Accelerating rate calorimetry [C]//I. Chem. E.Symposium Series, 1981, (68): 3.

[18] KAZAKOV A, MUZNY C D, CHIRICO R D,et al. Web Thermo Tables — an on-line version of the TRC Thermodynamic Tables[J].Journal of Research of the National Institute of Standards and Technology 2008, 113(4): 209.

[19] 周鴻娟, 劉敬蘭. 二叔丁基過氧化物分解產物的氣相色譜法測定[J]. 色譜, 1997, 15(4): 354-355.ZHOU H J, LIU J L. GC measurement for decomposition products of DTBP[J]. Chromatography, 1997, 15(4): 354-355.

[20] SINGH J. Vent sizing for gas-generating runaway reactions[J].Journal of Loss Prevention in the Process Industries, 1994, 7(6):481-491.

[21] KOSSOY A A, JASBIR S, ELENA Y K. Mathematical methods for application of experimental adiabatic data -an update and extension[J].Journal of Loss Prevention in the Process Industries, 2015, 33:88-100.

[22] LEUNG J C. A generalized correlation for one‐component homogeneous equilibrium flashing choked flow[J]. AIChE Journal,1986, 32(10): 1743-1746.

[23] LEUNG J C. The omega method for discharge rate evolution [R].New York: American Institute of Chemical Engineers, 1995.

[24] WOODWARD J L. An amended method for calculating omega for a homogeneous equilibrium model of predicting discharge rates[J].Journal of Loss Prevention in the Process Industries, 1995, 8(5):253-259.

[25] IIZUKA Y, SURIANARAYANAN M. Comprehensive kinetic model for adiabatic decomposition of di-tert-butyl peroxide using BatchCAD[J]. Industrial and Engineering Chemistry Research, 2003,42(13): 2987-2995.

date:2017-04-14.

Prof. CHEN Wanghua, chenwh_nust@sina.com

Mathematical model of runaway reaction pressure in closed container and its application in vent calculation

DONG Ze1, CHEN Liping1, CHEN Wanghua1, MA Yingying2
(1School of Chemical Engineering,Nanjing University of Science & Technology,Nanjing210094,Jiangsu,China;2Solvay(China)Co.,Ltd.,Shanghai201108,China)

Venting system that can reduce risks under runaway reactions was one of the most economical and effective measures. The study of pressure mathematical model provided necessary parameters for vent calculation,and helped engineers design more reliable venting system by understanding pressure tendency. Moreover, this model supported to calculate vent area in different filling ratios with less experiment. The ARC (accelerating rate calorimeter) test of 20%DTBP (di-tert-butyl peroxide) was chosen as the standard test. Combined with theory, the mathematical model of pressure in closed container was first deduced, which was suitable for adiabatic condition.Then, according to the comparison between adiabatic corrected test data and model simulated data, the correctness for this model was verified. Combined with Leung method, vent calculation was carried out with the model pressure simulation data. From the calculation, the vent area reached its maximum, while the filling ratio equaled 20%. The established closed container pressure model was correct and reliable. Furthermore, this model can be applied to the calculation of vent area.

vent calculation; mathematical model; accelerating rate calorimeter; di-tert-butyl peroxide; pressure simulation

X 933

A

0438—1157（2017）11—4453—08

10.11949/j.issn.0438-1157.20170403

2017-04-14收到初稿，2017-07-07收到修改稿。

聯系人：陳網樺。

董澤（1991—），男，博士研究生。