優化直觀引領 提增思維活力

江蘇建湖縣實驗小學 瞿德軍

優化直觀引領 提增思維活力

江蘇建湖縣實驗小學 瞿德軍

幾何直觀是借助圖形、符號等方式把復雜的數量關系變得簡明、形象、具體，促進認知的感性積累，加速認知表象的儲備，進而誘發思維的深入，有助于錯綜復雜關系的解剖。巧妙地利用線段圖、矩形圖等幾何直觀圖例，能夠幫助學生進一步理解、明晰數量之間的聯系，促進知識的提煉，促進數學思維的發展，從而使學生的數學學習充滿活力，洋溢著個性的色彩。

幾何直觀 數量關系 知識提煉 思維活力

“幾何直觀”是2011版《課程標準》中新增加的核心概念之一，“借助幾何直觀可以把復雜的數學問題變得簡單、形象，有助于探索解決問題的思路，預測結果。”憑借圖形的直觀性特點也能將抽象的數學語言變得簡潔清新，突破數學理解上的難點，使抽象思維水平不斷提升，幫助學生打開思維的大門，開啟智慧的鑰匙。幾何直觀就是一個極好的拐杖，讓學生在具體形象的情景中厘清數量關系、辨析內在聯系，突破數學問題的困擾，培養學生的解題技能，促進學生數學素養的發展。

一、巧作圖形明晰數量關系

數學問題中數量關系的復雜化不是個別現象，其有一定的歷史淵源，也有今天教育的功勞。新一輪的課程改革，力求我們的數學教學為學生的思維發展服務，著眼于思維的訓練，著力于能力的培養。然而，在實際的教學中原本很簡單的問題，在設計中非得安插一些多余的條件或者是不同的轉換說法，讓問題的層次豐富起來，讓各種數量之間的關系錯綜復雜起來，許多時候，學生根本就讀不懂問題說的是什么、講的是何物，教師被蒙的現象也時有發生。

靈活地引領學生做出直觀圖形，借助于見到的或想到的幾何圖形的形象關系，加速對題目當中較為隱晦的數量關系直接感知，從而貼近小學生形象思維為主的特性，促進學生的感悟。“數形結合”不僅是一種重要的數學思想，更是一種有效的學習方法，也是學習經驗的豐富與積累。它能有效實現代數問題與圖形之間的互相轉化，相互滲透，開拓解題思路，拓展學生的視角，提升思維的活力。

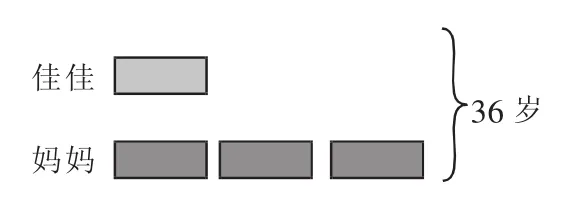
如，三年級“兩步計算的實際問題”教學中的習題：佳佳和媽媽的歲數一共是36歲，媽媽的歲數是佳佳的3倍，媽媽和佳佳各是幾歲？對于一個小學三年級的學生來講，該問題中數量關系的復雜性是不言而喻的，學生僅憑已有的認知水平和思維能力很難從正面進行突破。指導學生利用畫圖的方式，根據問題的倍量關系，將佳佳和媽媽的歲數分別用相同小長方形表示，借助圖形的線段圖的直觀作用，明晰數量、厘清關系，有效地突破解決問題的瓶頸。

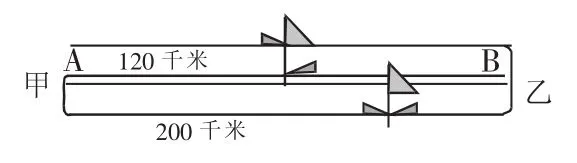
又如，這樣一道關于行程問題的習題：甲乙兩輛汽車同時從A、B兩個城市相對開出，第一次相遇在離A地120千米處。后繼續保持原速前行，到達對方城市后立即返回，結果在離A地200千米處再次相遇。計算出兩個城市之間的距離。初看習題，僅有孤零零的2個數據，讓人的頭腦都大了。如果我們引導學生仔細閱讀，引導學生學會用線段圖揭示其中的關系，把握每一輛汽車的運動軌跡，我們會有驚喜的發現。甲車和乙車的行駛時間相同，因為速度不同，所以行程也不同，但每種車每一個全程中行駛路程是永遠不變的，甲乙兩車（綠線和藍線的總和）一共行駛的是3個全程，就意味著甲車行駛了120×3=360千米，如再加上200千米，就意味著完成2個全程，所以兩個城市之間的距離是（360+200）÷2=280千米。

因此，針對現行的數學教學，利用適宜的圖形引導小學生積極地觀察、仔細地研究、準確地畫圖，從而促進數量關系清晰化，在辨析思考中號準問題的脈，排除無謂的干擾。借助圖形的直觀作用，引發聯想，喚醒認知，以具體的形象促進學生深入地思考，最終變抽象為直觀、化復雜為簡單，能有助于我們科學地辨析，快速地找到問題的答案和問題的實質。經過長期的訓練和運用，必定會有助于學生活動經驗的積累，更有助于學生思維水平的大幅度提升。

二、巧用直觀加速概念提煉

選擇直觀教學的目的就是讓學生在真實的視角中獲得更多的體驗，從而豐富感知，加速表象的積累，為知識的理解和運用提供厚實的基礎，刺激思維，使學習步入到一個高效的環節。同時，也促使學生的認知水平得到發展，形成扎實的技能。小學生的抽象思維還在逐步形成和成長之中，因此，他們無法科學地解讀數學概念，把握概念本質。為此，在具體的教學環節中借助實物操作或者具體的圖形、圖像，刺激學生的感官，以豐富的形象誘發抽象分析，發展抽象思維。

如，在五年級《分數的意義》教學中就可以充分運用幾何直觀，幫助學生理解和建構“1”的概念，并使之以具體的表象永久地存儲于學生的腦海中。

生：我用長方形表示所有的橘子，平均分成2份，其中的1份就是橘子的

……

師：現在和老師一起數一數是幾個橘子。你打算怎樣表示出這些橘子呢？

生：6個橘子畫成6個○。

生：可以畫成6個□。

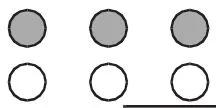
生：我是把6個再平均分成2份，涂的了。了。

師：有道理啊！那你框起來意味著什么呢？

生：就是把所有的橘子看成一個整體。

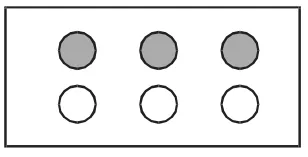
師：很好！向這樣的橘子我們可以理解為一個整體。想想我們的身邊還有哪些物品是可以理解為一個整體呢？

生：像1杯水。

生：像1堆沙子。

生：像一摞練習本。

……

生：也把6個橘子看成一個整體，平均分成3份，涂好其中1份就是。

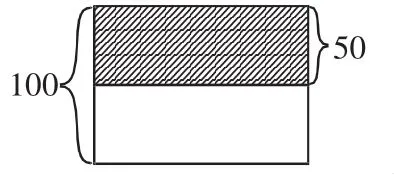
生：我用一個長方形表示100個

生：我這樣畫圖的。

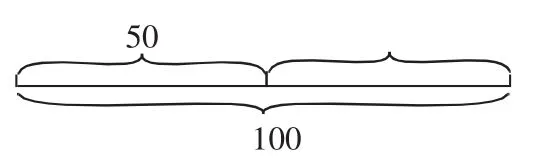
生：不一樣的。橘子有的是6個、8個、100個。

師：理解得很不錯。如果是一大堆的橘子，我們又該如何表示出它的呢？

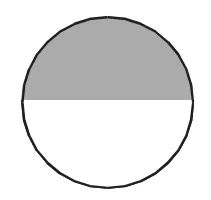
生：還是用長方形表示這堆橘子，平均分成2份，1份就是它的

生：也可以用一個圓圈表示全部的橘子，平均分成2份，1份是它的

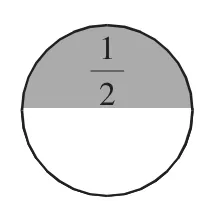
生：“1”。

師：這個1和1個橘子的1是一樣嗎？

生：不一樣。1個橘子的1是指具體的數量，而“1”表示的是一個整體。

師：很正確。你能說說“1”可以是什么嗎？

生：1個蘋果。

生：1箱蘋果。

生：1大堆蘋果。

師：你們的追述很有趣，這些蘋果都能用“1”表示，那說明“1”能代表什么呢？

……

案例中直觀幾何的運用，讓我們體會到它的魅力和價值，它不僅給學生具體的感知，讓學生獲得真實的體驗，也讓學生逐漸領悟一個整體的意義，并為正確建構“1”積累了豐富的感知，有利于新知的建模。

同時，利用幾何直觀促進了“1”認知的學習，起到了數形結合，情境交融的良好效果。執教者為了學生科學地建構，正確地理解“1”，多次安排學生動手畫一畫、圈一圈等活動，使學生明白“1”的模糊性和高度的概括性，它可以是1個蘋果、1箱蘋果、1堆蘋果……從而科學建模，進一步理解“1”的本質。學生嘗試畫圖，反饋交流，能夠科學地把握圖畫的本質，充分感知平均分與“1”之間的有機聯系。我想這樣的學習活動、體驗過程，學習的領悟一定是深刻的，學習的記憶一定是難以磨滅的。

三、善畫圖例加速學習感悟

小學數學中存在著許多條件之間、條件與問題之間的聯系不明顯的數學問題，而該時期的小學生思維能力不足以辨清它們的聯系，思維活動也會受挫、受阻，如不能適宜地點撥、指導，給予學生思維方法的引領，勢必會影響學生學習的熱情和探索的興趣，最終會影響教學的實效。

因此，加強直觀圖形的引入，引領學生正確繪制示意圖，有助于揭示隱藏數量，使關系明晰，促進深刻。引導學生學會畫圖，有效利用直觀圖形手段輔助教學，促進學生深入思考，激發學生合作探究的熱情。通過圖形的繪制和解析，很輕松地揭示隱藏在復雜關系背后的數量關系，促使學生明晰聯系，找準關系順利分析出解答思路，找準問題的突破口。既提高了學生畫圖能力和思維水平，還培養了學生創新意識。

指導學生靈活地繪制示意圖不僅能加速有效學習的進程，也有助于突出教學關鍵。在教學實踐中教師們都有這么一種深刻的體會思考研究解答一道題目，能否號準問題的脈、切透找準問題的關鍵，是我們教學的重點和關鍵所在。這要求我們關注小學生的思維水平，吃準他們空間想象能力的現狀，引導學生畫一畫，以圖促思，以圖促解，有效克服思維不縝密的局限讓直觀圖成為學生思維的翅膀，使學生能夠自由地徜徉在知識的海洋之中。

例如，在教學“長方形和正方形的周長”時，設計這樣的練習：（1）把2個邊長為2厘米的正方形拼成一個長方形，拼成的長方形周長是多少厘米？（2）把3個邊長為2厘米的正方形拼成一個長方形，拼成的長方形周長是多少厘米？（3）把4個邊長為厘米的正方形拼成一個長方形，拼成的長方形周長是多少厘米？從中你有什么新的發現？（4）把10個邊長為2厘米的正方形排成一列，拼成一個長方形，拼成的長方形周長是多少厘米？（5）把100個邊長為2厘米的正方形排成一列，拼成一個長方形拼成的長方形周長是多少厘米？利用一組問題的研究，啟迪學生深入思考，從畫圖解答中領悟排成一列的內在規律，探尋出解決問題的科學方法，讓學生在情緒高漲、興趣濃厚的情形下掌握思想方法。

由此可見，幾何直觀靈活運用能夠很好地引發學生學習數學的興趣，促進學生對學習的關注，

有助于學生積極地思考，有利于學生的素養發展。因而，我們在實際教學中要靈活運用，讓數學不再枯燥、不再抽象晦澀，滲透“數形結合”思想，讓我們的數學教學之路越來越平坦。當然，我們也應清醒地認識到，幾何直觀的培養不是一蹴而就的，而應貫穿整個小學數學學習的全過程，通過對學生幾何直觀能力的培養，使學生學會數學的一種思考方式和學習方式，以促進學生能力的提升和數學素養的發展，并為其終身學習奠定厚實的基礎。