巧用數形結合,讓計算教學更深刻些
江蘇溧陽市泓口小學 莊麗娟
巧用數形結合,讓計算教學更深刻些
江蘇溧陽市泓口小學 莊麗娟
在計算教學中,數形結合思想是一種可使復雜問題簡單化、抽象問題具體化的數學思想方法。要想提高學生運用數形結合思想的能力,需要教師耐心細致地向學生滲透這一思想。數形結合,可以讓計算情境更深度,讓算法探究更深化,讓計算練習更深層。
數形結合 深度 深化 深層
計算教學是小學數學的基本內容,也是學習其他數學知識的必要基礎。然而當下部分教師在平時的計算教學中,仍比較重視學生抽象思維的培養,忽視了學生形象思維的發展。要解決學生思維與能力之間的差異這一矛盾,最好的辦法就是為學生搭起一座橋梁——數形結合。
一、數形結合,讓計算情境更深度
新課標提出 “讓學生在生動具體的情境中學習數學”“讓學生在現實情境中體驗和理解數學”,因此,我們教師也應將計算教學置身于某個情境之中,使枯燥乏味的數學課充滿生趣和深度。
1.數形結合,讓情境有思維鋪墊
如在教學“分數乘整數”時,有教師就從整數乘法入手,設計活動情境:
同學們,折紙和涂色中有許多數學問題,今天,我們就拿起你的紙折一折,看看平均分成幾份?(八份)要求學生每次涂一份,涂五次。
問題一:每次涂了幾格?涂了幾次?你能用算式表示一共涂了幾格嗎?
讓學生帶著問題去觀察、交流,激活整數乘法的意義。為分數乘法做好鋪墊,從而自然遷移到新知中。
問題二:你能看出每次涂了這張紙的幾分之幾嗎?涂了幾次?用算式表示一共涂了這張紙的幾分之幾?
同樣的一張紙,從不同的角度來觀察,涂色部分就變成了分數,學生很輕松地感悟到了分數乘整數的意義,其原因就在于情境創設的鋪墊作用。
2.數形結合,讓情境有思維懸念
如我在教學“通分”時,為了激發學生通分的內在需求,我特意創設了這樣的教學情境:
師:小明過生日了,爸爸買了一個生日蛋糕,小明是個孝順的孩子,他想切這個蛋糕的送給爺爺奶奶,又將這塊蛋糕的送給爸爸媽媽,一共送了這塊蛋糕的幾分之幾呢?他應該怎樣切蛋糕呢?
請你們拿出一張圓片來代替蛋糕,用彩筆和尺在上面分一分。
學生拿起筆紛紛畫了起來,有的雙眉緊鎖不知如何下手,有的將它平分成兩份,又將它平分成三份。有的索性就一下子分成了六份……
教師展示學生的各種畫法,并引導學生討論、評價哪種方法更能一下子看出一共分了這塊蛋糕的幾分之幾。學生很容易看出一共分出六份。
教師順勢設置懸念:這樣的生活問題其實就是我們今天要學習的數學知識——通分。學生在這一疑問的驅使下,求知欲很強,就會自覺主動地投入到新課學習之中。
二、數形結合,讓算法探究更深化
1.數形結合,讓算法更直觀
如在教學《兩位數除一位數》時,課件呈現問題,學生列出算式:46÷2=?
師:46÷2=?請你算出過程,邊寫邊思考,并把過程寫在練習本上。
生:40÷2=20,6÷2=3,20+3=23。
師:誰和他的想法一樣?誰能介紹一下這種算法。
指名回答。
師:這種算法對不對呢?我們用小棒來驗證一下。
生用46根小棒分一分,指名一人邊操作邊說思考過程。
(在黑板上展示先將4捆小棒平均分成2份,再把6根小棒平均分成2份)
師:這種擺法和口算有什么聯系?
生:都是把46平均分兩次。
師:怎樣在豎式中把兩次分的過程清晰地表示出來呢?
師:剛才我看到有幾位同學是這樣表示的,同學們覺得有沒有道理?誰來評價一下?
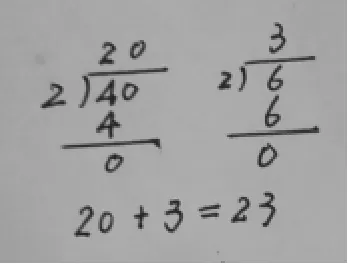
生1:我覺得有道理。第一個豎式表示4捆小棒平均分成2份,第二個豎式表示6根小棒平均分成2份。
生2:有道理,但是覺得有點麻煩。
師:同學們想象一下,分兩次就寫兩個豎式,分三次就得寫三個豎式……這樣,確實有點麻煩,有沒有好的建議呢?
生:把兩個豎式融合在一起。
師:請同學們來看這位同學只寫了一個豎式。
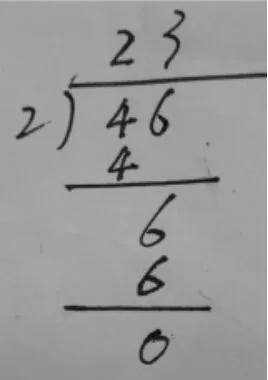
你能解釋一下嗎?
師:同學們再來看這位同學的。誰看懂了?兩個圓圈是什么意思?
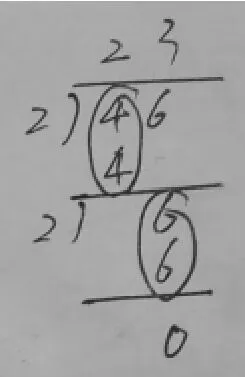
生:一個圈表示分了一次,兩個圈表示分了兩次。
師:比較這兩個豎式,有什么不同?
生:雖然都表示分了兩次的過程,但第一個豎式比較簡潔,而第二個豎式就重復了。
在上述過程中,將學生的操作過程與除法豎式的意義有機結合起來。教師投石擊水:“怎樣在豎式中把兩次分的過程清晰地表示出來?”學生自覺將直觀過程抽象成豎式,在比較分析、逐步完善中完成了豎式的建構。有了圖形的支撐,學生對算理的理解就能進一步走向全面和深刻。
2.數形結合,讓算法更優化
例如,數學“兩位數加一位數的進位加法”時,教師創設問題情境,學生順理成章地正確列出算式,27+5=?
結果很大一部分學生都異口同聲地說:“等于32。”
生1:27+5,我是這樣想的,7+5=12,20+12=32。
生2:我先算5+5=10,再算22+10=32。
生3:我用豎式計算。
根據學生回答,教師完成如下豎式板書。
面對這一系列的回答,教師明白“學生大部分都會做了”,這時,如何調動學生主動、積極地思考,調動學生解決問題的熱情呢?于是,教師立即追問:“27+5為什么會等于32呢?誰能用小棒幫助我們理解一下?讓學生把各種算法展示出來。
學生拿起小棒在桌上擺了起來。先擺2捆另7根,再擺5根,有的學生將7根和5根中的3根合并起來,扎成一捆,一共是32根;有的學生從7根里拿出5根和另5根放在一起湊成十根;還有的學生一根一根地加進去,邊數28 29、30、31、32。
教師讓學生上臺操作,并將滿十根扎成一捆的過程放慢呈現,相機提問,并讓學生比較各種方法,多中選優,擇優而用。學生經過逐步領悟、自我體驗、自我選擇判別選擇的能力得到了提高,思維向縱深處發展。
三、數形結合,讓計算練習更深層
計算課的練習不能一味地讓學生機械做題,這樣會讓學生覺得枯燥乏味。因此,我們可以讓數形結合,讓計算練習的設計更深層次一些。
1.數形結合,讓練習更明晰
如學了《有余數的除法》,一位教師設計這樣的練習:
師:通過剛才的活動,我們初步認識了有余數的除法,接下來,請同學們拿出小棒玩個游戲。
每人準備16根小棒放在桌面上,要求:用這些小棒擺幾個完全一樣的圖形,看看擺了幾個,有沒有剩余?并思考可以用什么除法算式來表示,把它寫在練習紙上。
(ΔΔΔΔΔ |16÷3=5……1)
(□□□□ 16÷4=4)
(荇荇荇 |16÷5=3……1)
(荏荏 ||||16÷6=2……4)
……
教師巡視,并展示幾位同學的作品,進行交流。
在這一練習過程中,將數學知識融入直觀操作中,借助動手操作,進行圖形表征,既展示正好平均分的情況,又展示了有余數的情形。這樣數形結合的練習形式,開放自主,不但鞏固、強化了圖形與算式的融合,而且也滲透、拓展了已建立的除法模型。
2.數形結合,讓練習更靈活
通過觀察圖形,學生不難想到,要求它們的和,只要把大正方形的面積減去剩下部分的面積,從而得出簡便的算法。
教師再以此為基礎,進行拓展,學生就能輕松地解決。
這一過程,絕不是簡單的模仿與記憶,而是將抽象的純數學知識轉化為具體形象的、便于學生理解的表象,從而將數與形有機結合起來,發展學生思維的靈活性。
我國著名數學家華羅庚先生說過:“數缺形時少直觀,形少數時難入微,數形結合百般好,隔裂分家萬事休。”在計算教學中,數形結合思想是一種可使復雜問題簡單化、抽象問題具體化的常用的數學思想方法。要想提高學生運用數形結合思想的能力,需要教師耐心細致地向學生滲透這一思想,引領學生走進數學的神奇殿堂!
[1]俞秉鈞.“數與代數”領域學生圖形直觀能力的培養[J].教學與管理,2016(10).
[2]楊凱.也談幾何直觀的教學價值[J].教育研究與評論,2016(8).

