原子核液滴模型結合能的薄壁近似驗證
楊清志,孫式運
(亳州職業技術學院,安徽 亳州 236800)
原子核液滴模型結合能的薄壁近似驗證
楊清志,孫式運
(亳州職業技術學院,安徽 亳州 236800)
原子核的液滴模型因諸多優點目前被廣泛接受和應用,但液滴模型的結合能及其修正公式主要來自實驗修正,缺乏明確的理論依據.針對這種現象,以薄壁近似為基礎,運用數學物理方法,從理論上推導了原子核液滴模型結合能公式,使其具有明確的物理意義,佐證了原子核液滴模型的正確性.
薄壁近似;液滴模型;結合能
為了進一步研究原子核的組成結構,核物理學家們提出了多種原子核的結構模型,主要有液滴模型、殼層模型、統計模型、光學模型等[1].其中液滴模型因物理意義明確、簡便適用等優點被廣泛接受和應用.但是針對原子核液滴模型結合能的修正項,目前主要是通過實驗給出的經驗修正,缺少明確的理論依據.據此,本文以薄壁近似為基礎,運用數學物理的方法,從理論上推導了原子核液滴模型結合能及其修正項公式,從而使公式具有明確的物理意義,在一定程度上證明了原子核液滴模型的正確性.
1 原子核的液滴模型
把原子核比作一個液滴,是因為原子核與液滴有相似的地方,一是核的結合能E正比于核子數A,即比結合能近似為常數,說明核子間相互作用力具有飽和性,與液體分子間作用力具有飽和性相類似;二是和物質的密度近似為常數,說明核不可壓縮,這也與液體相似[2].
因為原子核中的質子是帶正電的,所以應將其看作一個帶電液滴,核結合能為:
E=EV+ES+EC
(1)
式中EV為體積能,ES為表面能,EC為庫侖能.下面來推導核結合能的表達式,并利用薄壁近似加以證明.
2 球形核的結合能
對于球形核,滿足:
R=r0A1/3
(2)
(3)
式中R為核半徑,r0為核子半徑,ρ0為核子數密度,A為核子數.由此可得:

(4)

(5)

設質子在半徑為R的核內均勻分布,由電動力學可知它在距核中心r′處產生電位:
設第二個質子也在核內均勻分布,這兩個質子相互作用的靜電能為:

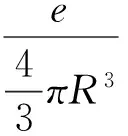

(6)
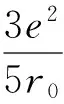
Ed=-adZ2/A
(7)
把(4)、(5)、(6)、(7)式帶入(1)式得:

(8)
上式即為原子核液滴模型的結合能.但需要指出的是,這只是對于球形核的主要幾項能量表達式.一般情況下原子核不是球形,質子也不是均勻分布的,還需要進行進一步修正[4].
3 利用薄壁近似驗證結合能公式
液滴模型認為在液滴內部有著均勻的密度分布,而在邊界密度突變為零.但原子核的密度在邊界不會突變為零,應有一層彌散層.設彌散層厚度遠小于核半徑,稱為薄壁近似條件,當核子數A?1時,此條件可以滿足.下面利用薄壁近似來驗證液滴模型結合能公式.
設體系基態核力作用的平均能量密度可表示為f(ρn,ρp,▽ρn,▽ρp),則體系結合能為:
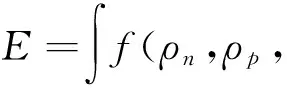
(9)
式中ρn、ρp為中子和質子能量密度,EC′為質子的庫侖能,▽ρn和▽ρp為其梯度.對ρn、ρp作薄壁近似,在核內部ρn、ρp為常數,梯度為零,即:
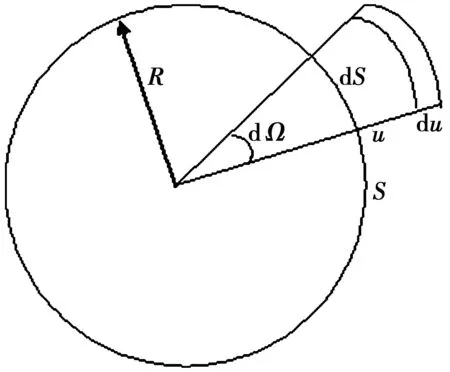
圖1 關于V及V′積分示意圖
而在邊界層f迅速減為零.在核邊緣取一等面積S,所包圍體積V,此體積之外空間為V′,則(9)式化為:
(10)
如圖1所示,與面積S垂直的距離設為u,則體積元dτ為:
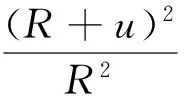
(11)
式中Ω為立體角,u在S處取正值,S內取負值.可認為f、f-f0均為u的函數,從而(11)式可進一步化簡:
將上式忽略高階無窮小(即后兩項)帶入(10)式得:
(12)
從式(12)可以看出,第一項對應體積能,第二項對應面積能,與(1)式描述相一致.可見,液滴模型忽略了平均曲率項及與A無關項,從數學角度即忽略高階無窮小,也是一致的.
再來討論庫侖能.質子間庫侖能一般表達式是:
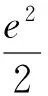
設ρl為液滴模型的電荷密度,則上式質子間庫侖能可展開為:
式中第一項為帶電液滴的庫侖能EC,第二項可看作是對彌散層的修正Ed,第三項為高階無窮小,同樣可忽略.因此上式可改寫為:
EC′=EC+Ed
(13)
再來看修正項Ed表達式:
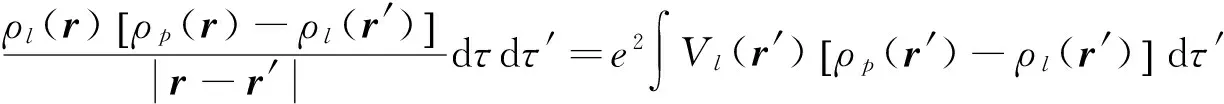
(14)
式中Vl(r′)為液滴模型電荷分布在r′處電位:
對于球形核,由圖1:
由于ρp(r)-ρl(r)只在u=0附近才有值,將Vl在u=0附近展開:
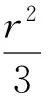
上式忽略高階無窮小得:
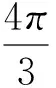
(15)
又由:

(16)
(17)
將(15)、(16)、(17)式帶入(14)式解得:
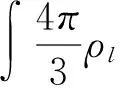
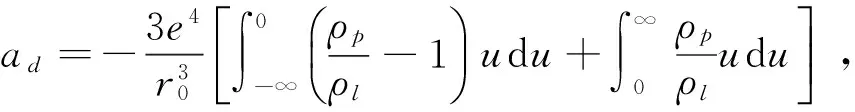
Ed=-adZ2/A
(18)
(18)式與(7)式關于庫侖能彌散層的修正形式上完全一樣.
4 小 結
以上是對于原子核液滴模型結合能的討論并利用薄壁近似加以驗證,在一定程度上佐證了液滴模型的正確性.雖然液滴模型并未給出原子核中質子與中子究竟是怎么排列與構建原子核的,但在解釋核素質量分布、β衰變、核裂變等方面都非常成功,因而獲得了推廣和應用[5][6].
[1]曹向陽.原子核中處理對關聯方法的研究[D].合肥:安徽大學,2014.1.
[2]褚圣麟.原子物理學[M].北京:高等教育出版社,1979:328.
[3]胡濟民,鐘云霄.原子核的宏觀模型[M].濟南:山東科學技術出版社,1998.
[4]盧水旺.原子核模型的研究[J].技術物理教學,2003(01):20-21.
[5]曾謹言,林純鎮,楊福家.原子核質量公式的分項檢驗[J].高能物理與核物理,1981(02).
[6]張海飛,包小軍,王佳眉,等.推廣的液滴模型及其應用[J].原子核物理評論,2013(03):241-259.
[責任編輯:徐明忠]
Thethin-walledapproximationvalidationofdropletmodelofnuclei’bindingenergy
YANG Qingzhi,SUN Shiyun
(Bozhou Vocational and Technical College,Bozhou 236800,China)
The droplet model of nuclei has been widely accepted and applied in many aspects,but the binding energy of the droplet model and its correction formula are mainly from the experimental correction,and lack of clear theoretical basis.In view of this phenomenon,using the methods of mathematical physics based on the thin-walled approximation,derived the formula of the droplet model of nuclei ’ binding energy in theory,it has a clear physical meaning,to prove the correctness of the droplet model of nuclei.
thin-walled approximation;droplet model;binding energy
2017-01-11;
2017-02-09
楊清志(1974—),男,安徽肥東人,亳州職業技術學院副教授,碩士,主要從事大學物理教學與研究.
O571.2
A
1672-3600(2017)12-0024-03

