聚焦常見的函數模型及應用
■天津市南開中學高二(1 3)班 李稀琰
聚焦常見的函數模型及應用
■天津市南開中學高二(1 3)班 李稀琰
解決函數模型的關鍵有兩點:一是實際問題數學化,即在理解的基礎上,通過列表、畫圖,引入變量,建立直角坐標系等手段把實際問題翻譯成數學問題,把文字語言翻譯成數學符號語言。二是對得到的函數模型進行解答,得出數學問題的解,要注重數學能力的培養。
一、構建二次函數模型
例1 某商場出售某種商品,每天可賣1000件,每件獲利4元。據經驗,若每件少賣1角錢,則每天可多賣1 0 0件,問:每件應減價多少元,才能獲得最大利潤?
解析:設每件少賣x角錢,每天利潤為y元,依題意得y=(10 0 0+1 0 0x)(4-0.1x)=-1 0x2+3 0 0x+40 0 0=-1 0(x-1 5)2+62 5 0,當x=1 5時,y有最大值。
二、構建分段函數模型
例2 通過研究學生的學習行為,專家發現,學生的注意力隨著老師講課時間的變化而變化,講課開始時,學生的興趣激增;中間一段時間,學生保持較理想的狀態,隨后學生的注意力開始分散。設f(t)表示學生注意力隨時間t(分鐘)的變化規律,f(t)越大,表明學生注意力越集中,經實驗分析得知:
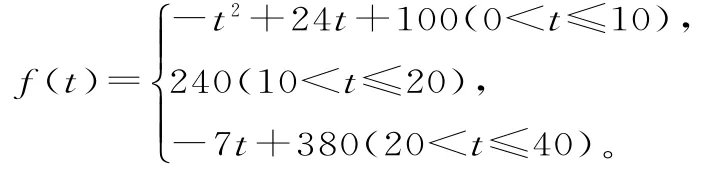
(1)問:講課開始多少分鐘,學生的注意力最集中?能持續多少分鐘?
(2)講課開始后5分鐘與講課開始后2 5分鐘比較,何時學生的注意力更集中?
(3)一道數學難題,需要講解2 4分鐘,并且要求學生的注意力至少達到1 8 0,那么經過適當安排,老師能否在學生達到所需的狀態下講完這道題目?
解析:(1)當0<t≤1 0時,f(t)=-t2+2 4t+1 0 0是增函數,當1 0<t≤2 0時,f(t)=-t2+2 4t+1 0 0是減函數且f(1 0)=f(2 4)=2 4 0,所以講課開始1 0分鐘,學生的注意力最集中,能持續1 0分鐘。
(2)求函數值比較,f(5)=1 9 5,f(2 5)=2 0 5,講課開始后2 5分鐘比講課開始后5分鐘學生的注意力更集中。
(3)當0<t≤1 0時,f(t)=-t2+2 4t+1 0 0=1 8 0,得t=4。當2 0<t≤4 0時,f(t)=-7t+3 8 0=1 8 0,得t=2 8.5 7,則學生注意力在1 8 0以上所持續的時間為2 8.5 7-4=2 4.5 7>2 4,所以,經過適當的安排,老師可以在學生達到所需要的狀態下講授完這道題。
三、構建指數函數模型
例3 某林場現有木材3萬立方米,如果每年平均增長5%,問:大約經過多少年該林場的木材量可增加到4萬立方米?
解析:經過x年,木材量y=3(1+5%)x,由題意得3(1+5%)x=4,即1.0 5x=,兩邊同取常用對數得
四、構建無理函數模型
例4 某自來水廠的蓄水池中有4 0 0噸水,水廠每小時可向蓄水池注水6 0噸,同時蓄水池又向居民小區供水,t小時內供水為1 2 0 6t噸(0≤t≤2 4)。
(1)多少小時后蓄水池中的水量最少?
(2)若蓄水池中水量少于8 0噸時,就會出現供水緊張現象,請問:每天有幾小時出現這種現象?
解析:(1)設t小時后蓄水池水量為y噸,則y=4 0 0+6 0t-1 2 0 6t(0≤t≤2 4)。令x=6t,0≤x≤1 2,則y=4 0 0+1 0x2-1 2 0x=1 0(x-6)2+4 0,當x=6,即t=6時,y有最小值4 0噸,所以供水6小時,水池中的水最少為4 0噸。
(2)由4 0 0+1 0x2-1 2 0x<8 0,解得0<x<4,即0<<4,解得故每天有8小時供水緊張。
(責任編輯 劉鐘華)

