淺談線性遞推數列求通項問題
■安徽省合肥市第八中學高二(3 4)班 聶羽丞
淺談線性遞推數列求通項問題
■安徽省合肥市第八中學高二(3 4)班 聶羽丞
數列是高中數學的重要內容之一,因其形式多樣,解法靈活,也是自主招生和數學競賽考查的重點。本文討論了線性遞推數列求通項問題的一些常用解法,希望能給同學們在學習這部分知識的時候提供一些幫助。
一、齊次線性遞推數列求通項
定理1:若x1,x2為遞推關系an=p an-1+q an-2(n=2,3,…)的特征方程的兩根,則:
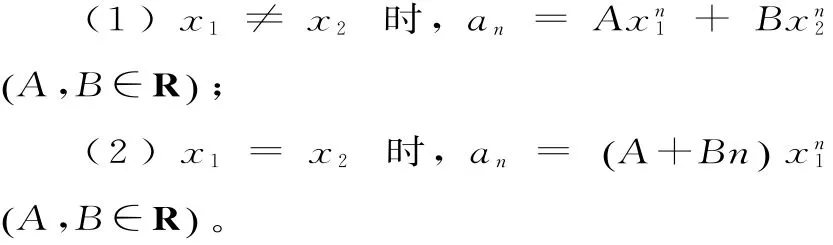
其中A,B可由初始條件確定。
定理2:k階常系數齊次線性遞推數列an+k=α1an+k-1+α2an+k-2+…+αn-1ak+1+αnak的特征方程為+αn-1x+αn,該方程的全部根為x1(k1重根),x2(k2重根),…,xm(km重根),其中k1+k2+…+km=n且ki∈N*,則
以上我們找到了常系數齊次線性遞推數列的一般解法,那么對于非齊次的情況又如何處理呢?
二、非齊次線性遞推數列求通項
1.含關于n的多項式型問題

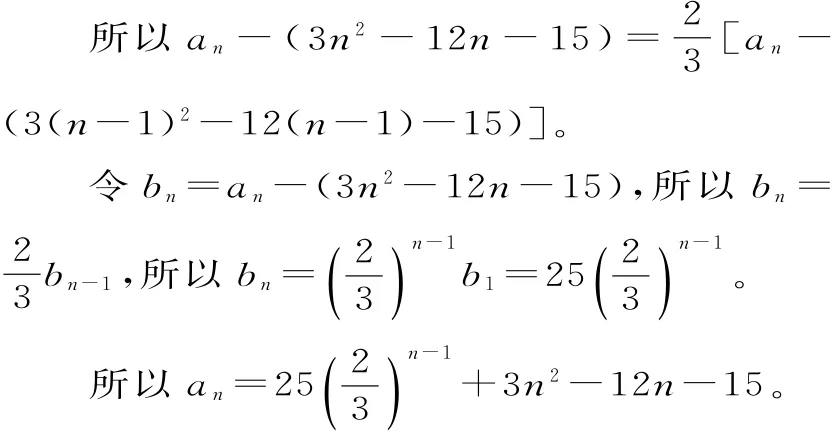
總結:解決含關于n的多項式的遞推數列問題時,可將關于n的多項式合理拆分,從而得到等比數列。本方法對于解決該類問題具有一定的普遍性。拆分方式由待定系數法確定。
2.“齊次+常數”型問題

總結:寫出相鄰的遞推式并做差,能得到常系數齊次線性遞推數列,利用特征根法易于求解,這是該類問題的常用解法。
3.含根式型問題
這類題目通常有多種不同情況。
例3 已知數列{an},a1=1且an+1=

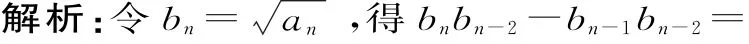

總結:遞推公式中存在根式時難以處理,將根式換作某一新數列是一種常用方法;出現根式時的第二種常用方法就是直接平方,這種情況下能夠轉化為“齊次+常數”型問題,易于求解;解決這一類問題時,換元法與直接平方法各有所長,有時換元法一目了然,有時直接平方更為巧妙,但具體問題需具體對待。
4.一些特殊方法

總結:這一類問題沒有通用解法,需要我們注意遞推式的特點,同時還要活學活用其他數學知識。
(責任編輯 劉鐘華)
編后語:在學習的過程中,你一定會遇到許多問題,也需要解決這些問題,而在解決問題的過程中,如果能深入一些、細致一些,就會有新的發現,把你的發現寫出來就是一篇論文。希望同學們在學習過程中要善于發現和總結,同時也希望同學們把論文寄給我們。電子信箱:xuexifaxian@126.com。

