數列的求和
■江西省豐城中學 吳愛龍
數列的求和
■江西省豐城中學 吳愛龍
編者的話:基本知識和基本技能是高中數學的核心,同學們一定要高度重視。愿同學們通過閱讀,能從中感悟知識的結構與拓展,把握高考命題特點與趨勢。
2.已知Sn,求an。
已知數列的前n項和Sn,求數列的通項an時,我們有關系式
3.等差數列的前n項和。
一、考綱要求
掌握等差數列、等比數列的前n項和公式。
二、知識梳理與拓展
1.數列的前n項和。
數列的前n項和通常用Sn表示,其意義是指Sn=a1+a2+…+an。
數列的前n項和是一個專用述語,有其特指的含義。必須理解好三點:①指的是和,而不是n項之積或別的運算。②指的只能是n個項之和,不能多一項或少一項。③指的是前n項之和,而不是某n個項的和,應從第一項開始,一項不少地加至第n項。如果不是從第一項開始,而是從某項開始的連續n項之和,盡管不是數列的前n項和,但也可以借助Sn來表示,比如a3+a4+…+an+2可以表示為Sn+2-S2;也可以用求和符號∑來表
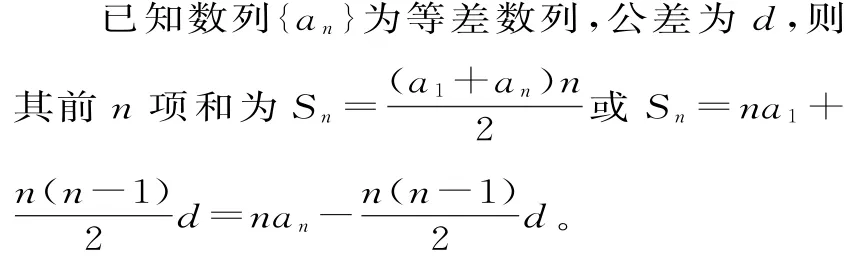
上述第一個公式可由倒序相加法推導。其實它表示上底邊長為a1,下底邊長為an,高(層數)為n的梯形面積公式;而后兩個公式則是將該梯形割或補,變成一個平行四邊形的面積na1與一個三角形的面積d之和或變成一個平行四邊形的面積nan與一個三角形的面積之差了。特別地,當d=0時,其前n項和Sn=na1。
4.等比數列的前n項和。
已知數列{an}為等比數列,公比為q,則的“ai”是代表項,它代表了a3,a4,…,an+2中的任一項,而∑下方的“i=3”是指求和時從第三項a3開始相加,∑上方的“n+2”指的是最后加至第n+2項an+2終止。這個符號既清晰又簡捷,在高等數學中還可以直接參與運算。在初等數學研究方面,常用∑表示循環和,如三角形ABC的三邊分別為a、b、c,則其周長可以表示為∑a,即∑a=a+b+c。
如果數列從第一項開始一項不少地加下去,直至無窮,這個和被稱作是無窮數列的所有項和,常記為S;任何數列都存在著前n項和,卻未必有所有項之和了。當等比數列的公比q滿足|q|<1且q≠0時,其所有項之
常數列既是等差數列,又是等比數列,不論從等差或等比角度看都有Sn=na1。
上述公式可由錯位相減法推導,也可以用下面幾種方法推得。
方法1:Sn=a1+q(a1+a1q+…+aqn-2)=a1+qSn-1=a1+q(Sn-an)=a1+q(Sn-a1qn-1),n≥2,q≠1。所以Sn=時,亦符合。
方法2:設等比數列{an}的公比q≠1,則

由合比定理有:5.等差(比)數列前n項和的主要性質。

(2)等差數列中,當a1>0,d<0時,若ak>0,ak+1<0,則Sk最大;當a1<0,d>0時,若ak<0,ak+1>0,則Sk最小。
(3)等差(比)數列中,非零數列Sk,S2k-Sk,S3k-S2k,…仍成等差(比)數列。
6.數列求和的幾種常見方法。
數列求和的常用方法有:倒序相加法、錯位相減法、裂項相消法、公式法、分組求和法、奇偶數討論法等。
三、典例解析與點評

點評:對此解法應注意兩點:(1)等差數列前n項和Sn是關于n的沒有常數項的二次函數,因此若設Sn=k(7n+2),Tn=k(n+3),則是不合理的;(2)已知數列的前n項和Sn,求數列的通項an時,有關系式an=
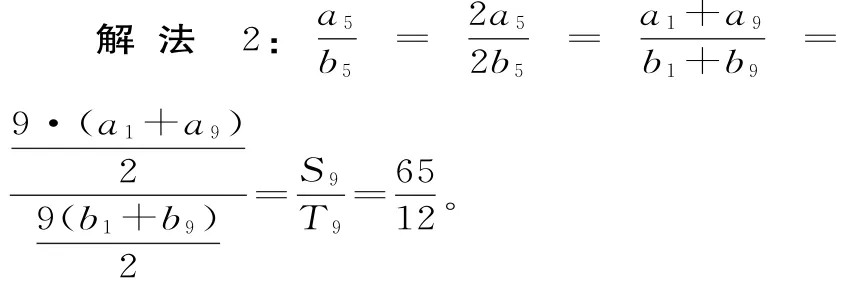
點評:對此解法也應注意兩點:(1)等差數列的性質的靈活運用;(2)等差數列求和公式的逆用。

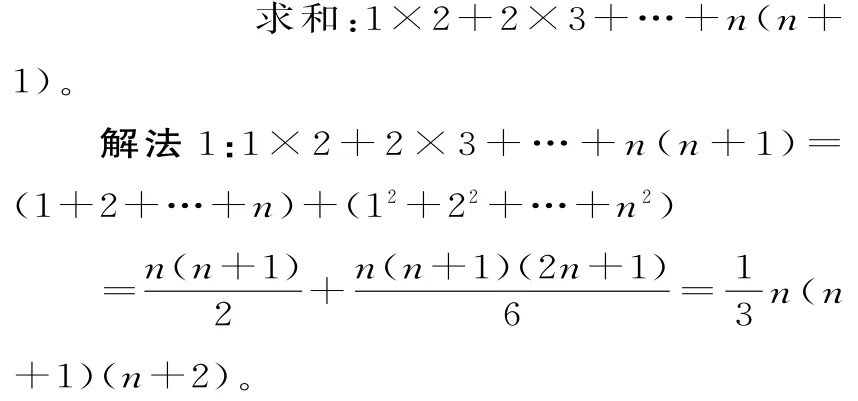
點評:此法是分組求和與公式法求和的完美組合。常用的幾個公式

點評:上述方法用的是裂項相消法,裂項(拆項)相消法是數列求和的常用方法之一。裂項是手段,相消是目的。因此,尋找合理的裂項方式是關鍵。例如一項裂成了兩項,但由于無法相互抵消其中的項,所以這種裂項是失敗的。對幾種常見的裂項應熟記。此外,相消時規律性很強,既然是成對地“裂”,又是成雙地“消”,所以必定是成套地“留”。
解法3:學了組合,也可用組合數性質來解。因為n(n+1)=2C2n+1,又Cmn+1=Cmn+Cm-1n,所以1×2+2×3+…+n(n+1)=(n+2)。
點評:此解法將數列求和問題轉化為組合數求和并利用組合數性質的問題來解,可謂匠心獨運。
一般地,我們有1·2·3·…·k+2·3·4·…·(k+1)+…+n(n+1)(n+2)…(n+k)(n,k∈N*,k≥2)。求和S=1+2x+3x2+…+nxn-1。
當x≠0且x≠1時,有:
S=1+2x+3x2+…+nxn-1。
xS=x+2x2+…+(n-1)xn-1+nxn。

點評:上述解法是分類討論思想與化歸思想的完美組合,解題時極易漏掉x=0與x=1時情形的討論。錯位相減法,“錯位”是手段,“相減”是目的;如果錯位后不能相減,錯位就是無功之舉;如果錯位相減后能將各項系數歸一,則錯位就是一種漂亮的形式,因為采用錯動位置的書寫方法是為了將字母x的指數對齊,對整齊后再減才會少出錯誤。話雖如此,但很多同學具體運用此法時仍會出錯,很難對上正確答案,因此我們平時應多加訓練。網絡上流行一種死記結論的待定系數法,但筆者不推薦使用這種方法。

點評:這里對已知等式兩邊求導,體現了整體處理思想,當然也可以對所求和式通過求積分的辦法求得。有時可能需要多次求導或求積分。
(責任編輯 徐利杰)

