正、余弦型函數的解題功效
2017-11-27 09:15:28河南省沈丘縣第二高級中學高二23阮熙杰
中學生數理化(高中版.高二數學) 2017年10期
■河南省沈丘縣第二高級中學高二(23)班 阮熙杰
正、余弦型函數的解題功效
■河南省沈丘縣第二高級中學高二(23)班 阮熙杰
正弦型函數y=Asin(ωx+φ)及余弦型函數y=Acos(ωx+φ),是探究三角函數圖像與性質的一個中轉站,也就是說我們解答有關三角函數圖像與性質的問題,都要先把三角函數化為正弦型函數y=Asin(ωx+φ)或余弦型函數y=Acos(ωx+φ),然后再具體情況具體分析。
一、結合三角函數周期性確定對稱軸

點評:正弦型函數的對稱軸都經過正弦型函數圖像的最高點或最低點,因此,如果是選擇題,當我們獲取正弦型函數解析式后可以通過檢驗的方法確定對稱軸方程,即把答案中所給的直線方程代入正弦型函數解析式y=Asinωx+φ(),看所得函數值是否為±A。如果所得函數值為A或-A,則可確定該直線方程即為一條對稱軸方程。
二、結合三角函數單調性確定參數ω的值


三、結合三角函數奇偶性確定參數值

四、結合三角函數圖像平移確定初相

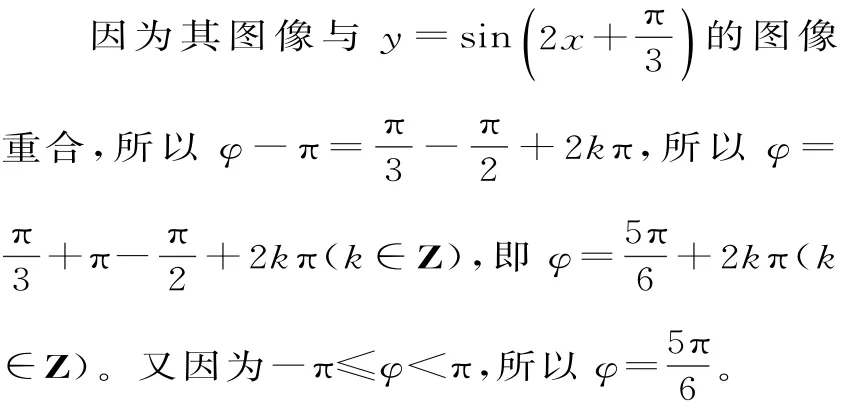
點評:當兩個正弦(或余弦)型函數圖像重合時,振幅與ω要相同,但是兩個初相之間相差2kπ(k∈Z)個單位,即若y=Asin(ωx+φ1)與y=Asin(ωx+φ2)的函數圖像重合時,則φ1=φ2+2kπ(k∈Z)。
(責任編輯 趙 平)

