由遞推關系式求數列通項公式的常見方法

■河南省鄭州市第四十七中學 呂 茵

由遞推關系式求數列通項公式的常見方法

■河南省鄭州市第四十七中學 呂 茵

編者的話:經典題突破方法quot;欄目里例、習題選名校模擬題或三年高考真題,推出本欄目的主要目的是讓同學們更好地領悟數學解題思想方法,通過多解多變培養同學們多思多想的好習慣。學會解題反思,無疑是同學們學習的一條捷徑,愿同學們不斷在反思中進步,在反思中收獲!

數列是高中數學的重要內容之一,數列的通項公式是數列的核心之一。在很多情況下,各種數列綜合問題的解決,首先是對數列通項公式的求解,這是解決數列綜合問題的突破口和關鍵。目前我們比較熟悉的數列有:等差數列、等比數列、等和數列、等積數列及其廣義形式。求解等差數列、等比數列的通項公式的方法是累加和累乘,這兩種方法是求數列通項公式的最基本方法。求數列通項的基本思路是把所求數列通過變形,轉化為等差數列或等比數列。目前用遞推關系求數列通項公式的方法有:累加法、累乘法、待定系數法、對數變換法、倒數變換法、換元法(目的是去掉遞推關系式中出現的根號)、不動點法(遞推式是一個數列通項的分式表達式)、特征根法等。

一、公式法

已知數列{an}滿足an+1=2an+3×2n,a1=2,求數列{an}的通項公式。

二、累加法

1.適用于:an+1=an+f(n)——這是廣義的等差數列,累加法是最常見的方法之一。

2.若an+1-an=f(n)(n≥1),則:a2-a1=f(1);

a3-a2=f(2);

…

an+1-an=f(n)。

已知數列{an}滿足an+1=an+2×3n+1,a1=3,求數列{an}的通項公式。

解析:由an+1=an+2×3n+1,得an+1-an=2×3n+1,則an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+(a2-a1)+a1

=(2×3n-1+1)+(2×3n-2+1)+…+(2×32+1)+(2×31+1)+3

=2(3n-1+3n-2+…+32+31)+n+2

=3n-3+n+2

=3n+n-1。

所以an=3n+n-1。

三、累乘法

1.適用于:an+1=f(n)an。

已知數列{an}滿足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),求{an}的通項公式。

解析:由題意知an=a1+2a2+3a3+…+(n-1)an-1(n≥2)。 ①

因此,an+1=a1+2a2+3a3+…+(n-1)an-1+nan。 ②

②-①得:

an+1-an=nan。

則an+1=(n+1)an(n≥2)。

已知an=a1+2a2+3a3+…+(n-1)an-1(n≥2),取n=2得a2=a1。

又知a1=1,則a2=1,代入③得:

四、待定系數法，適用于an+1=qan+f(n)

已知數列{an}滿足an+1=3an+5×2n+4,a1=1,求數列{an}的通項公式。

解析:設an+1+x×2n+1+y=3(an+x×2n+y)。 ①

將an+1=3an+5×2n+4代入①式,得:

3an+5×2n+4+x×2n+1+y=3(an+x×2n+y)。

整理得:

(5+2x)×2n+4+y=3x×2n+3y。

由a1+5×21+2≠0及②式,得:

an+5×2n+2≠0。

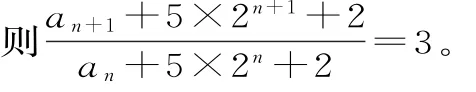
數列{an+5×2n+2}是以13為首項,3為公比的等比數列,因此an+5×2n+2=13×3n-1,則an=13×3n-1-5×2n-2。

點評:解本題的關鍵是把遞推關系式an+1=3an+5×2n+4轉化為an+1+5×2n+1+2=3(an+5×2n+2),從而可知數列{an+5×2n+2}是等比數列,進而求出數列{an+5×2n+2}的通項公式,最后再求數列{an}的通項公式。

五、對數變換法，適用于an+1=parn(p,r為常數)型,p＞0,an＞0

數列{an}滿足an+1=2×3n×a5n,a1=7,求數列{an}的通項公式。

解析:因為an+1=2×3n×a5n,a1=7,所以an＞0,an+1＞0。在an+1=2×3n×a5n的兩邊取常用對數,得lgan+1=5lgan+nlg3+lg2。 ①

不妨設lgan+1+x(n+1)+y=5(lgan+xn+y)。 ②

將①式代入②式,得5lgan+nlg3+lg2+x(n+1)+y=5(lgan+xn+y)。

兩邊消去5lgan并整理,得:(lg3+x)n+x+y+lg2=5xn+5y。

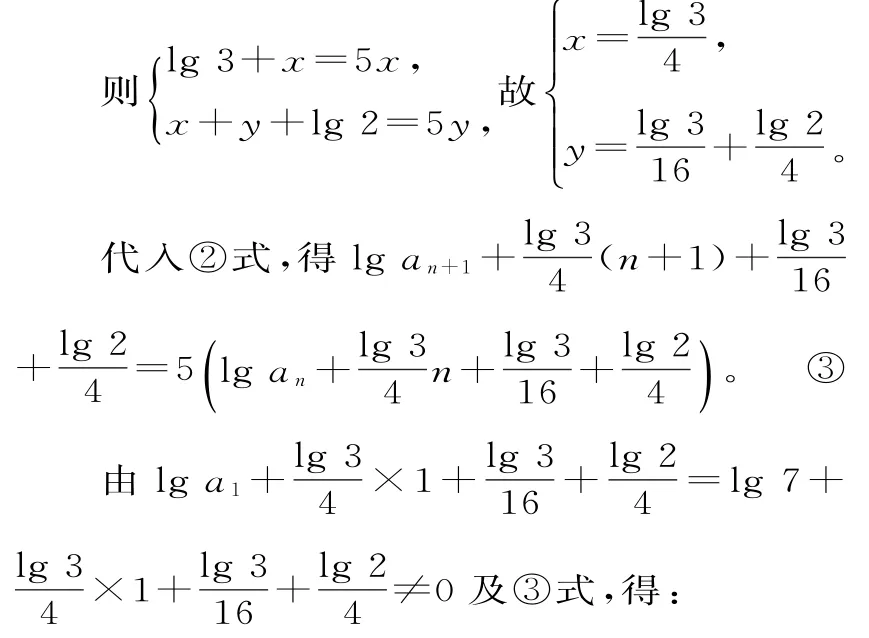
六、換元法

點評:解本題的關鍵是將 1+24an換元為bn,使得所給遞推關系式轉化為bn+1=的形式,從而可知數列{bn-3}為等比數列,進而求出數列{bn-3}的通項公式,最后求出數列{an}的通項公式。

七、倒數變換法，適用于分式關系的遞推公式，分子只有一項

八、不動點法

已知數列{an}滿足an+1=求數列{a}的通項公式。

n

九、特征方程法，適用于形如an+2=pan+1+qan(p,q是常數）的數列

形如a1=m1,a2=m2,an+2=pan+1+qan(p,q是常數)的二階遞推數列也可用特征根法求得通項an,其特征方程為:

x2=px+q。①

若①有兩個異根α,β,則可令an=c1αn+c2βn(c1,c2是待定常數)。

若①有兩個重根α=β,則可令an=(c1+nc2)αn(c1,c2是待定常數)。

再利用a1=m1,a2=m2,可求得c1,c2,進而求得an。

已知數列{an}滿足a1=2,a2=3,an+2=3an+1-2an(n∈N*),求數列{an}的通項公式。

解析:其特征方程為x2=3x-2,解得x1=1,x2=2。令an=c1·1n+c2·2n。

(責任編輯 徐利杰)