數(shù)列求和典型例題分析

■河南鄭州市第四十七中學(xué) 鞏建輝

數(shù)列求和典型例題分析

■河南鄭州市第四十七中學(xué) 鞏建輝

數(shù)列是高考中的熱點(diǎn)也是難點(diǎn)。從近五年高考試題分析來(lái)看,數(shù)列命題的基本特點(diǎn)是:試題題型規(guī)范,方法可循,難度穩(wěn)定在中檔。高考數(shù)列解答題主要題型有:等差、等比數(shù)列的綜合問(wèn)題;證明一個(gè)數(shù)列為等差或等比數(shù)列;求數(shù)列的通項(xiàng)及非等差、非等比數(shù)列的前n項(xiàng)和;證明數(shù)列型不等式。尤其是對(duì)數(shù)列求和的問(wèn)題考查較為突出,下面就對(duì)數(shù)列求和的典型問(wèn)題進(jìn)行總結(jié)。

一、基本數(shù)列求和方法

二、非基本數(shù)列求和的常用方法

(1)倒序相加法:如果一個(gè)數(shù)列{an}的前n項(xiàng)中與首末兩端等“距離”的兩項(xiàng)的和相等,那么求這個(gè)數(shù)列的前n項(xiàng)和即可用倒序相加法,例如利用倒序相加法可求得sin21°+sin22°+sin23°+…+sin288°+sin289°=44.5,再比如等差數(shù)列的前n項(xiàng)和公式即是用此法推導(dǎo)的。

(2)分組求和法:一個(gè)數(shù)列的通項(xiàng)公式是由若干個(gè)等差數(shù)列或等比數(shù)列或可求和的數(shù)列組成,則求和時(shí)可用分組求和法,分別求和后再相加減。如已知數(shù)列{an}的通項(xiàng)an=2n+(2n-1),求其前n項(xiàng)和Sn。

(3)并項(xiàng)求和法:一個(gè)數(shù)列的前n項(xiàng)和中兩兩結(jié)合后可求和,則可用并項(xiàng)求和法。如已知數(shù)列{an}的通項(xiàng)an=(-1)nf(n),求其前n項(xiàng)和Sn。

(4)錯(cuò)位相減法:如果一個(gè)數(shù)列的各項(xiàng)是由一個(gè)等差數(shù)列和一個(gè)等比數(shù)列的對(duì)應(yīng)項(xiàng)之積構(gòu)成的,那么這個(gè)數(shù)列的前n項(xiàng)和即可用錯(cuò)位相減法來(lái)求,如等比數(shù)列的前n項(xiàng)和公式就是用此法推導(dǎo)的。

(5)裂項(xiàng)相消法:把數(shù)列的通項(xiàng)拆成兩項(xiàng)之差,在求和時(shí)中間的一些項(xiàng)可以相互抵消,從而求得其和。

常見(jiàn)的裂項(xiàng)公式:

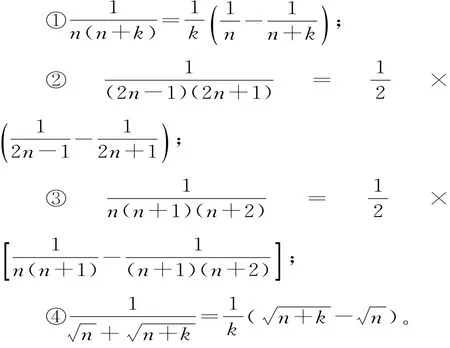
三、常用求和公式

四、典型例題分析

(一)分組求和與并項(xiàng)求和

已知等差數(shù)列{an}的前n項(xiàng)和為Sn,且a2=8,S4=40。數(shù)列{bn}的前n項(xiàng)和為T(mén)n,且Tn-2bn+3=0,n∈N*。

(1)求數(shù)列{an},{bn}的通項(xiàng)公式;

因?yàn)門(mén)n-2bn+3=0,故當(dāng)n=1時(shí),b1=3。

當(dāng)n≥2時(shí),Tn-1-2bn-1+3=0。

兩式相減得bn=2bn-1(n≥2)。

所以數(shù)列{bn}為等比數(shù)列。

故bn=3·2n-1。

解題心得:具有下列特點(diǎn)的數(shù)列適合分組求和:

(1)若an=bn±cn,且{bn},{cn}為等差數(shù)列或等比數(shù)列,可采用分組求和法求{an}的前n項(xiàng)和;

(二)錯(cuò)位相減法求和

已知數(shù)列{an}滿(mǎn)足a1=1,an+1=3an,數(shù)列{bn}的前n項(xiàng)和Sn=n2+2n+1。

(1)求數(shù)列{an},{bn}的通項(xiàng)公式;

(2)設(shè)cn=anbn,求數(shù)列{cn}的前n項(xiàng)和Tn。

解析:(1)由題意知數(shù)列{an}是首項(xiàng)為1,公比為3的等比數(shù)列,其通項(xiàng)公式為an=3n-1;數(shù)列{bn}滿(mǎn)足b1=S1=4,n≥2時(shí),bn=Sn-Sn-1=2n+1。所以,數(shù)列{bn}的通項(xiàng)公

(2)由(1)知cn=anbn=

故Tn=4+5×3+7×32+…+(2n+1)·3n-1。

3Tn=12+5×32+7×33+9×34+…+(2n+1)·3n。

兩式相減得:

-2Tn=7+2(32+33+34+…+3n-1)-(2n+1)·3n=-2-2n·3n。

所以Tn=n·3n+1(n≥2)。

綜上,數(shù)列{cn}的前n項(xiàng)和Tn=n·3n+1(n∈N*)。

解題心得:(1)一般地,如果數(shù)列{an}是等差數(shù)列,{bn}是等比數(shù)列,求數(shù)列{an·bn}的前n項(xiàng)和,可采用錯(cuò)位相減法求和,解題思路是:和式兩邊同乘等比數(shù)列{bn}的公比,然后作差求解。

(2)在寫(xiě)出“Sn”與“qSn”的表達(dá)式時(shí),應(yīng)特別注意將兩式“錯(cuò)項(xiàng)對(duì)齊”,以便下一步準(zhǔn)確寫(xiě)出“Sn-qSn”的表達(dá)式。

(三)裂項(xiàng)相消法求和

數(shù)列{an}的前n項(xiàng)和為Sn,且an是Sn和1的等差中項(xiàng),等差數(shù)列{bn}滿(mǎn)足b1=a1,b4=S3。

(Ⅰ)求數(shù)列{an},{bn}的通項(xiàng)公式;

解析:(Ⅰ)因?yàn)閍n是Sn和1的等差中項(xiàng),所以Sn=2an-1。

當(dāng)n=1時(shí),a1=S1=2a1-1,故a1=1。

當(dāng)n≥2時(shí),an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,故an=2an-1。

故an=2n-1,Sn=2n-1。

設(shè){bn}的公差為d,b1=a1=1,b4=1+3d=7,故d=2。

故bn=1+(n-1)×2=2n-1。

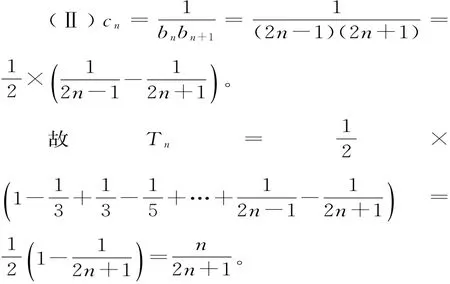
解題心得:裂項(xiàng)相消法的基本思想就是把a(bǔ)n分拆成an=bn+k-bn(k∈N*)的形式,從而達(dá)到在求和時(shí)絕大多數(shù)項(xiàng)相消的目的。在解題時(shí)要善于根據(jù)這個(gè)基本思想變換數(shù)列{an}的通項(xiàng)公式,使之符合裂項(xiàng)相消的條件。

知識(shí)小結(jié):

1.數(shù)列求和,一般應(yīng)從通項(xiàng)入手,若通項(xiàng)未知,先求通項(xiàng),再通過(guò)對(duì)通項(xiàng)變形,轉(zhuǎn)化為與特殊數(shù)列有關(guān)或具備某種方法適用特點(diǎn)的形式,從而選擇合適的方法求和。

2.解決非等差、非等比數(shù)列的求和問(wèn)題,主要有兩種思路:(1)轉(zhuǎn)化的思想,即將一般數(shù)列設(shè)法轉(zhuǎn)化為等差或等比數(shù)列,這一思想方法往往通過(guò)通項(xiàng)分解或錯(cuò)位相減來(lái)完成;(2)不能轉(zhuǎn)化為等差或等比數(shù)列的數(shù)列,往往通過(guò)裂項(xiàng)相消法、錯(cuò)位相減法、倒序相加法等來(lái)求和。但是在解題過(guò)程中還需注意:(1)直接應(yīng)用公式求和時(shí),要注意公式的應(yīng)用范圍。(2)在應(yīng)用錯(cuò)位相減法求和時(shí),注意觀察未合并項(xiàng)的正負(fù)號(hào)。(3)在應(yīng)用裂項(xiàng)相消法求和時(shí),要注意消項(xiàng)的規(guī)律具有對(duì)稱(chēng)性,即前面剩多少項(xiàng),后面就剩多少項(xiàng)。

(責(zé)任編輯 徐利杰)