利用奇異值分解的二階遞歸系統(tǒng)數(shù)值穩(wěn)定性方法

付波， 劉濟(jì)源， 趙熙臨， 徐光輝, 王子鵬

(湖北工業(yè)大學(xué) 電氣與電子工程學(xué)院， 湖北 武漢 430068)

利用奇異值分解的二階遞歸系統(tǒng)數(shù)值穩(wěn)定性方法

付波， 劉濟(jì)源， 趙熙臨， 徐光輝, 王子鵬

(湖北工業(yè)大學(xué) 電氣與電子工程學(xué)院， 湖北 武漢 430068)

為了簡(jiǎn)便地解決二階遞歸系統(tǒng)的穩(wěn)定性問(wèn)題，將二階遞歸系統(tǒng)轉(zhuǎn)變?yōu)槎A離散時(shí)變線性系統(tǒng)，并討論遞歸系統(tǒng)的穩(wěn)定性.在二階離散線性時(shí)變系統(tǒng)穩(wěn)定性分析的基礎(chǔ)上，利用奇異值分解(SVD)，將其轉(zhuǎn)化為參考信號(hào)(RS)系統(tǒng).提出一個(gè)新的離散時(shí)變線性系統(tǒng)不穩(wěn)定性的充分條件，并以離散正交Krawtchouk多項(xiàng)式與Jacobsthal數(shù)列遞歸式為主，討論并推導(dǎo)出其在Ⅱ,Ⅳ象限上的變化情況和新的不穩(wěn)定性判據(jù).仿真結(jié)果驗(yàn)證了結(jié)論的準(zhǔn)確性.

Krawtchouk多項(xiàng)式； Jacobsthal數(shù)列; 奇異值分解； 遞歸系統(tǒng)； 線性離散時(shí)變系統(tǒng)

遞歸是一種利用簡(jiǎn)單操作實(shí)現(xiàn)復(fù)雜運(yùn)算的有效方法，即通過(guò)簡(jiǎn)單的問(wèn)題來(lái)解決復(fù)雜的問(wèn)題[1].其表現(xiàn)形式較典型的是二階遞歸，即數(shù)列的某一項(xiàng)是由其前兩項(xiàng)計(jì)算所得[2-3].Legendre多項(xiàng)式、Chebyshev多項(xiàng)式、Jacobi多項(xiàng)式、Hermite多項(xiàng)式、Tchebichef多項(xiàng)式和Krawtchouk多項(xiàng)式等經(jīng)典正交多項(xiàng)式[4-6]在圖像正交矩、曲線擬合、非線性電路計(jì)算，以及計(jì)算結(jié)構(gòu)可靠性分析等技術(shù)都有應(yīng)用[7-8].但由于正交多項(xiàng)式解析式過(guò)于復(fù)雜，所以在實(shí)際應(yīng)用中一般采用其遞歸式求解多項(xiàng)式的值.Mukundan等[9]發(fā)現(xiàn)正交多項(xiàng)式的二階遞歸運(yùn)算有可能導(dǎo)致數(shù)值發(fā)散，Gautschi[10-11]討論了離散正交多項(xiàng)式的遞歸收斂性，關(guān)軼峰等[12]針對(duì)二階離散線性時(shí)變系統(tǒng)的穩(wěn)定性也做了大量研究.由于離散多項(xiàng)式不存在離散誤差，其精度與高階數(shù)值的傳遞有關(guān)，隨著階數(shù)的增大，多項(xiàng)式的數(shù)值和誤差的增大更導(dǎo)致其不穩(wěn)定，從而影響圖像重構(gòu)的精確性.Mukundan[13]利用x循環(huán)代替了n循環(huán)，同時(shí)，在一定程度上找到了高階多項(xiàng)式的誤差傳遞，解決了多項(xiàng)式高精度的算法問(wèn)題.張海艷等[14]在圖像分割、重構(gòu)的問(wèn)題上利用算法的穩(wěn)定性，提出了概率密度函數(shù)在生物信息學(xué)上的研究.本文在二階離散線性時(shí)變系統(tǒng)穩(wěn)定性分析的基礎(chǔ)上，利用奇異值分解(singular value decomposition,SVD)方法將其轉(zhuǎn)化為參考信號(hào)(reference signal,RS)系統(tǒng)，提出一個(gè)新的離散時(shí)變線性系統(tǒng)不穩(wěn)定性的充分條件，并通過(guò)實(shí)驗(yàn)驗(yàn)證其結(jié)果.

1 遞歸系統(tǒng)數(shù)值穩(wěn)定性

1.1穩(wěn)定性定義

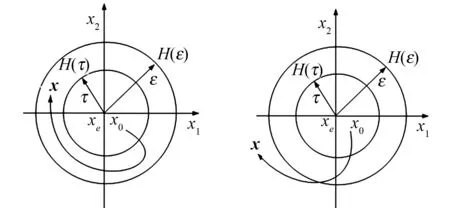
(a) 穩(wěn)定 (b) 不穩(wěn)定圖1 遞歸系統(tǒng)的穩(wěn)定性狀態(tài)Fig.1 Stability states of recursive systems

設(shè)系統(tǒng)初始狀態(tài)x0位于以平衡狀態(tài)xe為球心，半徑為ε的球域H(ε)內(nèi).如果對(duì)所考慮的整個(gè)時(shí)間區(qū)間內(nèi)，從H(ε)內(nèi)任一點(diǎn)x0出發(fā)的受擾運(yùn)動(dòng)φ(t，x0，xe)的軌跡都不超出H(ε)，則稱(chēng)xe=0在李雅普諾夫下穩(wěn)定，如圖1(a)所示.對(duì)某個(gè)εgt;0，在所有半徑為τ的球域H(τ)內(nèi)的初始狀態(tài)，至少存在一個(gè)初始狀態(tài)，使得從它出發(fā)的解始終不會(huì)限制在以ε為半徑的球域H(ε)里，則稱(chēng)平衡點(diǎn)在t0是不穩(wěn)定的，如圖1(b)所示.

1.2正交多項(xiàng)式

在矩函數(shù)集合中，分為連續(xù)正交多項(xiàng)式與離散正交多項(xiàng)式.Krawtchouk多項(xiàng)式是一種常見(jiàn)的離散正交多項(xiàng)式，更適合于對(duì)數(shù)字圖像的處理.n階Krawtchouk多項(xiàng)式的定義為

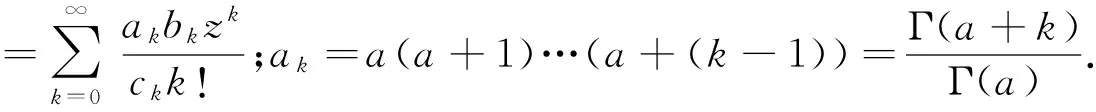
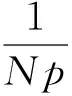
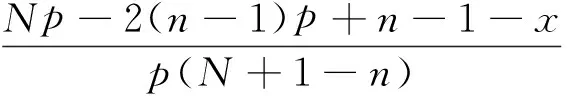
2 二階遞歸系統(tǒng)的SVD模型

2.1SVD方法

設(shè)2×2矩陣G∈C2×2，C為復(fù)數(shù)集，RankG=2，則存在2階酉矩陣U和2階酉矩陣V，使得

式(3)中：Σ=diag(σ1,σ2)，且σ1≥σ2≥0，而σi(i=1，2，)為矩陣G的正奇異值.

對(duì)狀態(tài)矩陣G(t)做SVD分解，可得G(t)=U(t)S(t)V(t)T.將U(t)，V(t)設(shè)定為單位旋轉(zhuǎn)矩陣，又因?yàn)閄(t)=G(t)X(t-1)，則有

將式(4)展開(kāi)可得

重新定義Y(t)=X(t)，R(t)=U(t)及R(t-1)=[V(t)TU(t-1)]，Y(1)=V(1)TX(1)，可得

令D(t)=R(t)S(t)，則式(6)改寫(xiě)為

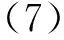
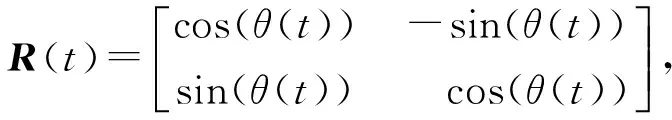
2.2RS系統(tǒng)的Ⅱ，Ⅳ象限穩(wěn)定性分析

2.2.1 Ⅱ，Ⅳ象限狀態(tài)變化 對(duì)于一個(gè)二階離散線性系統(tǒng)

在第Ⅱ象限的初始相量，當(dāng)σ1(k)gt;σ2(k),σ2(k)lt;1，σ1(k)gt;1，且π/2lt;θ(k)lt;π，初始點(diǎn)位于Ⅱ象限時(shí)，建立一個(gè)點(diǎn)經(jīng)過(guò)一次RS變換后，角度與其反向角度的差值運(yùn)動(dòng)方程為

令f(κ(k))=0，可得

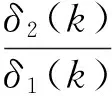
由此，特征根方程為

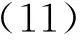
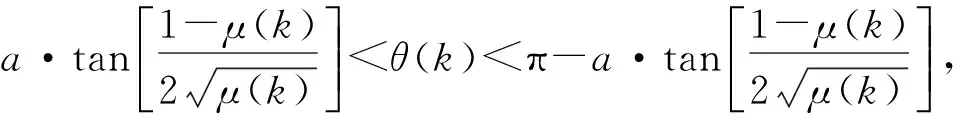
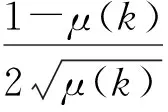
若能得斜率κ(k)經(jīng)一個(gè)R(k)S(k)變化后，斜率為κ(k+1)且位于第Ⅳ象限的(-∞，κ*(k+1))之間;而經(jīng)一次R(k+1)S(k+1)變化后，斜率為κ(k+2)且位于第Ⅱ象限的(-∞，κ1(k+2))之間，即

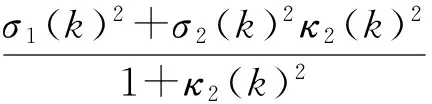
則可得該RS系統(tǒng)是不穩(wěn)定的.

3 實(shí)驗(yàn)驗(yàn)證

3.1Krawtchouk多項(xiàng)式遞歸式穩(wěn)定性分析

Krawtchouk多項(xiàng)式的三項(xiàng)遞歸迭代公式為

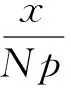
在x=390，p=0.1，0.3，0.9情況下，將Krawtchouk多項(xiàng)式整理為離散線性時(shí)變系統(tǒng)，其狀態(tài)矩陣分解為兩個(gè)旋轉(zhuǎn)矩陣和一個(gè)斜變換，經(jīng)SVD分解后可得:

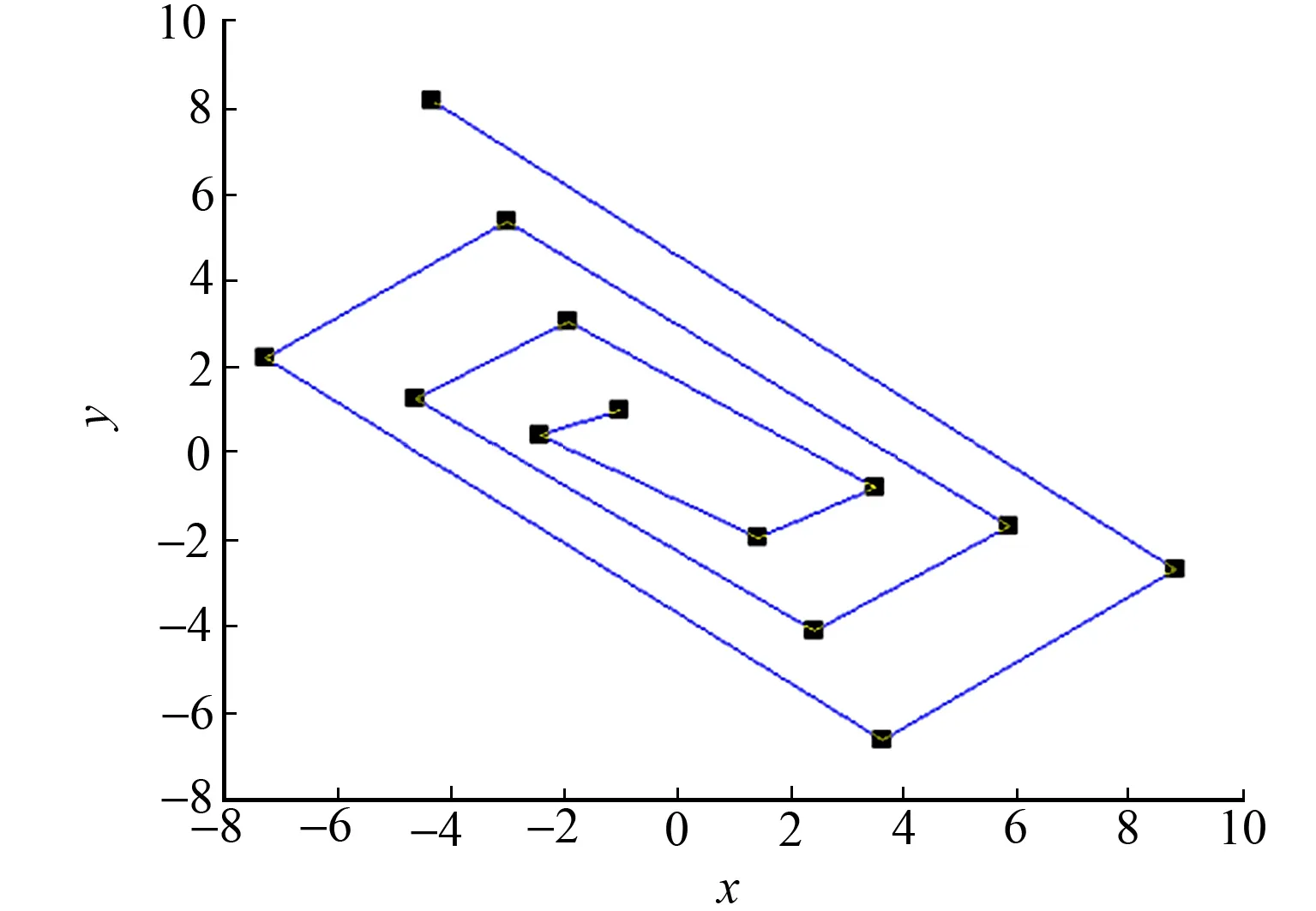
圖2 Krawtchouk的RS系統(tǒng)在Ⅱ，Ⅳ象限跳變發(fā)散情況Fig.2 RS Krawtchouk system jumps in Ⅱ,Ⅳ quadrants

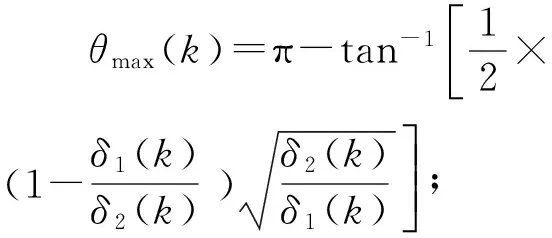
2) 對(duì)角陣S(k)的主對(duì)角線參數(shù)σ1(k)，σ2(k);

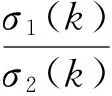
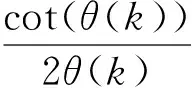
RS系統(tǒng)在Ⅱ，Ⅳ象限跳變發(fā)散，如圖2所示.各個(gè)SVD分解后的數(shù)值，如圖3所示.

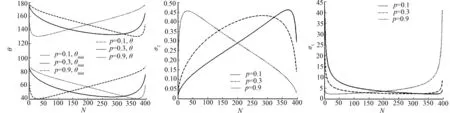
(a) θ(k)的范圍 (b) 奇異值σ2(k) (c) 奇異值σ1(k)

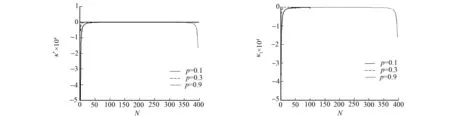
(d) κ*(k) (e) κ1(k)圖3 Krawtchouk的RS系統(tǒng)參數(shù)計(jì)算值Fig.3 Krawtchouk′s RS system parameters calculated value

3.2Jacobsthal數(shù)列遞歸式穩(wěn)定性分析

Jacobsthal數(shù)列的三項(xiàng)遞歸迭代公式為

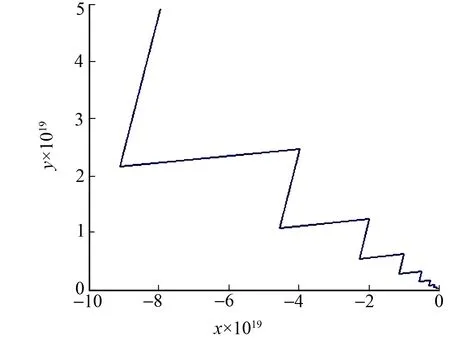
圖4 Jacobsthal的RS系統(tǒng)在Ⅱ象限跳變發(fā)散情況Fig.4 RS Jacobsthal system jumps in Ⅱ quadrant

在x=0.7，N=400的情況下，將Krawtchouk多項(xiàng)式整理為離散線性時(shí)變系統(tǒng)，其狀態(tài)矩陣分解為兩個(gè)旋轉(zhuǎn)矩陣和一個(gè)斜變換，經(jīng)SVD分解后可得

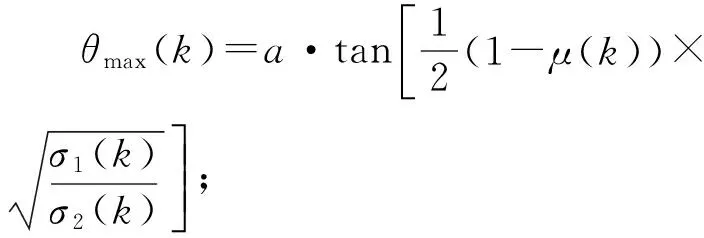
2) 對(duì)角陣S(k)的主對(duì)角線參數(shù)σ1(k)，σ2(k);

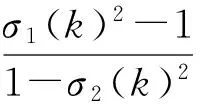
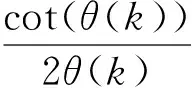
RS系統(tǒng)在Ⅱ象限發(fā)散，如圖4所示.各個(gè)SVD分解后的數(shù)值，如圖5所示.

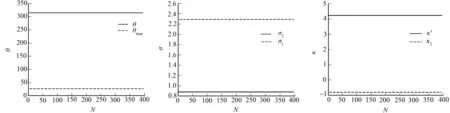
(a) θ(k)的范圍 (b) 奇異值σ1，σ2 (c) κ′(k)與κ2(k)的關(guān)系圖5 Jacobsthal的RS系統(tǒng)參數(shù)計(jì)算值Fig.5 Jacobsthal′s RS system parameters calculated value

4 Krawtchouk多項(xiàng)式圖像重構(gòu)

結(jié)合前面的實(shí)驗(yàn)分析，在x=390，p=0.1，0.3，0.9的情況下，Krawtchouk多項(xiàng)式重構(gòu)的圖像，如圖6所示.由圖6可知：當(dāng)p=0.1時(shí)，Krawtchouk多項(xiàng)式的遞歸計(jì)算誤差已經(jīng)增大，只能重構(gòu)圖像的部分；當(dāng)p=0.3時(shí)，誤差依舊很大，導(dǎo)致也只能重構(gòu)部分的圖像；當(dāng)p=0.5時(shí)，Krawtchouk多項(xiàng)式遞歸計(jì)算的誤差慢慢減小，重構(gòu)的效果慢慢變好；隨著階數(shù)的增加，當(dāng)p=0.9時(shí)，重構(gòu)圖像效果與p=0.1和p=0.3的圖基本一樣.

(a) p=0.1

(b) p=0.3

(c) p=0.5圖6 不同p值的Krawtchouk多項(xiàng)式圖像重構(gòu)Fig.6 Image reconstruction of Krawtchouk polynomials with different p values

圖7 Krawtchouk峰值信噪比Fig.7 Krawtchouk peak signal to noise ratio

根據(jù)圖像評(píng)價(jià)標(biāo)準(zhǔn)，分別作出Krawtchouk的p值(Kp)為0.1，0.3，0.5的峰值信噪比(RPSN=10·log(2552/MSE)，MSE為均方差)，其值越高說(shuō)明重構(gòu)圖像效果越好，如圖7所示.由圖7可知：Krawtchouk多項(xiàng)式的峰值信噪比隨著階數(shù)的增加而增加，到一定程度時(shí)，其值迅速下降.說(shuō)明高階的時(shí)候其誤差是變大的導(dǎo)致其發(fā)散,驗(yàn)證了Krawtchouk正交多項(xiàng)式在Ⅱ,Ⅳ象限發(fā)散的情況.

5 結(jié)束語(yǔ)

分析和研究離散時(shí)變線性系統(tǒng)，將系統(tǒng)的狀態(tài)矩陣進(jìn)行奇異值分解，得到新的等效狀態(tài)方程.通過(guò)分析Krawtchouk正交多項(xiàng)式與Jacobsthal數(shù)列遞歸式，計(jì)算時(shí)，通過(guò)不同的判據(jù)，說(shuō)明了Krawtchouk矩陣在Ⅱ,Ⅳ象限跳變的原因，也說(shuō)明了Jacobsthal數(shù)列在第Ⅱ象限發(fā)散的原因.所進(jìn)行的只是初步討論了Ⅱ,Ⅳ象限的情況，其他象限情況還有待進(jìn)一步研究.

[1] 王宏偉，趙國(guó)慶.遞歸算法的參數(shù)設(shè)置[J].電波科學(xué)學(xué)報(bào)，2010，25(6):1187-1192,1234.

[2] 鞠憲龍.二階對(duì)角遞歸神經(jīng)網(wǎng)絡(luò)的算法研究及應(yīng)用[D].哈爾濱:哈爾濱工程大學(xué)，2011.

[3] 趙堅(jiān).一般二階線性常系數(shù)齊次遞歸方程在數(shù)論中的應(yīng)用[J].哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2000，32(6):132-135.

[4] YAP P T，PARMMESRAN R，ONG S H.Image analysis by Krawtchouk moments[J].IEEE Transactions on Image Processing，2003，12(11):1367-1377.

[5] 龍愛(ài)芳，胡軍浩.基于Hermite插值的高精度數(shù)值積分公式[J].華僑大學(xué)學(xué)報(bào)(自然科學(xué)版)，2013，34(3):349-352.DOI:10.11830/ISSN.1000-5013.2013.03.0349.

[6] 田萌，王文劍.基于正交多項(xiàng)式的核函數(shù)性質(zhì)研究[J].模式識(shí)別與人工能，2014，27(5):385-393.

[7] 李炳坤.切比雪夫逼近多項(xiàng)式在非線性電路中的應(yīng)用[J].華僑大學(xué)學(xué)報(bào)(自然科學(xué)版)，1992，13(4):558-562.DOI:10.11830/ISSN.1000-5013.1992.04.0558.

[8] 宮鳳強(qiáng)，李夕兵.基于Legendre正交多項(xiàng)式逼近法的結(jié)構(gòu)可靠性分析[J].工程力學(xué)，2008，25(6):225-229.

[9] MUKUNDAN R，ONG S H，LEE P A.Image analysis by tchebichef moments[J].IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society，2001，10(9):1357-1364.DOI:10.1109/83.941859.

[10] GAUTSCHI W.Computational aspects of three-term recurrence relations[J].Siam Review，1967，9(1):24-82.

[11] GAUTSCHI W.Is the recurrence relation for orthogonal polynomials always stable?[J].BIT，1993，33(2):277-284.DOI:10.1007/BF01989750.

[12] 關(guān)軼峰，李鐵壽.二階離散線性時(shí)變系統(tǒng)的一種穩(wěn)定性判據(jù)[J].計(jì)算技術(shù)與自動(dòng)化，2003，22(4):12-15.

[13] MUKUNDAN R.A comparative analysis of radial-tchebichef moments and zernike moments[C]∥Procedings of the British Machine Vision Conference.London:BMVA Press,2009:16(1-7).DOI:10.5244/C.23.16.

[14] 張海艷，高尚兵.圖像分割中改進(jìn)空間約束貝葉斯網(wǎng)絡(luò)模型的應(yīng)用[J].計(jì)算機(jī)應(yīng)用，2017，37(3):823-826,831.DOI:10.11772/j.issn.1001-9081.2017.03.823.

(責(zé)任編輯： 陳志賢英文審校： 吳逢鐵)

NumericalStabilityMethodofSecondOrderRecursiveSystemUsingSingularValueDecomposition

FU Bo， LIU Jiyuan， ZHAO Xilin， XU Guanghui, WANG Zipeng

(School of Electrical and Electronic Engineering， Hubei University of Technology， Wuhan 430068， China)

In order to solve the problem of stability of second order recursive systemsimply， the second order recursive system is transformed into second order discrete time-varying linear system and the stability of recursive system is discussed. Based on the stability analysis of second-order discrete linear time-varying systems， converting it into a reference signal (RS) system by singular value decomposition (SVD). Based on discrete orthogonal Krawtchouk polynomials and the Jacobsthal series, a new sufficient condition for discrete time-varying linear instability is proposed. The changes and new instability codes in the second and fourth quadrants are discussed and deduced. The simulation results verify the conclusion accuracy.

Krawtchouk polynomials; Jacobsthal sequences; singular value decomposition; recursive systems; linear discrete time-varying systems

10.11830/ISSN.1000-5013.201703080

TP 391

A

1000-5013(2017)06-0886-06

2017-03-30

付波(1973-)，男，教授，博士，主要從事圖像處理與模式識(shí)別的研究.E-mail:fubofanxx@mail.hbut.edu.cn.

國(guó)家自然科學(xué)基金資助項(xiàng)目(61072130， 51309094， 61603127)； 國(guó)家教育部留學(xué)回國(guó)人員科研啟動(dòng)基金資助項(xiàng)目(20141685)； 湖北省科技廳重大科技專(zhuān)項(xiàng)項(xiàng)目(2013AE001)