木結構古建筑抗震性能參數分析

張錫成，馬赫迪，代武強，吳晨偉

（西安建筑科技大學 土木工程學院，陜西 西安710055）

木結構古建筑抗震性能參數分析

張錫成，馬赫迪，代武強，吳晨偉

（西安建筑科技大學 土木工程學院，陜西 西安710055）

不同構造形式及其參數取值對木結構古建筑的動力特性及抗震性能有直接影響，因此研究參數變化對結構動力性能的影響規律，對于木結構古建筑的修繕與加固保護具有重要的指導意義。基于宋代《營造法式》制作了某單層單開間殿堂式木結構模型，建立了考慮柱礎滑移隔震、榫卯半剛性連接及斗栱減震性能的空間桿系有限元模型，并與單向水平地震激勵下的振動臺試驗進行了對比；通過參數分析探索了木結構斗栱、榫卯及屋蓋等不同構造方式及相應結構參數取值的改變對其抗震性能的影響。結果表明：隨著斗栱剛度的增大，整體結構的自振頻率收斂于上限2.08 Hz，且其耗能減震作用逐漸變弱；隨著榫卯節點的剛度逐漸變大，整體結構的自振頻率收斂于上限3.26 Hz，柱腳的滑移量會隨之增大而柱架側移卻隨之減小，而榫卯節點剛度的減小在減少柱腳滑移量的同時會使得柱架的側移變形大大增加，榫卯節點的剛度變化對結構自振頻率的影響程度大于斗栱剛度；屋蓋質量的增加會降低結構的自振頻率，增大斗栱的水平變形，提高整體結構的抗震能力。

木結構古建筑；桿系模型；構造方式；抗震能力

0 引言

木結構建筑歷史悠久，其豐富的科學和文化價值是中國乃至世界不可多得的瑰寶。近年來，許多學者通過試驗和理論分析的方法對古建筑木結構的結構性能及抗震機理展開了大量科學研究，并取得了一系列的學術成果。謝啟芳等通過對榫卯節點的抗震性能研究，建立了榫卯連接的恢復力模型［1-2］，并對斗栱力學性能進行了試驗研究，得到了其荷載—位移滯回曲線［3］。高大峰等通過試驗得到斗栱在豎向荷載作用下的力—位移關系曲線［4］。Fang等通過對西安北門箭樓木構架進行現場測試與理論分析，對其動力特性進行了研究［5-6］。周乾等以故宮太和殿為研究對象，通過對古建筑的榫卯節點、斗栱等構造特征進行數值模擬，分析了其抗震性能［7-9］。日本學者對日式傳統木結構建筑進行了大量試驗分析，對柱與礎石的連接性能［10］、榫卯節點的半剛性性能［11］、斗栱的力學性能［12］及整體結構的抗震性能［13］進行了系統研究。

目前的研究主要針對某一特定的結構構件或者具體建筑進行分析，而不同構造形式及相關參數對木結構動力特性的影響規律方面研究較少。因此，在現有研究成果的基礎上，通過對殿堂式木結構古建筑的有限元建模及參數分析，對斗栱、榫卯及屋蓋等不同構造形式及其參數取值對其動力特性的影響，研究各參數變化對古建筑木結構抗震性能的影響規律，以期為木結構古建筑的修葺與加固保護提供理論依據。

1 木結構有限元分析模型的構建

1.1 簡化分析模型

參照宋代《營造法式》制作了某單層單開間殿堂式木結構模型［14］，其模型構造形式及構件尺寸如圖1所示。采用桿系單元與彈簧單元的組合形式建立殿堂結構計算模型如圖2所示，其中各單元的選取原則為

圖1 模型及構件尺寸圖／mm

（1）柱、額枋及梁單元的選取

通常采用BEAM188梁單元處理線性、大角度轉動及非線性大應變等問題，故柱、額枋及梁等構件的力學行為可用此單元來模擬。木材的正交各向異性可通過材性試驗的實測數據來反映，采用該單元沿3個方向的彈性模量及泊松比來描述。

（2）柱與額枋的榫卯連接

在木結構古建筑中，柱與額枋之間的榫卯連接節點介于鉸接與剛接之間，具有半剛性的特點。因此，節點在傳遞軸力、剪力、扭矩及彎矩作用的同時，又會產生一定的變形。其中，節點在受到彎矩作用所產生的轉動變形為主要變形，其軸向拉壓變形、剪切變形及扭轉變形可以不予考慮，故采用彎矩—轉角曲線榫卯節點的力學特性描述。因此，用類似于榫卯節點連接的非線性彈簧來進行有限元分析，以此達到簡化分析的目的，在此采用COMBIN39彈簧單元來模擬榫卯節點的半剛性性能。

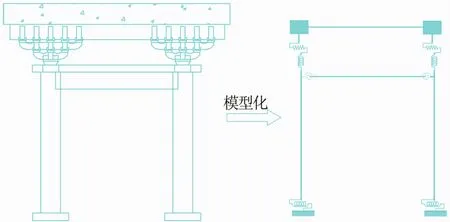
圖2 殿堂結構的計算簡圖

（3）柱與礎石的連接

在木結構古建筑的柱與礎石之間，只能通過摩擦力來平衡水平荷載。當礎石的最大靜摩擦力大于水平荷載時，柱與礎石之間類似于鉸接連接，只發生轉動變形；而當礎石的最大靜摩擦力小于水平荷載時，相對滑移就會產生。因此，柱與礎石間的滑動摩擦力就是結構底部所能抵抗的最大水平剪力。這種情況下，在柱底加上一個虛擬的水平彈簧單元。當柱與礎石之間的最大靜摩擦力大于水平剪力時，此單元沒有變形產生，此時彈簧剛度K為無窮大，而當最大靜摩擦力小于水平剪力時，彈簧的內力不改變，且為最大靜摩擦力，此時彈簧對柱腳不產生約束，即此時的K為零。因此，對滑移連接特性的模擬可以通過在柱腳與礎石之間采用COMBIN40單元來完成。

（4）斗栱

在水平地震作用時，斗栱所要承受的力主要來自于上部屋蓋梁架的自重及其傳遞的水平剪力。在通過力—變形曲線來描述斗栱力學特性時，可以采用水平及豎直2個方向的平動彈簧簡化斗栱。水平彈簧單元可以用COMBIN14單元來模擬，斗栱在軸向壓力作用下的力學性能可以通過把該單元設置為一維軸向彈簧—阻尼器來模擬，豎向彈簧單元則選擇COMBIN39單元來模擬斗栱在水平力作用下的非線性特性。可以由四朵斗栱平均分擔屋蓋梁架系統的自重，且分擔的質量集中作用在其頂部。通過以上分析，殿堂結構一榀平面構架的計算圖如圖2所示，柱底取至礎石頂面，采用柱、額枋及乳栿的形心線作為各自的軸線，所示的彈簧單元幾何尺寸都為零。空間模型也可按照上述的簡化分析推廣得到。

1.2 單元實常數的確定

（1）平動彈簧單元實常數

在相同條件的水平荷載作用下，通過低周反復荷載試驗對振動臺試驗模型中的單朵斗栱進行分析［15］，得到了其恢復力特性，如圖 3（a）所示。同時對振動臺試驗模型進行試驗［4］，得到單朵斗栱在豎向荷載作用下的力學行為，如圖3（b）所示。

對COMBIN39彈簧單元的實常數的定義可以根據圖3（a）所示的水平力—側移曲線確定。設置KEYOPT（1）＝1，即按照ANSYS內置的卸載準則定義COMBIN39彈簧單元的滯回規則符。卸載路徑的卸載方向選擇沿通過原點且平行的線段進行。

豎向力與豎向位移之間可近似看作線性關系，由圖3（b）所示的豎向力—側移曲線可得到。然后賦予COMBIN14單元實測得到的豎向剛度值，將試驗數據進行線性擬合，COMBIN14單元的實常數項可選用得到的單朵斗栱的豎向剛度K為6 kN／mm，用此彈簧常數來進行斗栱的軸向性能的模擬。

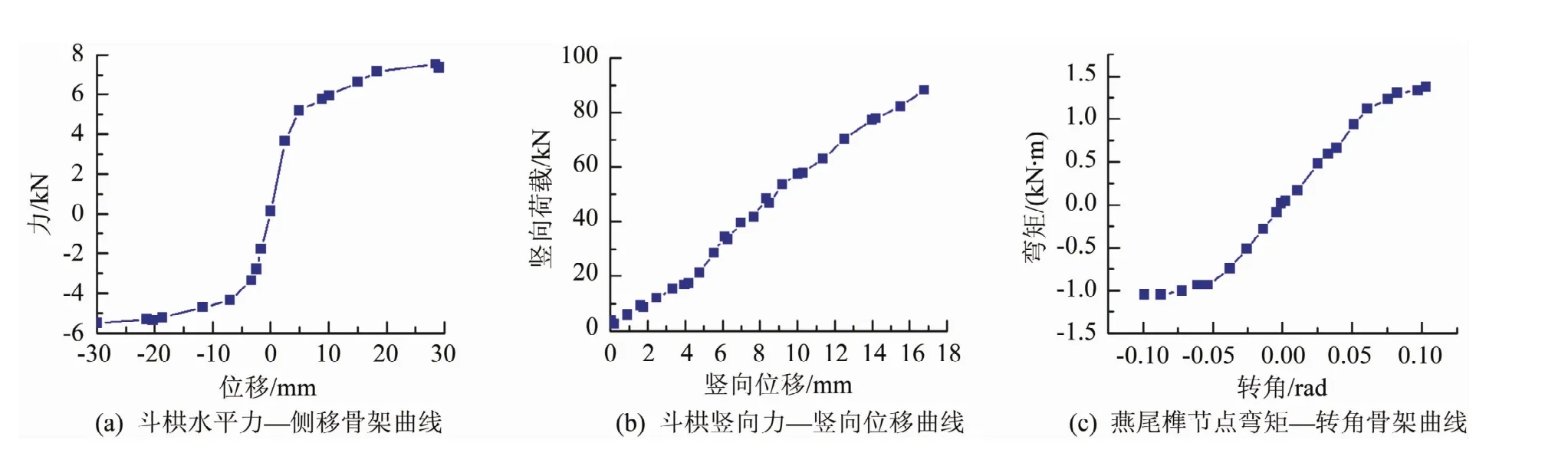
圖3 單元實常數確定圖

（2）COMBIN39轉動彈簧單元實常數

在水平荷載作用下，進行單榀柱架的低周反復荷載試驗［15］。對榫卯節點的恢復力特性進行分析，得到節點彎矩—轉角關系曲線，如圖3（c）所示。根據此曲線可以定義COMBIN39彈簧單元的實常數。同樣，按照ANSYS內置的卸載準則定義該單元的滯回規則，即設置KEYOPT（1）＝1。卸載路徑選擇沿過原點且與其平行的線段方向。

（3）COMBIN40單元實常數

制作了6組紅松柱段與青石石板對靜摩擦系數進行測定［14］。其所采用的是與振動臺試驗模型相同的材料、尺寸和制作工藝。紅松與青石板之間的靜摩擦系數經過試驗測定其平均值μ為0.33。在簡化計算模型當中，可以取單個柱所能承受的最大靜摩擦力作為COMBIN40單元的臨界滑動力，同時令滑動彈簧水平剛度K1為∞，彈簧二階剛度K2為0，空隙GAP為0。

1.3 有限元模型的建立

在對結構的有限元分析模型進行參數化編程時，計算模型直接由ANSYS內置的APDL語言生成。柱腳與礎石之間的滑移連接通過在柱腳位置處添加COMBIN40單元來模擬。在與柱腳節點重合的位置，額外生成4個節點，作為地面節點，對UX、UY、UZ、ROTX、ROTY、ROTZ 6個方向的自由度進行約束，4個柱腳節點在UZ、ROTZ等2個方向的自由度也同樣被約束。柱腳摩擦滑移單元采用沿x、y向的COMBIN40單元分別將地面節點及柱腳節點進行連接形成。屋蓋的質量通過在4個乳栿相交的節點處添加Mass21單元來模擬。因其轉動慣性可忽略，故將其設置為2D單元。所建立的有限元模型如圖4所示，KO和MO分別表示彈簧單元和質量單元。

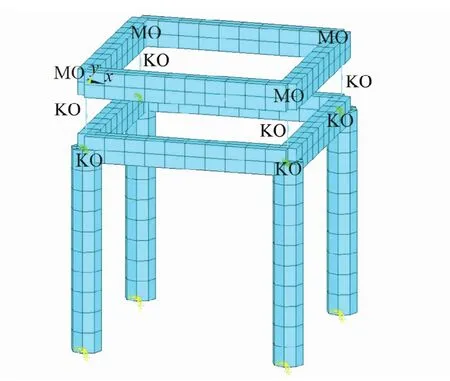
圖4 有限元計算模型圖

1.4 地震模擬計算結果與驗證

在對結構進行不同工況下的加速度地震波的瞬態動力分析后，將不同節點的計算結果采用ANSYS程序提取出來。由于只在一個方向輸入地震波，且有限元計算模型的結構布置均勻對稱，因此，不考慮結構扭轉，標高相同處的加速度在水平方向上也大致相等，所以代表柱腳、柱架頂面及屋蓋的測點可任意在柱底、柱頂及乳栿端的節點中進行選擇。為驗證所選取的有限元模型的準確性，通過對屋蓋加速度以及相對位移反應進行研究分析，將所得到的計算結果與振動臺試驗結果［10］進行對比，如圖5所示。

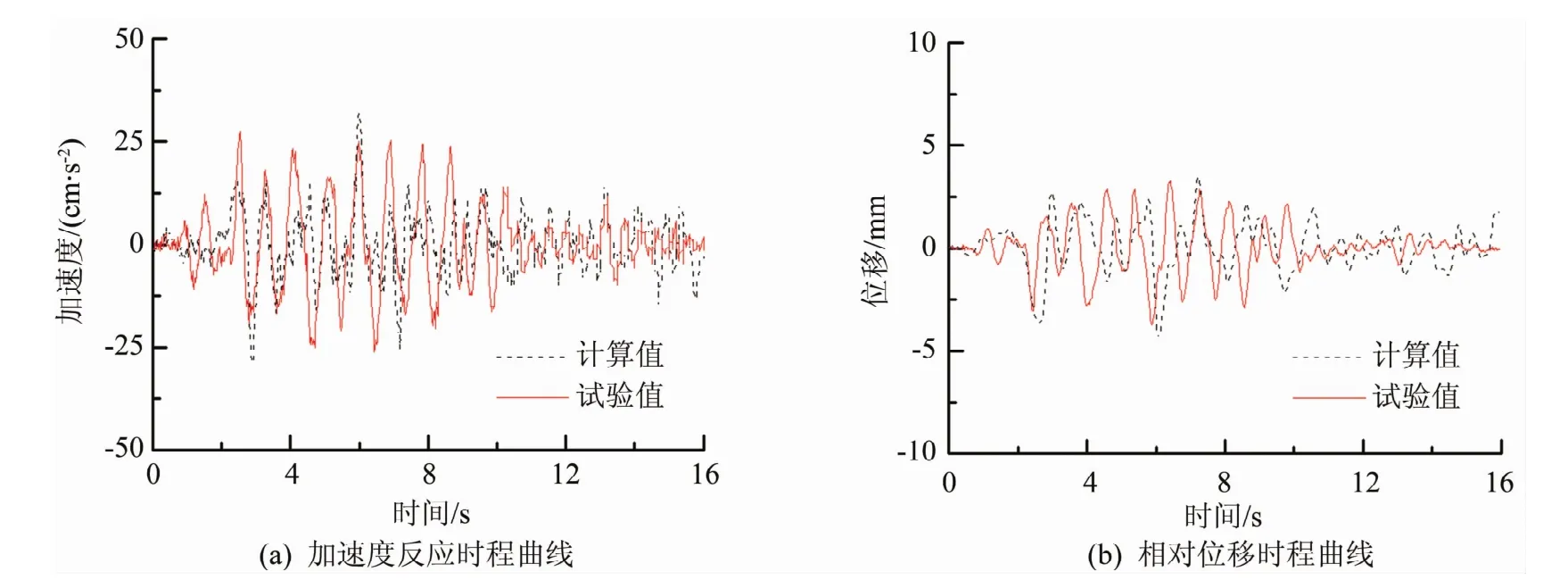
圖5 蘭州-50工況屋蓋加速度及相對位移反應的計算值與試驗值對比圖

由圖5分析可知，屋蓋加速度反應和相對位移反應時程曲線的計算值與試驗值吻合程度較高，到達峰值時刻也基本相同，說明所建立的模型單元一定程度上可以很好的模擬真實情況。

2 抗震性能主要參數分析

結合目前的研究成果［16］并考慮到影響古建筑木結構動力特性的因素，選取斗栱剛度kd、榫卯節點剛度kj及屋蓋的質量m等主要參數，分別探討斗栱、榫卯及屋蓋不同構造方式的影響。通過修改空間桿系有限元模型的相關參數，對其進行拓展參數分析。

2.1 斗栱剛度

2.1.1 斗栱剛度與自振頻率關系分析

設計算模型中斗栱的剛度為kd，原始結構中斗栱的初始剛度為kd0，則尺寸構造不同的斗栱可以用二者比值大小的變化來模擬，計算模型在不同斗栱剛度下的自振頻率及周期見表1，并將表1中數據繪于圖6。

表1 計算模型在斗栱剛度變化下的自振頻率及周期

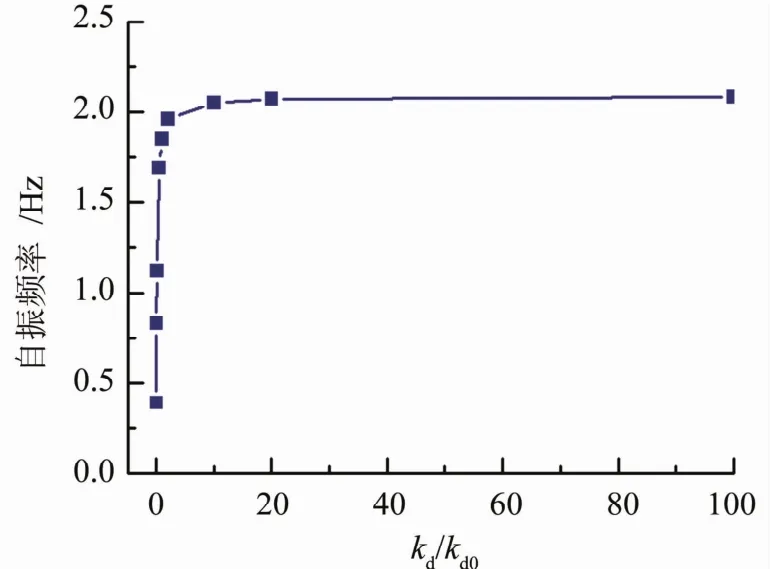
圖6 斗栱剛度變化下計算模型的自振頻率圖

從圖6可以看出，整個結構的自振頻率明顯受到斗栱剛度的影響。當kd／kd0＜10時，結構自振頻率隨著斗栱剛度的增大，增幅明顯較快；當kd／kd0＞20時，結構的自振頻率增幅放緩，最后自振頻率收斂于上限 2.08 Hz。

2.1.2 斗栱剛度對抗震性能的影響

通過輸入El Centro波300 cm／s2，并不斷調整斗栱的剛度比值，對模型進行動力時程分析。不同剛度比值情況下試驗得到的結構反應見表2。

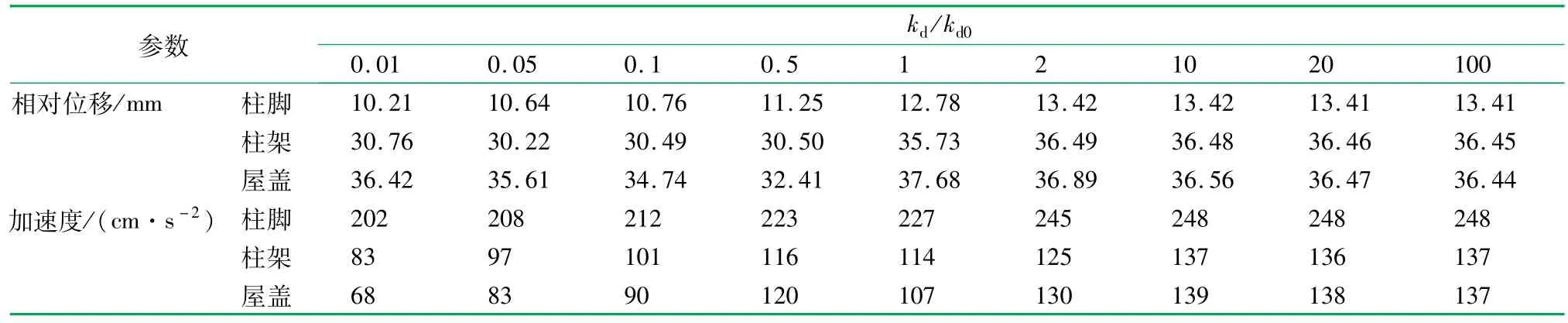
表2 計算模型在斗栱剛度變化下各位置處的最大地震反應

由表2可看出，結構的地震反應直接受到斗栱剛度大小變化的影響。由圖7可知，隨著斗栱剛度的增加，柱腳、柱架及屋蓋處的最大相對位移反應和最大加速度反應都明顯增大，相反，斗栱的側移變形卻在減小。這是因為kd／kd0的增加使得結構的整體抗側剛度提高，柱架及屋蓋等上部結構的加速度反應因此而加大，導致結構的層間剪力變大。但由于kd／kd0的提高幅度遠遠大于層間剪力的增幅，所以斗栱的側移變形才減小。

可用屋蓋處與柱架頂面的動力放大系數來衡量斗栱的耗能減震作用效果。從圖7（d）中可看出，隨著kd／kd0的增加，動力放大系數在初期急劇上升，隨后趨于穩定，并最終趨近于1。這說明，較小的斗栱剛度在耗能減震作用有著較好的表現。斗栱的耗能減震作用在其剛度不斷增加時，逐漸減弱，直至屋蓋的加速度與柱架頂面的加速度相同，此時斗栱的作用類似于剛體，側移趨近于0，如圖7（c）所示。因此，斗栱的剛度大小決定著斗栱耗能減震性能的強弱。斗栱剛度越小，其具備的變形性能越好，抗震時性能就發揮的越充分。

2.2 榫卯節點剛度

2.2.1 榫卯節點剛度與自振頻率關系分析

設榫卯節點在計算模型中的抗彎剛度為kj，對應于原始結構的初始剛度為kj0，不同的榫卯連接方式可以通過調整二者比值的大小來模擬。表3給出了計算模型在榫卯連接剛度變化時的自振頻率及周期。表3中，榫卯節點在kj／kj0＝∞時表現為剛性，而當kj／kj0＝0時，結構為可變體系，故可以不考慮此情況。將表3中數據繪于圖8。

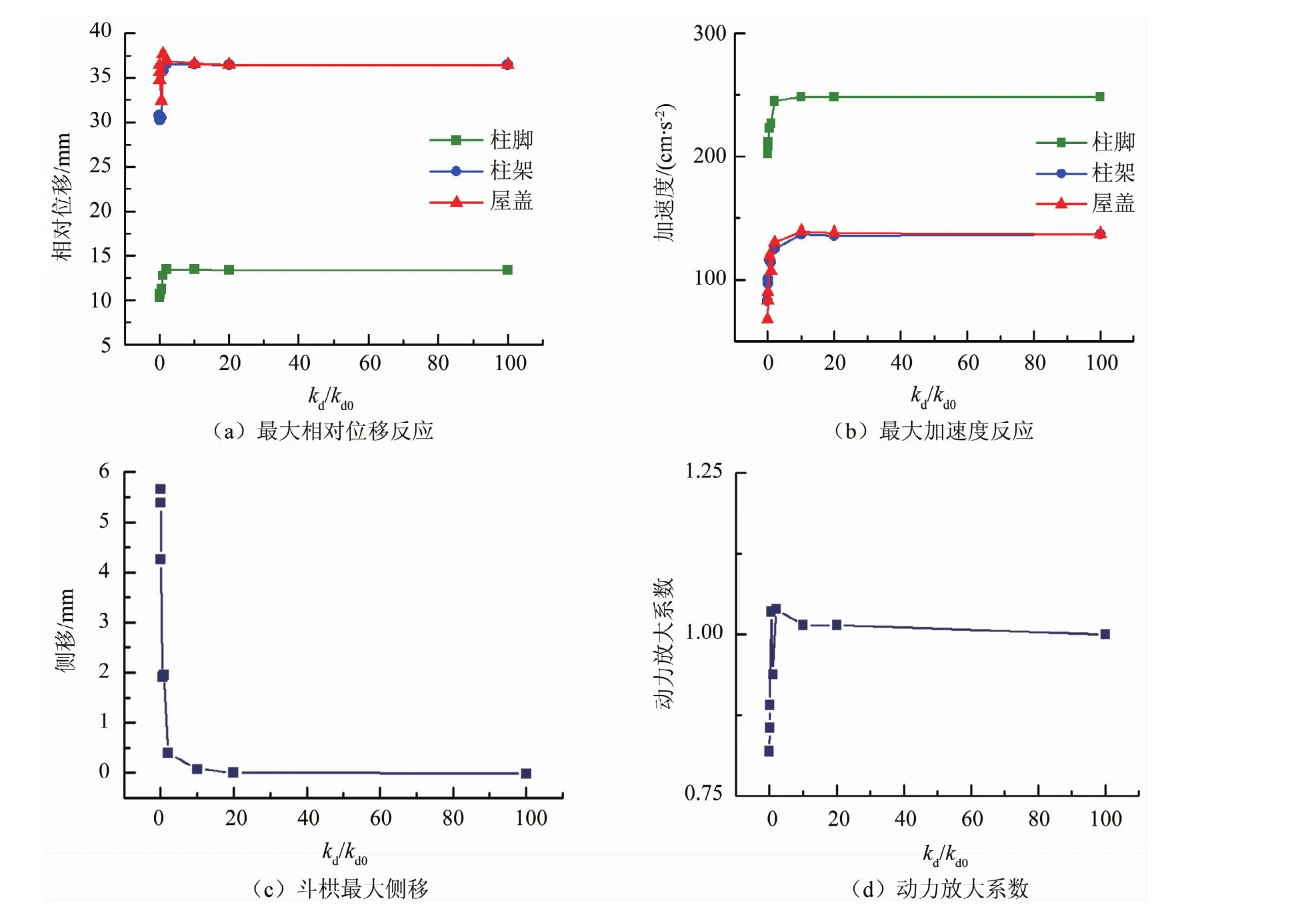
圖7 斗栱剛度比變化下結構的最大地震反應及動力放大系數圖

表3 計算模型在榫卯連接剛度變化下的自振頻率及周期表

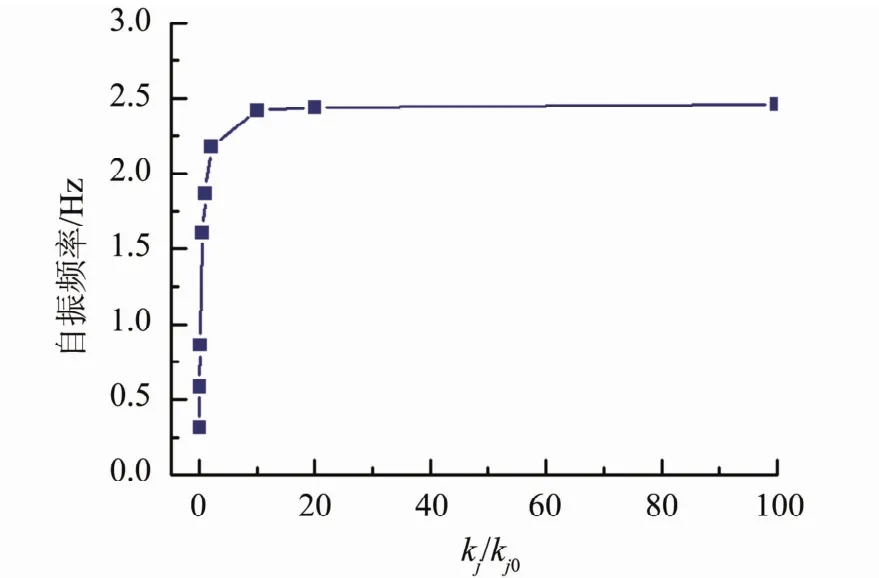
圖8 榫卯連接剛度變化下計算模型的自振頻率圖

由以上數據可以看出，整個結構的自振頻率與榫卯節點的剛度大小之間有著直接影響。當kj／kj0＜10時，結果的自振頻率隨著節點剛度的增大，增幅明顯較快；當kj／kj0＞20時，結構的自振頻率增幅放緩，最后收斂于上限3.26 Hz，此時，結構的自振頻率就為節點剛接時結構的最大自振頻率。結構自振頻率在榫卯節點剛度變化時，所產生的影響較斗栱剛度對結構產生的影響更加明顯。從表3可以看出，由榫卯節點剛度變化引起的頻率波動范圍為0.31～3.26 Hz，而斗栱剛度的變化在相同的剛度比值下所導致結構的自振頻率波動范圍僅為0.39～2.08 Hz。榫卯節點的剛度變化對結構自振頻率的影響程度大于斗栱剛度的影響，榫卯節點剛度的大小對整體結構自振頻率的高低起決定性作用。

2.2.2 榫卯節點剛度對抗震性能的影響

通過輸入El Centro波300 cm／s2，并不斷調整榫卯節點剛度的大小，對模型進行動力時程分析，得到的剛度比值情況變化下的最大結構反應見表4。

從表4可以看出，結構的地震反應直接受到榫卯連接剛度大小的影響。由圖9可以看出，在相對位移反應方面，柱腳的滑移量隨著節點剛度的增加而不斷增大，而柱架的側移變形卻隨之減小。這是因為柱架的整體抗側剛度隨著kj／kj0的增加而提高，使得結構的抗側移變形能力增強，在減小柱架的側向變形減小的同時，也造成了上部結構的加速度反應的增大，如圖10所示。此時結構底部剪力也會因 此而變大，進而表現為柱腳的滑移量增大。

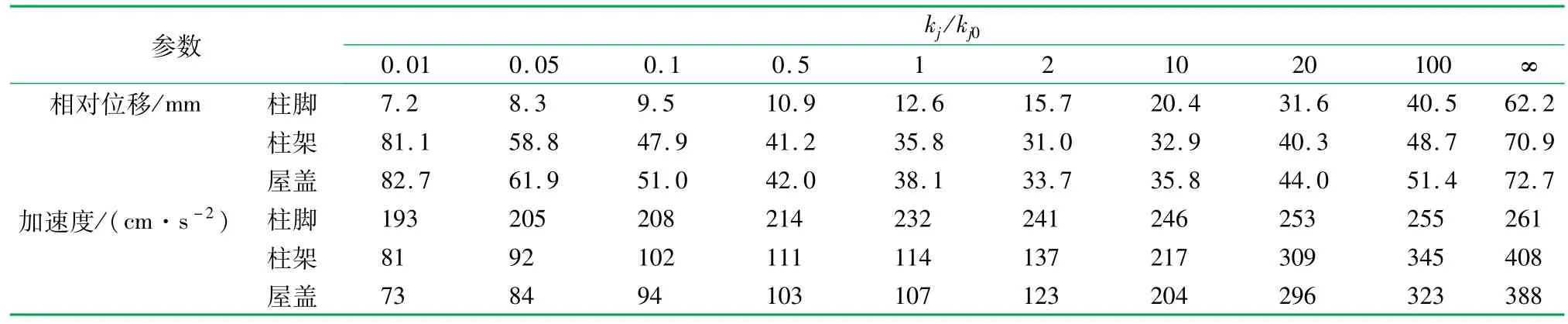
表4 計算模型在榫卯連接剛度變化下各位置處的最大地震反應

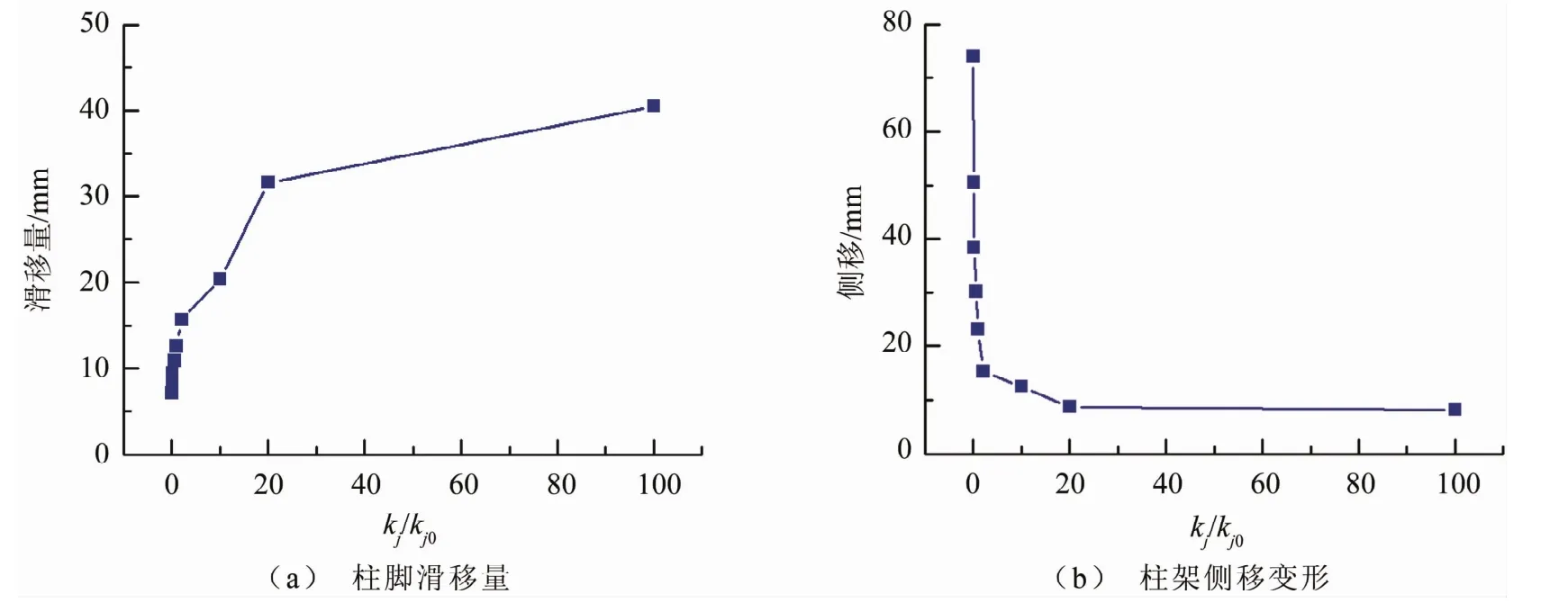
圖9 節點剛度變化下的最大柱腳滑移量及最大柱架側移變形圖

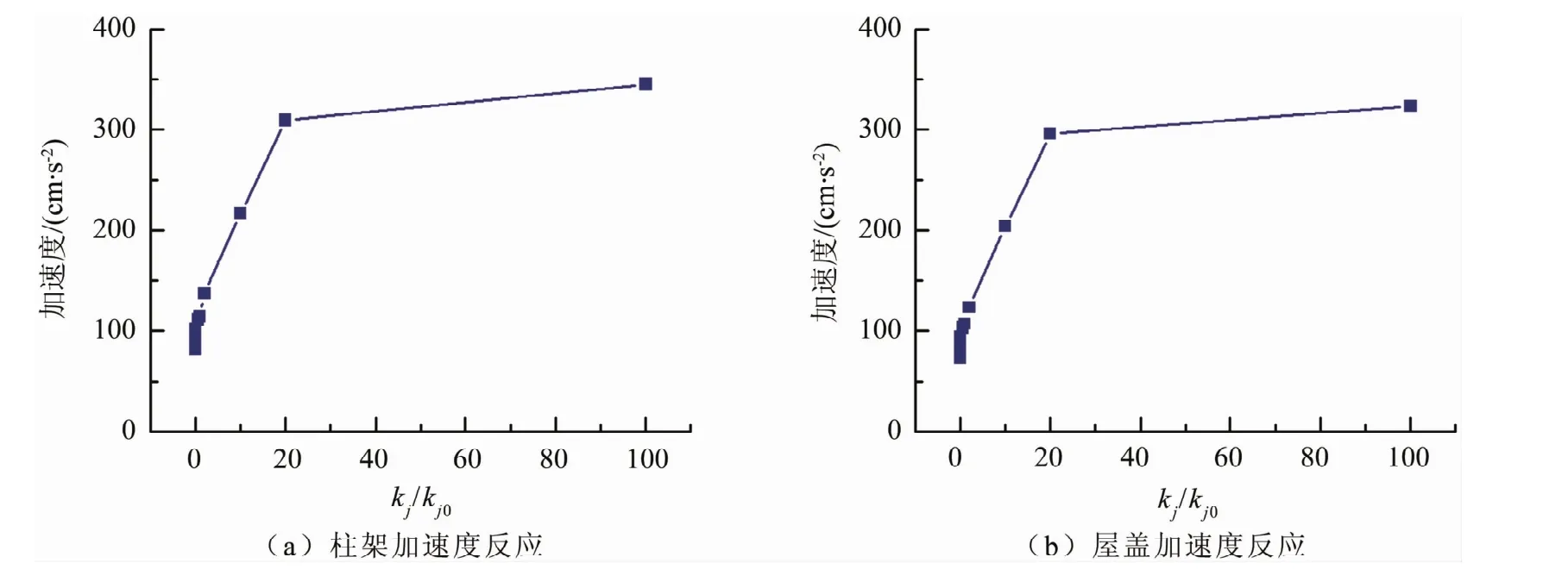
圖10 節點剛度變化下的各位置處的最大加速度反應圖

由上述分析可知，榫卯節點處于木結構古建筑抗震減震體系中的關鍵地位，同時也是比較脆弱的部分。榫卯節點的剛度大小直接影響結構的抗震能力，節點剛度的增加使柱腳滑移量增大，柱腳容易滑出柱礎造成結構落架倒塌；其剛度的減小則會使柱架的側移變形增大，同樣會導致結構發生倒塌破壞。所以，在進行木結構古建筑修繕加固時，應給出加固后合理的榫卯節點剛度區間，在保證柱架、屋蓋處的相對位移和加速度反應處在允許范圍內的同時，相應的柱腳滑移量不至于過大而導致結構倒塌。

2.3 屋蓋質量

2.3.1 屋蓋質量與自振頻率關系分析

設計算模型中屋蓋質量為m，原始結構中屋蓋的質量為m0，不同形制構造的屋蓋可用二者比值的大小來模擬。計算模型在屋蓋質量變化時的自振頻率及周期如圖11所示。

由圖11可以得知，結構的自振頻率直接受到屋蓋質量大小的影響。結構的自振頻率在屋蓋質量的增大的同時，隨之降低。根據結構基本頻率的計算公式也可以得到同樣的結論，結構質量在剛度一定時，與基本頻率成反比。結構的自振頻率在結構質量無限大時，無限接近于0。

2.3.2 屋蓋質量對抗震性能的影響

El Centro—300工況下屋蓋質量比值情況變化下的最大結構反應見表5。

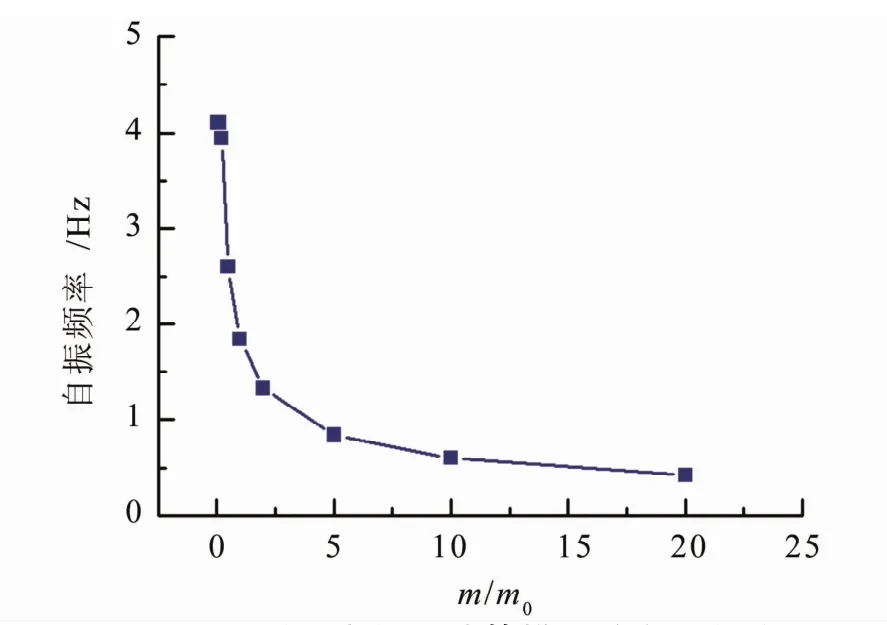
圖11 屋蓋質量變化時計算模型的自振頻率圖

由表5和圖12可以看出，隨著屋蓋質量的增加，結構各位置處的加速度反應都在減小，而對應的相對位移反應卻在增大。這是由于屋蓋質量的增加延長了整體結構的自振周期，使之錯開地震波的卓越周期。因此，增大了與輸入激勵的頻率兩者之間的比值，結構的加速度反應因此而減小。但是盡管如此，結構所受的地震慣性力由于屋蓋質量的大大增加依然很大，這就使得結構各部分的剪力也同樣很大，導致了各位置的層間變形的增大，如圖13所示。

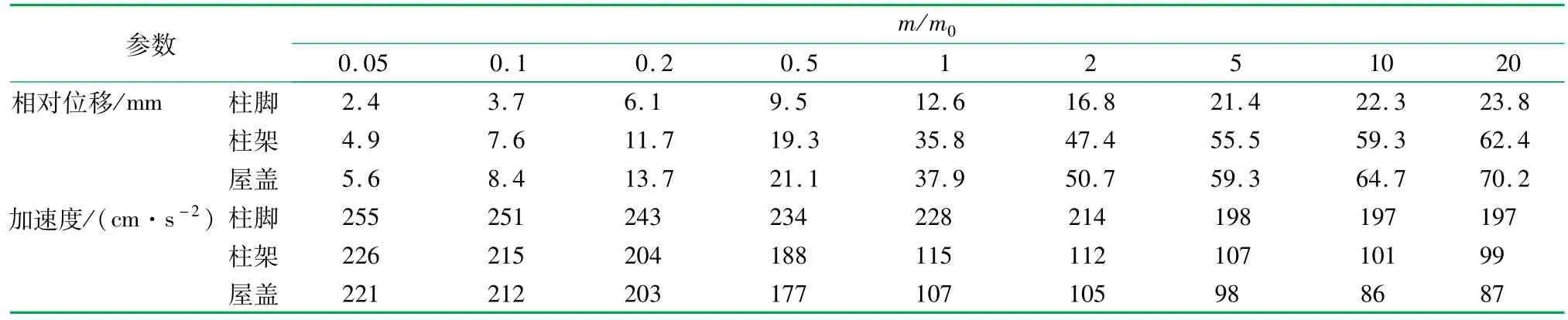
表5 屋蓋質量變化下計算模型各位置處的最大地震反應

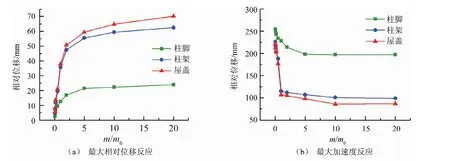
圖12 屋蓋質量比變化時的最大結構地震反應圖

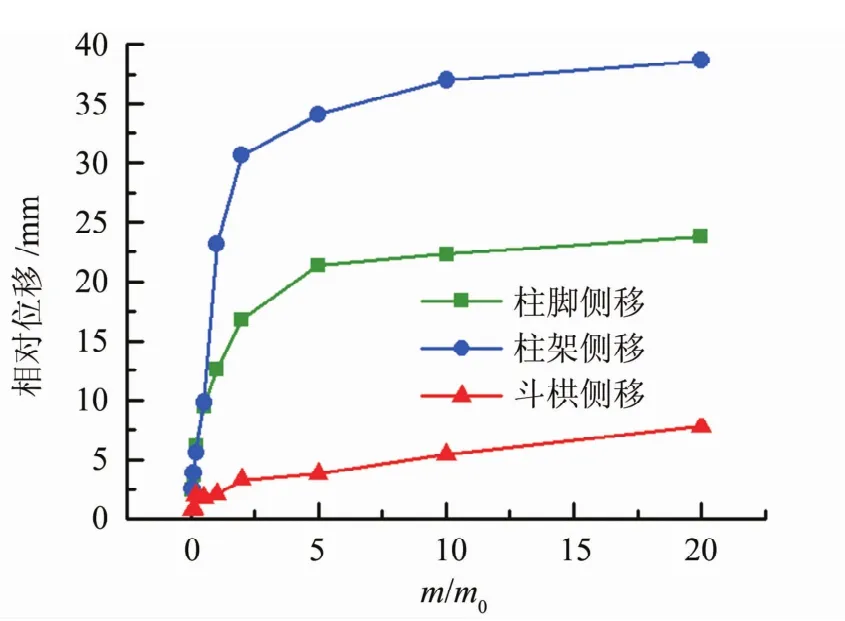
圖13 屋蓋質量比變化時各位置的最大側移圖

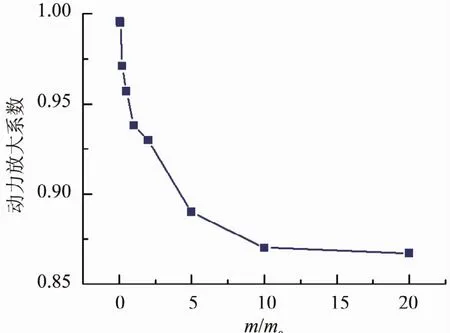
圖14 動力放大系數圖

分析斗栱的耗能減震作用所受到屋蓋質量影響時，可通過衡量屋蓋處與柱架頂面處最大加速度反應的動力放大系數來分析，如圖14所示。斗栱在屋蓋質量較小時，所受到屋蓋傳下來的剪力非常小，動力放大系數接近1，基本沒有變形產生，因此斗栱沒有發揮耗能減震能力。斗栱在屋蓋質量的增加的同時，產生的水平變形也在增大，而同時，加速度動力放大系數減小，說明斗栱的耗能減震作用逐漸增強。

3 結論

通過上述研究表明：

（1）斗栱剛度的增加引起結構自振頻率的增大，自振頻率的增幅在kd／kd0＜10時較快，在 kd／kd0＞20時收斂于上限2.08 Hz；同時還使結構各位置相對位移和加速度反應增大，斗栱的側移減少，說明斗栱減震耗能的作用隨著其剛度的增加而減弱。

（2）榫卯節點剛度的增加引起結構自振頻率的增大，自振頻率增幅在 kj／kj0＜10時較快，在kj／kj0＞20時，收斂于上限 3.26 Hz；榫卯節點剛度的增加會造成柱腳的滑移量的增大以及柱架側移的減小，而榫卯節點剛度的減小在減少柱腳滑移量的同時，使得柱架的側移變形大大增加。榫卯節點的剛度變化對結構自振頻率的影響程度大于斗栱剛度對其的程度，因此榫卯節點剛度的大小對整體結構自振頻率的高低起決定性作用。

（3）結構的自振頻率隨著屋蓋質量的的增大而降低，結構各部分產生的相對位移反應也大大增加，而其相對應的加速度反應卻因此而減小，說明屋蓋質量的增加可以使斗栱發生較大的水平變形，提高其減震耗能的作用。

［1］ 謝啟芳，杜彬，向偉，等.古建筑木結構燕尾榫節點抗震性能及尺寸效應試驗研究［J］.建筑結構學報，2015，36（3）：112-120.

［2］ 謝啟芳，杜彬，錢春宇，等.古建筑木結構燕尾榫節點彎矩—轉角模型研究［J］.工程力學，2016（8）：39-44.

［3］ 謝啟芳，向偉，杜彬，等.古建筑木結構叉柱造式斗栱節點抗震性能試驗研究［J］.土木工程學報，2015（8）：19-28.

［4］ 高大峰，趙鴻鐵，薛建陽.中國木結構古建筑的結構及其抗震性能研究［M］.北京：科學出版社，2008.

［5］ Fang D.P.，Iwasaki S.，Yu M.H.，et al..Ancient Chinese timber architecture. I： Experimental study［J］.Journal of Structural Engineering-ASCE，2001，127（11）：1348-1357.

［6］ Fang D.P.，Iwasaki S.，Yu M.H.，et al..Ancient Chinese timber architecture.II：Dynamic characteristics［J］.Journal of Structural Engineering-ASCE，2001，127（11）：1358-1364.

［7］ 周乾，閆維明，關宏志.故宮太和殿結構現狀數值模擬研究［J］.中國文物科學研究，2015（2）：79-84.

［8］ 周乾，閆維明，關宏志，等.故宮太和殿靜力穩定構造研究［J］.山東建筑大學學報，2013，28（3）：215-219.

［9］ 周乾，閆維明，關宏志，等.故宮太和殿抗震性能研究［J］.福州大學學報（自然科學版），2013（4）：487-494.

［10］Maeno M.，Saito S.，Suzuki Y..Evaluation of equilibrium of force acting on column and restoring force due to column rocking by full scale test of traditional wooden frames［J］.Journal of Structural and Construction Engineering，Transactions of Architectural Institute of Japan，2007，615：153-160.

［11］Ogawa K.，Sasaki Y.，Yamasaki M..Theoretical modeling and experimental study of Japanese“Watari-ago”joints［J］.Journal of Wood Science，2015，61（5）：481-491.

［12］Kaori F.，Isao S.，Yoshimitsu O.，et al..Static and dynamic loading tests of bracket complexes used in traditional timber structures in Japan［C］.Auckland：The TwelfthWorld Conference on Earthquake Engineering，2000.

［13］Takatani T.，Nishikawa H..Seismic collapsing process analysis of one-story thatched roof wooden structure under strong earthquake ground motion［J］.Journal of Civil Engineering and Construction，2016，5（2）：114-125.

［14］Zhang X.C.，Xue J.Y.，Zhao H.T.，et al..Experimental study on Chinese ancient timber-frame building by shaking table test［J］.Structural Engineering and Mechanics，2011，40（4）：453-470.

［15］隋龑.中國古代木構耗能減震機理與動力特性分析［D］.西安：西安建筑科技大學，2009.

［16］張錫成.地震作用下木結構古建筑的動力分析［D］.西安：西安建筑科技大學，2013.

Parametric analysis of seismic performance of ancient timber-framed buildings

Zhang Xicheng，Ma Hedi，DaiWuqiang，et al.
（School of Civil Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China）

The different structural forms and their parameters directly affect the dynamic characteristics and seismic performance of the ancient timber-framed buildings.The influence of the change of the parameters on the dynamic performance of the structure is studied by the finite element modeling and parameter analysis.Itwill provide reference for the repair and reinforcement of ancient timber-framed buildings.Based on themodel of a single-storey place housemade by Ying Zao Fa Shi of the Song Dynasty，a 3-D beam-spring FEM model is established，which involves the sliding isolation of column root，energy dissipation of Dou-gong and semi-rigid behavior of mortise-tenon joints.Then a comparison is made with the shaking table test under unidirectional earthquake excitations.Furthermore，a parametric analysis is conducted through the change of structural configuration such as mortise-tenon joint，Dou-gong and roof and corresponding parameters.The results show that：with the increase of the lateral stiffness of Dou-gong，the natural frequency of the whole structure converges to the upper limitof2.08 Hz，the ability of shock absorption of the structure becomesweaker.With the increase ofmortise-tenon joints stiffness，the natural frequency of the whole structure converges to the upper limit of 3.26 Hz，while the slippage of the column increased and thelateral displacement of the column reduced.With the reduction of the stiffness of the mortise-tenon joints，the slippage of the column reduced while the lateral displacement of the column increased at the same time.The influence of the stiffness change of the mortise-tenon joints on the building's natural frequency is greater than that of the Dou-gong.The natural frequency of the structure reduced by the increase of the roofmass，while the deformation of the Dou-gong increases and helps improve the seismic capacity of the whole structure.

ancient timber-frame buildings；beam-column elementmodel；structural configuration；seismic capacity

TU366.2

A

1673-7644（2017）05-0426-09

10.12077／sdjz.2017.05.004

2017-08-18

國家自然科學基金項目（51508454）；陜西省自然科學基礎研究基金項目（2016JQ5060）；陜西省教育廳科研計劃項目（15JK1444）；西安建筑科技大學青年科技基金項目（QN1612）；西安建筑科技大學人才科技基金項目（RC1404）

張錫成（1984-），男，講師，博士，主要從事古建筑木結構抗震及加固保護等方面的研究.E-mail：xicheng-zhang＠163.com［*

］

（學科責編：趙成龍）