類石墨烯復雜晶胞光子晶體中的確定性界面態?

賈子源 楊玉婷 季立宇 杭志宏

(蘇州大學物理與光電.能源學部,蘇州納米科技協同創新中心,蘇州 215006)

類石墨烯復雜晶胞光子晶體中的確定性界面態?

賈子源 楊玉婷 季立宇 杭志宏?

(蘇州大學物理與光電.能源學部,蘇州納米科技協同創新中心,蘇州 215006)

(2017年7月24日收到;2017年8月13日收到修改稿)

拓撲絕緣體是當前凝聚態物理領域研究的熱點問題.利用石墨烯材料的特殊能帶特性來實現拓撲輸運特性在設計下一代電子和能谷電子器件方面具有較廣泛的應用前景.基于光子與電子的類比,利用光子拓撲材料實現了確定性界面態;構建了具有C6v對稱性的類似石墨烯結構的的光子晶體復雜晶格;通過多種方式降低晶格對稱性來獲得具有C3v,C3,C2v和C2對稱的晶體,從而打破能谷簡并實現全光子帶隙結構;將體拓撲性質不同的兩種光子晶體擺放在一起,在此具有反轉體能帶性質的界面上,實現了具有單向傳輸特性的拓撲確定性界面態的傳輸.利用光子晶體結構的容易加工性,可以簡便地調控拓撲界面態控制光的傳播,可為未來光拓撲絕緣體的研究提供良好的平臺.

光子晶體,拓撲,谷自由度,界面態

1 引 言

拓撲學是近代發展起來的數學概念,而隨著凝聚態物理的發展,人們發現了一類具有相變、非平庸特性的新型材料——拓撲絕緣體.早在1980年,Klitzing發現了整數量子霍爾效應[1],此系統的特性完全符合拓撲絕緣體的概念.隨后Thouless-Kohmoto-Nightingale-den Nijs關系[2]指出其中量子化的根源是由于拓撲不變量的存在,更是證明了量子化整數對應的是非零陳數.在此系統中出現了一種新的物態拓撲態,在其中電子輸運的表現為完全的背散射抑制和單向傳輸.不同于需要外加磁場破壞時間反演對稱性來實現整數量子霍爾效應,Kane和Mele[3]最早提出在低能量級的單層石墨烯中存在自旋軌道耦合導致的量子自旋霍爾效應,即在石墨烯材料邊界存在一對共軛且自旋方向相反的無能隙拓撲邊界態.我們已經知道以上觀測到的量子化霍爾效應的根本原因是材料的拓撲特性,與具體波動方程無關.從布洛赫定理和能帶性質來看,光子可與電子的性質相比擬,那么光學領域也可能實現類似的光學拓撲絕緣體.

石墨烯是從石墨中剝離出來的、單層碳原子構成的二維晶體結構[4].因其優越的導電導熱高透明度等性能,石墨烯廣泛地應用在很多領域.而且石墨烯具有很多同素異形體結構,如具有更加復雜晶胞結構的石墨炔材料.受石墨烯材料具有的許多新奇物理性質的啟發,人們開始研究與石墨烯具有相同對稱性、相似能帶結構的光子晶體(photonic crystal,PC).構成光子晶體的介電材料具有不同介電常數,它在空間中按一定周期排列[5,6].已經證明可以利用光子晶體來操縱光的傳播行為[7,8],如光子晶體波導[9,10].隨著光子晶體能帶理論的研究,尤其是設計和實驗方法的發展,將拓撲的概念引入光學系統特別是用光子晶體實現拓撲絕緣體,將會不斷拓寬人們構造新型元器件的方法和思路.

迄今已經開展了許多波導傳輸性質的研究工作.其中一方面是利用光子晶體界面態去控制光的傳輸[11].已經研究的構建光子晶體界面態的方法有:構建光子晶體異質結構[12,13]、修飾光子晶體表面[14,15]、堆積擁有共同帶隙的光子晶體等[16].但是這些方法并不能保證界面態一定會產生,需要仔細地調節結構才會產生界面態.不同于之前的研究成果,香港科技大學Chan課題組[17,18]利用一種新的物理機理在一維和二維光子晶體中實現了確定性界面態,即通過操控光子晶體結構參數,簡并的狄拉克錐色散會破缺,從而出現帶隙,能帶性質發生拓撲相變.構成界面的這兩種光子晶體的體能帶拓撲性質反轉,則在兩者共同帶隙處就一定會存在界面態.而且微波段實驗已經在二維正方晶格光子晶體中證明了確定性界面態的存在[19,20].并且還可以同時在多個頻段實現界面態,基于此性質可以用作多帶波導的信息傳輸,甚至是將應用拓展于光頻段實現波分復用器[21].

然而以往的研究工作中,主要研究確定性界面態存在于光子晶體簡單晶格結構中如正方晶格和三角晶格,卻沒有關于復雜晶胞的探討.在本文中,類似于石墨烯材料的復雜晶胞結構,我們構建了具有復雜晶格的光子晶體,嘗試研究復雜晶胞所具備的多種對稱性破缺的可能性.比之類石墨烯的的碳同素異形體在實驗上極難獲取,我們嘗試構造的復雜晶胞光子晶體在實驗上便于實現,而且可以通過調節結構參數和對稱性來操縱色散關系.我們通過四種方式打破光子晶體結構的C6v對稱性,破缺能谷簡并的狄拉克點構建具有反轉體能帶性質的兩個光子晶體;基于界面態存在的拓撲機理,在光子晶體復雜晶胞中實現確定性界面態.本文的研究工作拓寬了操控光子晶體能帶實現拓撲界面態的思路和方法,這些方法簡單易行,而且可以為光波導應用方面提供更廣闊的平臺.

2 類石墨烯復雜晶胞

人們對電子的兩個內稟自由度電荷和自旋的研究促進了自旋電子學的成熟發展和廣泛應用.隨著石墨烯材料的發現和研究,科研工作者操控電子新的自由度能谷,則促進了能谷電子學(valleytronics)的理論和應用探索[22,23].能谷電子學旨在利用能谷作為載體在現代器件中加工處理信息.許多有趣的物理性質已經在理論上得到證明并在實驗中實現,如谷分離(valley filter)[24]、谷霍爾效應(valley Hall e ff ect)[25,26].石墨烯材料具有蜂窩狀晶格,一個原胞結構由兩個碳原子構成,具有C6v對稱性.同時石墨烯具有許多同素異形體,即具有更加復雜多樣的晶胞結構[27].類石墨烯復雜晶胞就是用若干碳原子簇代替原胞上的一個原子.石墨烯材料優異的應用特性源于其特殊的能帶性質.在動量空間中存在的一對不等價的能量局部極值叫做能谷,表現為在第一布里淵區六個角處(K和K′點)石墨烯的能帶簡并在一起,簡并點稱為狄拉克點(Dirac point).K和K′點的能谷是不等價的,其波函數滿足時間反演對稱性.兩者作為能谷自由度的兩個態可以像電子自旋向上、向下態一樣作為信息輸運的載體,被稱作谷贗自旋.我們同樣考慮二維光子晶體.蜂巢晶格中的每個碳原子被一根無限高的介質柱取代,此種光子晶體也具有前述的類似能帶性質;再用三個介質圓柱替代原本的一個圓柱構建類石墨烯的復雜晶胞結構.對比于石墨烯結構在可調控性方面的局限性,此復雜晶胞光子晶體在對稱性方面具有更多可利用的自由度,并且更加容易操縱產生界面態色散關系.

二維光子晶體中確定性界面態的產生與界面通道兩邊結構的不同拓撲性質有關.具體體現為如果構建此界面的兩側光子晶體體能帶性質反轉,那么就一定存在確定性界面態.以最簡單的二維正方晶格光子晶體為例(如圖1(a)),通過調控有效介電常數、晶格常數和介質柱半徑,可以讓能帶在布里淵區中心Γ點發生簡并,這就是通常所說的偶然簡并[28].簡并的能帶色散滿足線性關系,它和電子體系中的狄拉克方程具有對應關系.如此便在光子晶體系統中實現了類似石墨烯結構中的狄拉克錐.通過繼續調節結構參數則可以打開簡并的能帶獲得帶隙.如圖1(b)中,在光子晶體1(PC1)的能帶示意圖中,三條能帶在在Γ點的本征模式分布依次為類似電子系統的s,py,px軌道.然而當我們將結構調整為光子晶體2(PC2),它的體能帶結構則會與PC1發生反轉,如圖1(c)所示.三條能帶中下面簡并的兩條在Γ點為本征模式px,py,而最上面一條為s模式.因此PC1與PC2能帶性質反轉,在兩者反轉能帶共同帶隙中則一定存在界面態.此界面態的存在與否與光子晶體的體性質有關,只需將不同體性質光子晶體擺放一起就一定存在,因此稱為確定性界面態.圖1中的能帶結構均為示意圖,構成此系統的PC1與PC2的參數以及界面態具體傳播性質可以參考文獻[19],這里不再詳述.

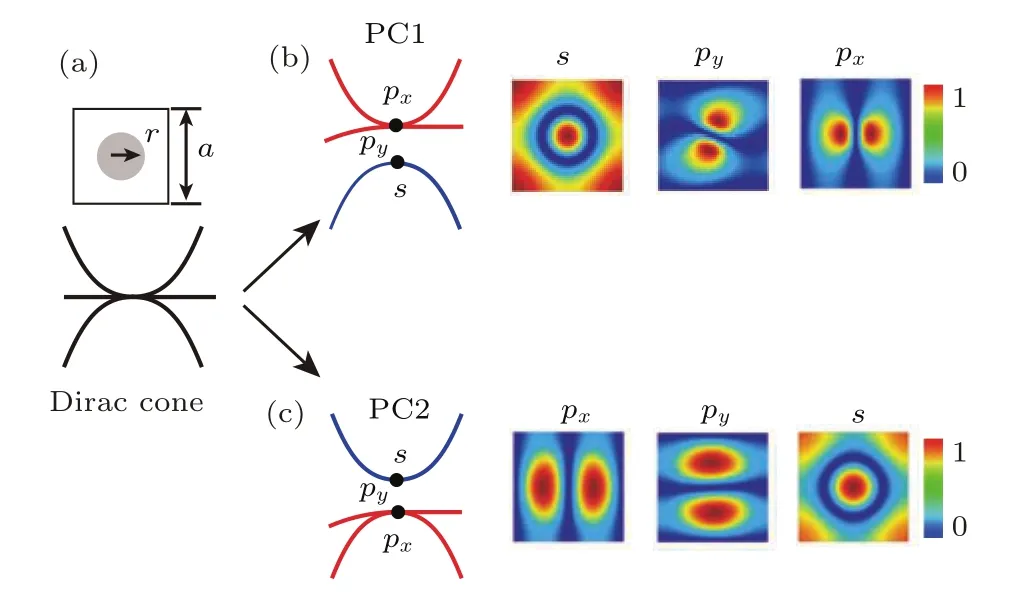
圖1 (a)光子晶體在布里淵區中心的狄拉克錐色散;(b),(c)兩個體能帶反轉的光子晶體Fig.1.(a)Dirac cone dispersion of PC around the center of Brillouin zone center;(b),(c)two inverted band structure of PC1 and PC2.

在本文工作中,基于確定性界面態存在的物理機理,構建擁有更多自由度的復雜晶胞光子晶體,并實現拓撲界面態.圖2(a)為復雜結構的蜂窩狀光子晶體示意圖,深藍色實心圓表示介質柱,淺藍色的區域為背景材料.在紅色實線標示的六角晶胞中可以清晰地看到三個介質圓柱(用綠色凸顯)簇擁在一起構成正三角形(綠色實線),依然具有C6v對稱性,此即為三個介質柱代替一個介質柱構成的復雜晶胞光子晶體.其中相對介電常數ε=7.5的介質圓柱嵌在背景為空氣的材料中.圖中紅色菱形虛線框內的原胞結構,晶格常數為a,介質柱的半徑r=0.1a,到三角形中心的距離為h=0.16a.用COMSOL Multiphysics仿真軟件計算此結構的TM(transverse magnetic)模式能帶,即電場Ez沿著介質柱z軸方向.計算的能帶圖見圖2(b),第一和第二條能帶在布里淵區(插圖中六角形示意圖)中K和K′能谷簡并,簡并點歸一化頻率為0.362c/a(c為真空中光速).由此可見雖然原胞結構變復雜,但是保持對稱性不變光子晶體的能帶性質依然不變.

圖2 (a)復雜光子晶體結構示意圖;(b)光子晶體能帶結構Fig.2.(a)The schematic of the complex lattice PC;(b)PC’s band diagram.

3 C3v對稱性光子晶體中的確定性界面態

通過打破光子晶體的C6v對稱性,可以很容易破缺K和K′點的能谷簡并從而形成帶隙.以圖2原胞中三個介質柱構成的正三角形(灰色區域)中心為基點,在分別對每個三角形拉伸和壓縮柱子之間的距離,調控后得到結構A,如圖3(a)所示.光子晶體A原胞中左下角三個介質圓柱拉伸后到中心的距離為h1=0.18a,而右上角三個柱子壓縮后到中心的距離為h2=0.12a.通過這種方式實現了具有C3v對稱性的光子晶體.從圖3(b)中可以看到在第一條和第二條能帶中間出現完全帶隙,原本在布里淵邊界K點的簡并變成帶隙的下限K1和上限K2點.同時K1和K2點的性質是不同的,如圖3(c)的相位分布.兩者位相分布的手征性是相反的,前者是沿逆時針方向(紫色箭頭所示)相位遞減而后者是順時針方向(綠箭頭所示)相位遞減,旋轉一周回復初始相位,對應角動量m=1和m=?1.而且相位奇點的位置也不同,分別位于拉伸的柱子中心(K1)和壓縮的柱子中心(K2).將拉伸和壓縮柱子到中心距離的方式互換,得到光子晶體結構B,能帶如圖4(a),它的體能帶性質與結構A的能帶是反轉的.可以從圖4(b)K點的相位手征性上很清晰地看到,K1(K2)點相位以順(逆)時針方向遞減.

圖3 (a)兩個相反結構C3v對稱的光子晶體結構示意圖;(b)光子晶體結構A全帶隙能帶;(c)在K1和K2點相反手征性的相位分布Fig.3.(a)The schematic of two inverted PC structures with C3vsymmetry;(b)band diagram with complete band gap for photonic crystal structure A;(d),(e)the inverted chirality of phase distributions at K1 and K2points.

圖4 (a)光子晶體結構B的全帶隙能帶;(b)在K1和K2點相反手征性的相位分布Fig.4.(a)Band diagram with complete band gap for photonic crystal structure B;(b)the inverted chirality of phase distributions at K1and K2points.

可以看到光子晶體A和B的體能帶性質類似,在布里淵區邊界K點附近有完全帶隙,但此帶隙的上下帶邊的能帶手性正好反轉,即在此帶隙光子晶體A和B的體拓撲性質相反.可以預期,如果將光子晶體A和B擺放在一起,在兩者的界面就會有拓撲確定性界面態.我們用超原胞的方法計算了光子晶體A和B沿著kx方向的投影能帶來找尋此拓撲確定性界面態.計算時在界面兩邊各用10個光子晶體原胞構成一個超原胞,周期性邊界條件應用于光子晶體x和y方向.能帶結構如圖5(a)所示,灰色部分是光子晶體的體能帶,綠色和紫色線部分表示界面態的色散關系.能帶一部分是在兩個光子晶體共同帶隙處而另有一部分延伸到體帶里.從色散曲線的斜率可以看出在界面處存在兩個相反方向傳輸的拓撲態.而且兩個態的自旋極化方向相反,分別為自旋向上(紫色線)和自旋向下(綠色線).為了更形象地表征界面態的本征模態,圖5(b)展示了頻率為0.384c/a同時波矢kx= ?0.38(2π/a)的Ez本征場分布(圖5(a)中黑色五角星處).從圖中可以很明顯地看到場局域在兩個光子晶體界面處,而向兩邊衰減很快.

利用光子晶體拓撲態的傳輸性質,可以設計并實現界面態傳輸波導.我們用有限元模擬的方法計算光子晶體界面態的Ez電場分布,如圖6.模擬的上下區域分別由光子晶體結構A和B構成,并包含24×16個復合晶胞結構.區域四周的邊界條件用完美匹配層,這樣可以避免來自邊界的散射.需要用具有手征性的光學激發源才能激發單向的界面態.我們用四個點源陣列(2×2)構建手征性激發源[29].其中,四個點源發射的TM波波函數的初始相位按照不同旋轉方向依次遞減.初始相位按照逆(順)時針方向遞減的激發源和光學渦旋指數即拓撲電荷數m=1(m=?1)的電場分布一致.將拓撲電荷數為m=1的手征性源放在光子晶體A和B界面中間,位置如圖6中白色圓所示,并且光子晶體A置于結構B的下方.在源發射頻率為0.384c/a時激發的單向傳輸界面態場分布如圖6所示,可以觀察到激發的拓撲界面態沿著光子晶體結構A和B的界面通道向左(圖中白色箭頭方向)單向傳輸.從圖5的投影能帶中可以看到,在頻率為0.384c/a時,界面態色散能帶的頻率和體能帶會有部分重疊.所以在此時,界面在傳播的過程中會激發一些體的電場分布.但是由于這些體電場分布相較于界面局域場非常弱,因而并不能對拓撲態的傳輸與應用造成很大的影響.如果用拓撲電荷為m=?1的源則可以激發向右傳播的拓撲態.在兩個光子晶體界面通道傳輸的界面態是受拓撲保護的.界面態具有傳輸單向特性且不受傳播路徑上可能存在的雜質的影響.即使光子晶體材料有雜質不純凈或者是加工制備不完美的情況,拓撲態依然能夠很好地在界面傳輸而不會產生背散射,因此能夠實現拓撲信息輸運從而制備光學器件.這在光學波導方面將具有很大的應用前景.

圖5 (a)光子晶體投影能帶;(b)界面態Ez本征場分布Fig.5.(a)The projected band structure of two PCs;(b)the Ezeigen field distribution of interface state.

圖6 模擬的光子晶體單向傳輸界面態Ez電場分布Fig.6.The simulated Ez field distribution of topological interface state with unidirectional propagation for two PCs.

4 C3對稱性光子晶體中的確定性界面態

在原子尺度上操控石墨烯實現拓撲界面態對技術和條件有一定要求.而人工介質材料微結構單元構建的光子晶體則更容易操作和可調.并且光子晶體可調控的參數有更多的自由度,比如材料的介電常數、晶格常數、占空比等.通過調控結構還可獲得一種C3對稱性的光子晶體,即分別將圖3中的結構A和B圍繞三角形中心逆時針旋轉角度θ=15?,如圖7(a)所示.通過這種打破晶格對稱性的方式依然可以破缺能帶結構中K和K′狄拉克點簡并.圖7(b)和圖7(c)中兩個能帶在K點其性質反轉.調節的兩個結構之間有共同帶隙,經過投影能帶的計算(計算方式同圖5),在兩個光子晶體界面處依然存在確定性界面態,如圖7(d)所示.圖7(e)中五角星標示的是在歸一化頻率為0.384c/a、波矢kx= ?0.4(2π/a)時的界面態Ez本征場分布.利用手征性源激發,基于此結構的界面態色散性質,依然可以像圖6一樣設計單向拓撲態傳輸波導,從而實現信息的輸運與傳播.但通過調節介質柱簇的旋轉角度,可以調控此拓撲界面態的色散關系.

圖7 (a)具有C3對稱的兩個光子晶體結構示意圖;(b),(c)光子晶體能帶結構;(d)投影能帶;(e)界面態Ez本征場分布Fig.7.(a)The schematics of two PCs with C3symmetry;(b),(c)band diagrams of PCs;(d)the projected band structure;(e)the Ezeigen field distribution of interface state.

5 C2v和C2對稱性光子晶體中分別實現確定性界面態

圖8 (a)具有C2v對稱性的兩個光子晶體C和D示意圖;(b)光子晶體C能帶結構;(c)K1和K2點本征場分布Fig.8.(a)The schematics of two PCs with C2vsymmetry;(b)band diagram of PC with structure C;(c)the eigen field distribution at K1and K2points.

進一步打破光子晶體對稱性,還可以用具有C2v對稱的光子晶體中實現確定性界面態.結構如圖8(a)所示,光子晶體介質柱半徑r=0.1a,相對介電常數ε=7.5.將原胞中原本構成正三角形底邊處的兩個介質圓柱,沿y方向(箭頭所示方向)增加距離d1=0.104a,而三角形頂點處圓柱依然保持到中心的距離h=0.16a不變,三個介質柱重新形成等腰三角形,從而得到結構C.結構C的能帶結構如圖8(b),原本K點簡并的狄拉克點被打破因而出現完全帶隙.與之相反的調控得到結構D,即只沿y方向減小底邊處的介質柱的距離d2=0.08a,仍然可以破缺狄拉克點,如圖9(a)所示能帶結構.光子晶體C和D的拓撲性質依然是不同的,兩者能帶反轉.從圖8和圖9(c)中所示的K1和K2點電場振幅本征場分布可以很清楚地看到,在這兩點處能帶性質是反轉的.則兩個光子晶體共同帶隙處存在確定性界面態,如圖10(a).圖10(b)為波矢kx=0.15(2π/a)、歸一化頻率為0.360c/a的Ez本征場分布.

接著將圖8光子晶體C和D結構的原胞中構成兩個等腰三角形的介質柱群以各自三角形中心為原點,均順時針旋轉角度θ=15?,得到光子晶體E和F,示意圖如圖11(a).計算的能帶結構如圖11(b)和圖11(c)所示.雖然進一步降低了晶格對稱性,但是光子晶體的拓撲性質保持不變,依然有拓撲態在兩個能帶反轉的光子晶體界面通道處傳輸,如圖11(d).其中五角星標記處的波矢kx=0.2(2π/a),頻率為0.361c/a,此點的本征場分布如圖11(e).

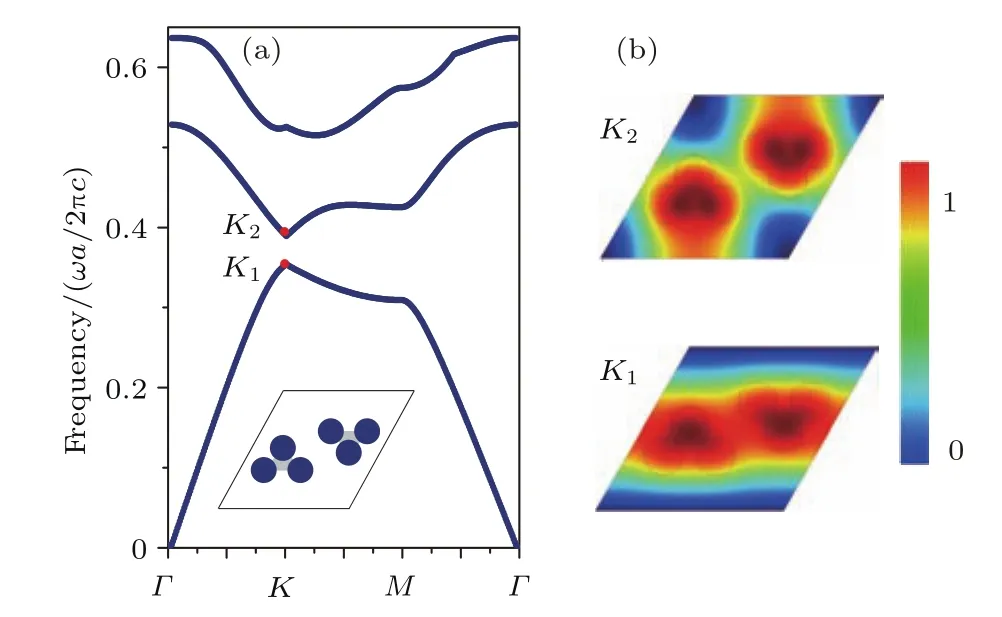
圖9 (a)光子晶體D能帶結構;(b)K1和K2點本征場分布Fig.9.(a)Band diagram of PC with structure D;(b)the eigen field distribution at K1and K2points.

圖10 (a)光子晶體C和D的投影能帶結構;(b)界面態本征場分布Fig.10.(a)The projected band structure;(b)the Ezeigenif eld distribution of interface state.

圖11 (a)具有C2對稱性的兩個光子晶體示意圖;(b),(c)光子晶體能帶結構;(d)投影能帶;(e)界面態Ez本征場分布Fig.11.(a)The schematics of two PCs with C2symmetry;(b),(c)band diagrams of PCs;(d)the projected band structure;(e)the Ezeigen field distribution of interface state.

6 C3v和C2對稱性光子晶體存在確定性界面態

值得強調的是,我們利用復雜晶胞光子晶體產生的拓撲界面態,不依賴于破缺的對稱性方式,只要構建兩個拓撲性質不同即體能帶反轉的光子晶體,那么在界面通道就一定會存在確定性界面態.在具有C3v,C3,C2v和C2對稱性的這四組光子晶體中,任意將體能帶反轉的兩個光子晶體組建在一起,就會有界面態存在.例如C3v對稱的光子晶體A分別與C2v對稱的結構D以及C2對稱的結構F擺放在一起,在共同帶隙處都可以實現拓撲界面態.這里以一組光子晶體為例來證明界面態的存在.如圖12所示,將光子晶體A和F擺放在一起,這兩者的體能帶是反轉的,通過計算得到的投影能帶可知存在確定性界面態.這表明光子晶體界面態不依靠具體結構而取決于體能帶的性質,這在信息輸運方面具有重要的研究意義和價值,因而具有更加廣闊的應用空間.

圖12 (a)光子晶體A和F的原胞結構示意圖;(b)投影能帶Fig.12.(a)The schematics of unit cell for PC A and F;(b)the projected band structure.

7 討 論

用光子晶體構建了類石墨烯復雜晶胞結構.通過多種方式打破蜂窩狀晶格光子晶體的C6v對稱性,獲得了C3v,C3,C2v和C2對稱性的光子晶體,從而可以破缺原本簡并的狄拉克點得到全帶隙的能谷.基于存在確定性界面態的物理機理,就是不依賴于破缺光子晶體對稱性的方式,只取決于界面兩邊兩個光子晶體拓撲性質不同即體能帶性質反轉.我們用兩個復雜晶胞光子晶體構建界面通道并實現了拓撲界面態.利用拓撲態的缺陷免疫和單向性質可以靈活調控光在晶體內部和界面的傳播.相較于石墨烯實現拓撲絕緣體,利用光子晶體的宏觀特性可以更加直接地在實驗中激發、探測光拓撲態,從而提供嶄新的光調控方式.基于界面態在界面的拓撲輸運,還可以為設計新型信息傳播器件提供良好的平臺.另外,光子晶體能谷還有更多可調控的自由度需要去研究與探討.若能夠直接而有效地選擇性激發不等價的光子能谷,進而方便地探測和觀察到能谷偏振現象,這將對拓撲輸運信息具有重大的意義.

感謝蘇州大學物理與光電.能源學部蔣建華教授及武漢大學物理學院邱春印教授對本文的有益討論.

[1]Klitzing K V,Dorda G,Pepper M 1980Phys.Rev.Lett.45 494

[2]Thouless D J,Kohmoto M,Nightingale M P,den Nijs M 1982Phys.Rev.Lett.49 405

[3]Kane C L,Mele E J 2005Phys.Rev.Lett.95 146802

[4]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666

[5]Yablonovitch E 1987Phys.Rev.Lett.58 2059

[6]John S 1987Phys.Rev.Lett.58 2486

[7]Sakoda K 2004Optical Properties of Photonic Crystals(2nd Ed.)(Berlin:Springer)

[8]Joannopoulos J D,Johnson S G,Winn J N,Meade R D 2008Photonic Crystals:Molding the Flow of Light(2nd Ed.)(New Jersey:Princeton University Press)

[9]Mekis A,Chen J C,Kurland I,Fan S,Villeneuve P R,Joannopoulos J D 1996Phys.Rev.Lett.77 3787

[10]Lin S Y,Chow E,Hietala V,Villeneuve P R,Joannopoulos J D 1998Science282 274

[11]Robertson W M,Arjavalingam G,Meade R D,Brommer K D,Rappe A M,Joannopoulos J D 1993Opt.Lett.18 528

[12]Istrate E,Sargent E H 2006Rev.Mod.Phys.78 455

[13]Guo J,Sun Y,Zhang Y,Li H,Jiang H,Chen H 2008Phys.Rev.E78 026607

[14]Meade R D,Brommer K D,Rappe A M,Joannopoulos J D 1991Phys.Rev.B44 10961

[15]Ramos-Mendieta F,Halevi P 1999Phys.Rev.B59 15112

[16]Choi H G,Oh S S,Lee S G,Kim M W,Kim J E,Park H Y,Kee C S 2006J.Appl.Phys.100 123105

[17]Xiao M,Zhang Z Q,Chan C T 2014Phys.Rev.X4 021017

[18]Huang X Q,Xiao M,Zhang Z Q,Chan C T 2014Phys.Rev.B90 075423

[19]Yang Y T,Huang X Q,Hang Z H 2016Phys.Rev.Appl.5 034009

[20]Huang X Q,Yang Y T,Hang Z H,Zhang Z Q,Chan C T 2016Phys.Rev.B93 085415

[21]Yang Y T,Xu T,Xu X F,Hang Z H 2017Opt.Lett.42 3085

[22]Rycerz A,Jakub T J,Beenakker C W J 2007Nature Phys.3 172

[23]Xu X D,Yao W,Xiao D,Heinz T F 2014Nature Phys.10 343

[24]Garcia-Pomar J L,Cortijo A,Nieto-Vesperinas M 2008Phys.Rev.Lett.100 236801

[25]Xiao D,Yao W,Niu Q 2007Phys.Rev.Lett.99 236809

[26]Mak K F,McGill K L,Park J,McEuen P L 2014Science344 1489

[27]Enyashin A N,Ivanovskii A L 2011Phys.Status Solidi248 1879

[28]Huang X Q,Lai Y,Hang Z H,Zheng H H,Chan C T 2011Nature Mater.10 582

[29]Yang Y T,Xu Y F,Xu T,Wang H X,Jiang J H,Hu X,Hang Z H 2016 arXiv:1610.07780v1

PACS:78.67.Pt,73.20.At,42.70.Qs,61.48.GhDOI:10.7498/aps.66.227802

*Project supported by the National Natural Science Foundation of China(Grant No.11574226),the Natural Science Foundation of Jiangsu Province,China(Grant No.BK20170058),and the Priority Academic Program Development(PAPD)of Jiangsu Higher Education Institutions,China.

?Corresponding author.E-mail:zhhang@suda.edu.cn

Deterministic interface states in photonic crystal with graphene-allotrope-like complex unit cells?

Jia Zi-Yuan Yang Yu-Ting Ji Li-Yu Hang Zhi-Hong?

(College of Physics,Optoelectronics and Energy and Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China)

24 July 2017;revised manuscript

13 August 2017)

Topological insulators have aroused much research interest in condensed matter physics in recent years.Topological protected edge states can propagate unidirectionally and backscattering free along the boundaries of the topological insulators’which will be important for future electronic devices for its immunity to defects.Topology is dependent only on the symmetry of lattice of the system rather than its speci fic wave form.Thus,based on the analogy between electronics and photons,photonic topological insulator has also been demonstrated both theoretically and experimentally.Graphene,composed of a monolayer of carbon atoms in honeycomb lattice,exhibits unusual properties due to its intriguing band diagram.Many types of graphene allotropes have been proposed theoretically.However,due to fabrication difficulties,most of graphene allotropes are unavailable.Here,we propose to study two dimensional(2D)photonic crystal(PC)with complex lattices,similar to that of graphene allotrope.The complex PC structure provides more degrees of freedom in manipulating its symmetry.

Interface states can also exist in the interface region between two PCs,if they have di ff erent topological properties.Without any surface decoration,deterministic interface states can be created when bulk photonic band inversion can be induced and are demonstrated theoretically and experimentally in 2D PCs with square lattice.By controlling the parameters of PCs,their bulk photonic band properties are engineered and topological phase transition occurs.By inverting the bulk photonic band properties,interface states exist in the common band gaps for two PC systems in the gapped region.Similarly,we proceed to complex honeycomb lattice of PCs.By lowering its originalC6vsymmetry toC3v,C3,C2vand evenC2symmetry,the degeneracies of valley Dirac dispersion at the corners of Brillouin zone are lifted.Photonic band inversion occurs in all four symmetries and the deterministic interface states are numerically realized in the interface region between two PCs.Unidirectional propagation of interface state immune to backscattering along the interface channels is demonstrated if a source with proper optical vortex index is utilized.Due to its easy fabrication,PC is a perfect platform to explore the topological properties of complex lattice and these acquired topological optical states can be of bene fit to the control the propagation of light in the photonic waveguide.

photonic crystal,topology,valley,interface state

10.7498/aps.66.227802

?國家自然科學基金(批準號:11574226)、江蘇省自然科學基金(批準號:BK20170058)和江蘇省高校優勢學科建設工程資助的課題.

?通信作者.E-mail:zhhang@suda.edu.cn