基于等效磁路法的軸向磁場磁通切換型永磁電機靜態特性分析*

徐 妲, 趙旭鳴, 林明耀, 付興賀, 郝 立, 李欣哲

(1. 東南大學 電氣工程學院,江蘇 南京 210096;2. 國家電網江蘇省電力公司檢修分公司,江蘇 南京 210096;3. 國家電網江蘇省無錫供電公司,江蘇 無錫 214100)

基于等效磁路法的軸向磁場磁通切換型永磁電機靜態特性分析*

徐 妲1, 趙旭鳴2, 林明耀1, 付興賀1, 郝 立1, 李欣哲3

(1. 東南大學 電氣工程學院,江蘇 南京 210096;2. 國家電網江蘇省電力公司檢修分公司,江蘇 南京 210096;3. 國家電網江蘇省無錫供電公司,江蘇 無錫 214100)

軸向磁場磁通切換型永磁(AFFSPM)電機是一種軸向長度短、轉矩密度高的新型永磁電機。該電機磁場呈三維分布，與徑向磁場電機不同，需要對該電機進行三維有限元分析，從而增加了電機分析和優化時的計算時間和成本。基于等效磁路法分析了AFFSPM電機的靜態特性，建立了AFFSPM電機的非線性等效磁路模型，采用該模型計算、分析了氣隙磁密、空載永磁磁鏈、反電動勢和電感等特性，并與采用三維有限元方法的計算結果進行比較，驗證了AFFSPM電機等效磁路模型的準確性，表明等效磁路模型適用于AFFSPM電機初始設計和分析。

軸向磁場；磁通切換；等效磁路法；電磁特性

0 引 言

雙定子或雙轉子結構的軸向磁場磁通切換型永磁(Axial Field Flux-Switching Permanent Magnet,AFFSPM)電機因其結構緊湊、體積小、工作穩定、轉矩密度高和效率高等優點備受國內外研究人員的關注和研究[1-7]。AFFSPM電機較短的軸向長度使得該電機更適用于直接驅動控制系統如風力發電、電動汽車等。

電機靜態特性的準確分析是電機設計和優化的前提條件。目前分析電機電磁性能的計算方法主要為數值法和解析法。其中，解析法計算繁瑣，需要推導大量公式，并在特定的簡化條件下求解方程組，而計算過程中諸如磁路飽和、漏磁等因素無法精確地考慮在解析式中，導致計算準確度較低，一般只用于定性分析。故定量分析時一般采用數值法，常用方法包括有限元法和等效磁路法。三維有限元法可同時考慮多種效應的影響，結合功能強大的有限元計算軟件，實現精度較高的電磁場分析，但分析計算時間較長，較適合對于結構參數已確定的電機進行分析計算，對于需要多次計算不同結構參數下的初始設計和靜態特性分析來說，有限元法較不便且計算成本較高。等效磁路法是電機工程中常用的磁場近似計算方法，將場化路，可以兼顧磁路飽和、永磁及電樞磁場相互作用等影響，實現電機磁場分布和參數的快速求解，適用于電機初始設計。等效磁路法在不同類型永磁電機的電磁設計中應用廣泛[8-14]。文獻[9-10]基于等效磁路模型對徑向磁場磁通切換電機的電磁特性進行研究。文獻[11-14]對軸向磁場表貼式盤式電機的等效磁路模型進行了研究和優化。

與徑向磁場類型的電機不同，AFFSPM電機的轉子旋轉方向與永磁磁通方向垂直，且同時存在軸向和周向路徑的磁通，電機磁場呈三維非線性分布，難以將其簡化為二維磁場分析計算，使得其分析設計過程難度加大。因此，對于AFFSPM電機來說，電機的性能預估分析和優化設計需建立一個簡單、準確的等效磁路模型。

本文針對三相12/10極AFFSPM電機，推導并建立該電機的考慮磁路飽和以及氣隙漏磁影響的等效磁路模型。在等效磁路模型的基礎上，求解、分析該電機的靜態特性，包括氣隙磁密、空載永磁磁鏈、反電動勢和繞組電感，并將計算結果與三維有限元法分析結果進行對比驗證。

1 電機結構

AFFSPM電機由兩個定子和一個轉子組成，如圖1所示，轉子置于中間，與兩個外定子形成雙氣隙。12/10極AFFSPM電機每個定子由12個U型鐵心、12塊永磁體和12個線圈組成。線圈繞于兩個相鄰U型鐵心齒上，中間嵌入永磁體，每4個線圈串聯成一相繞組。單個定子上永磁體沿切向交替充磁，兩側定子正對的永磁體充磁方向相反。電機轉子無磁軛，結構與開關磁阻電機類似。10個轉子齒均勻設置在非導磁圓環的外圓周上，轉子齒為卷繞式沖片疊壓而成。該電機軸向長度短，槽滿率高，具有較高的功率密度和效率。

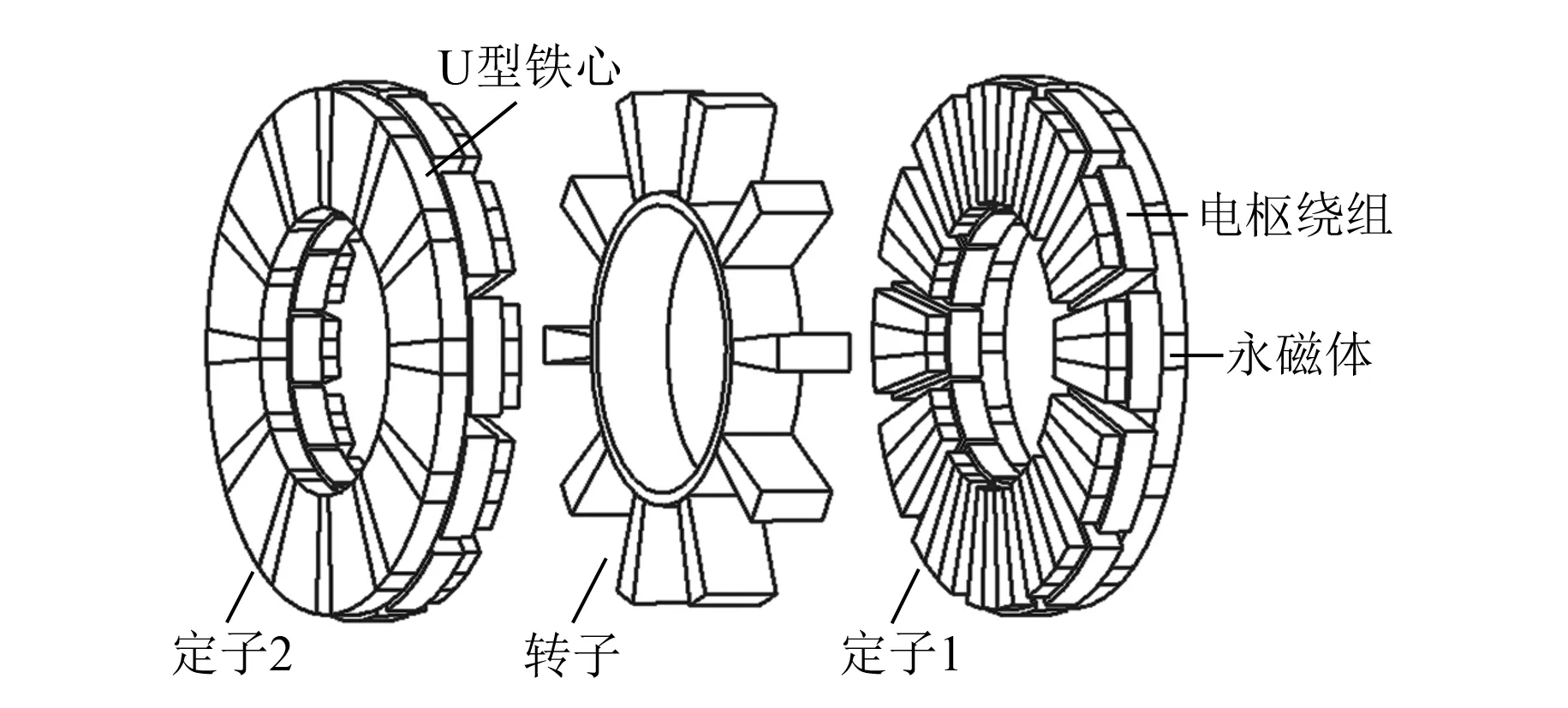
圖1 三相12/10極AFFSPM電機結構圖

2 等效磁路模型

等效磁路法適用于不同類型電機的磁場近似計算。對于AFFSPM電機來說，其等效磁路模型包括定子鐵心、永磁體、轉子鐵心和氣隙4個部分。AFFSPM電機的盤式結構使得磁通密度沿徑向近似均勻分布，故電機的靜態特性可以簡化在平均半徑處計算。

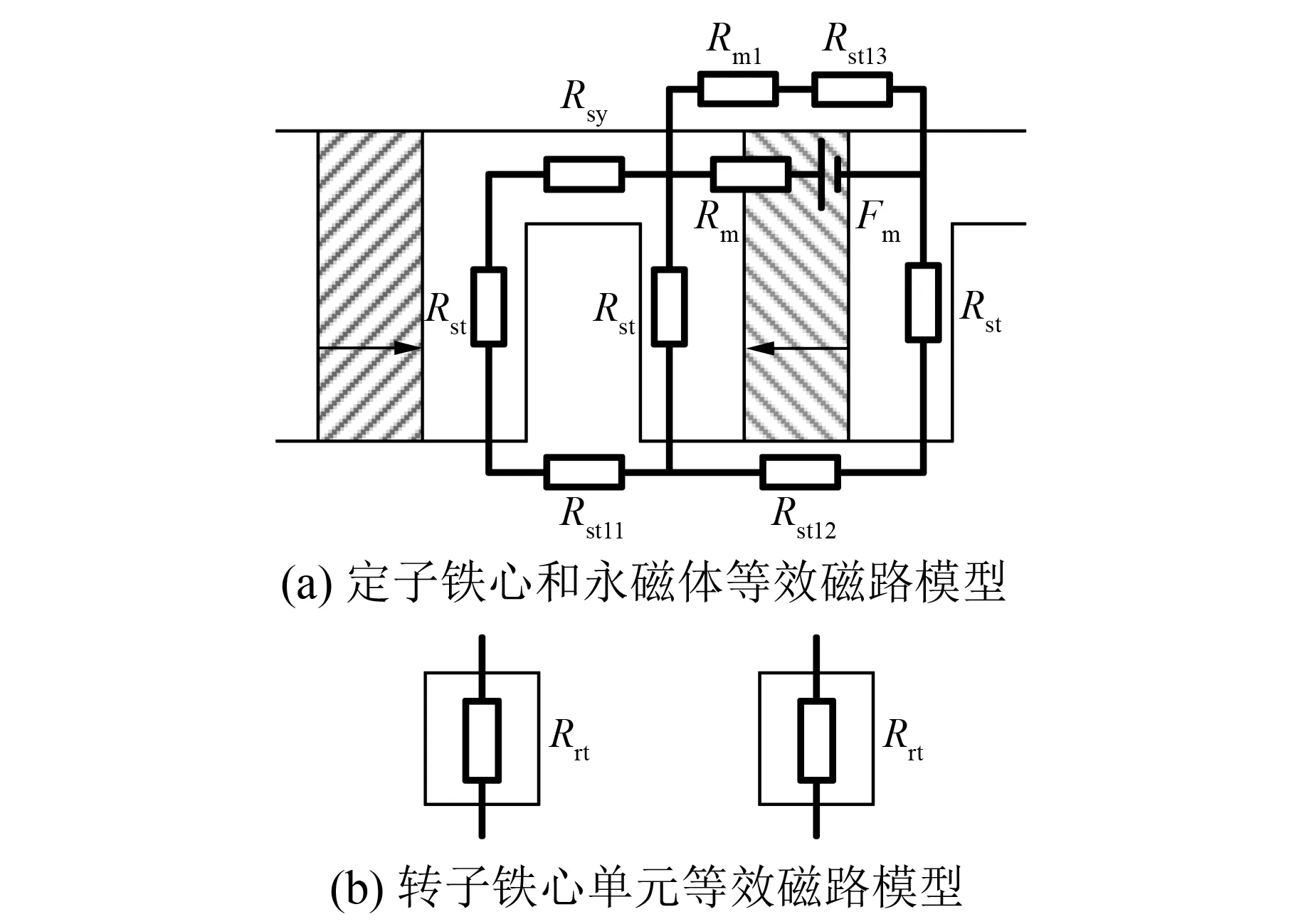
圖2 定、轉子鐵心與永磁體等效磁路模型

定、轉子鐵心和永磁體的局部等效磁路模型如圖2所示。考慮磁路飽和的影響，鐵磁材料采用非線性磁阻Rsy、Rst、Rrt。定子齒槽之間的漏磁通以及端部漏磁由磁阻Rstl1、Rstl2和Rstl3體現；轉子齒距較長，其齒間漏磁通不予考慮。等效磁路模型中永磁體等效為磁動勢源Fm和內磁阻Rm，同時采用漏磁阻Rml體現永磁體端部漏磁。對于定、轉子鐵心來說，其相對磁導率隨鐵心內磁通密度而變化，故等效磁路建模過程中依據軟磁復合材料的磁化曲線進行迭代計算非線性磁阻，從而考慮磁路飽和現象。

以上各磁阻和磁動勢可由式(1)～式(9)計算：

式中:μ0、μr——真空磁導率、相對磁導率；

hst、hm、hsc、hrt——定子齒寬、永磁體磁化厚度、定子單元寬度、轉子齒寬，如圖3所示；

le——AFFSPM電機徑向有效長度，定義為le=(Dso-Dsi)/2；

ls、lsy、lst——定子軸向長度、定子軛部厚度、定子齒軸向長度；

lr、g——轉子軸向長度、氣隙長度；

Ps——定子單元數;

Dso、Dsi——定子外徑、內徑；

HC、Br——永磁體矯頑力、剩余磁通密度。

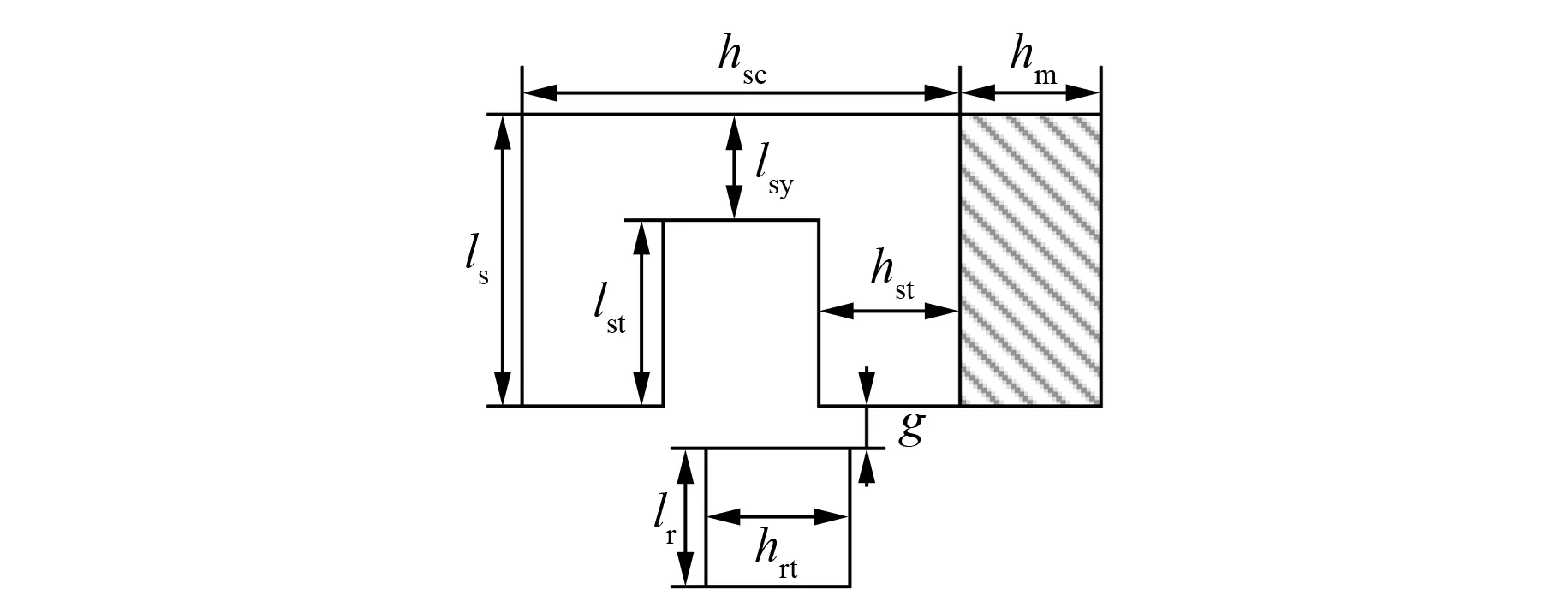
圖3 AFFSPM電機結構參數標示

在AFFSPM電機等效磁路模型中，定、轉子之間的氣隙磁阻是關鍵參數。由于空氣的磁導率遠遠小于導磁材料的磁導率，氣隙磁阻的計算精度對電機等效磁路模型的準確性有很大影響。AFFSPM電機是雙凸極結構，定、轉子齒間存在明顯的邊緣效應和局部飽和現象，且與定、轉子齒的相對位置、電樞繞組電流大小相關，因此氣隙磁阻很難用數學式精確表達。

從計算精度和實用性角度考慮，本文采用分割法研究AFFSPM電機的氣隙磁阻近似表達式。根據AFFSPM電機氣隙磁場的分布規律，利用磁力線把AFFSPM電機氣隙分成若干規則形狀的磁通管，并使各個磁通管中的磁力線規律盡可能相同，如圖4所示。在滿足一定計算精度的情況下，假定氣隙磁通僅沿著軸向分布，即垂直進入定、轉子鐵心端面。求出圖4中各個磁通管的磁阻后，根據各個磁阻之間的串、并聯關系可得整個氣隙的總磁阻。根據電機轉子轉動過程中所在的位置，將轉子位置劃分為若干個區間，如圖5所示。每個區間內磁通分布規律基本一致，故區間內氣隙磁阻可根據相同磁阻公式進行計算。定轉子齒間氣隙磁阻可以表示為基本氣隙磁阻類型的組合，根據各磁通管的形狀參照基本類型的公式進行計算[9]。

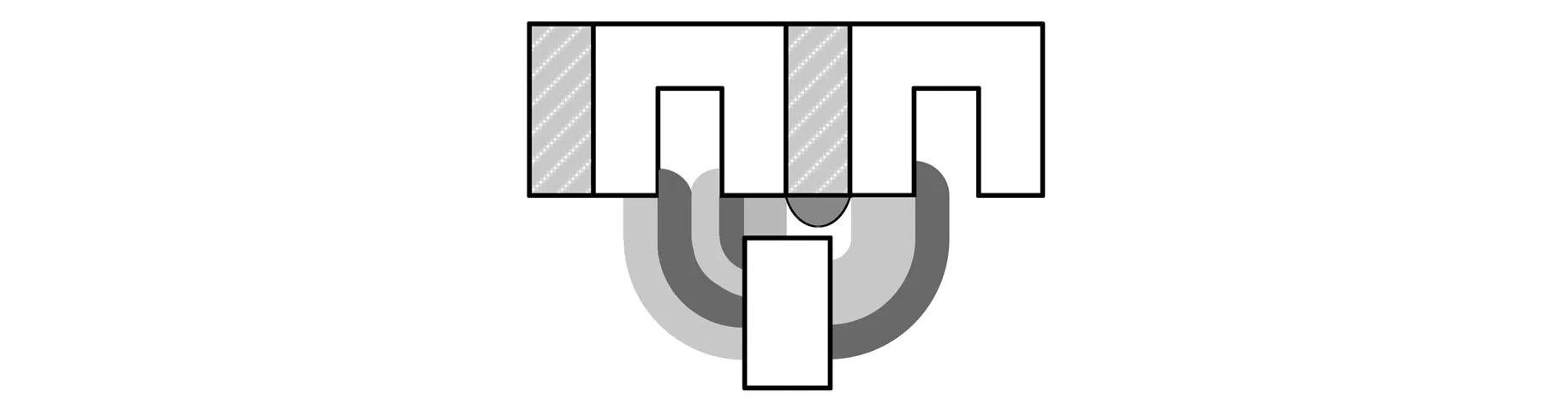
圖4 氣隙磁阻組成局部示意圖

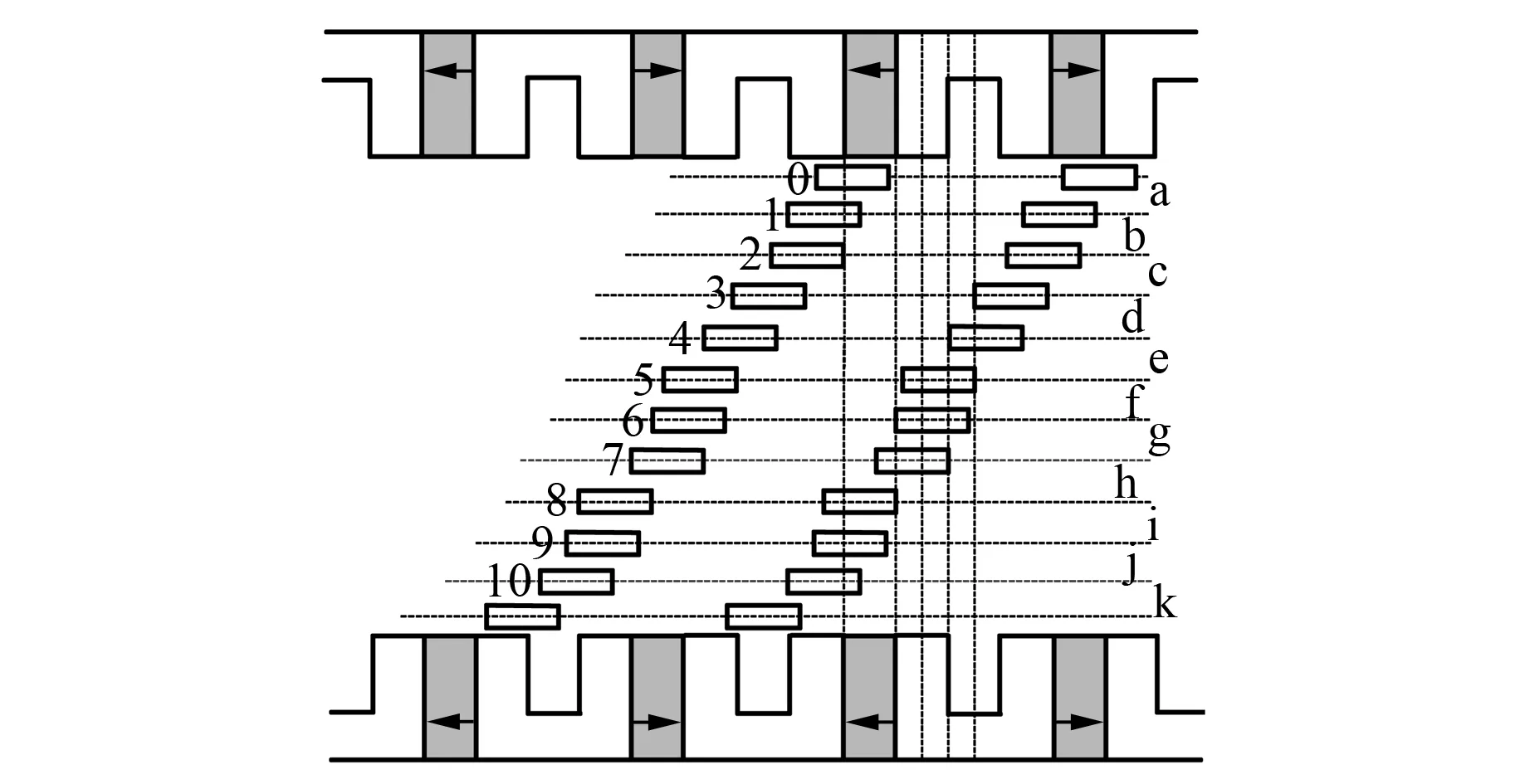
圖5 電機轉子位置區間劃分示意圖

根據AFFSPM電機的磁場分布和磁導分類，將以上各個不同部分的等效磁路結合在一起，可建立AFFSPM電機的等效磁路模型，如圖6所示。

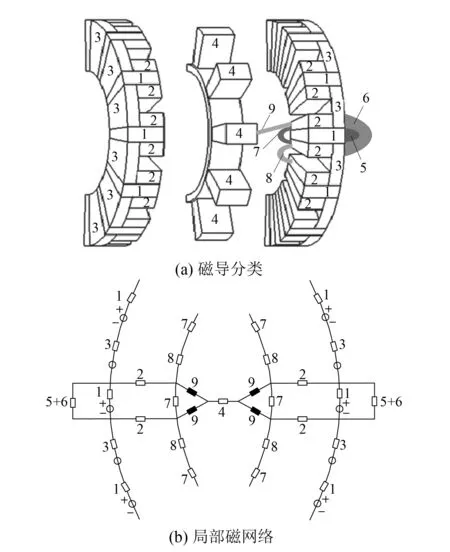
圖6 局部結構等效磁路圖

AFFSPM電機等效磁網絡中，等勢面的磁勢節點位置可分別固定在定子和轉子中，與轉子位置角θr無關，也即定、轉子極間磁通路徑的改變可等效為定、轉子極磁勢節點之間的并聯支路發生改變，這樣轉子運動過程中定子、轉子的等效磁網絡不需要重新建立。

3 靜態特性分析與驗證

通過對AFFSPM電機等效磁網絡的求解，可以得到電機的靜態特性，包括氣隙磁密、空載永磁磁鏈、反電動勢和繞組電感。為了驗證上述等效磁路模型的準確性，對AFFSPM電機采用Ansys有限元分析軟件進行仿真，并與等效磁路分析結果進行比較。電機主要結構參數如表1所示。

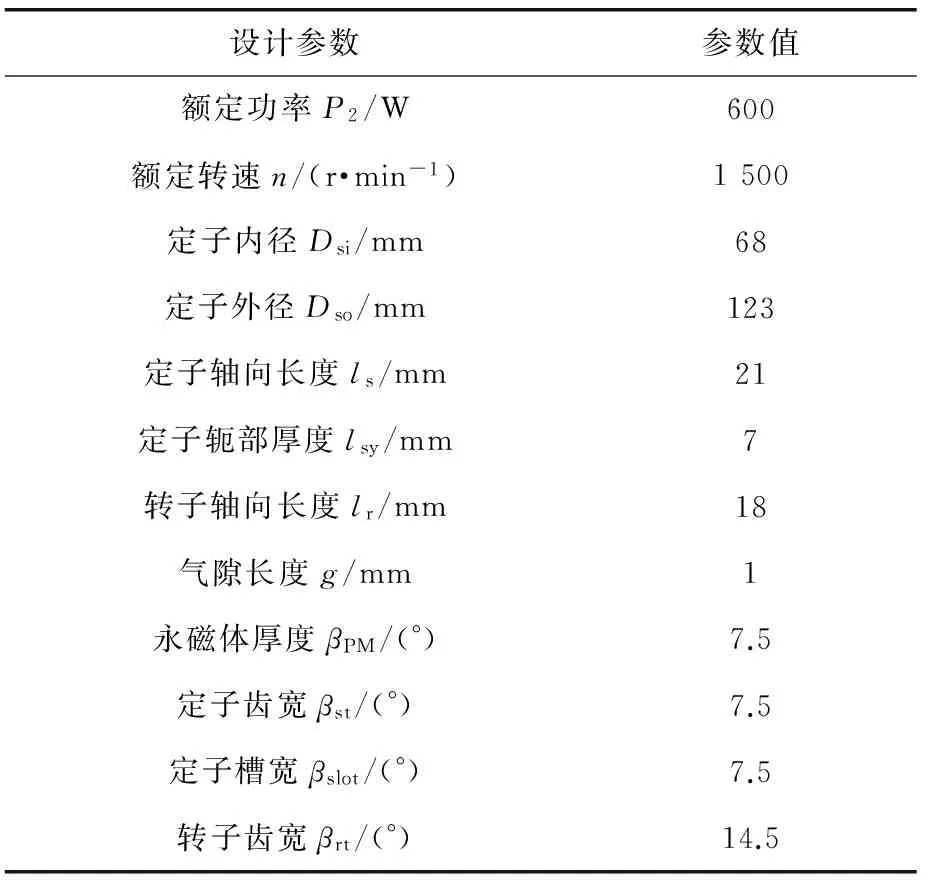
表1 AFFSPM電機結構參數

3.1氣隙磁密

氣隙磁通密度分布對電機特性分析很重要，圖7為由有限元法和等效磁路法計算得到的半個圓周上平均半徑處氣隙磁密分布情況。由圖7可見，磁路法分析與有限元分析的波形基本重合，峰值處數值有所差別，磁路法計算的磁密峰值比有限元計算結果略高,這是由于等效磁路法建模過程中假設氣隙磁通均為垂直轉子齒面(即軸向分布)且進行二維計算，有限元分析時對于AFFSPM建立了三維有限元模型，實際平均半徑處氣隙磁通存在其他方向的分量。

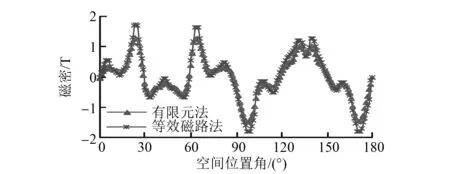
圖7 半圓周平均半徑處空載氣隙磁密

3.2空載永磁磁鏈

對于AFFSPM電機來說，以A相為例，單相繞組的空載永磁磁鏈ΦpA為

ΦpA=ΦA+ΦA′=

式中:ΦA、ΦA′——定子1、2上A相繞組的磁鏈；

ΦA1、ΦA2、ΦA3、ΦA4、ΦA1′、ΦA2′、ΦA3′、ΦA4′—— 定子1、2上A相繞組每個線圈的磁鏈。

圖8所示為由有限元法和等效磁路法計算得到的A相繞組空載永磁磁鏈波形。兩種方法分析的結果基本吻合，等效磁路法計算所得的磁鏈幅值比有限元分析所得結果略大，在可接受的誤差范圍內。兩者偏差原因是假定氣隙磁通僅沿著軸向分布所致，引入漏磁系數可使計算結果更為精確。

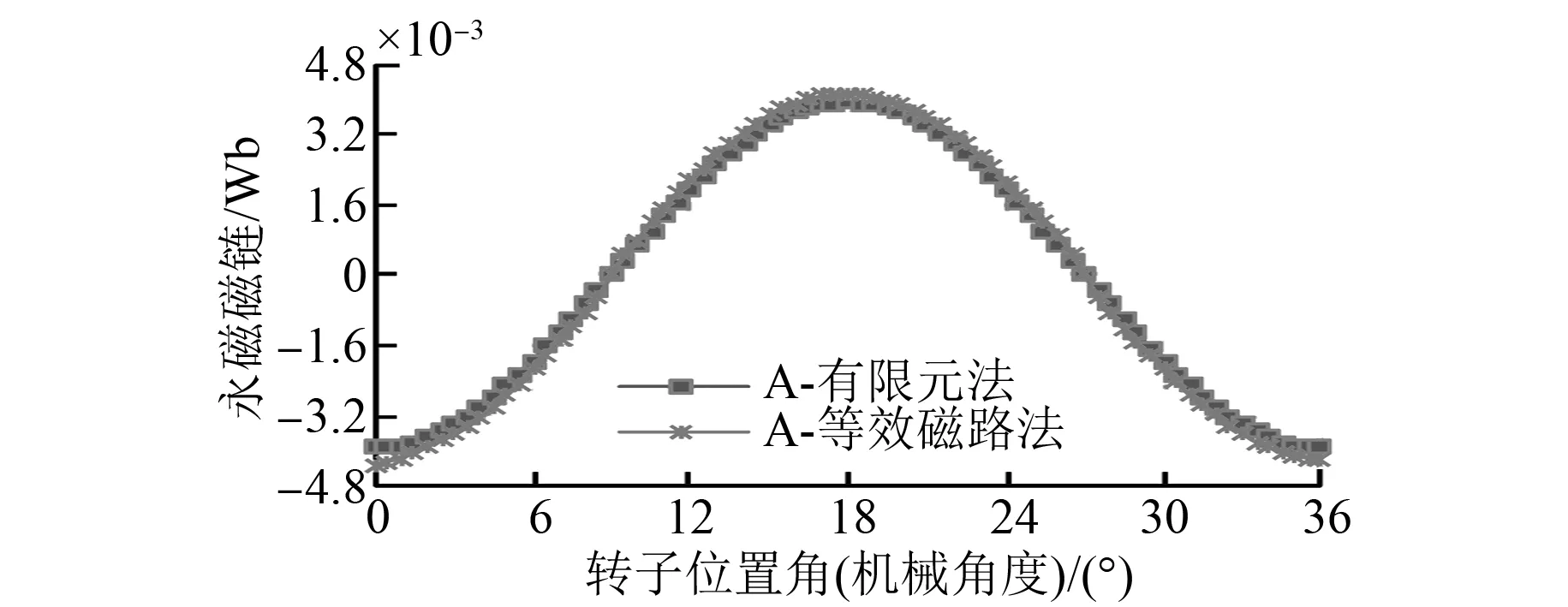
圖8 單匝空載永磁磁鏈

3.3空載反電動勢

A相反電動勢由A相磁鏈求導可得：

如圖9所示為由有限元法和等效磁路法計算得到的A相繞組空載反電動勢波形。兩種方法計算結果基本重合，但在反電動勢峰值位置，等效磁路法的計算值明顯低于有限元法的計算值。此外，磁路法計算所得反電動勢諧波含量較高，使得波形平滑度明顯低于有限元法分析結果。

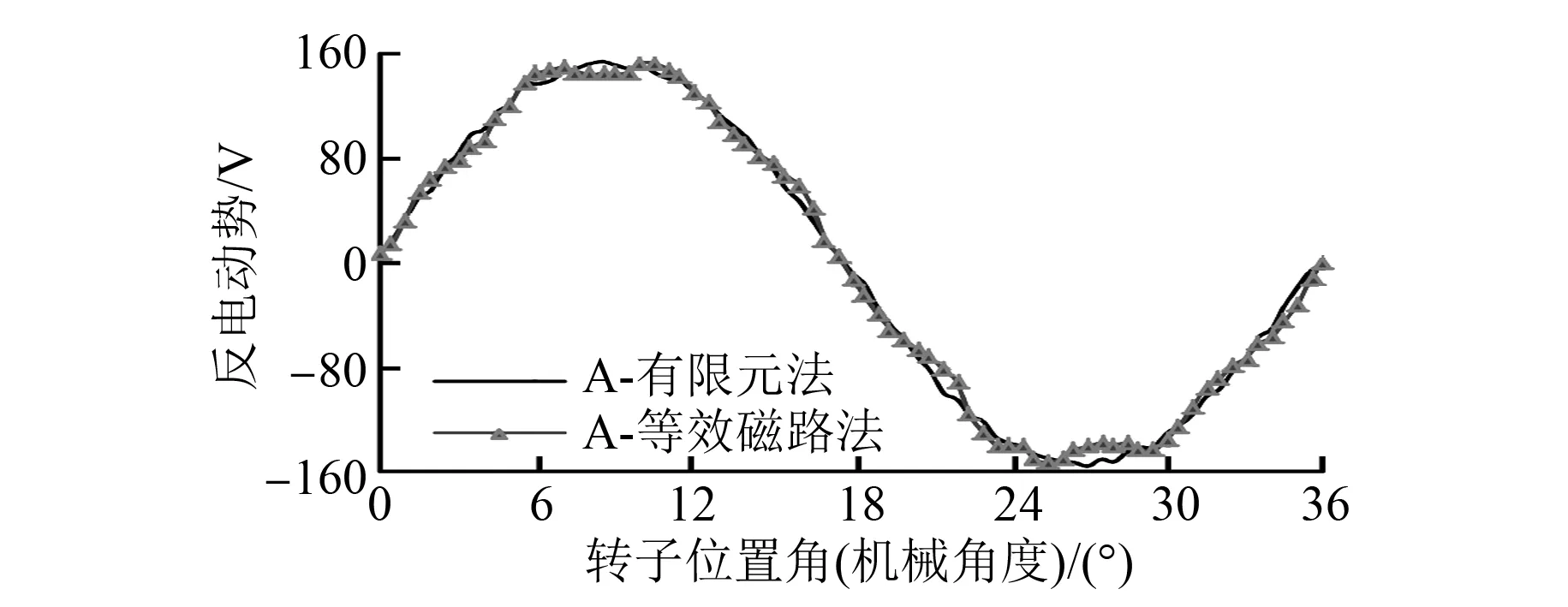
圖9 單相空載反電動勢

3.4電感特性

以A相為例，AFFSPM電機電樞相繞組的自感La和互感Man的計算方法如下：

式中:ΦpmA——A相繞組匝鏈的空載永磁磁鏈；

ΦpA——某相繞組通入電流后A相繞組匝鏈的磁鏈；

ia、in——A相和B相(或C相)繞組通入的電流。

圖10為由有限元法和等效磁路法計算得到的A相繞組不飽和電感和飽和電感波形。由圖10可見，兩種方法計算所得的A相繞組不飽和自感和互感的波形具有較好的一致性，而磁路法計算所得的A相繞組飽和自感和互感均低于有限元法分析結果，電感的計算結果與磁通計算值相關。

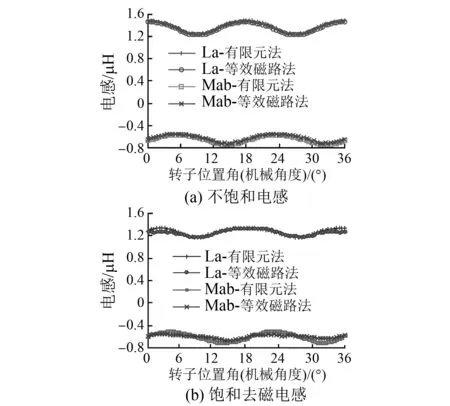
圖10 相繞組自感和互感

4 結 語

本文基于等效磁路法提出了三相12/10極AFFSPM電機的簡單而準確的磁場計算模型。該模型考慮了鐵心磁路飽和以及各部分漏磁的影響。對于鐵心飽和的影響，該模型采用迭代法計算非線性鐵心磁阻；對電機定轉子各部分分別建立磁路模型，通過改變氣隙串聯磁路來反映電機轉子運動過程中氣隙磁場的分布，有效簡化等效磁路模型。在電機等效磁路模型的基礎上，求解了電機的靜態特性，包括氣隙磁密、空載永磁磁鏈、反電動勢和電樞繞組電感。將三維有限元法分析結果與等效磁路法分析結果進行對比，驗證了所建立的等效磁路模型的準確性。本文所建立的等效磁路模型能在保證較高計算精度的前提下，有效節省計算時間，適用于該種電機的初始設計和電磁優化，對其他類型的軸向永磁電機的分析設計有一定參考價值。

[1] LIN M Y, HAO L, LI X, et al. A novel axial field flux-switching permanent magnet wind power generator[J].IEEE Transactions on Magnetics,2011,47(10): 4457-4460.

[2] HAO L, LIN M Y, XU D, et al. Static characteristics of a novel axial field flux-switching permanent magnet motor with three stator structures[J].IEEE Transactions on Magnetics,2014,50(1): 1-4.

[3] HAO L, LIN M Y, LI W, et al. Novel dual-rotor axial field flux-switching permanent magnet machine[J].IEEE Transactions on Magnetics,2012,48(11): 4232-4235.

[4] ZHAO W L, LIPO T A, KWON B I. A novel dual-rotor, axial field, fault-tolerant flux-switching permanent magnet machine with high-torque performance[J].IEEE Transactions on Magnetics,2015,51(11): 1-4.

[5] 郝立,林明耀,徐妲,等.軸向磁場磁通切換型永磁電機齒槽轉矩抑制[J].電工技術學報,2015,30(2): 21-26.

[6] KABIR M A, AHMED A, HUSAIN I. Axial flux segmental rotor flux-switching synchronous motor[C]∥ IEEE Conference on Energy Conversion Congress and Exposition (ECCE),2015: 2148-2152.

[7] 裴召剛,林明耀,趙紀龍,等.軸向磁場磁通切換型永磁電機矢量控制[J].電機與控制應用,2013,40(7): 37-42.

[8] 葛笑,張琪,黃蘇融.磁極分割型混合勵磁電機等效磁路法分析[J].電機與控制應用,2006,33(1): 11-16.

[9] ZHU Z Q, PANG Y, HOWE D, et al. Analysis of electromagnetic performance of flux-switching permanent magnet machines by non-linearadaptive lumped parameter magnetic circuit model[J].IEEE Transactions on Magnetics,2005,41(11): 4277-4287.

[10] WEI H, GAN Z, MING C, et al. Electromagnetic performance analysis of hybrid-excited flux-switching machines by a nonlinear magnetic network model[J].IEEE Transactions on Magnetics,2011,47(10): 3216-3219.

[11] QU R H, LIPO T A. Analysis and modeling of air-gap and zigzag leakage fluxes in a surface-mounted permanent magnet machine[J].IEEE Transactions on Industrial Applications,2004,40(1): 121-127.

[12] 黃允凱,周濤.基于等效磁路法的軸向永磁電機效率優化設計[J].電工技術學報,2015,30(2): 73-79.

[13] KANO Y, KOSAKA T, MATSUI N. A simplenonlinear magnetic analysis for axial-flux permanent-magnet machines[J].IEEE Transactions on Industrial Electronics,2010,57(6): 2124-2138.

[14] 宮曉,徐衍亮.軸向磁場盤式永磁電機等效磁路網絡及氣隙漏磁的分析計算[J].電機與控制學報,2013,17(10): 59-64.

ElectromagneticPerformanceAnalysisofAxialFieldFlux-SwitchingPermanentMagnetMachineUsingEquivalentMagneticCircuitMethod*

XUDa1,ZHAOXuming2,LINMingyao1,FUXinghe1,HAOLi1,LIXinzhe3

(1. Department of Electrical Engineering, Southeast University, Nanjing 210096, China;2. Jiangsu Electric Power Maintenance Branch Company, State Grid, Nanjing 210096, China;3. Wuxi Power Supply Company of Jiangsu Province, State Grid, Wuxi 214100, China)

Axial field flux-switching permanent magnet (AFFSPM) machine was a novel machine with short axial length and high torque density. The 3-D distributed magnetic flux of the AFFSPM machine required the 3-D field analysis which increased the calculation time and cost of analysis and optimization. A nonlinear equivalent magnetic circuit model of the AFFSPM machine was built, and the static characteristics of the AFFSPM machine, including the air-gap flux density, permanent magnetic flux linkage, back electromotive force and inductance characteristics were calculated and analyzed based on equivalent magnetic circuit model. The calculated results were compared with those predicted by 3-D finite element method. The analysis results with two methods consist well, the feasibility of the proposed equivalent magnetic circuit model were verified.

axialfiled;flux-switching;equivalentmagneticcircuit;electromagneticperformance

國家自然科學基金項目(51277025，51577024)；江蘇省自然科學基金項目(BK20161425)

徐 妲(1989—)，女，博士研究生，研究方向為永磁電機設計、分析。趙旭鳴(1987—)，男，碩士，中級工程師，研究方向為電機設計，電網運維。林明耀(1959—)，男，教授，博士生導師，研究方向為電機系統及其控制技術。

TM 301.2

A

1673-6540(2017)11- 0079- 06

2017 -03 -14