圖形計算器在對勾函數單調性教學中的應用
蔣培杰+馬恩榮
【摘 要】本文借助圖形計算器技術,以對勾函數單調性的教學為例,通過讓學生經歷對勾函數性質的發現過程,體驗操作、觀察、歸納、發現和證明的學習過程,從而感知圖形計算器技術在數學操作、觀察、歸納、發現和證明中的重要作用,并進一步提出一般數學教育技術對數學認知活動的三大功能:提供驗證、啟示發現和促進理解。
【關鍵詞】圖形計算器 對勾函數 操作 觀察 歸納 發現 證明
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2017)09B-0081-03
現代信息技術已經對全世界政治、經濟和文化產生了重大而深遠的影響。被喻為“移動數學實驗室”的圖形計算器作為一種現代數學教育技術工具,對數學教育產生積極的影響。圖形計算器是一種具有函數(解析式、參數)作圖、動態圖形、方程求解、數據處理、簡單編程和 CAS 功能的計算器。它不僅能夠進行數值運算和簡單的符號運算,而且還可以直觀地繪制各種方程曲線、函數圖象,可以進行軌跡跟蹤、動態演示,具有一定的交互性,是一種現代手持技術。本文選取對勾函數單調性的發現和證明的教學過程為例,闡述圖形計算器在學生數學操作、觀察、歸納、發現和證明中的作用。
一、對勾函數簡介
(一)對勾函數的概念
函數 的圖象是對稱的“雙勾”,因此一般形如 的函數稱為對勾函數。對勾函數作為一種特殊的函數模式有許多特殊的性質,它的圖象優美。學習對勾函數可以幫助學生理解函數圖象與性質之間的關系,感悟利用函數圖象研究函數性質的思想方法。此外,對勾函數的諸多性質有著廣泛的應用,在各類測試和高考試題中都有考查。當 ab<0 時,函數 的單調性容易確定,因此,對勾函數單調性的學習的難點在于,當 ab>0 時,函數 的單調性。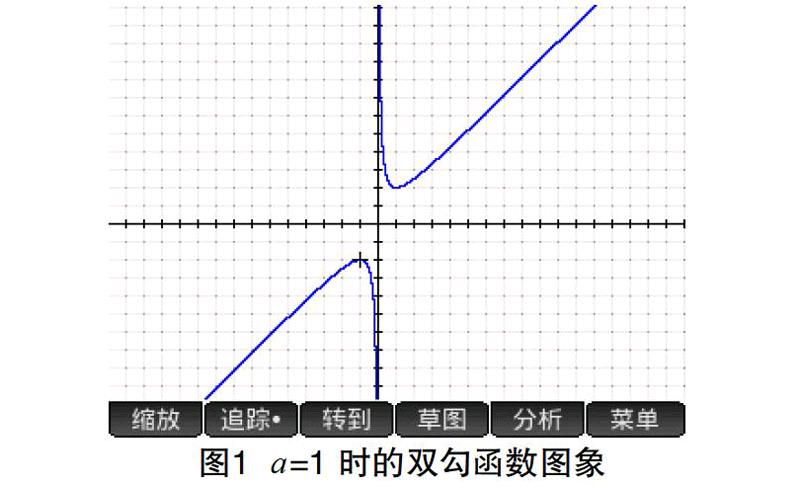
(二)本文中探究的對勾函數及其教學目標
函數可變形為其單調性本質上就是函數 的單調性的問題。因此本文探究的是函數 的單調性的教學問題。
研究對勾函數所用的最有效的工具是微積分,但學生最早接觸這類函數是在高中一年級第一個學期函數單調性的學習部分,尚不會使用導數來研究對勾函數的性質。但課程標準要求學會運用函數的圖象理解和研究函數的性質,因此基于函數單調性的定義,從對勾函數圖象的角度觀察、歸納和發現對勾函數單調性的特點,并予以證明,從而使學生更好地理解它。
二、教學過程
(一)對特例的初步操作、觀察和歸納
〖教師〗我們來研究形如 的函數(以下簡稱對勾函數)的單調性。當 a=1 時,我們用圖形計算器畫出函數 f(x)的圖象,仔細觀察圖象,并借助圖形計算器的分析功能進行分析。如圖 1 所示:
〖學生〗圖象是兩個“勾”,從圖象看,函數有 4 個單調性區間,分別是增區間、減區間、減區間和增區間。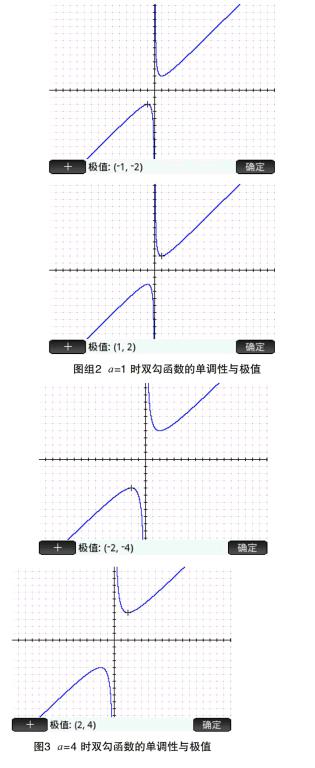
〖教師〗很好,那你能寫出具體的單調區間嗎?分析命令中的極值點功能可以幫助你找到單調區間的端點。
〖學生〗(用圖形計算器分析功能標出極值點,得到圖2),函數在(-∞,-1]遞增,在[-1,0)遞減,在(0,1]遞減,在 [1,+∞)遞增。
〖教師〗這個函數有最值嗎?如果沒有,那么函數在其定義域子區間上有最值嗎?
〖學生〗函數整體沒有最值。但是,在(-∞,0)內,當 x=-1 時函數有最大值 -2;在(0,+∞)內,當 x=1 時函數有最小值 2。
(二)對特例進一步操作、觀察和歸納
〖教師〗你們說得很對。接下來請畫出函數 的圖象,觀察圖象特點,思考它與函數 圖象的異同。
〖學生〗(作圖如圖 3)函數 在(-∞,-2]遞增,在[-2,0)遞減,在(0,2]遞減,在[2,+∞)遞增。在(-∞,0)內,當 x=-2 時函數有最大值 -4;在(0,+∞)內,當 x=2 時函數有最小值 4。
〖教師〗好,你們操作正確,結果有效。請注意函數和的異同點,再畫函數 的圖象看看,是否有類似的結論?
(三)對特例的操作、觀察、歸納和發現
〖學生〗(作圖如圖 4)結論相似。函數 在(-∞,-3]遞增,在[-3,0)遞減,在(0,3]遞減,在[3,+∞)遞增。在(-∞,0)內,當 x=-3 時函數有最大值 -6;在(0,+∞)內,當 x=3 時有最小值 6。
〖教師〗你們的想法很好,方向正確。我們考查了 a=1,4,9 的情況,對于一般的 a 呢?是否也有這樣的性質?(這是遵循從特殊到一般的思想方法)
〖學生〗應該也有。函數 在(-∞,]遞增,在[,0)遞減,在(0,]遞減,在[,+∞)遞增。在(∞-,0)內,當 時函數有最大值 ;在(0,+∞)內,當 時函數有最小值 。
〖教師〗很好,要注意,我們討論的這幾個特例都是 a>0 的情況,得到了有規律性的結論,現在,讓我們來證明這個結論。
(四)在發現中證明
〖教師〗我們以前是怎樣證明函數的單調性的?現在如何證明函數 的單調性?
〖學生〗根據函數單調性的定義,先選定一個單調區間,在選定區間上任取兩個數,比較這兩個數的函數值,進而可以證明函數在該區間上的單調性。函數 有 4 個單調區間,因此要分區間求證。
〖教師〗很好,請大家證明(學生各自進行證明)。
〖教師〗下面我們請某某同學上黑板展示他的證明過程。
學生(上講臺板書):
證明:任取兩個均不為 0 的數 x1,x2,且 x1 在區間(-∞,]內, x1-x2<0,x1x2-a>0,x1x2>0 故 f(x1)-f(x2)<0 故函數 在(-∞,]遞增。 同理可得,函數 在[,0)遞減,在(0,]遞減,在[,+∞)遞增。 〖教師〗這位同學的證明很精彩,也很簡潔。在這個證明下,“在(-∞,0)內,函數有最大值 ;在(0,+∞)內,函數有最小值 ”就是一個可以直接得到的結論。請大家回顧一下本節課的探究過程,自己總結一下有哪些收獲。 在以上教學過程中,學生利用圖形計算器經歷數學操作(圖形計算器作圖)、觀察(觀察對勾函數的圖象特點)、歸納(歸納特例的圖象特點)、發現(歸納由特殊得到一般的結論)和證明(在已有發現的基礎上進行演繹)的一系列過程,讓學生能夠自己動手“做”數學。可見,圖形計算器及類似技術具有提供驗證、啟示發現和促進理解三大功能。提出驗證指的是利用技術對某結論的若干特例進行檢驗;啟示發現指的是在技術支持下的操作、觀察、歸納和發現;促進理解則是指技術使得數學關系變得形象直觀,有助于學生捕捉到關系的本質,有助于學生對結論進行證明和應用。 【參考文獻】 [1]蔣培杰,曹 軒.高中數學實驗室的發展[J].中國教育技術裝備,2016(3) [2]劉瑞美.也談對勾函數的性質及應用[J].中學數學研究·華南師范大學版,2014(13) [3]中華人民共和國教育部.普通高中數學課程標準(實驗)[M].北京:人民教育出版社,2011 (責編 盧建龍)

