水上機場助航波能燈浮標的波能俘獲優化

王廣大 ，毛筱菲 ，2

1武漢理工大學交通學院，湖北武漢430063

2高性能艦船技術教育部重點實驗室，湖北武漢430063

水上機場助航波能燈浮標的波能俘獲優化

王廣大1，毛筱菲1，2

1武漢理工大學交通學院，湖北武漢430063

2高性能艦船技術教育部重點實驗室，湖北武漢430063

［目的］為了對水上機場波能燈浮標進行設計優化，以工作于沿海水上機場的陣列式助航波能燈浮標為研究對象，提出一種小型陣列式浮標的優化設計方法。［方法］基于三維勢流理論，計算浮標的垂蕩運動響應，在滿足最佳能量轉換部分（PTO）阻尼匹配的情況下，得到使能量俘獲寬度比最大的浮標直徑吃水比和浮標間距，然后對單個浮標的能量俘獲進行短期預報，并在此基礎上結合實際海況對陣列式浮標的能量俘獲進行長期預報，分別討論浮標直徑、吃水和浮標間距對陣列式浮標能量俘獲的影響。［結果］結果表明，當單個浮標直徑吃水比為2.4～2.6時，能量俘獲寬度比最大；陣列浮標間距越小，陣列式助航波能燈浮標的能量俘獲寬度比越大。［結論］所做的工作可為陣列式波浪能發電裝置的設計優化提供一定的參考和建議。

陣列式浮標；PTO阻尼；能量俘獲寬度比；水上機場

0 引 言

水上機場建設對于通用航空的發展有著較為重要的意義。在沿海港灣水上機場建設過程中，往往布置有一些具有指示功能的助航燈浮標，通常分布于港灣航道和機場跑道的兩側，并且浮標之間設有一定的間距，形成陣列式浮標，這類浮標往往尺度不會太大。處于海域中的燈浮標需要從海岸架設線路來輸送電力，如果將其設計成振蕩浮子式波浪能轉換裝置，則可以實現燈浮標的自發電功能以供其自身的電力需求，這對水上機場的建設，尤其是偏僻海域燈浮標的電力輸送來說具有重要意義。

振蕩浮子式波浪能轉換裝置是采用一個放在水域中的浮子來作為波浪能的吸收載體，然后將浮子吸收的能量通過能量轉換部分（Power Take-Off，PTO）轉換為電能的能源設備［1］。振蕩浮子式波能裝置具有建造難度小、效率較高等優點，適合大規模發電布置，其中陣列式布置是對振蕩浮子式波能裝置的一種有效應用。但因大規模帶來的安裝問題和發電穩定性等問題，導致目前陣列式波浪能發電裝置的應用并不多，但陣列式浮標仍然是振蕩浮子式波能裝置的研究趨勢。與單個浮子相比，陣列式布置由于浮子之間存在相互干擾，所以在進行數值模擬分析時往往需要考慮浮子間距對整體能量俘獲的影響。

國內外已有很多關于陣列式波浪能發電裝置的研究。Ringwood等［2］針對振蕩浮子式波能裝置的整個系統，用WAMIT進行裝置計算分析，包括浮子外形和PTO的配置在內，均進行了方案優化，并討論了浮子布置方式對波浪能俘獲的影響。何光宇等［3］針對一種陣列式波浪能發電裝置進行水動力分析，討論了尺度和浪向對陣列式波浪能發電裝置發電穩定性的影響。勾艷芬等［4］對簡易陣列式波浪能發電裝置進行了試驗研究，證明該裝置在沒有二次轉換的情況下仍能保證發電穩定性并提高能量轉換效率。顧煜炯等［5］針對一種陣列式波浪能發電裝置的水動力性能進行研究并開展了海上試驗，為進一步優化裝置提供了基礎。可以看到，現有的振蕩浮子式波浪能發電裝置多數是針對較深海域波浪能的俘獲和利用，有著大型化的發展趨勢且通常僅用于波能發電，而對于淺海海域，振蕩浮子式波能裝置往往應用較少，且由于淺水海域的風浪特性，裝置要求小型化的設計。目前有關小型化陣列式波浪能發電裝置的優化研究工作較少，本文將首次以工作于淺海海域的水上機場助航陣列浮標為研究對象，對燈浮標的波浪能俘獲進行優化。將浮標陣列簡化成原型為振蕩浮子式波能裝置進行波能俘獲研究。浮標通過垂蕩運動俘獲波浪能，經能量轉換裝置轉化為電能以供其自身發電。基于工程設計要求，提出一種能量俘獲的優化方法，以能量俘獲寬度比為俘獲能力的指標，分析浮標外形和浮標間距對陣列式助航波能燈浮標俘獲波浪能的影響，并對能量俘獲寬度比進行長期預報，以實現陣列式助航波能燈浮標的能量俘獲最大化，為此類陣列式波能燈浮標的進一步優化和設計以及水上機場的建設研究提供一定的參考。

1 裝置介紹

圖1所示為水上機場陣列浮標分布示意圖。根據水上機場建設要求，要求最小浮標間距為10 m，以作為燈浮標實際作業時不發生碰撞的安全距離。水上機場所處海域水深為5.5 m，并且波浪條件較為緩和；浮標為小型燈浮標，單個浮標的結構示意圖如圖2所示［6］。浮標的基本外形可視為圓柱形，通過連桿與能量轉換裝置相連并系泊于海底，采用直接驅動式發電機作為裝置的能量轉換部分，浮標在波浪中產生垂向運動，經連桿帶動發電機發電，產生的電能供自身浮標信號燈發光。

圖1 陣列浮標分布示意圖Fig.1 Arrangement of array-buoy

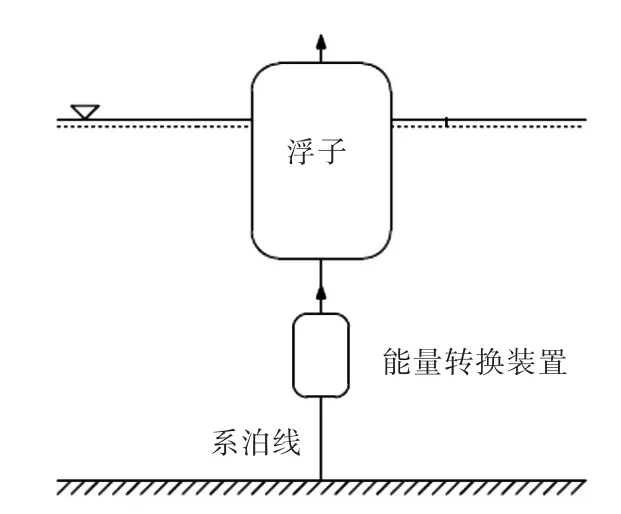
圖2 單個裝置結構示意圖Fig.2 Schematic of single wave energy converter

2 浮標運動方程

本文主要討論浮標垂向運動對波浪能的俘獲。浮標在波浪中的運動基于三維勢流理論求解，浮標的垂向運動方程為

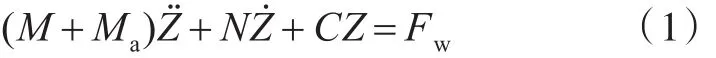
式中：Z為垂向位移；M為浮體質量；Ma為附加質量；N為阻尼系數；C為靜水恢復力項系數；Fw為波浪激勵力。

由于能量轉換部分的存在對浮標產生了作用力FPTO，由文獻［7-8］可知，當直接驅動式發電機作為波能裝置的能量轉換部分項時，僅PTO阻尼力對波浪能的轉換有貢獻，可以作為線性阻尼項處理，則能量轉換系統作用于浮標的阻尼力為

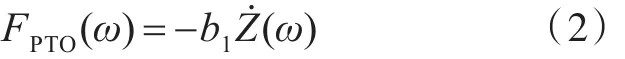
式中：b1為PTO阻尼系數；ω為頻率。

頻域內的垂蕩運動方程為

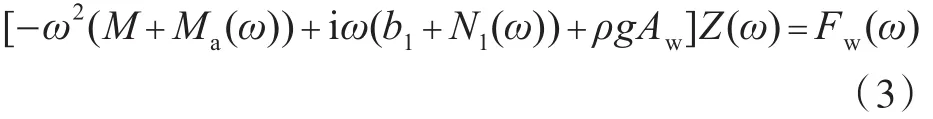
式中：N1為垂蕩阻尼系數；ρ為海水密度；g為重力加速度；Aw為浮標水線面面積。令H(ω)為浮標垂蕩運動頻率響應函數，則有

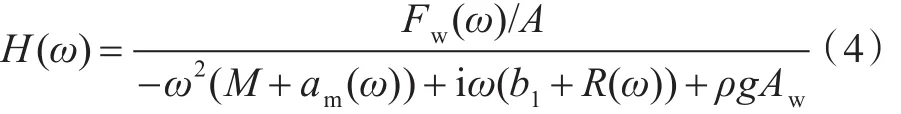
式中：A為入射波波幅；am為垂蕩附加質量；R為垂蕩固有阻尼系數。垂蕩運動頻率響應函數可由三維勢流理論計算軟件AQWA進行數值求解。

3 能量俘獲

3.1 能量俘獲寬度比

在研究陣列式波浪能發電裝置的能量俘獲能力時，引入了能量俘獲寬度比作為衡量波能裝置俘獲波浪能的指標，以對工作海域的陣列式波浪能發電裝置能量俘獲進行長期預報。能量俘獲寬度比（CWR）是描述波能裝置能量俘獲效率的重要參數，為浮標對能量的俘獲功率與浮標寬度內波浪輸入功率之比［9］：

式中：P為波浪中裝置的能量俘獲功率；Q為浮標寬度內波浪輸入的功率；D為浮標寬度，即浮標的直徑。波浪輸入功率Q是指單位時間內穿過垂直于波浪傳播方向的單位寬度截面的能量，根據線性波理論，波浪能量輸運為［9］

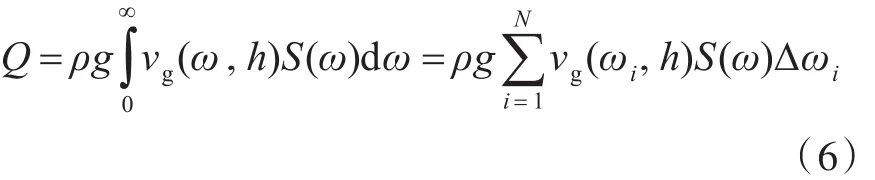
式中：vg為波群速度；S(ω)為海浪譜密度；ωi為離散求解時第i個頻率；h為水深。

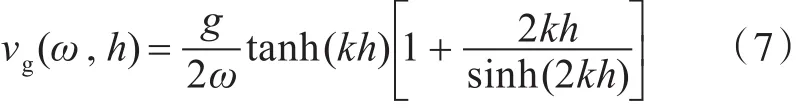
式中，k為波數。裝置的能量俘獲功率Pi為［8］

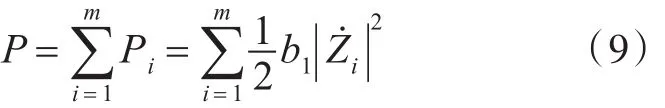
式中，m為波浪頻率總數。

3.2 最佳PTO阻尼系數

不同的PTO阻尼對應于浮標的俘獲功率也不同。由式（5）可以看出，俘獲功率與PTO阻尼系數b1成線性關系，與垂蕩運動速度呈平方關系，在求取最佳PTO阻尼系數時，可通過設置一系列的PTO阻尼系數值b1，分別代入浮標運動方程求解得到垂蕩運動速度，代入式（5）得到每個阻尼系數b1下的能量俘獲功率。對于確定尺度下的浮標，最佳PTO阻尼系數往往是一個確定值［8］。圖3給出了浮標直徑D=2.8 m，吃水d=1.5 m時能量俘獲功率隨PTO阻尼系數變化的曲線，其中曲線峰值對應的橫坐標即為最佳PTO阻尼系數，峰值對應的縱坐標則為在最佳PTO阻尼下可俘獲的最大功率。

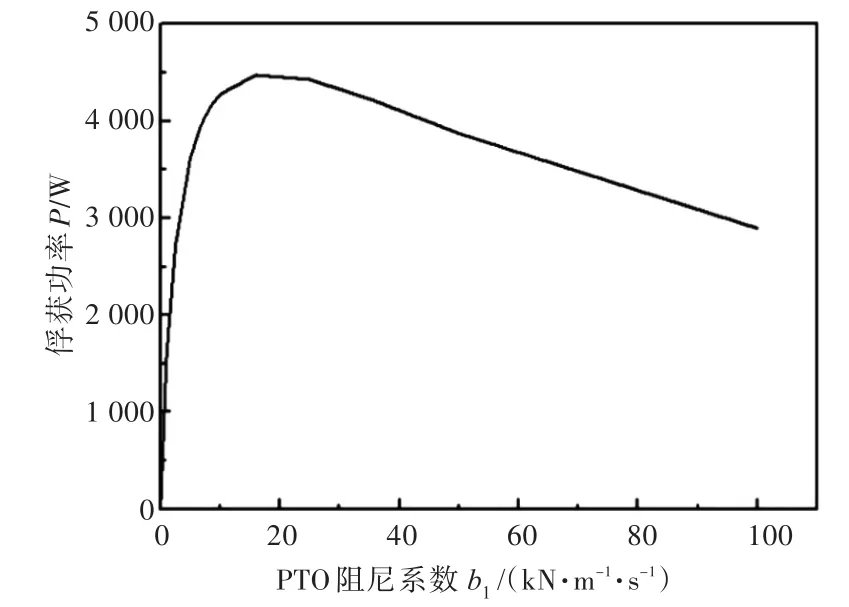
圖3 浮標俘獲功率隨PTO阻尼系數b1變化的曲線（D=2.8 m，d=1.5 m）Fig.3 Variation of power capture with respect to PTO damping coefficientb1when diameter isD=2.8 m and draft is d=1.5 m

3.3 能量俘獲的預報

陣列式浮標長期工作于海域中，要對裝置的能量俘獲進行預報，就必須對海域的長期海況進行監測和統計，結合實測海況數據或波浪散布圖等進行短期和長期預報。對于單個浮標或者陣列浮標，能量俘獲寬度比的長期預報可參照如下公式：

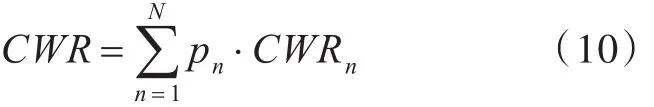
式中：pn為各海況出現的概率；CWRn為第n個海況下的能量俘獲寬度比，可由式（5）得到；N為典型海況數量。

3.4 優化流程

建立如圖4所示的陣列浮標優化流程。該方法可針對不同的海域，結合實際海域的海況條件對能量俘獲寬度比進行預報。在優化陣列浮標時，首先選擇單個浮標的外形尺度，分別計算各海況下不同尺度浮標的垂蕩運動能量俘獲寬度比，對單個浮標的能量俘獲進行短期預報，進而結合海域的波浪散布圖或其他實測波浪數據，對陣列浮標的能量俘獲進行長期預報，選出滿足工程需要的最佳尺度，包括直徑和吃水（或直徑吃水比）。

在完成單個浮標尺度優化的基礎上，對陣列式浮標進行間距調整，對陣列式浮標的總能量俘獲寬度比進行短期和長期預報，以實現能量俘獲寬度比最大化。

4 數值模擬與分析

4.1 模型參數設置

陣列浮標的排列方式為5個浮標排列。在對單個浮標的外形進行優化時，討論不同直徑吃水比（直徑吃水比D/d=1.2～6.0）下的能量俘獲寬度比，并分別討論直徑和吃水對浮標能量俘獲寬度比的影響，得到最佳尺度；在完成單個浮標外形優化的基礎上，通過分別計算各浮標間距（10～14 m）下陣列式波能發電裝置的能量俘獲寬度比，對比分析得到最佳間距值。其中，直徑吃水比的參數變化值如表1所示。

4.2 工作海域海況

工作海域的海況通常以波浪散布圖的形式來表示，需要對常年的海浪數據參數進行實時測量統計，在缺少實際海況實測資料的情況下，也可以采用海域主要成分波浪參數以及出現的概率來表示。沿海海域的波浪條件較為平穩，水上機場一般都選址在風浪較小的海域［10］。在表2所示的幾種典型海況下，分別計算裝置的能量俘獲寬度比，并結合各海況［11］出現的概率進行長期預報。

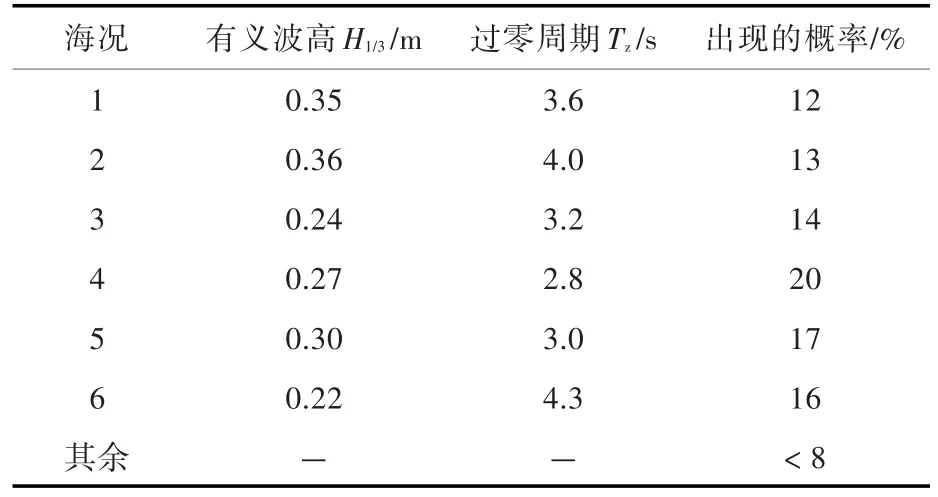
表2 工作海域海況Table 2 Sea states of work area

4.3 直徑吃水比對能量俘獲寬度比的影響

在表2所給出的海域海況下，計算各直徑吃水比下浮標裝置的能量俘獲寬度比CWR，如圖5所示。從圖中可以看出，在最佳PTO阻尼系數下，能量俘獲寬度比隨著浮標直徑吃水比的增加呈先增大后減小的趨勢，并且在直徑吃水比達2.4～2.6時能量俘獲寬度比達到最大。

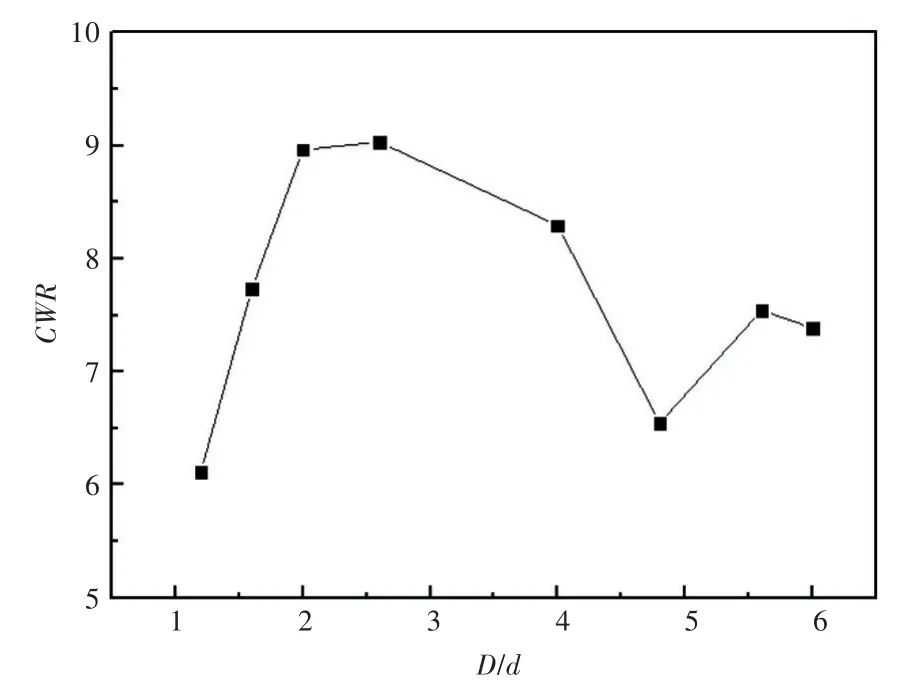
圖5 能量俘獲寬度比隨直徑吃水比變化的曲線Fig.5 Variation of energy capture width ratio with respect to diameter draft ratio

4.4 浮標直徑對能量俘獲的影響分析

為了研究浮標直徑對能量俘獲寬度比的影響，對吃水d=1 m時不同直徑下的俘獲功率P進行計算，俘獲功率隨PTO阻尼系數b1變化的曲線如圖6所示。從圖6可以看到，直徑越大的浮標對應的最佳PTO阻尼系數越大，在保證最佳PTO阻尼系數的情況下，浮標的總俘獲功率也越大。

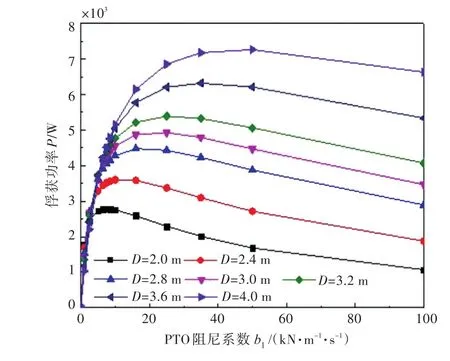
圖6 吃水為1.0 m時不同直徑尺度下俘獲功率隨阻尼系數b1的變化曲線Fig.6 Variation of power capture with respect to PTO damping coefficientb1in different diameters when draft d=1.0 m

圖7所示為在滿足最佳PTO阻尼系數的情況下，當吃水d=1 m時不同直徑浮標的能量俘獲寬度比隨外界波浪周期T的變化曲線。圖中的曲線峰值表示在該尺寸下，浮標在峰值對應的波浪周期下可以實現的最大的波浪能吸收。不同直徑的浮標，其峰值會隨直徑的減小而減小。通過對能量俘獲寬度比的短期預報可以看出，當外界波浪周期T＞3 s時，裝置的直徑尺度越大，能量俘獲寬度比越大。而在波浪周期T＜3 s時，直徑小的浮標對波浪能的俘獲要稍大一些。

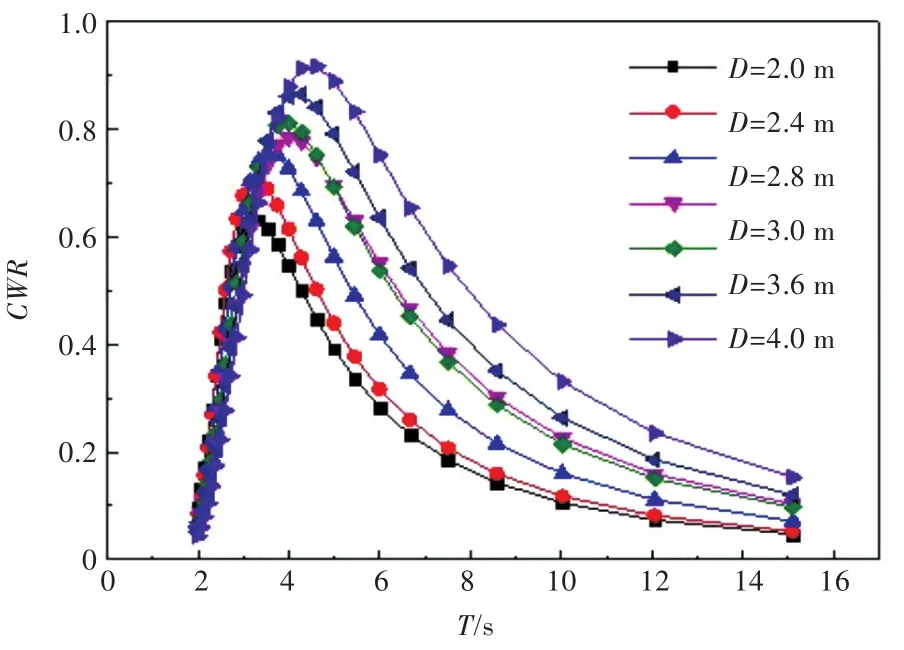
圖7 吃水為1.0 m時不同直徑尺度下能量俘獲寬度比隨外界波浪周期的變化曲線Fig.7 Variation of energy capture width ratio with respect to wave period in different diameters when draft d=1.0 m

結合圖6和圖7可以看出：對于小直徑尺度下的浮標，俘獲能量的高低主要依靠最佳PTO阻尼系數的大小，即在式（8）中，PTO阻尼系數b1占主導作用。在保證同一吃水下，直徑越大的浮標其能量俘獲效率越高。

4.5 浮標吃水對能量俘獲的影響分析

同樣，對直徑D=4 m時不同吃水下的浮標俘獲功率P進行計算。俘獲功率隨PTO阻尼系數b1變化的曲線如圖8所示。從圖8中可以看出，吃水越大的浮標對應的最佳PTO阻尼系數越小，在保證最佳PTO阻尼系數的情況下浮標總俘獲功率也越小。圖9所示為在滿足最佳PTO阻尼系數的情況下，直徑D=4 m時不同吃水浮標的能量俘獲寬度比隨外界波浪周期T的變化曲線。對于不同吃水深度的浮標，其峰值隨吃水的增加而增加。通過對能量俘獲寬度比的短期預報可以看出：當外界波浪周期T=4.2～6 s時，吃水越大，能量俘獲寬度比越大。而對于如沿海這種波浪條件較為平緩的情況（周期T＜4 s時），小吃水對能量俘獲來說反而有利。

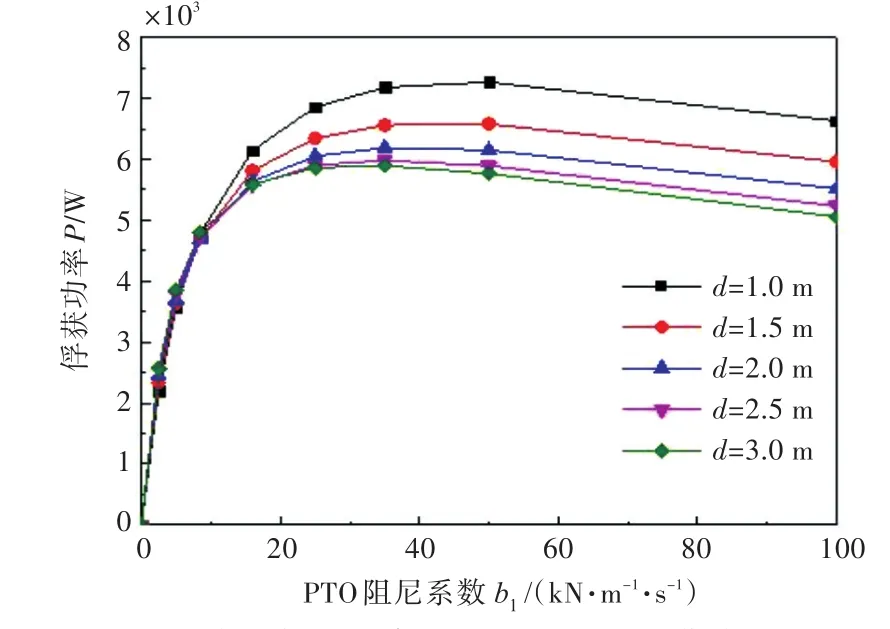
圖8 不同吃水下俘獲功率隨阻尼b1變化的曲線（D=4 m）Fig.8 Variation of power capture with respect to PTO damping coefficientb1in different drafts when diameter D=4.0 m

圖9 不同吃水下能量俘獲寬度比隨外界波浪周期變化的曲線（D=4 m）Fig.9 Variation of energy capture width ratio with respect to wave period in different drafts when diameter D=4.0 m

結合圖8和圖9可知，在外界波浪周期T＜4 s或T＞6 s的情況下，在同一直徑下，最佳PTO阻尼系數還是占據主導地位，但在外界波浪周期T＜4 s的情況下，在式（8）中，作為平方項的垂蕩速度部分影響較大。

4.6 浮標間距對能量俘獲的影響

圖10所示為陣列式波能發電裝置中的各浮標（圖1中所示浮標號）在表2所示工作海域海況條件下能量俘獲寬度比隨浮標間距的變化曲線。從中可以看出：在該海域海況條件下，3號裝置的俘獲寬度比是隨浮標間距的增加而增大；而其余浮標則是呈先下降后上升的趨勢，其中2號裝置在浮標間距為13.0 m時俘獲寬度比達到最小，1號裝置在浮標間距為12.0 m時達到最小，4號和5號裝置的俘獲寬度比在浮標間距為12～13 m時存在最小值，而最大值則均在浮標間距為10.0 m時。

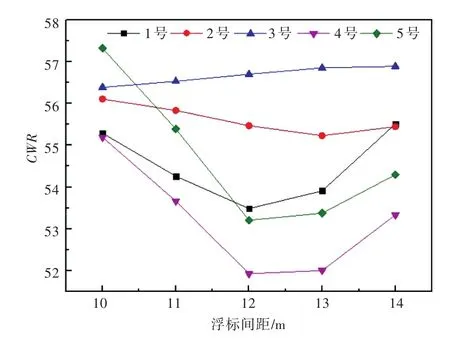
圖10 每個浮標的能量俘獲寬度比隨浮標間距的變化曲線Fig.10 Variation of energy capture width ratio of each buoy with respect to distance between array-buoy

圖11所示為陣列式浮標的總能量俘獲寬度比隨浮標間距的變化曲線。從中可以看出，在該海域海況下，隨著浮標間距的增加，陣列浮標的總能量俘獲寬度比呈先下降后上升的趨勢，且最小值出現在浮標間距為12～13 m之間。在浮標間距為10～12 m時，為了保證俘獲寬度比最大，浮標間距越小越好，即浮標間距越小，浮標之間的相互作用越明顯，對能量俘獲越有利。對能量俘獲寬度比的計算是基于表2所示工作海域的現有海況下得到的，海況條件不同，俘獲能力最高的浮標間距也不一樣。

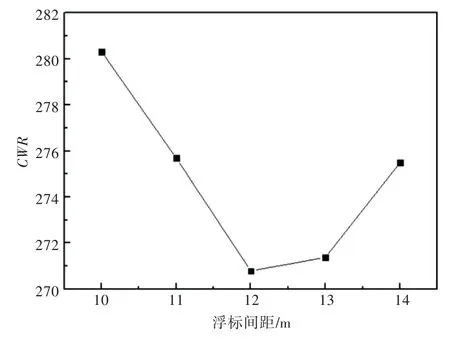
圖11 陣列式浮標的總能量俘獲寬度比隨浮標間距的變化曲線Fig.11 Variation of total energy capture width ratio of array-buoy with respect to distance between buoy

5 結 論

本文對一種應用于水上機場海域的助航波能浮標的水動力設計進行了優化，分別討論了浮標直徑和吃水以及浮標間距對浮標能量俘獲大小的影響，為陣列式波能發電裝置的設計和優化提供了參考，對水上機場建設中燈浮標設計具有一定的參考意義。文章主要得到以下結論：

1）為實現能量俘獲的最大化，浮標的最佳直徑吃水比應為在2.4～2.6之間（由于直徑和吃水會隨不同工程的要求尺寸設置不同，故本文給出的直徑吃水比在進行燈浮標設計時可以作為參考），并且在滿足水上機場建設的工程要求基礎上，陣列燈浮標間距為10 m時能量俘獲最佳。

2）對單個浮標而言，浮標的直徑越大，對應的最佳PTO阻尼系數值越大，俘獲效率越高；浮標吃水越大，對應的最佳PTO阻尼系數越小。沿海海域的波浪主要為短波，波浪周期較小，而吃水較小的浮標的能量俘獲寬度比反而更高。

3）對陣列式浮標發電裝置而言，浮標間距越小，浮標間的相互作用對垂蕩運動的影響反而較為明顯，且對能量俘獲有利。陣列式浮標用于水上機場時，在滿足工程要求的基礎上，浮標間距為10 m時陣列式浮標的能量俘獲寬度比最大。

［1］姚琦，王世明，胡海鵬.波浪能發電裝置的發展與展望［J］.海洋開發與管理，2016，33（1）：86-92.YAO Q，WANG S M，HU H P.On the development and prospect of wave energy power generation device［J］.Ocean Development and Management，2016，33（1）：86-92（in Chinese）.

［2］RINGWOOD J V，BACELLI G，FUSCO F.Control，forecasting and optimisation for wave energy conversion［J］.IFAC Proceedings Volumes，2014，47（3）：7678-7689.

［3］何光宇，楊紹輝，何宏舟，等.陣列式波浪能發電裝置的水動力分析［J］.水力發電學報，2015，34（2）：118-124.HE G Y，YANG S H，HE H Z，et al.Hydrodynamic analysis of array-type device of wave energy generation［J］.Journal of Hydroelectric Engineering，2015，34（2）：118-124（in Chinese）.

［4］勾艷芬，葉家瑋，李峰.陣列振蕩浮子式波能轉換裝置試驗［J］.廣東造船，2007（2）：1-3.GOU Y F，YE J W，LI F.Investigation on the array os?cillating buoy wave power device［J］.Guangdong Ship?building，2007（2）：1-3（in Chinese）.

［5］顧煜炯，謝典，耿直.陣列浮子式波浪能發電裝置的水動力性能分析［J］.水力發電學報，2016，35（8）：114-120.GU Y J，XIE D，GENG Z.Hydrodynamic analysis of wave power generation devices of array buoy type［J］.Journal of Hydroelectric Engineering，2016，35（8）：114-120（in Chinese）.

［6］ BABARIT A，HALS J，MULIAWAN M J，et al.Numeri?cal benchmarking study of a selection of wave energy converters［J］.Renewable Energy，2012，41：44-63.

［7］OSKAMP J A，?ZKAN-HALLER H T.Power calcula?tions for a passively tuned point absorber wave energy converter on the Oregon coast［J］.Renewable Energy，2012，45：72-77.

［8］ GOGGINS J，FINNEGAN W.Shape optimisation of floating wave energy converters for a specified wave en?ergy spectrum［J］.Renewable Energy，2014，71：208-220.

［9］程正順，楊建民，胡志強，等.直接驅動浮子式波浪能轉換裝置頻域模擬研究［J］.太陽能學報，2014，35（7）：1304-1310.CHENG Z S，YANG J M，HU Z Q，et al.Frequency do?main modeling and analysis of a direct drive point ab?sorber wave energy converter［J］.Acta Energiae Solaris Sinica，2014，35（7）：1304-1310（in Chinese）.

［10］郭曉平，葛春景.關于水上機場建設有關問題的探討［J］.中國民用航空，2015（12）：50-51.GUO X P，GE C J.The discussion on seadrome con?struction［J］.China Civil Aviation，2015（12）：50-51（in Chinese）.

［11］周宇英，李炳強，蔡宗舉，等.陀螺式波浪能發電裝置浮子運動及載荷分析［J］.船海工程，2016，45（3）：90-98.ZHOU Y Y，LI B Q，CAI Z J，et al.Study on motion and load of the floater in top-shaped wave power gen?eration device［J］.Shipamp;Ocean Engineering，2016，45（3）：90-98（in Chinese）.

Optimization of wave energy capture of wave-powered navigational lighting buoys of seadromes

WANG Guangda1，MAO Xiaofei1，2
1 School of Transportation，Wuhan University of Technology，Wuhan 430063，China
2 Key Laboratory of High Performance Ship Technology of Ministry of Education，Wuhan 430063，China

［Objectives］This paper proposes an optimized design for wave-power navigational lighting buoys of seadromes.［Methods］Based on the theory of three-dimensional potential flow，the buoyant motion response of a buoy is calculated.A type of array of wave-power navigational lighting buoys located in an offshore seadrome is proposed，and a procedure for the design optimization of its component buoys is presented.Matching the best Power Take-Off（PTO） damping，the diameter to draft ratio and array distance with the best energy capture width ratio are acquired，and the energy capture for the short-term forecast of the buoy array is accomplished.On this basis，combined with the actual sea conditions，energy capture for the long-term forecast of an individual buoy is accomplished.The influence of the buoy diameter，buoy draft and array distance on the energy capture width ratio is discussed.［Results］The results show that the energy capture width ratio is at its greatest when the diameter to draft ratio is between 2.4-2.6；the smaller the distance between array buoys，the greater the energy capture width of each buoy.［Conclusions］The results can provide a reference and suggestions for the optimization of the design of wave energy generation for arrays buoy.

array buoy ；PTO damping；energy capture width ratio；seadrome

P743.2

A

10.3969/j.issn.1673-3185.2017.06.003

http://kns.cnki.net/kcms/detail/42.1755.TJ.20171128.1112.026.html期刊網址：www.ship-research.com

王廣大，毛筱菲.水上機場助航波能燈浮標的波能俘獲優化［J］.中國艦船研究，2017，12（6）：15-21.

WANG G D，MAO X F.Optimization of wave energy capture of wave-powered navigational lighting buoys of seadromes［J］.Chinese Journal of Ship Research，2017，12（6）：15-21.

2017-05-11 < class="emphasis_bold"> 網絡出版時間：

時間：2017-11-28 11:12

國家科技支撐計劃課題（2014BAC01B02）

王廣大，男，1992年生，碩士生。研究方向：船舶與海洋工程水動力性能。

E-mail：1014119127@qq.com

毛筱菲（通信作者），女，1962年生，教授。研究方向：船舶與海洋工程水動力性能